基于导弹预警功能建模的预警参数分析

郭 旭，陆 港，周 潇

(空军预警学院，湖北 武汉 430019)

0 引 言

弹道导弹预警是战略反导作战的前提，其发展水平关乎国家命脉，因而受到了广泛重视。由于起步较早，国外军事强国的预警体系建设已较为完善，具备了很强的预警探测能力[1-2]。要对导弹的预警过程及预警参数进行分析，需要使用多种专业功能突出的仿真软件[3]。其中STK功能强大，可用于航天、情报、雷达、电子对抗、导弹防御等各方面[4-5]。我国目前已经开始弹道导弹预警体系的开发，但由于起步较晚，很多技术尚处于起步阶段，还需要很多探索。

探索研究预警参数与导弹各项预警参数之间的关系，从而找到最合理的优化配置方法，选择合理的探测精度，得到最为优化的预警结果，在一定程度上可以提高导弹预警系统的总体设计质量，为今后导弹仿真优化设计以及对我国的弹道预警体系提供参考。

1 导弹落点预报及误差分析

通过卫星观测导弹，并将信息提供给雷达，雷达就能对目标导弹进行观测，得到目标导弹在一段时间内的位置、速度信息。根据这些信息，就可以对目标导弹的落点进行预报。

1.1 航天器坐标系简单介绍

为了描述运动点的规律，确定点在空间中的位置，必须确定恰当的坐标系，包括确定坐标原点、参考平面和参考平面上的主方向3个要素。这里首先对常用的坐标系进行以下简单介绍：

(1) 地心惯性坐标系OeXIYIZI

地心惯性坐标系是一个惯性参考基准，用来描述航天器在惯性空间中的绝对运动。地心惯性坐标系OeXIYIZI的3个要素定义如下：

(a) 坐标原点为地球质心。

(b) 参考平面OeXIYI为地球赤道面。

(c) 参考平面上的主方向：OeXI轴指向春分点方向；OeZI轴与地球南北轴重合，指向北极；OeYI轴与OeXI轴和OeZI轴构成右手坐标系。

(2) 地心固连坐标系OeXEYEZE

地心固连坐标系是随地球一同转动的动参考基准，用以描述航天器相对地球的视运动，即航天器相对地球的相对运动。地心固连坐标系OeXEYEZE的3个要素定义如下：

(a) 坐标原点Oe为地球质心。

(b) 参考平面OeXEYE为地球赤道面。

(c) 参考平面上的主方向：OeXE轴在赤道面指向格林尼治子午线(零子午线)方向；OeZE轴与地球南北轴重合，指向北极；OeYE轴与OeZE轴构成右手坐标系。

(3) 导弹发射极坐标系o1x1y1z1

导弹极坐标系是以导弹的发射点为参考点，用来描述导弹相对与发射点的视运动。导弹极坐标系o1x1y1z1的3个要素定义如下：

(a) 坐标原点o1为导弹在地球表面的发射点。

(b) 参考平面为与发射点所在位置相切的平面。

(c) 参考平面上的主方向：o1y1指向导弹的发射方向；o1x1与o1z1构成右手坐标系。

(4) 瞬时地心坐标系oxyz

瞬时地心坐标系也称为真地球坐标系，它的3个要素定义如下：

(a) 坐标原点位于地球质心。

(b) 参考平面OeXEYE为地球赤道面。

(c) 参考平面上的主方向：oz轴指向瞬时地球自转轴方向，ox轴指向瞬时赤道面和包含瞬时地球自转轴与平均天文台参考点的子午面的交点。

(5) J2000惯性坐标系oAxAyAzA

由于恒星赤经和赤纬会因岁差(与恒星的自行)改变，所以天文学家们经常指定某一特定的纪元作参考点。J2000坐标系是指由J2000时刻的天赤道与二分点来定义天球参考坐标系。它是在天文学上使用的历元，前缀“J”代表这是一个儒略纪元法，它指的是儒略日期TT时2 451 545.0，即相对于世界协调时间2000年1月1日11∶58∶55.816。

1.2 常见坐标系之间的转换

1.2.1 地心惯性坐标系、地心固连坐标系之间的转换

航天器在地心惯性坐标系OeXIYIZI和地心固连坐标系OeXEYEZE的三维位置表示是不相同的，但可以相互转换。2种坐标系的原点以及OeZI轴与OeZE轴始终是重合的，地心固连坐标系OeXE轴和OeYE轴却始终绕地球南北轴转动，而地心惯性坐标系在惯性空间中固定不动。如果知道某初始时刻t0地心固连坐标系的OeXE和地心惯性坐标系OeXI轴之间的夹角θ=θ0+Ωe(t-t0)，Ωe为地球自转速度，其值约为7.292 115 ×10-5rad/s。

设在t0时刻之后的任意时刻t，航天器在地心惯性坐标系和地心固连坐标系中的三维位置用直角坐标表示分别为(xI,yI,zI) 和(xE,yE,zE)，两者之间可以采用下式进行相互转换，即：

(1)

式中：θ为此时刻地心固连坐标系的OeXE轴与地心惯性坐标系的OeXI轴之间的夹角。

1.2.2 地心固连坐标系OeXEYEZE与极坐标o1x1y1z1的转换

极坐标系转换到地心固连坐标系，可以先把极坐标系o1x1y1z1转换到地心惯性坐标系OeXIYIZI，然后再把地心惯性坐标系OeXIYIZI转换成地心固连坐标系OeXEYEZE。

1.3 导弹落点预报算法

1.3.1 将雷达探测到的导弹数据进行坐标系转换

(1) 导弹极坐标系o1x1y1z1转换到导弹发射坐标系oxyz

利用STK生成的导弹弹道选择2个时刻TQ和TP，记录2个时刻下对应的雷达测量的导弹参数[6](方位角αQ、αP,俯仰角βQ、βP,径向距离rQ、rP)，这实际上相当于导弹在发射极坐标系下的坐标(αQ,βQ,rQ)、(αP,βP,rP)。

通过坐标系转换，可以得到导弹在发射坐标系oxyz下的坐标(xQ,yQ,zQ)、(xP,yP,zP)。坐标系转换过程如下：xQ=rQcosβQcosαQ,yQ=rQsinβQ,zQ=rQcosβQsinαQ;xP=rPcosβPsinαP,yP=rPsinβP,zP=rPcosβPsinαP。

(2) 导弹发射坐标系oxyz转换到地心坐标系OeXEYEZE

得到导弹在发射坐标系oxyz下的2点的坐标(xQ,yQ,zQ)及(xP,yP,zP)后，继续进行坐标系转化，得到这2点在地心坐标系OeXEYEZE下的坐标。这2个坐标系的转化方法如下：

这里已知雷达地理坐标(λ0,φ0,h)，其中λ0是雷达方位角，φ0是雷达的俯仰角，h是雷达的高度。坐标系的关系如图1所示。

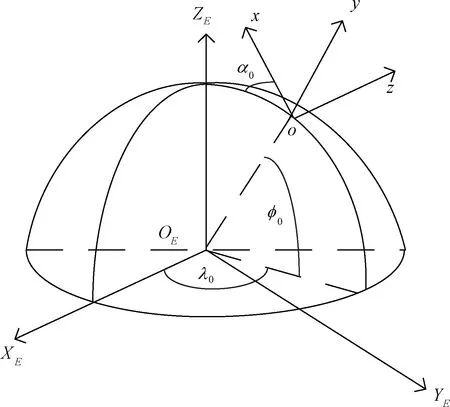
图1 坐标系转换示意图

根据图1，可以得到2个坐标系之间的转化关系：

(2)

GE=M2[-(90°+α0)]M1[φ0]M3[λ0-90°]

(3)

这样就得到了导弹在地心坐标系下的坐标。

(3) 地心惯性坐标系OeXIYIZI转换成地心固连坐标系OeXEYEZE

将地心坐标系下的坐标(XE,YE,ZE)转换到发射瞬时地心坐标系下(XI,YI,ZI)，坐标转化公式为：

(4)

IE=M2[ΩG+we·t]·M3[ΩG]

(5)

这样就得到了导弹在发射瞬时坐标系下的坐标。

最终要将发射瞬时地心坐标系下的坐标(XI,YI,ZI)转换到地心惯性坐标系J2000下(XJ,YJ,ZJ)，转换过程需考虑地球自转与摄动的影响。

1.3.2 弹道导弹落点预报算法

首先以弹道所在平面为坐标平面，以地球球心O(椭圆轨道1个焦点)为坐标原点，以长轴所在直线为Yd轴建立弹道平面坐标系，P、Q两点为导弹飞行过程中的两点，B为导弹落点，如图2所示。

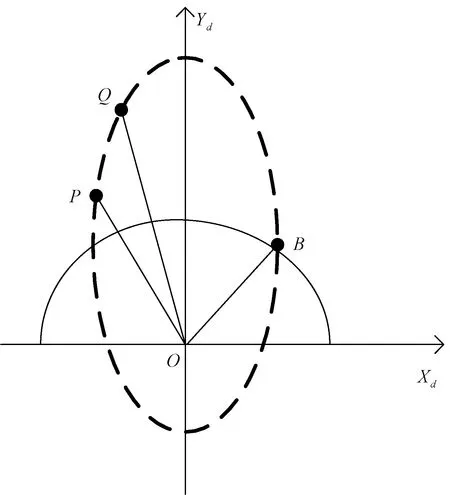
图2 导弹飞行模型

根据STK直接读出P、Q两点的vP,vQ及rP,rQ，计算相关轨道根数和P、Q点坐标，计算步骤如下：

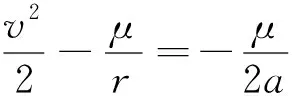
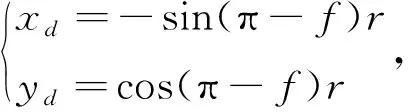
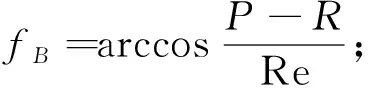
计算导弹在J2000坐标系下落点时，利用线性空间内积不变原理：

(6)

上式可简化为：

(7)

将对应的坐标代入，会发现上式是一个关于(x1,y1,z1)的三元二次方程，求解即可得到导弹在J2000坐标系下的落点坐标(x1,y1,z1)。

2 导弹飞行时间的计算及误差分析

2.1 导弹飞行时间的计算模型

首先以弹道所在平面为坐标平面，以地球球心O(椭圆轨道一个焦点)为坐标原点，以长轴所在直线为Yd轴建立弹道平面坐标系，Xd轴为与Yd轴垂直的坐标轴。A为导弹发射点，B为导弹弹着点，如图3所示。

图3 导弹飞行时间计算模型

根据STK直接读出B点的vB及rB，计算B点对应的真近点角，计算过程如下：

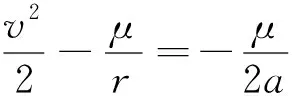
2.2 导弹飞行时间算法的稳定性及有效性仿真分析

以上是在理想状况下，之后对vP,vQ及rP,rQ分别引入均值为0的高斯白噪声。进行100次独立重复试验，计算出每次试验对应的落点,预报平均值和均方根误差，并画出对应曲线。

2.2.1 仿真分析流程

图4 导弹飞行时间算法流程图

导弹飞行时间算法的稳定性仿真验证步骤如图4所示,主要包括以下步骤：

(1) 利用STK进行雷达探测导弹仿真，得到导弹在飞行过程中每一时刻的位置、速度信息。

(2) 通过坐标系转换，将导弹在极坐标系下的位置信息转化到J2000坐标系下。

(3) 调用向量内积不变算法，进行导弹落点预报。

(4) 在雷达的探测数据中引入测量误差，并在不同测量误差等级下进行多次独立重复试验，求得各噪声等级下落点预报均值和均方根误差。

(5) 绘制曲线图。

(6) 分析落点预报算法对于测量误差的稳定性。

2.2.2 对导弹的位置测量数据加入误差，验证算法

首先在导弹的位置测量信息中加入均值为0、方差为σ=0∶50∶500的高斯白噪声，进行100次独立重复试验，计算出每次试验对应的落点预报平均值和均方根误差，并画出对应曲线，结果如图5所示。

图5 加入速度测量误差后的导弹飞行时间预测效果图

通过图6可以看出，加入均值u=0、方差为σ=0∶50∶500(单位m)的位置测量误差后，导弹预测飞行时间的均值比较稳定，变化不大，说明飞行时间的预测值对位置测量的稳定性较好。

图6 加入速度测量误差后的导弹飞行时间均值

通过图7可以看出，导弹预测飞行时间的均方根误差(RMSE)并未随着误差等级σ的增大而增大，稳定在5 s附近，整体波动幅度较小，说明位置测量误差对导弹飞行时间的预测影响较小。对于导弹飞行时间的预测，实际应用中可以放宽对导弹位置测量精度的要求。

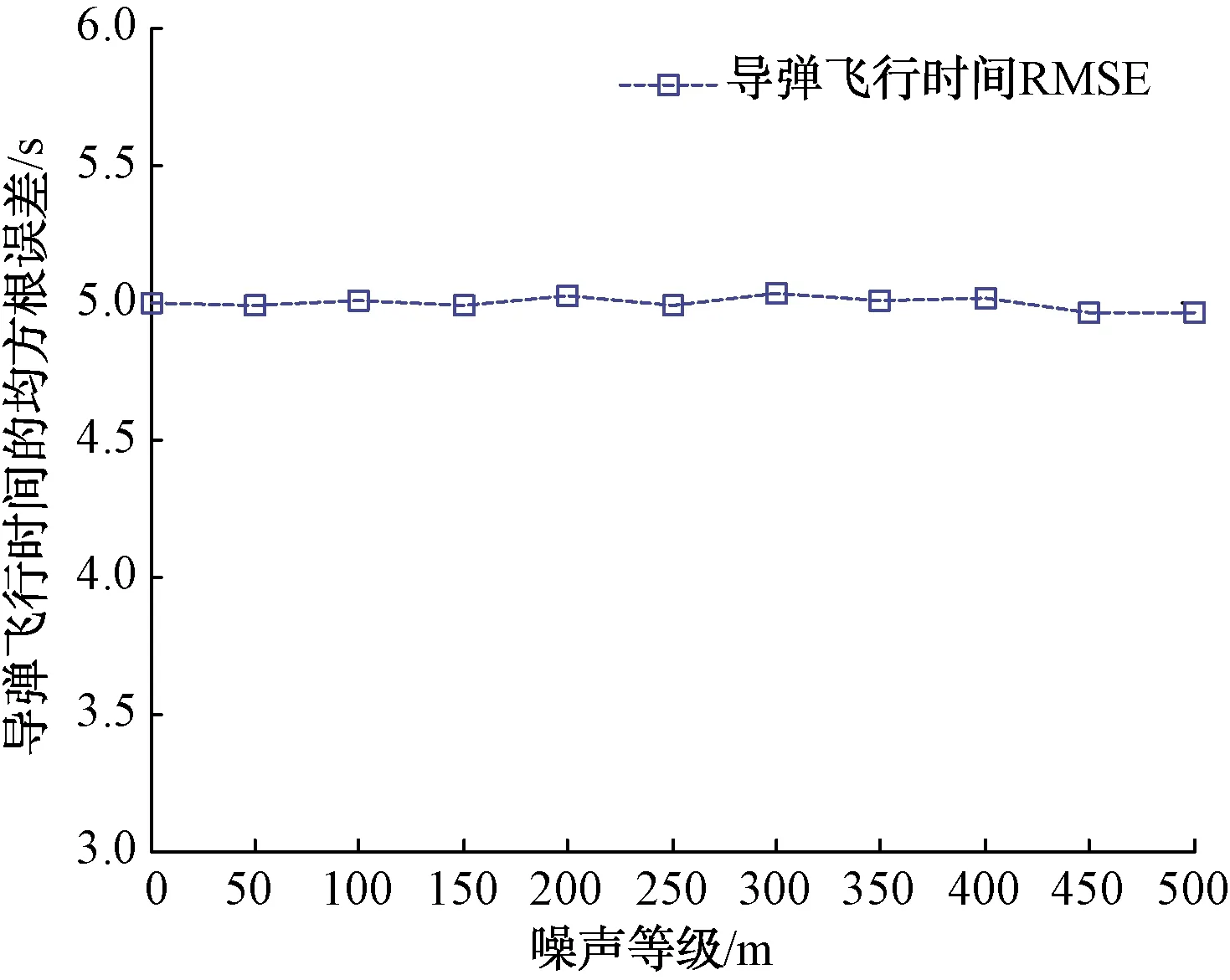
图7 加入速度测量误差后的导弹飞行时间RMSE

2.2.3 对导弹的速度测量数据加入误差，验证算法

在导弹的速度测量信息中引入均值为0、方差为0∶50∶500的高斯白噪声，同样进行100次独立重复试验，计算出每次试验对应的落点预报平均值和均方根误差，并画出对应曲线，结果如图8所示。

图8 软件进行导弹飞行时间预测的效果图

通过图9可以看出，加入均值u=0、方差为σ=0∶50∶500 m/s的速度测量误差后，导弹预测飞行的均值稳定在1 810 s附近，有小范围的变化。即使速度测量误差的均值u=0，但导弹预测落点均值曲线不是一条直线，而是一条曲线，这说明导弹速度测量误差对于飞行时间的预测有一定影响。

图9 加入速度误差后的导弹飞行时间均值

通过图10可以看出，导弹预测飞行时间的RMSE随着测量误差的增大而增大，并且增速较快。

与图7相比，仅在速度测量误差σ=50 m/s时，导弹预测落点的RMSE就已达到34.096 6 s；而当测量误差σ=500 m/s时，导弹预测落点的RMSE将达到347.204 4 s。这说明导弹速度测量误差对最终的导弹飞行时间预报精度影响较大，在实际应用中，应尽可能地控制速度测量误差，使其位于较小的范围内。

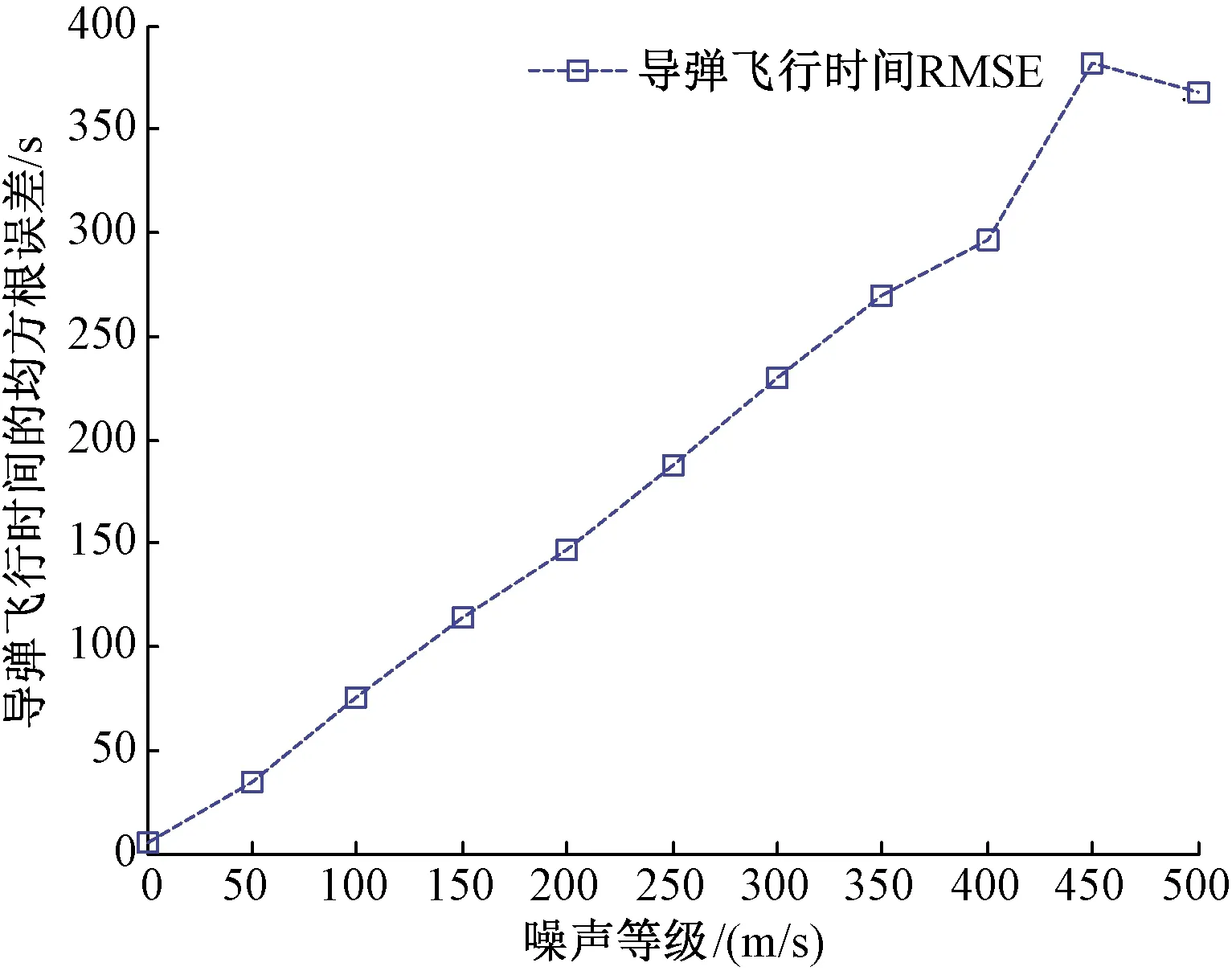
图10 加入速度误差后的导弹飞行时间RMSE

2.3 落点预报算法稳定性仿真分析

2.3.1 仿真分析流程

导弹落点预报算法的仿真验证步骤如图11所示[7]。

图11 导弹落点预报算法流程

主要步骤如下：

(1) 利用STK进行雷达探测导弹仿真，得到导弹在飞行过程中每一时刻的位置、速度信息。

通过坐标系转换，将导弹在极坐标系下的位置信息转化到J2000坐标系下。

调用向量内积不变算法，进行导弹落点预报。

(2) 在雷达的探测数据中引入测量误差，并在不同测量误差等级下进行多次独立重复试验，求得各噪声等级下落点预报均值和均方根误差。

(3) 绘制曲线图。

(4) 分析落点预报算法对于测量误差的稳定性。

2.3.2 对导弹的位置测量数据加入误差，验证算法

验证算法稳定性的步骤为：

首先用VC调用STK建立场景[8-9]，场景的起始时刻为“2007年7月1日12∶00”，结束时刻为“2007年7月2日12∶00”。

随后建立导弹与雷达坐标系。这里选择更贴合实际的仿真场景，由于印度始终是我国在西南方向的一个有力对手，其最新研制的“烈火-5”型弹道导弹的打击范围已经可以覆盖北京。

因此假设导弹的发射点位于印度的新德里，其经纬度、海拔为(78.10°，13.37°，0 km)，弹着点假设

位于我国北京，其经纬度、海拔为(116°,39.9°，0 km)。监测雷达位于云南，其经纬度、海拔为(103.34°，34.15°，2 km)。至此场景参数设定完毕。利用雷达监测导弹，得到来袭导弹在不同时刻的位置、速度信息。通过这些数据，调用落点预报算法，就可以进行导弹落点预报。

最后，在雷达所监测到的导弹位置信息中分别引入均值为0、方差为0∶50∶500的高斯白噪声，进行100次独立重复试验，计算出每次试验对应的预测落点平均值和均方根误差，并画出对应曲线，计算结果如图12～图14所示。

图12 加入位置测量误差后导弹落点预报的效果图

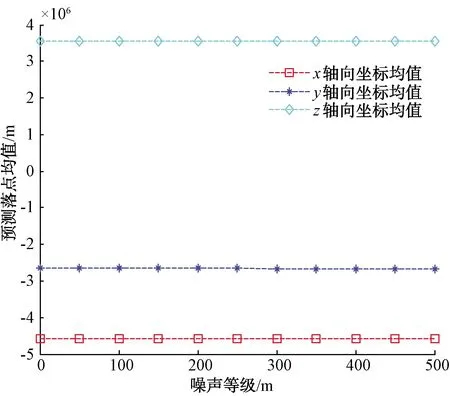
图13 加入位置测量误差后的导弹预测落点均值

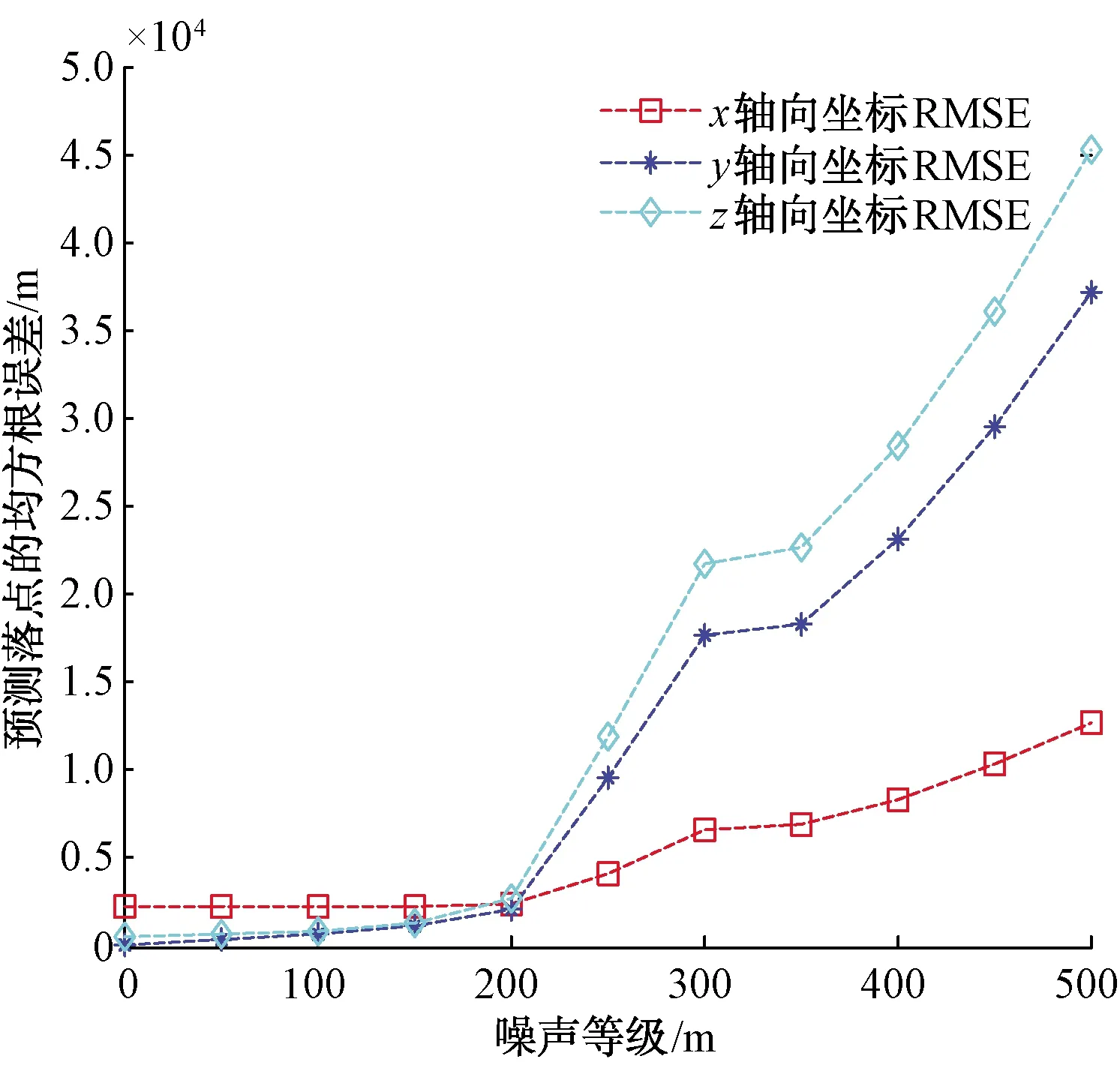
图14 加入位置测量误差后预测导弹预测落点的RMSE

通过图13可以看出，加入均值u=0、方差为σ=0∶50∶500(单位m)的位置测量误差后，导弹预测落点的均值比较稳定，变化不大，说明导弹预测落点均值对位置测量的稳定性较好。

通过图14可以看出，在位置测量误差σ<150 m时，导弹预测落点的RMSE位于0.043～6.3 km范围内，比较稳定。并且由正态分布的特性可知，当位置测量误差σ>150 m时，导弹预测落点的RMSE将随着测量误差的增大而骤然增大，说明当测量误差大于某一等级后，落点预测算法的稳定性开始降低，将无法满足落点预测精度。因此应该将位置测量误差σ控制在150 m以内。

2.3.3 对导弹的速度测量数据加入误差，验证算法

在得到的导弹在不同时刻的速度信息中引入均值为0、方差为0∶50∶500的高斯白噪声，同样进行100次独立重复试验，计算出每次试验对应的落点预报平均值和均方根误差，并画出对应曲线，结果如图15～图17所示。

图15 加入速度测量误差后的导弹落点预报效果示意图

图16 加入速度测量误差后的导弹预测落点均值

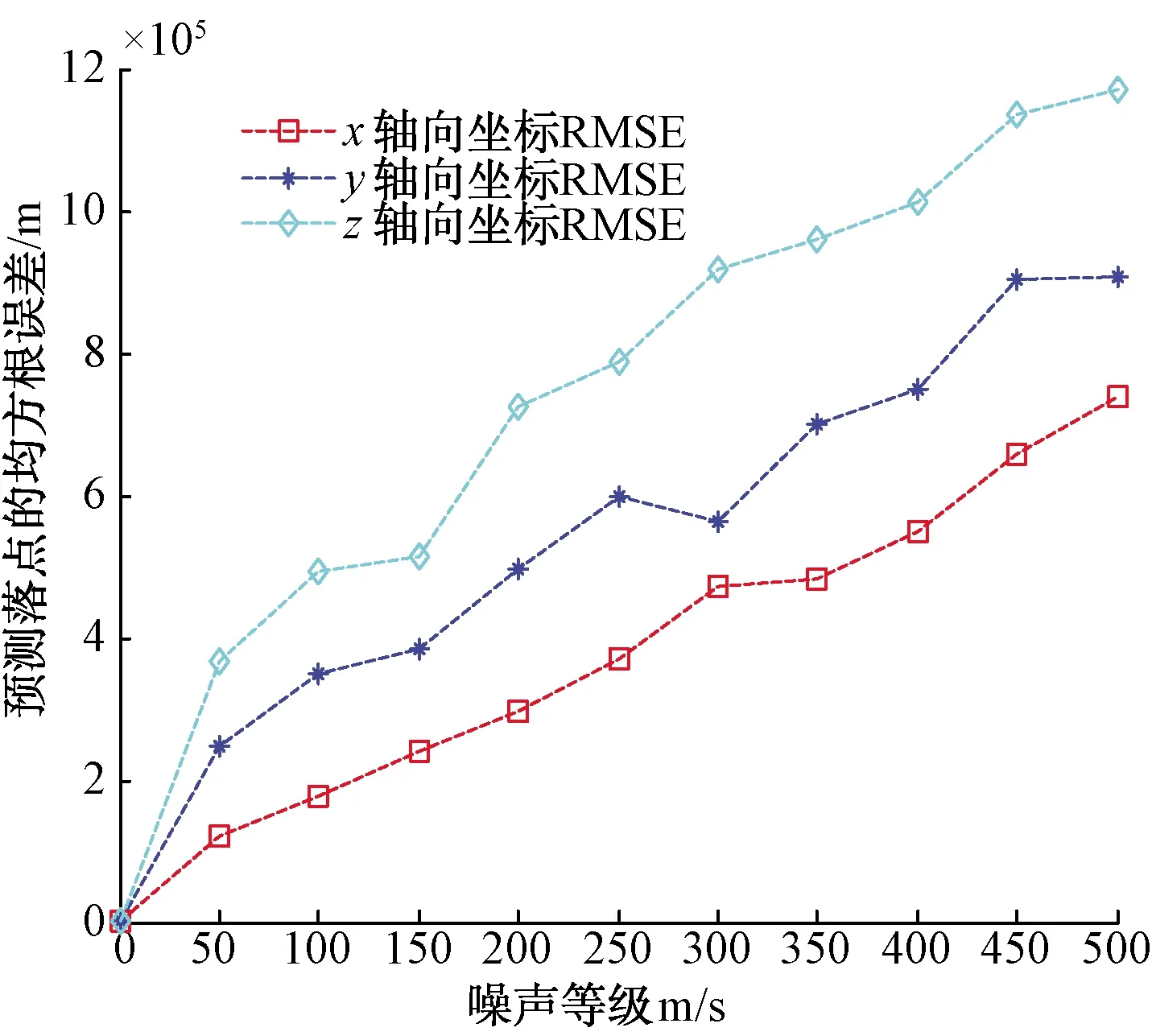
图17 加入速度测量后的导弹预测落点RMSE

通过图16可以看出，加入均值u=0、方差为σ=0∶50∶500(单位m/s)的速度测量误差后，导弹预测落点的均值有小范围的变化，说明导弹的落点预测与测量速度有一定的关系，即使速度测量误差的均值u=0，但导弹预测落点均值曲线不是一条直线，而是一条曲线。

通过图17可以看出，导弹预测落点的RMSE随着测量误差的增大而增大，并且增速较快。与图14相比，仅在速度测量误差σ=50 m/s时，导弹预测落点的RMSE就已超过10 km，而当测量误差σ=500 m/s时，导弹预测落点的RMSE将达到126.10 km。说明导弹速度测量误差对最终的导弹落点预报精度影响较大，在实际应用中，我们应该尽可能地控制速度测量误差，使其位于一个较小的范围内。

3 结束语

介绍了导弹的预警参数中的弹着点位置及飞行时间这2个参数的计算模型。对于弹着点进行求解计算，本文采用的是线性空间不变法。这种算法，相较于传统的解析式法来说，计算量小，运算速度块，实时性好；在导弹的飞行时间计算方面，本文采用的是椭圆轨道的交点法；在介绍了导弹的预警参数的计算模型之后，本文又对这种算法的稳定性及有效性进行了分析。

通过分析得到了不同类别的测量误差对导弹预警参数预报精度的影响程度。在计算资源有限的情况下，优先保证对预报精度影响较大的误差的测量精度，从而能够对现有的预警过程进行优化，提高导弹预警的准确性。