机载双站对地面辐射源时差定位误差分析
2020-08-26周伟江
张 磊,周伟江
(1.中国船舶重工集团公司第七二三研究所,江苏 扬州 225101;2.航天工程大学,北京 101416)
0 引 言
按照观测站对辐射源目标接收的信号参数不同,无源定位技术主要包括多站时差定位技术、双站测向交叉定位技术、时差和频差相结合定位技术以及时差和测向相结合的定位技术等[1-8]。针对空中机载平台对地面辐射源定位的应用场景,多站时差定位精度较高,但是一般至少需要3个观测站,同时对多站之间的时间同步精度要求高;双站测向交叉定位精度受限于双站基线长度和测角精度,在实际应用过程中,当目标距离观测平台较远时(超出几倍基线长度),对辐射源的定位精度较差甚至无法对辐射源进行定位;多普勒频差定位精度比较低,并且在对三维空间中的目标进行定位时,一般需要至少3个观测站,同时目标与观测平台之间需要有相对运动,观测平台的布站方式对定位精度有较大的影响。双站测向时差定位是联合观测平台测得的方位信息与到达时间差信息,具有定位精度高、结构简单等特点[9-18]。
目前,基于测向时差体制的无源定位主要应用于地面固定观测平台,而对应用于空中机载平台的测向时差无源定位技术研究较少。文献[19]提出了一种基于舰载平台的多站联合测向时差定位系统,文献[20]介绍了一种基于地面固定双站测向时差定位系统。因此,针对空中机载平台对地面目标的定位场景,本文建立了基于机载平台的双站测向时差定位模型,并对双站的基线长度、测向时差误差、测角误差以及机载平台本身的姿态信息对定位精度的影响进行了仿真分析研究。
1 基于空中机载观测平台的双站测向时差定位模型
基于空中机载观测平台的双站测向时差定位模型示意图如图1所示。

图1 基于空中机载观测平台的双站测向时差定位模型
如图1所示,以观测主平台的质心为原点建立坐标系,观测主站的坐标为(x1,y1,z1),辅站的坐标为(x2,y2,z2),辐射源目标的坐标为(x,y,z)。r1为观测主站到辐射源目标的距离,r2为观测辅站到辐射源目标的距离,α为观测主站相对于辐射源目标的方位角,β为观测主站相对于辐射源目标的俯仰角,观测平台主站和辅站测得的辐射源到达时间差为Δt。
根据图1可得:
(1)
(2)
r12=(x-x1)2+(y-y1)2+(z-z1)2
(3)
r22=(x-x2)2+(y-y2)2+(z-z2)2
(4)
Δt2c2=(r1-r2)2
(5)
以观测平台主站质心为原点的坐标系中,设观测平台主站的坐标为(0,0,0),则有:
r22-r12=x22+y22+z22-
2(x2·x+y2·y+z2·z)
(6)
联合公式(1)~(4),可以得到:
x=r1cosβcosα
(7)
y=r1cosβsinα
(8)
z=r1sinβ
(9)
将公式(7)、(8)、(9)代入公式(6)中,可以得到:
r1=
(10)
上述计算方式是以观测平台主站为原点的坐标系,文献[21]和文献[22]给出了机载平台坐标系与大地直角坐标系的坐标转换矩阵,从而实现基于机载平台的测向时差定位解算过程中引入观测机载平台的姿态信息。
假设辐射源目标大地直角坐标系下的坐标为(X,Y,Z),观测平台主站和辅站在大地直角坐标系下的坐标为(X1,Y1,Z1)和(X2,Y2,Z2),机载坐标系与大地直角坐标系的位置转换如下:
(11)
式中:Q2为机载坐标系与大地直角坐标系的转换矩阵;Q1为大地直角坐标系与大地坐标系的转换矩阵[21],其可表示为:
(12)
(13)
式中:θa,θb和θc分别为机载平台的横滚角、航向角和俯仰角;B0和L0分别为大地坐标系中位置点的经度和纬度。
将公式(11)代入公式(10)中,就可以得到在大地直角坐标系下目标距离信息,另外,大地直角坐标系下的目标位置坐标可以用下式表示[21]:
(14)
基于机载平台的双站测向时差定位精度可表示为:
(15)
式中:(x,y,z)为目标的真实值;(x′,y′,z′)为测量值。
2 基于机载平台的双站测向时差定位精度仿真分析
本文通过设置虚拟的布站场景,利用计算仿真分析研究机载平台双站基线长度、时差误差、测角误差以及姿态信息等对定位精度的影响。
仿真一:假设机载双站的测角误差为0.1°,测时误差为10 ns,姿态角度为0°,图2为机载双站的基线长度分别为10 km和20 km时观测区域内的GDOP分布图。

图2 基线长度分别为10 km,20 km时的GDOP分布图
从图2可知,机载双站基线长度是影响定位精度的主要因素之一,机载双站的基线距离越大,定位精度越高。
仿真二:假设机载双站基线长度为20 km,测时差误差为20 ns,姿态角度为0°,图3为机载主站的测角误差分别为0.1°和0.3°时观测区域内的GDOP分布图。

图3 测角误差分别为0.1°和0.3°时的GDOP分布图
从图3可知,当测角误差增大时,观测区域内的目标定位精度明显下降,并且当目标位于机载双站基线上的法线方向时,其定位精度明显高于其他位置。
仿真三:假设机载双站基线长度为10 km,测角误差为0.1°,姿态角度为0°,图4为机载双站的测时差误差分别为30 ns和50 ns时观测区域内的GDOP分布图。

图4 测到达时差误差分别为30 ns和50 ns时的GDOP分布图
由图4可知,同一时差测量误差条件下,目标距离机载双站越远,其定位误差越大;对于不同的时差测量误差,时差测量误差越大,对应的统一误差等高线下的观测区域越小:说明时差测量误差越大,定位精度越小。
仿真四:假设机载双站基线长度为20 km,测角
误差为0.1°,测时差误差为20 ns,图5为机载双站的姿态误差分别为0.1°(θa=θb=θc=0.1o)和0.3°(θa=θb=θc=0.3o)时观测区域内的GDOP分布图。
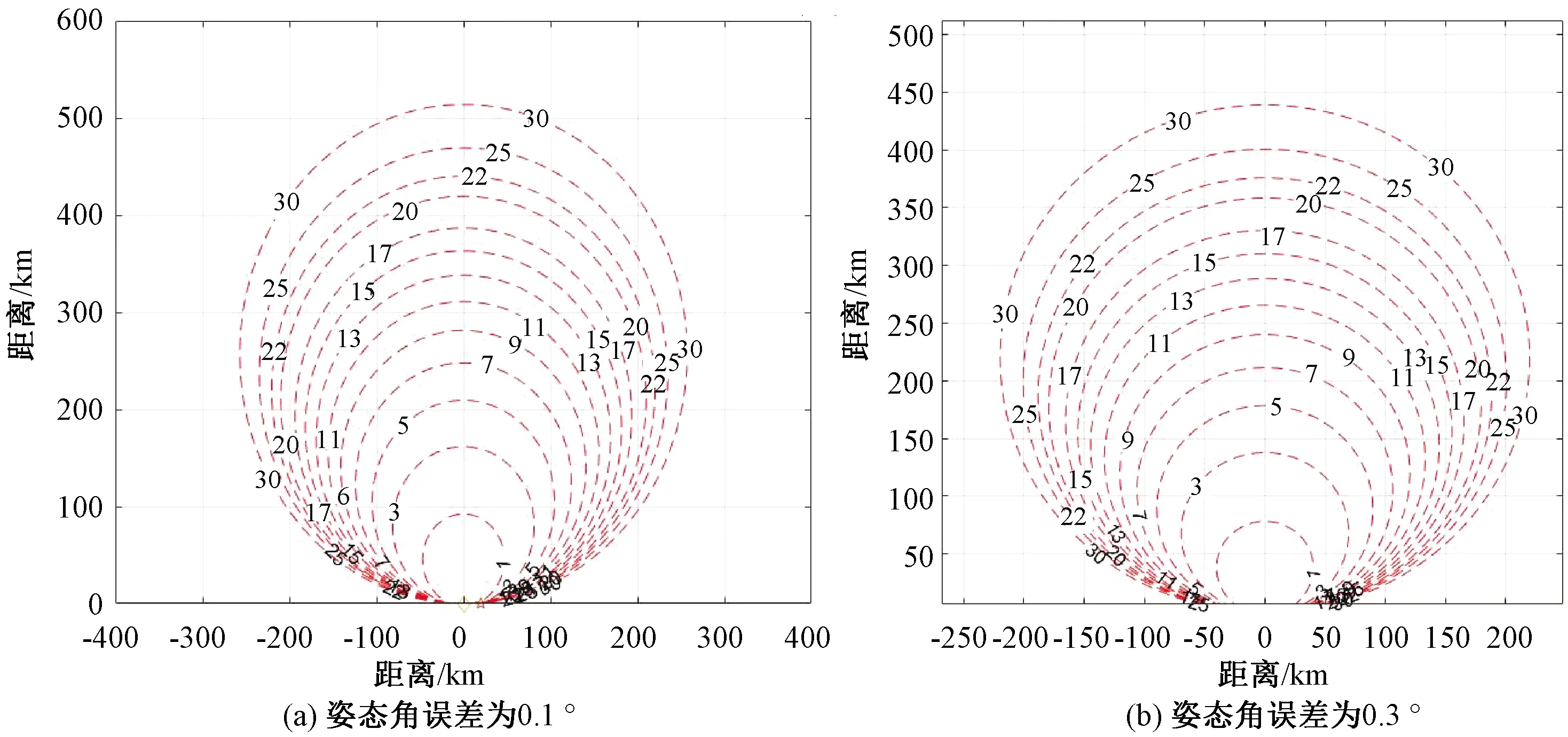
图5 姿态角误差分别为0.1°和0.3°时的GDOP分布图
由图5可知,机载双站平台的姿态角度误差越大,相同定位精度等高线内的观测区域越小,定位误差越大。但是,与机载双站的基线距离、时差误差精度以及测角误差对定位精度的影响相比较,机载双站的姿态角度误差对定位精度的影响较小。
除了机载平台双站基线长度、时差误差、测角误差以及姿态信息等影响双站测向精度之外,双站机载平台的运动速度误差对定位精度也有一定的影响。考虑双站机载平台运动速度误差主要影响了双站基线距离,在一定的定位时间之内,双站机载平台运动速度误差对定位精度的影响较小。
3 结束语
本文针对空中机载平台对地目标双站测向时差定位的应用场景,通过建立基于机载双站平台的测向时差定位模型,利用计算仿真分析在实际应用过程中的双站基线距离、测角误差、测时差误差以及机载双站姿态角度对定位精度的影响。本文的研究对基于机载双站平台的测向时差定位系统的工程应用有一定的参考意义。
