W36+离子双电子复合的理论研究
2020-08-25丁军顺符彦飙
丁军顺,符彦飙
(1.甘肃省武山县第一高级中学,甘肃 天水 741300;2.西北师范大学物理与电子工程学院,甘肃 兰州 730000)
1 概述
由于高熔点、低溅射和氚的滞留低等特点,钨被用作国际热核聚变实验堆(ITER)主腔和偏滤器区的面壁材料[1-2]。也因此钨离子会成为聚变的杂质离子。在ITER等离子体中,电离平衡是电子的碰撞电离和各种复合过程的平衡,双电子复合(DR)过程在其中起到很大的作用。因而,钨离子DR过程的研究备受关注。Schippers等人[3]在海德堡重离子储存环上对类氙W20+离子的DR过程进行了0~140eV范围内碰撞能量的实验研究。实验得出的等离子体DR速率系数与理论计算值存在较大差异。为解释、解 决 这种差 异 ,Badnell等 人[4]利 用AUTOSTRUCTURE程序包对W20+离子的DR速率系数重新进行了计算。Spruck等人也对W18+([Kr]4d104f10)[5]和W19+([Kr]4d104f9)[6]在理论计算和实验测量上进行了研究。Krantz等人[7]计算了W18+和W19+的DR速率系数。对于开4d壳层钨离子,Ballance等人[8]计算了W35+基组态为4s24p64d3的4d→4f和 4p→4d的DR速率系数。Precal等人[9]利用AUTOSTRUCTURE计算了W37+到W28+(4dq,q=1-10)的部分DR速率系数。因为开4d和开4f壳层离子DR计算的复杂性,采用能级到能级的从头计算的很少。对可能的辐射跃迁到可自电离态及其随后的级联退激(DAC)效应的计算需要耗费很多资源和时间。但在Fu等[10]和Meng等[11]的研究发现DAC效应对总DR速率系数的影响非常重要,应该给予考虑。
本文利用基于全相对论组态相互作用方法的FAC程序包[12]计算了W36+([Zn]4p64d2)离子总的DR速率系数。计算包含了 [Zn]4p54d3nln’l’和[Zn]4p64d1nln’l’(n=4,5,6,n’<24,l’<12)所有内壳层激发的能级。考察了不同激发与辐射通道对DR速率系数的贡献,考虑了所有可能辐射跃迁到可自电离态及级联退激(DAC)的影响,并进一步的利用外推的方法外推了n’=24-1000的结果。
2 理论方法
W36+离子俘获一个特定能量的电子形成双激发态,然后双激发态辐射跃迁放出光子的DR过程可以简单表示为:
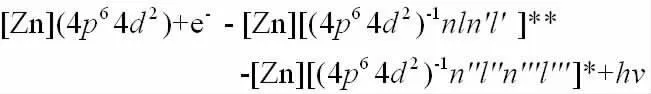
其中**表示中间双激发态j,*表示辐射跃迁末态f.由初态i经过双激发态j再到所有辐射跃迁末态f的DR速率系数:
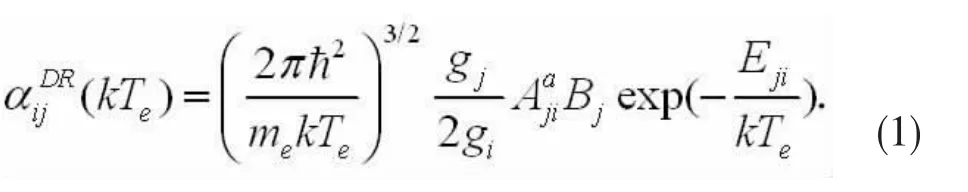
这里,Te是电子温度,k是波尔兹曼常数,Eij是共振能量,me是电子质量,gi和gj分别是态i和态j的统计权重,Aaji是由态j到i的自电离速率;Bj是分支比, 其表达式为:
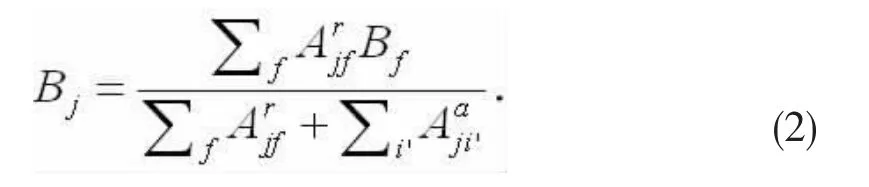
其中Aaji是态j到末态i′的俄歇速率,Arjf是态j到末态f的辐射跃迁速率,Bf是末态f的分支比,Aajf和Arjf分别由下式给出:
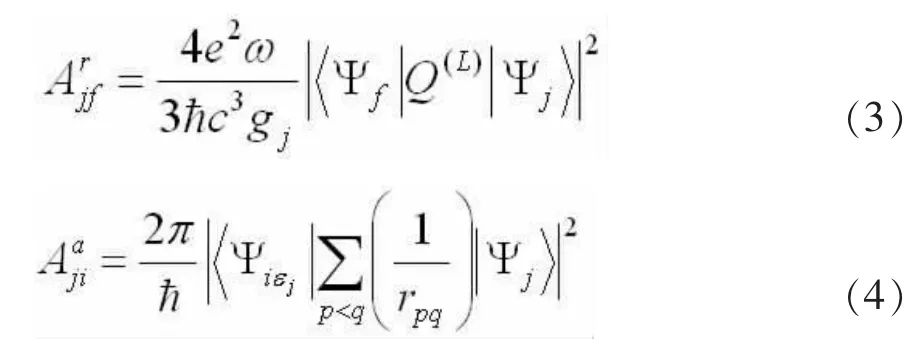
计算中,n′<24的DR速率系数通过从头计算得到,n′=24-1000的 DR速率系数通过 n′-3标度率外推得到,外推公式为:

辐射复合(RR)和三体复合(TBR)过程作为另外两种重要的电子-离子非弹性碰撞现象,其速率系数分别由如下的经验公式简单估算得到[12]:
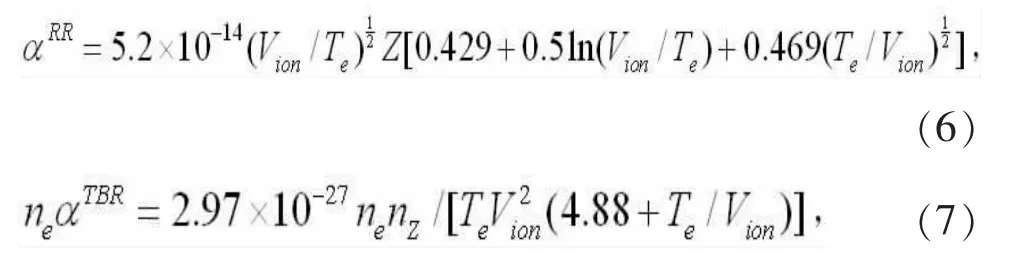
其中,Vion是电离势,Z是电荷态,nZ是对应离化态离子的最外层电子数,ne是电子密度,在本文的计算中取值1021cm-3。
3 结果与讨论
3.1 W36+离子基态的磁偶极跃迁
为考察本文计算的准确程度,表1给出了当前计算的波长λ1FAC与其他已有数据的对比。其中,λ2exp是Radtke等人[13]实验得到的数据,λ3MCDF是Pascal[14]使用MCDF计算得到的结果。可以看出,跃迁波长与实验的(最大偏差为1.60%)和MCDF计算的(最大偏差为0.44%)都符合的很好。
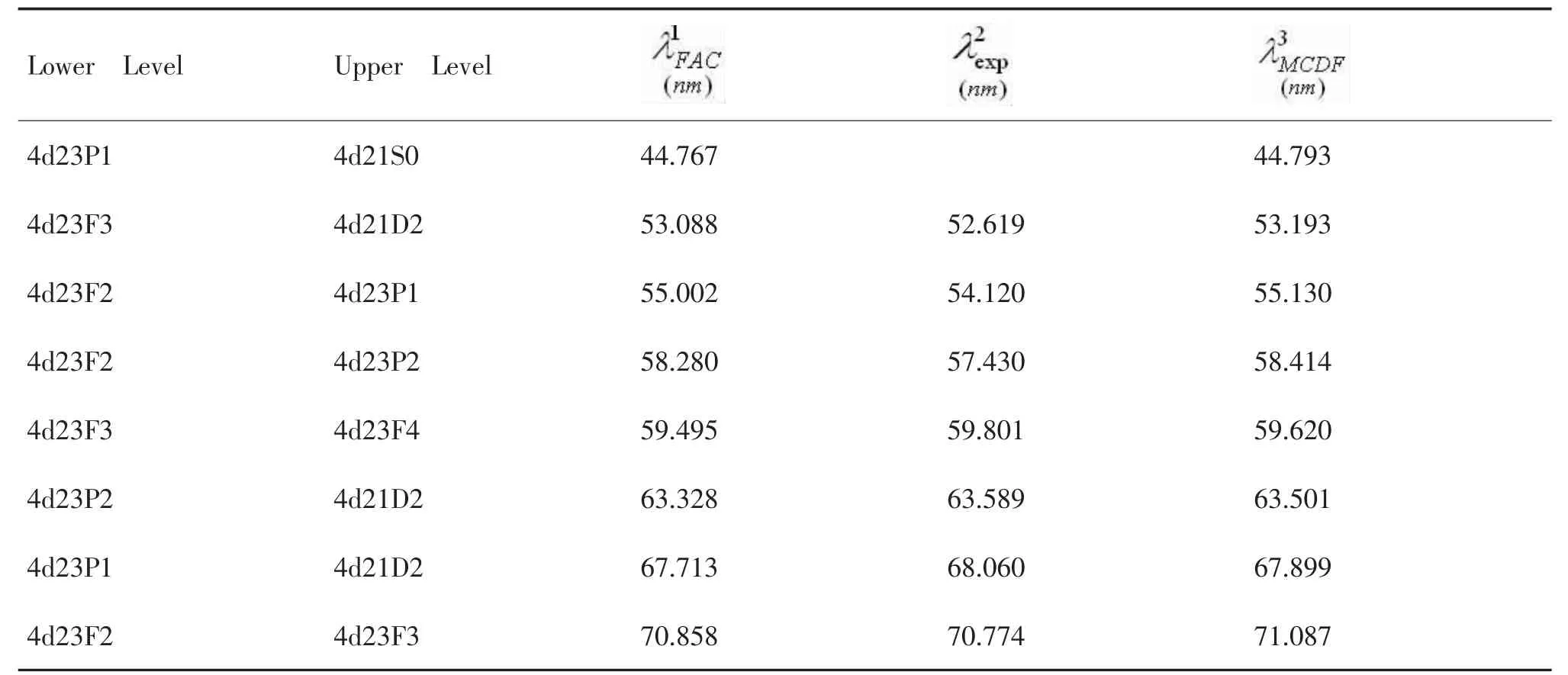
表1 当前计算的W36+离子的波长与已有结果的对比
3.2 W36+离子不同通道的DR速率系数
由于多电子离子的结构复杂且在计算中必须包含的内壳层激发有非常多的能级,使计算DR过程需要大量的资源和时间,因此有必要选择合适的DR通道,忽略一些贡献小的通道。如图1(a)所示展示W36+离子的中间双激发态j=4(s,p,d)4l12f的DR速率系数,可以看出4d激发在低温处占主导地位,4p激发在中高温(>130eV)占主导地位。4s激发的DR速率系数在全温度范围都最小,其在峰值处4s激发占三者之和的5.06%,在正式的计算中可以忽略。
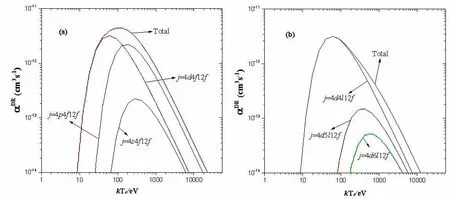
图1 W36+离子中间双激发态j=4(s,p,d)4l12f和j=4dnl12f(n=4,5,6)的DR速率系数
图1(b)给出了 j=4dnl12f(n=4,5,6)的 DR 速率系数,其中j=4dnl12f的DR速率系数最大,j=4d5l12f的仅次于j=4dnl12f的,j=4d6l12f的DR速率系数最小。其中j=4d6l12f在峰值处占三者之和峰值的1.65%,且随着n的增大,它的DR速率系数会急剧较小,因此本文计算中忽略n>6的贡献。
3.3 W36+离子的DAC效应
如图2所示,展示的是DAC、NDAC和RS+NRS的DR速率系数。RS+NRS表示同时考虑共振稳态跃迁(RS)与非共振稳态跃迁(NRS)。DAC是在考虑了RS+NRS效应的基础上进一步考虑可能辐射跃迁到可自电离态及随后的级联退激。NDAC是考虑了和DAC效应相同的第一步跃迁,但不考虑随后的级联退激。由图可见,随着温度的增大,三者的差异逐渐明显,DAC效应逐渐体现,在650eV处DAC效应的贡献为11.67%,并且DAC效应的DR速率系数的计算值与RS+NRS效应的计算值相差4.53%。在50000eV处,DAC效应的贡献是19.34%,和RS+NRS的计算值相差5.03%。因此在计算中必须考虑辐射跃迁末态分支比的影响,也就是考虑DAC效应。
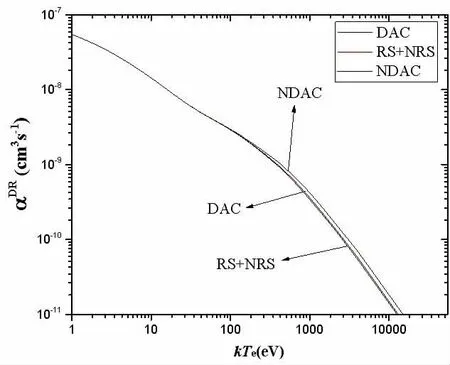
图2 DAC、NDAC和NRS+RS的DR速率系数
3.4 W36+离子总的DR速率系数
图3给出了以基态为初态的总DR速率系数,以及与ADAS数据库、辐射复合(RR)和三体复合(TBR)速率系数的比较。图中4d-total和4d-total分别表示4d和4p电子激发的总DR速率系数。4p电子激发的DR速率系数在全温度范围处于重要的主导地位,这与Fu等人计算的类锶Sn12+离子的结果类似。外推部分的DR速率系数Sum(n'=24~1000)的贡献和4d电子激发的DR速率系数接近。由图可见,DR速率系数要比RR和TBR速率系数大的多,因此DR过程在电离平衡中会起主导作用。图中OPEN-ADAS是ADPAK给出的结果,比较发现在高温处本文计算的DR速率系数与ADAS数据库提供的在曲线形状上相似,但是在低温处相差近两个量级。在1000eV处ADAS的结果比本文计算的结果大54.45%,在10000eV处大71.69%。
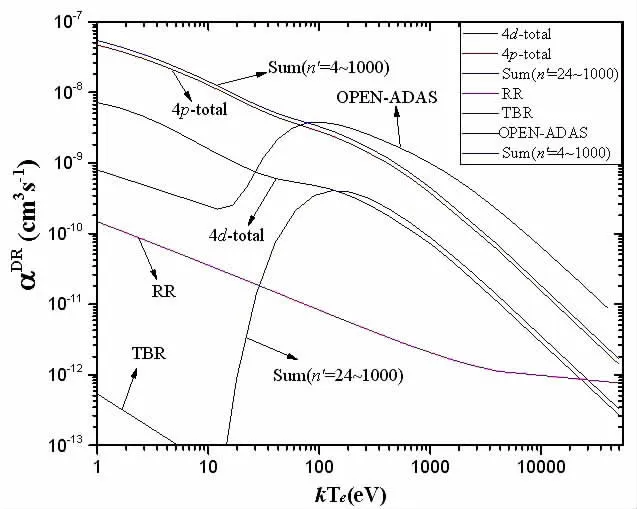
图3 W36+离子基态的总DR速率系数
为了方便使用,我们对计算得到的基态能级的总DR速率系数利用公式(8)进行了拟合:
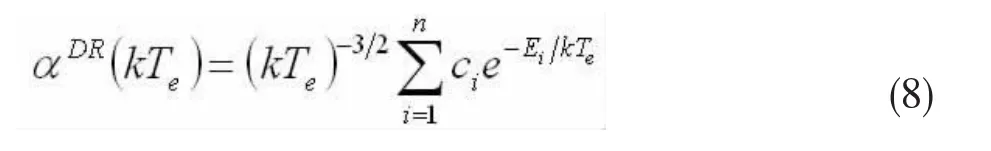
这里的ci和Ei是拟合参数,分别由表2和1给出。拟合出来的结果与我们的计算结果大部分偏差在1%以内,有极少数偏差大于1%,最大偏差为3.31%。

表2 W36+离子DR速率系数参数拟合.M[N]代表M×10N
3.5 结论
本文基于全相对论组态相互作用的FAC程序包研究了类锶W36+离子的DR过程,这是对复杂结构基组态为 [Zn]4p64d2离子首次采用详细的能级到能级的从头计算。考察了不同通道对DR速率系数的影响, 详细计算了 [Zn]4p54d3nln’l’ 和[Zn]4p64d1nln’l’(n=4,5,6,n’<24,l’<12) 所有内壳层激发的所有能级的DR速率系数,然后通过对初态做了统计权重平均,对末态逐一求和得到总的DR速率系数。计算中特别关注了辐射跃迁到可自电离态及可能的级联退激(DAC)的贡献,并考虑了非共振稳态和共振稳态跃迁(NRS+RS)对DR速率系数的影响。结果发现随着温度的增大,DAC效应的贡献越来越重要,在650eV处DAC效应的贡献为11.67%,并且考虑DAC效应的DR速率系数的计算值与考虑RS+NRS效应的计算值相差4.53%。在50000eV处,DAC效应的贡献达到最大,是19.34%,和RS+NRS效应的计算值相差5.03%。在总的DR速率系数中,4p壳层激发的DR速率系数起主导作用,在1~50000eV内,4p激发的贡献占总DR速率系数的85.54%~89.18%,但是4d激发的贡献也不能忽略。此外,我们比较DR速率系数、RR速率系数和TBR速率系数时发现,DR速率系数比RR速率系数和TBR速率系数要大很多,这说明DR过程对电离平衡的影响更为重要。最后,为了方便使用我们对基组态的总的DR速率系数做了参数拟合,拟合的结果与我们计算的结果大部分偏差在1%以内,有极少数偏差大于1%,最大偏差为3.31%。
