神经网络组合在电能质量智能控制器中的应用
2020-08-25黄文焘
虞 昉, 黄文焘
(1.国网浙江余姚市供电有限公司,浙江宁波315400;2.上海交通大学电子信息与电气工程学院,上海200240)
0 引 言
电能质量综合补偿器(UPQC)在控制电力从源传递到独立的负荷或从源传递到电网中发挥着重要作用。尽管大量的文献都出现过UPQC的相关理论,但在应用中很难找到UPQC系统,甚至在全球配电范围内也很少见。这种情况可以归因于一个事实,即UPQC理论很难理解,而其控制系统处理设备也很难实现。许多学者在与UPQC相关联的控制器的发展方面进行了大量的研究。如Ansari等提出了一个新颖的参考信号生成方法,基于模糊逻辑算法的UPQC[1-3]。在基于三相四线统一电能质量来补偿电能质量方面,Engin等提出了同步参考坐标变换(SRF)的控制方法理论[3]。本文提出一个简单且能够循序渐进的电能质量综合控制方案,与传统的电能控制器模型相比,提出的综合控制方案具有较强的有效性以及时间性[4]。
1 UPQC模型的建立
通常情况下,UPQC由2个通过一条公用直流母线连接起来电子变流器组成。在约束功率交易过程中,这2个转换器利用4个控制器进行电流交换。并联变换器是一个直流侧和三相交流侧三臂型三相桥变换器。三相交流端在共同耦合点,通过电压互感器和一系列反应堆连接在三相交流母线,如图1所示。

图1 统一UPQC结构图
一个脉冲宽度调制(PWM)信号发生器产生同步切换脉冲,切换三臂并联变换器的6个开关,并联变流器的目标可以通过切换脉冲实现,切换脉冲的生成是由2个控制器产生的三相参考信号控制。2个控制器的控制目标是影响参考信号的生成,从而使转换器的操作满足要求。图2显示了2个控制器的位置以及它们的输入和输出信号。第1个控制器是用来控制实际直流环节电压和所需的直流环节电压之间的误差为零;第2个控制器是用于控制实际的共同耦合电压与所需共同耦合电压之间的误差为零。这2个控制参数和相关的操作参数是调制指数(MI)的系数和幅度。

图2 一般控制图
源侧三相电压Ua、Ub和Uc符合正弦曲线,这些量要转化为等效直流量,然后应用于控制器。转换的三相正弦电压表示为Uabc变为Ud,Uq,Uo,在旋转坐标系中,称为DQ 变换或派克变换。向量(Ua、Ub、Uc)可以通过变化矩阵转换为另一个向量(Ud、Uq,Uo):
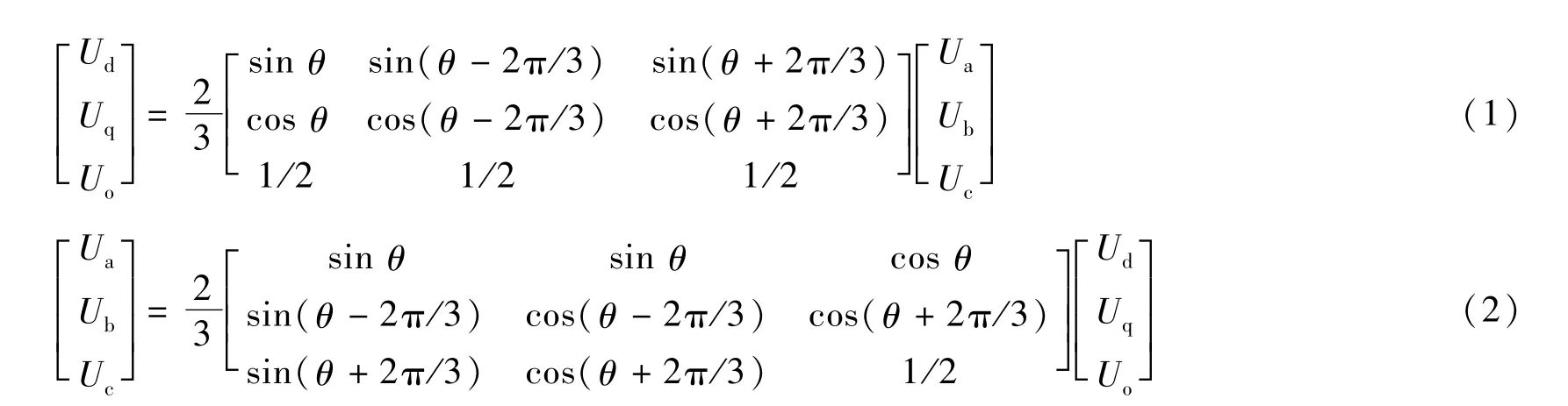
向量(Ua、Ub,Uc)和变换矩阵的元素是随时变化,但输出向量Ud、UqUo不随时间变化,而向量Ua、Ub、Uc的任何变化都会在Ud、Uq、Uo中有所反映。派克变换的三相电压系统的变换,在正弦曲线中120°位移后,成为另一个系统3个常量。在变换系统中,如果三相系统平衡,Uo为0。Ud和Uq矢量是正交的且对彼此无任何影响。在一个典型的控制系统中,Ud和Uq可以单独变化,不影响其他。
2 综合神经网络
以上述理论为基础,本文设计了4种模糊逻辑控制器,其中2个分别为系列转换器和并联变换器。这4种模糊逻辑控制器适当调整均可达到预期性能。而这4个控制器可被4个单独人工神经网络取代,其后,4个控制器的2个输入和1个输出端被单独人工神经网络的8个输入和输出端取代。而考虑到若是4个人工神经网络所取代1个单独的人工神经网络,操作的速度和系统的动态性能都会有所提高[5-6]。
在模糊逻辑控制器模型运行环境下,错误、错误率和模糊逻辑控制器相关的输出用于训练人工神经网络。同时采用相同的步骤收集其他输入/输出数据。使用神经网络形成4个人工神经网络,且每个经过训练,对输入和输出数据作出相应的反应。而通过使用UPQC模型重新安排与人工神经网络在模糊逻辑控制器中的位置。整个UPQC系统的性能在可能导致电能质量扰动的不同负荷条件下,由于被4个人工神经网络控制,可被观测到。根据观测该控制方案下4个人工神经网络工作状态正常[7]。然后,删除4个人工神经网络后,UPQC模型与CNN已经重新安排。与4个CNN相关联的输入和输出路线分布在CNN网络。整个UPQC系统的性能由CNN控制,在可能导致电能质量扰动的不同负荷条件下可被观测到。
突触权重在ANN形成初期且可随机初始化,但在第1次训练阶段,根据学习规则突触权重要经历形态变化。最后,训练结束后,每个突触权重达到其最终值。在测试阶段期间,ANN调成模拟功能。既使有输入值,突触权重不改变,只是与神经元共同工作输出[11-13]。一个CNN反馈为反向传播类型,其基本形式有一个输入层、隐层和输出层。而隐层内的数量可能不止一个。因模型试验的复杂性,本文仅考虑只有一个隐藏层的CNN情况。CNN模型采用的形式如图3所示。实际上,由于人工神经系统的组合,结果ANN出现更多数量的输入和输出,隐层神经元的数量是相同的。因此,所有相结合形成ANN的神经网络,分享共同的隐层神经元。以演示人工神经网络如何相结合工作举例,考虑以下两个非线性方程[14-15]:

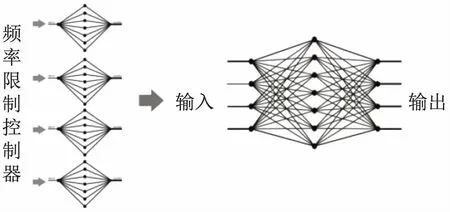
图3 CNN控制模型
考虑两个独立训练的人工神经网络的输入/输出数据集,设置时间范围在0~1之间,在步骤0.01中,如方程(3)和(4)所述。在MATLAB/SIMULINK环境中,创建和培训两个人工神经网络,两个测试模型用于测试这两个网络的性能。然后创建含有两个输入和两个输出的第3个人工神经网络。
3 模拟结果
本文中控制策略描述的CNN模型如图4所示。通过对比UPQC的多功能控制结果,体现了综合神经网络控制器的作用。在不平衡条件下,电源电压在电压跌落和骤升情况下的扭曲图[8-10],如图5(a)所示。补偿电压跌落和骤升,使用PI控制器,模糊逻辑控制器,ANN控制器和CNN控制器的情形如图5(b)所示。从图5(b)可见,在电压骤升经过补偿后,PI、FLC和ANN控制器对应的每单位值分别为1.083,1.038,1.102。而CNN控制器电压骤升经过补偿后,对应单位值为0.983(最接近单位)。类似地,在电压跌落经过补充后,CNN控制器对应的单位值最接近(0.994)。负荷电压保持恒定值,不考虑电压源的电压跌落和骤升幅度。在这种情况下,通过创建网络系统上的不平衡负荷,可以分析电压跌落和骤升情况。电压跌落的时间是0.5 ~0.1 s和电压骤升持续时间为0.15 ~0.2 s。供应电压不平衡正弦值每单位低于1。串联补偿器注入电压,负荷侧维持平衡正弦电压。负荷电压维持在每单位1标准值。UPQC在补偿电压跌落和骤升情况下,通过PI控制器,模糊逻辑控制器,ANN控制器和CNN控制器如图5(b)所示。
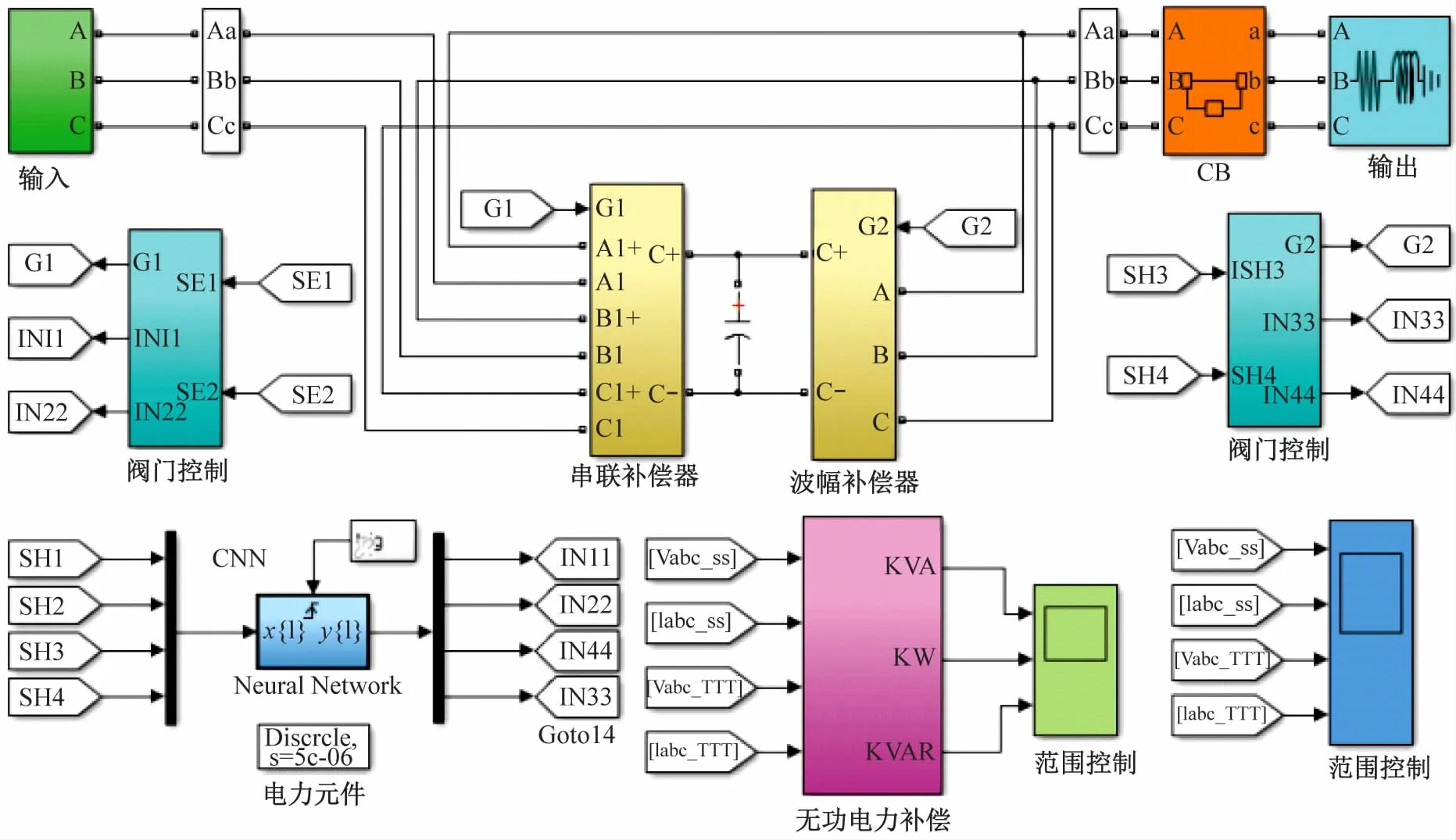
图4 CNN模型

图5 (a)电压暂降(b)膨胀的源极电压
PI、PLC和CNN控制器的性能分析如表1所示。从结果来看,CNN控制器谐波失真值保持在允许的范围内。电源电压失真条件下,在0.5~0.1 s发生跌落状态。电源电压跌落/骤升补偿前在R阶段失真2.66%。负荷电压跌落/骤升补偿后在R阶段分别近为1.90%。创建一个不平衡负荷条件下,并联补偿器的负荷电流强制为正弦值。源电流补偿之前谐波失真2.46%。补偿后的电流谐波失真1.21%。因此在不同的控制器操作下,从表1可以很明显看出,CNN控制器在补偿后,减少电压和电流谐波失真性能更佳。谐波失真在IEEE特定范围519~1 922。图6显示,电压跌落和骤升状态下,负荷电压保持恒定。图6(a)显示了带负荷源侧电压跌落和骤升状态下有功功率和无功功率。图6(b)显示模拟时间0.15 ~0.20 s,负荷侧的有功功率和无功功率补偿输出结果。

表1 PI、FLC和CNN控制器性能分析
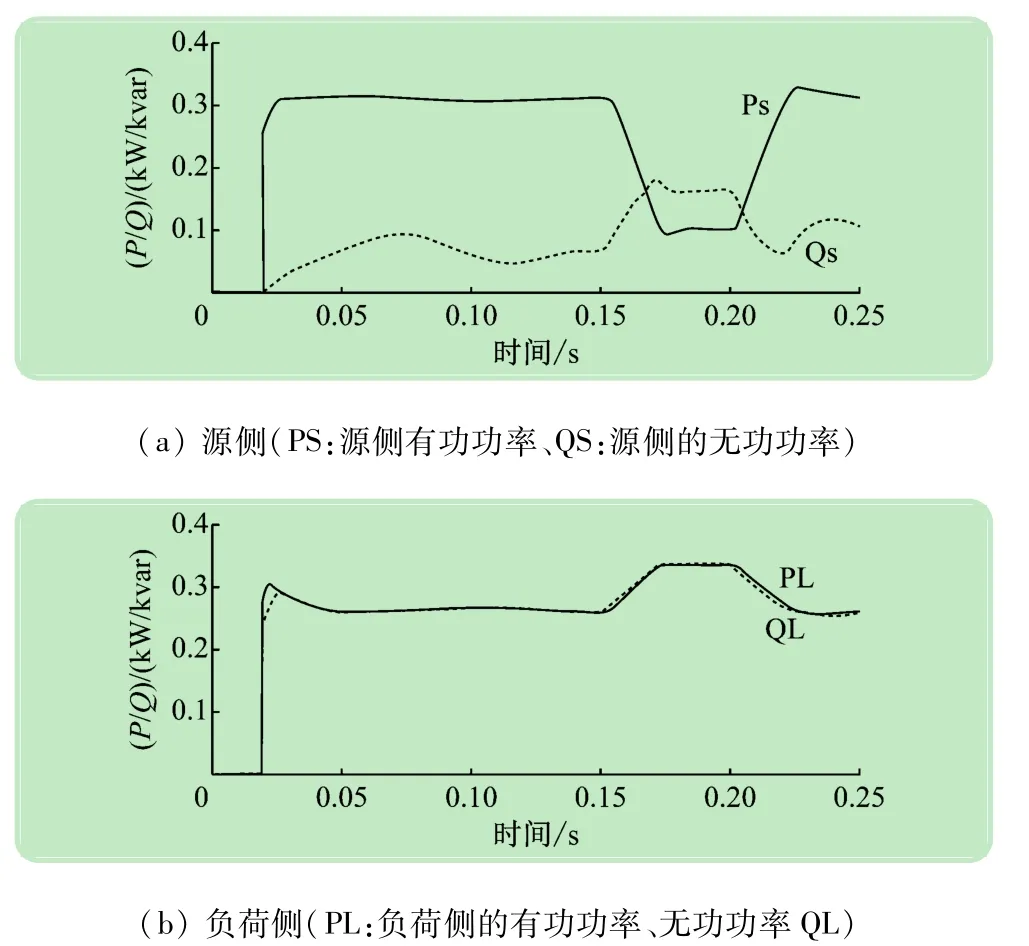
图6 电源和负荷侧的实际和无功功率
表2显示,单一ANN控制器下源电流谐波失真2.68%而CNN控制器下失真是2.46%。同样地,单一的ANN控制器下负荷电流谐波失真是1.69%,CNN控制器是1.21%。电源电压、负荷电压、源电流和负荷电流在CNN控制器下谐波失真如图7所示。电源电压在CNN控制器下总谐波失真(THD)是2.66%,负荷电压是1.90%。电源电压在ANN控制器总谐波失真(THD)是2.96%,负荷电压是2.16%。源电流在CNN控制器下,总谐波失真(THD)2.46%,负荷电流1.21%。源电流载在ANN控制器补偿前总谐波失真(THD)2.68%,补偿后负荷电流谐波失真降低1.69%。从模拟结果观察,CNN控制器的谐波消去性能法比ANN控制器和常规控制器更佳。

表2 ANN和CNN控制器性能分析

图7 CNN控制器R相THD水平
4 试验结果
通过模拟得到CNN的结构,可以很容易地应用于KEIL C(串行编程器源程序),并嵌入微型控制器。CNN使用的S型函数,可通过下述编程部分实现。程序包含的S型函数可以作为一个C型函数,由CNN主程序多次调用。MATLAB模拟CNN单位的突触权重为常量和在keil运用中,突触权重为浮点常量。训练有素的CNN控制器使用微型控制器进行模拟在负荷突然变化情形下,形成电压跌落和骤升。
图8显示了在电压跌落状态下的试验结果。图8(a)显示的不平衡电源电压和相应的谐波失真为2.79%。图8(b)显示了补偿负荷电压和对应的谐波失真为1.98%。负荷电压保持恒定值。

图8 电压骤降和谐波
电压骤升条件下试验结果如图9所示。增加的电源电压及相应的谐波失真为2.79%,如图9(a)所示。相对应的补偿负荷电压和谐波失真为1.98%,如图9(b)所示。串联转换器用于注入电压、补偿负荷电压。
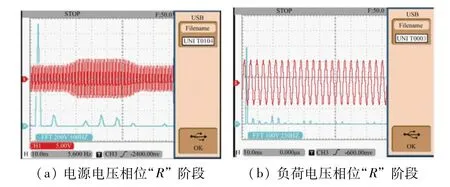
图9 电压骤升和谐波
不平衡负荷条件下,源电流(跌落)扭曲和失衡情况如图10(a)所示,相应的谐波失真为2.52%。电流补偿的试验结果如图10(b)所示,负荷电流的谐波失真测量值是1.29%。
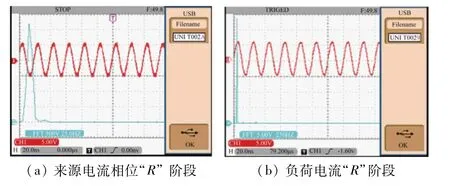
图10 凹陷电流和谐波
不平衡负荷条件下,源电流(骤升)扭曲和失衡情况如图11(a)所示,相应的谐波失真为2.52%。当前补偿的试验结果如图11(b)所示,负荷电流的谐波失真测量值是1.29%,1 V等于1 A。由此可知,源电流波形是非正弦型,而补偿负荷电流的波形本质上是正弦的,由于并联变换器的作用,负荷电流维持平衡和正弦波形。因此在CNN控制器作用是消除谐波和补偿电压。试验结果中,电压和电流谐波失真补偿后的水平如表3所示。

图11 膨胀电流和谐波

表3 试验结果数量/R相
由表3可知,负荷电压和负荷电流补偿后谐波失真水平分别为1.98%和1.29%。
5 结 语
基于CNC控制器的人工智能系统,运用综合神经网络设计了4种模糊逻辑控制器,其中2个分别为系列转换器和并联变换器。这4种模糊逻辑控制器适当调整均可达到预期性能;而这4个控制器可被4个单独人工神经网络取代,其后,4个控制器的两个输入和一个输出端被单独人工神经网络的8个输入和输出端取代。而考虑到若是4个人工神经网络所取代一个单独的人工神经网络。该系统可提高配电系统的电能质量。数值模拟模型和原型模型试验显示,可以实现较高的额定功率。采用此种系统可达到稳定状态和瞬态响应。
