基于数据流的多源并行高可靠数据容灾算法
2020-08-25孙也,丛岩
孙 也, 丛 岩
(1.吉林广播电视大学教务处,长春130000;2.空军航空大学模拟训练中心,长春130022)
0 引 言
本文提出一种基于数据流的多源并行高可靠数据容灾算法(MultiSourceParallelHighlyReliable Recovery,MSPR),该算法采用“一对多”的形式对数据进行快速备份和恢复,容灾对象服务器通过网络与多个备份服务器相连形成多点结构,将容灾对象服务器的数据以数据流的形式传输到备份服务器中,存储多个副本,利用相连接的多处备份服务器结合负载均衡技术并行下载差异数据。MSPR算法可充分考虑各个服务器的实际负载能力,合理分配数据传输任务,通过快慢协调保证数据恢复过程的同步与一致性。
1 MSPR算法分析
MRDBR算法[7-9]在对各个备份服务器分配任务时没有考虑各个备份服务器的状态差异,利用平均原则进行分配,这样虽然简化了分配的时间和资源开销,但是由于各个链路负载不同、服务器性能不稳定等因素,容易出现完成任务时间的严重不平衡情况,给再分配工作带来巨大的压力[10]。另外,数据在传输过程中缺乏必要的校验机制,会造成资源和时间成本的浪费。鉴于以上问题,对MRDBR算法进行改进,提出一种基于数据流的MSPR,可以满足以下要求:①利用负载均衡思想[11],在恢复任务初次分配上,根据各个备份服务器不同的负载状态进行分配,使分配更加均匀合理;②在数据传输过程中,加入针对一定数据粒度的校验机制,避免数据传输前后不一致造成的资源浪费[12]。
MSPR具体算法分析如下:
设本地服务器P发生灾难时,已经将本地数据D备份到不同位置的n台备份服务器{S1,S2,…,Sn}中,数据大小均为d,而在P中灾难发生后保留可用的数据为E,MAPR算法仅仅恢复E与D的差异部分F,从而减小工作量,提高恢复的针对性,差异F=D-(E∩D),大小为f且f<d。设方案整体的平均恢复速度为vw,恢复的整体时间tRTO=f/vw,为了将tRTO降到最小,MAPR算法的核心任务是合理分配链路和并行恢复数据,并在考虑本地主机性能和硬件成本的情况下使vw达到一个最佳值。在分配传输任务前,要对各个备份服务器负载情况进行预分配,在分配过程中根据各个链路传输速度以及完成情况进行任务的动态调整再分配。
在预分配阶段,各个备份服务器的负载指标作为最重要的参考,设N台备份服务器对应的负载为Loadi(t),代表第i台备份服务器在时刻t的负载情况。负载作为一个综合性较强的指标,主要与t时刻第i台备份服务器CPU使用率Ci(t)、内存占用率Mi(t)、磁盘I/O 占用率Ii(t)和响应时间用率Ri(t)有关,具体表达式为:式中:w1、w2、w3、w4分别表示CPU 使用率、内存占用率、磁盘I/O占用率和响应时间对整体负载的影响权值,且w1+w2+w3+w4=1。
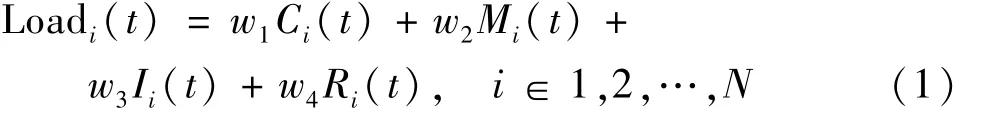
不同情况下,各参数对负载的影响并不是一成不变的,因此权值也是根据具体的环境与实验分析所确定的。在获得负载指标后,根据下式将所要恢复数据F进行分配。

式中,Fi表示第i台备份服务器所需要传输的数据任务。
土体和直根的物理属性和测试模型的物理属性基本保持一致。土体和直根的泊松比0.3,密度2 000 kg/m3,土体杨氏模量1×106 Pa;直根杨氏模量1×107 Pa。摩擦系数定为0.5;重力加速度为10 m/s2;弹性滑动值一般设为总接触长度的1%;拔出距离同具体只跟尺寸有关。
再分配阶段负责动态调整任务分配,主要是由于预分配后,各个备份服务器在执行过程中由于状态的变化和不确定因素影响了恢复速度,常出现某一台或几台备份服务器已完成了相应的传输任务量,而其他备份服务器任务却没有结束。设这种情况为t0时刻,某台服务器SS已经完成预分配任务,此时将预计最长时间完成的备份服务器Sl的任务按照一定比例分配给SS。在分配阶段,主要考虑各个服务器链路传输平均速度和剩余数据大小,通过算式max{f′1/¯v1,f′2/¯v2,…,f′n/¯vn}找出最长恢复时间的备份服务器,并将未完成的任务量根据下式分配给SS共同完成。

式中:f″S、f″L分别代表备份服务器SS、Sl再分配后的任务量;LoadS(t0)、LoadL(t0)为备份服务器SS、Sl在t0时刻的负载;¯vS、¯vL为备份服务器SS、Sl恢复数据过程中的平均速度;β为服务器当前负载对传输任务重新分配的影响系数。
本地服务器与备份服务器Si在连接过程和传输过程中所需要的总时间ti为
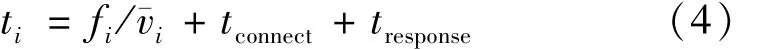
式中:tconnect为本地服务器与备份服务器建立连接所需要的时间;tresponse为每次数据请求的响应时间。这两段时间数据并没有传输,带宽没有得到利用。为了避免数据分散过细导致总的数据响应时间与连接时间延长,从而造成资源浪费,设置一个数据阈值δ,当再次分配时,预计最长时间未完成的任务数据量f′L<δ时,不需将剩余部分再分配给其他服务器。
为保证MSPR算法数据传输过程数据恢复的一致性,首先将要传输的数据按照一定大小分成j个数据块,余出部分同样分在一起。然后在备份服务器数据发送端对数据流进行分析,并计算出每个传输数据块的特征值,通过对比判断确定数据传输前后的一致性。
2 MSPR算法流程
当本地服务器发生灾难,造成数据丢失时启动MSPR算法,整个算法分为前期处理阶段、预分配传输阶段、再分配传输阶段以及校验阶段,具体流程如图1所示[12-15]。

图1 MSPR算法流程
(1)前期处理阶段。当灾难发生时,首先由F=D-(E∩D)获取需要恢复数据部分,确定需要恢复数据内容F和大小f后,由本地服务器P向各个备份服务器{S1,S2,…,Sn}发送传输请求,同时记录各个备份服务器的反馈负载信息Loadi(t)。
(2)预分配阶段。在获得各个备份服务器的负载信息Loadi(t)后,根据式(2)划分数据,完成预分配恢复任务,并对各备份服务器发送相应的备份服务器恢复的任务记录Ri,格式为:
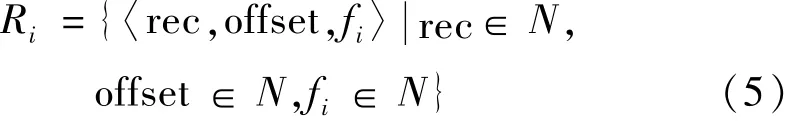
式中:rec为容灾表示;offset为对应备份服务器所要恢复任务的偏移地址;fi为对应备份服务器需恢复数据大小。
各个备份服务器在接收到来自本地服务器发来的任务记录后,按照指定的偏移量及数据大小读取各自数据Fi,同时根据MD5算法在传输端利用函数H(Fi)算出数据Fi的特征值γbi,存储任务记录反馈R′i中发送给本地服务器。记录反馈格式为:

本地服务器接收到来自各备份服务器的数据,将数据按照偏移量进行顺序存储,逐步完成数据的恢复。
(3)再分配阶段。当其中的某个备份服务器完成其分配的任务时,需要按照式(3)将此时预计需要最长时间完成的备份服务器Sl的任务分配给SS,并执行预分配之后的步骤。为了减小不必要的再分配造成时间响应浪费,设置一个数据阈值δ,当再次分配时,预计最长时间未完成的任务数据量f′L<δ时,不必将剩余部分再分配给其他服务器。
(4)数据校验阶段。数据校验阶段贯穿于数据恢复的整个过程,在备份服务器的数据发送端利用WinPcap将数据流捕获并进行分析,并结合MD5算法计算出一定大小χ传输数据块的特征值γbij,当对应数据在本地服务器接收后再次利用函数H(Fi)算出对应接收数据的特征值γaij,通过判断是否满足γbij=γaij来确定数据传输前后的一致性,以保证数据恢复的准确性,若γbij≠γaij需要重新传输对应的数据块。
3 MSPR算法测试
为验证MSPR算法整体的有效性和各项性能,在千兆局域网中搭建实验环境,包括本地主服务器1台,备份服务器6台。服务器CPU型号为Intel E5-2600 V4,8GB 内存,操作系统为Windows Server 2008,本地服务器的网卡带宽为1 Gb/s,备份服务器的网卡带宽为100 Mb/s。其他参数配置见表1。

表1 实验环境参数
3.1 测试结果
测试分为6组,每组实验所需要的备份服务器的数量分别为1~6。在测试过程中,各备份服务器持续不断地向本地服务器传输数据,分别测得每组实验中组内所有备份服务器的数据恢复速度。考虑到初始传输状态数据传输速度不稳定,测量过程以第10 s时间为基准,在输出开始10 s测量各组中各个服务器的数据恢复速度,则不同备份源服务器的数据恢复速度如图2所示。
测得备份服务器数量变化情况下,各组实验本地服务器数据恢复的整体速度,时间从0 s开始,如图3所示。
实验证明,在一定范围内,本地服务器的数据恢复速度与并行连接的备份服务器数量呈明显的递增趋势,充分证明了利用多源并行数据恢复可以利用多条链路带宽,大幅提高数据整体恢复速率。利用恢复算法进行并行恢复过程中,各个链路达到速度稳定值所用时间为3~4 s,具有比较短的初始响应时间。当备份服务器数量达到5以上时,本地服务器数据恢复速度受制于处理性能和存储性能,达到本地服务器网卡带宽值的60%左右,恢复速率不能继续增长保持在一定水平收敛。因此,考虑到资源成本利用的最大化,为了达到最佳恢复速率且兼顾成本代价,本实验环境备份服务器设为4或5。
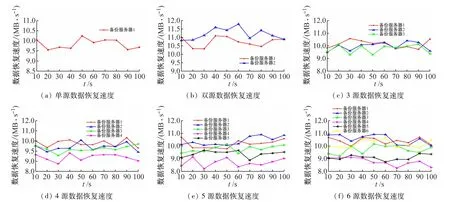
图2 不同备份源服务器的数据恢复速度

图3 本地服务器数据恢复的整体速度
3.2 性能对比
备份服务器数量分别设为5,设置恢复数据大小为1~10 GB,测试本文改进算法MSPR与传统多点恢复数据MRPTC算法的恢复时间。其中,MRPTC采取数据恢复链路平均分配的方法,分配系数σ=0.2。两种算法恢复时间RTO对比结果如图4所示。
在传输速率上,设置恢复数据大小为10 GB,备份服务器数量为5,在10~150 s测得两种算法整体恢复速度如图5所示。
在可靠性上利用第3方特征值计算工具MD5sum,分别设置恢复数据大小为1~10 GB,测试恢复数据在传输前和恢复后是否一致,两种算法恢复数据的错误率对比如图6所示。

图4 两种算法RTO对比
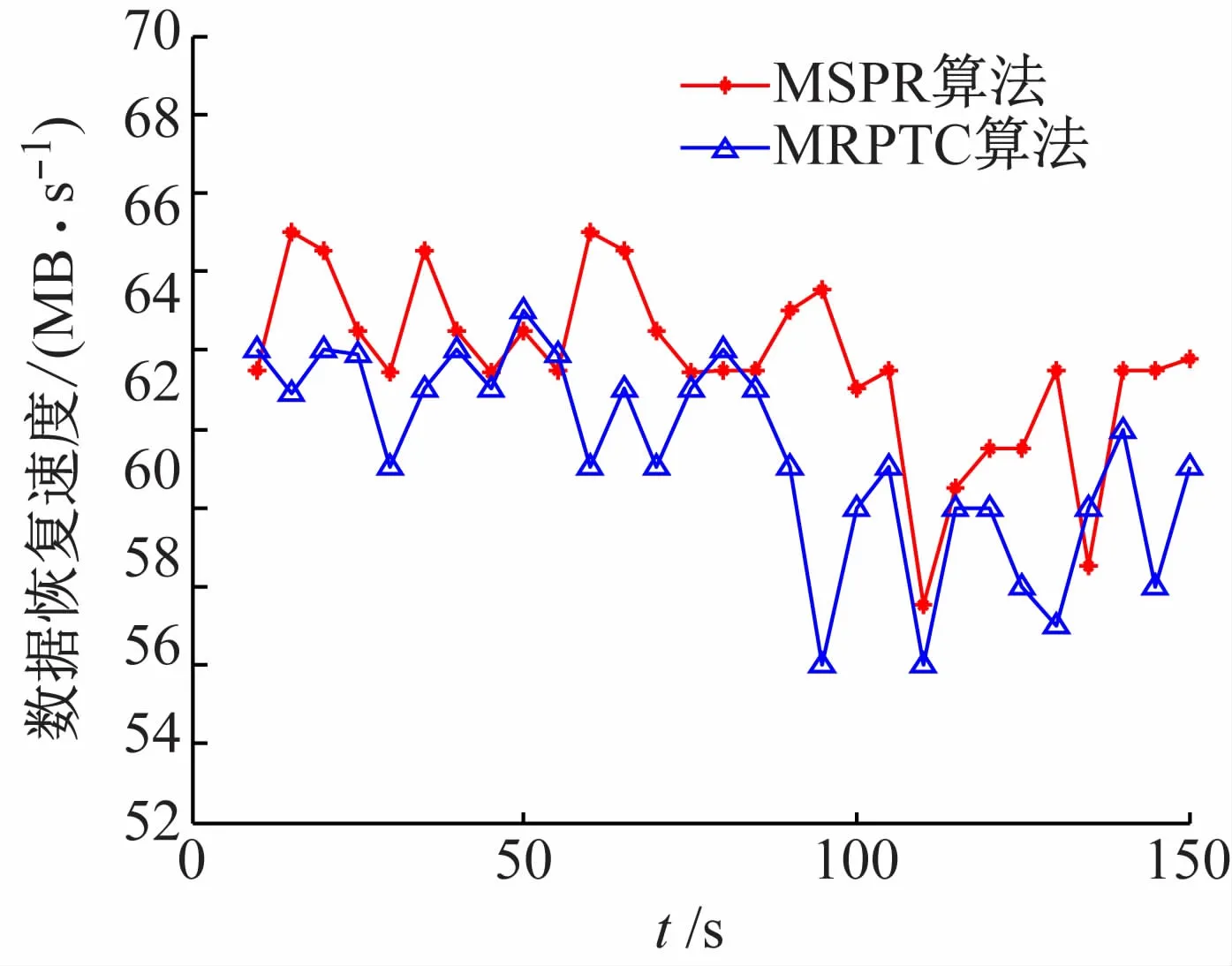
图5 数据恢复速度对比图
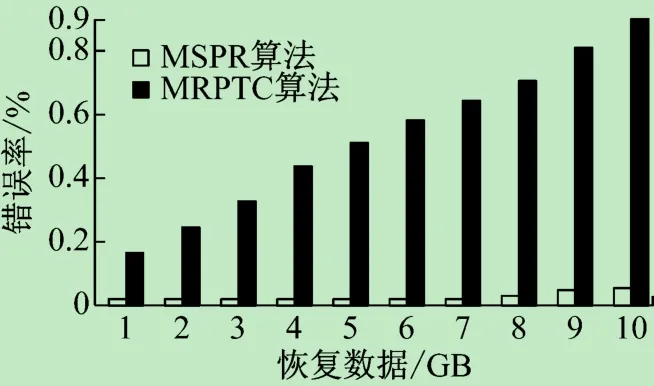
图6 错误率对比
RTO对比实验证明,两种算法在相同恢复任务的情况下,MSPR算法充分利用多条链路带宽,整体恢复速度更加迅速,当恢复数据超过3.5 GB时恢复时间指标具有明显优势。数据恢复速度测试结果再一次验证了MSPR算法按照各路实时负载情况分配任务比MRPTC算法更加合理,减小再分配阶段的次数和复杂性。从数据传输过程速率波动次数可以看出,MSPR算法提高了首次分配准确性,正是由于MSPR数据传输过程速率波动次数少且更加平稳,从而提高了整体传输速度。数据恢复错误率实验说明在可靠性方面,MSPR算法在传输两端加入特征值验证环节,因此数据恢复错误率几乎为0,当恢复数据增加时MSPR算法并没有随着恢复数据的增大而明显增加,可以证明这种特征值验证方式在不明显提高时间成本情况下,有效提高了数据传输与恢复过程的可靠性。
4 结 语
本文给出一种基于数据流的多源并行高可靠恢复算法MSPR,这种算法在传统多源恢复方案的基础上,通过改进普遍使用的MRPTC算法得到,可满足信息系统高可靠应急的需求,实现在极短的时间锁定所需的目标数据并准确恢复的功能。研究结果表明,该算法对于初始任务的分配更合理,减小了再分配阶段的次数和复杂性,从而提高了整体传输速度,且具有校验机制,在传输可靠性上具有明显优势。
