主成分回归模型下智能农机对耕深的影响研究

赵嘉琦 高阿芳 闫新洋 曾繁湫 李思源

(1.长春工业大学数学与统计学院，吉林 长春 130012)

1 研究设计

1.1 数据选取

本文所用数据为吉林省长春市试验农田采集的真实有效数据。

1.2 方法选取

农田采集的数据各变量相互关联，量化分析可以避免数据之间存在复杂的共线性。主成分回归模型先对主成分进行分析，选取代表性的指标替代原有指标，并反映原指标较为全面的信息，且结果准确无误，具有典型性。

1.3 指标选取

国内外各研究者对农业研究的指标选取有所差异，通过资料的查询及农田实地的考察，选取异于常人的指标进行研究，如下表1为本文所选取的几个指标。

1.4 方法说明

1.4.1 主成分

主成分分析是变量相关关系的一种多元统计方法，其步骤为：选择最初研究指标；求其特征根与特征向量；查看kappa值，若大于100，先消除共线，再进行下一步操作；通过碎石图选取主成分个数，为进一步确定准确的主成分个数，查看特征值及累积贡献率，若累积贡献率大于80%，则选取前面相对应的指标；获取的结果结合实际情况进行分析。

1.4.2 主成分回归模型

(1)模型。

Y=β0+β1X1+β2X2+β3X3+β4X4+β5X5+β6X6+μ

(2)回归分析。

运用Python、R软件录入数据，先进行主成分分析，将获得的主成分综合加权并采用逆变换法，得到原始变量的综合关系式。

2 实证分析

2.1 相关矩阵

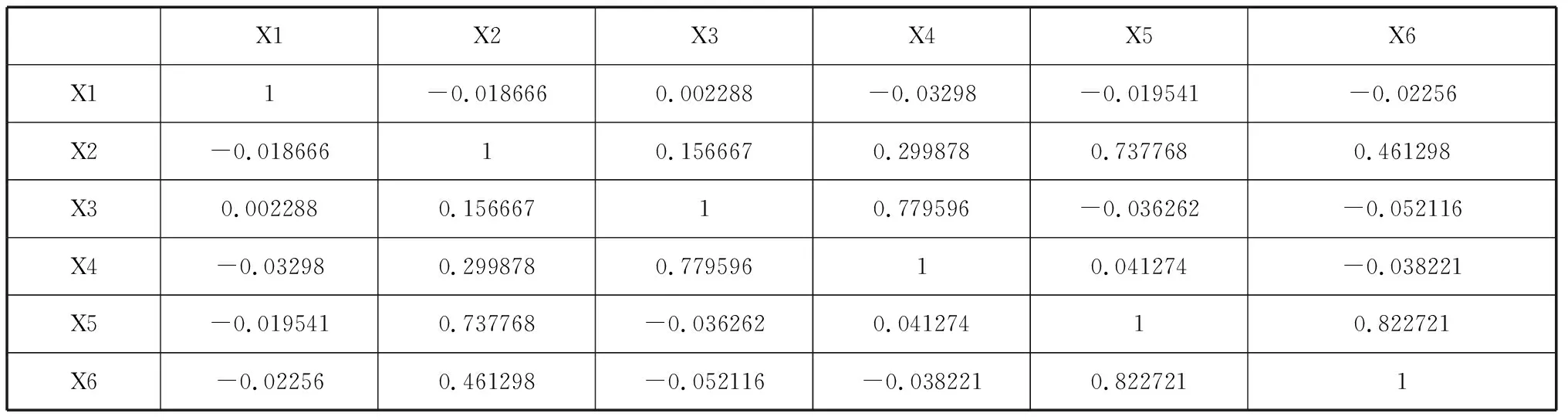
表2 相关矩阵

由上表2，指标间的相关系数矩阵数值可以看出变量间具有相关关系。为了降低数据维度，我们对指标进行因子提取，虽然这些指标之间的单位相同，但为了后文数据的一致性，对其进行标准化处理，并进行因子分析。

2.2 碎石图

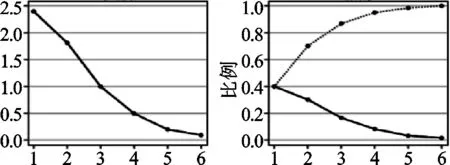
图1 碎石图

从图1中可以看出前3个主成分的提取对原变量信息的刻画有显著作用，为此我们抽取3个固定的因子数量，并得到下表。

由表3可知，前3个主成分X1、X2、X3的累积贡献率为86.84%，大于80%。因此，对第三主成分以后的主成分完全可以忽略不计，即取前3个为主成分代替原来的六个指标，起到了降维的作用。

2.3 特征值及累积贡献率

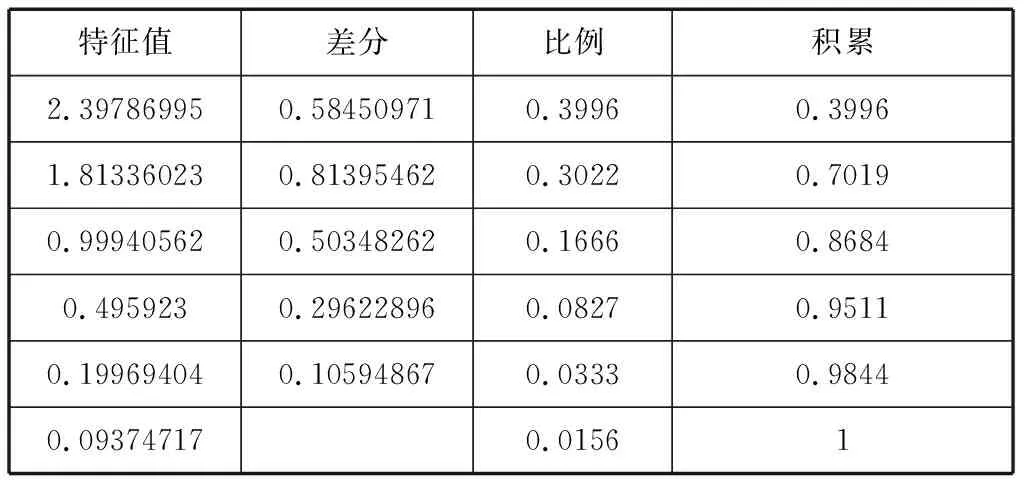
表3 特征值及累积贡献率

2.4 主成分得分

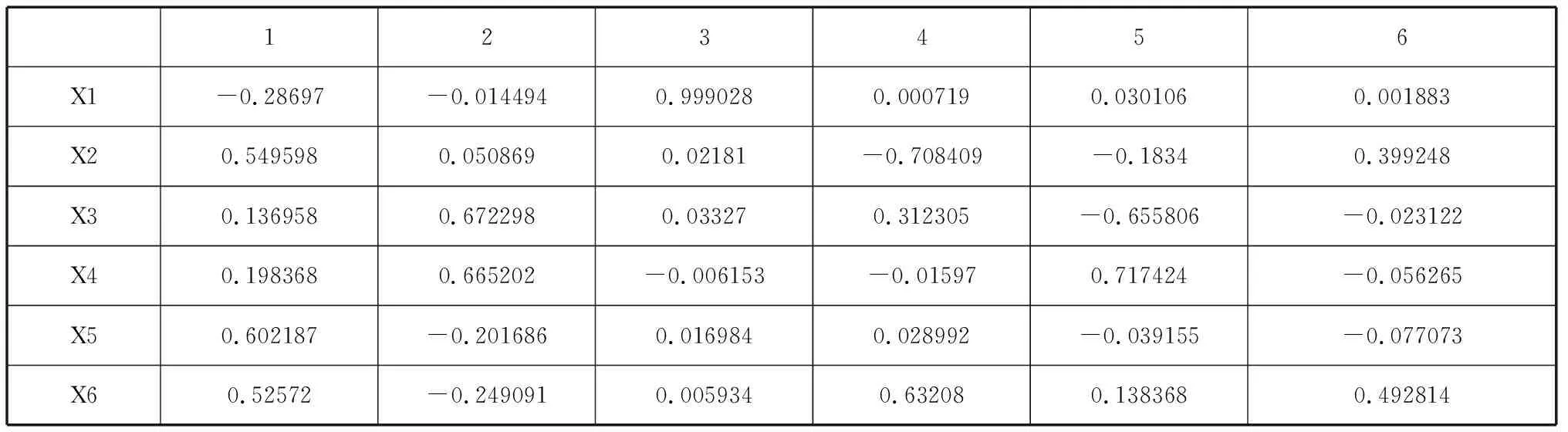
表4 主成分得分

求主成分的因子载荷矩阵，确定主成分与变量间的表对载荷矩阵的第i列的每个元素分别除以第i个特征根的平方根，就得到主成分分析的第 i个主成分的系数，由此得到前3个主成分X1、X2、X3的线性组合为(X为标准化后的变量)。把系数和相应的指标相乘后再求和，可以得到最终的主成分的分公式：

F1=-0.287X1+0.550X2+0.137X3+0.198X4+0.602X5+0.526X6

F2=-0.014X1+0.051X2+0.672X3+0.665VBX4-0.202X5-0.249X6

F3=0.999X1+0.022X2+0.033X3-0.006X4+0.017X5+0.006X6

本文仅从单纯的数量上考虑，以3个因子的方差贡献率为权数。即：P=0.4F1+0.3F2+0.17F3

2.5 回归模型

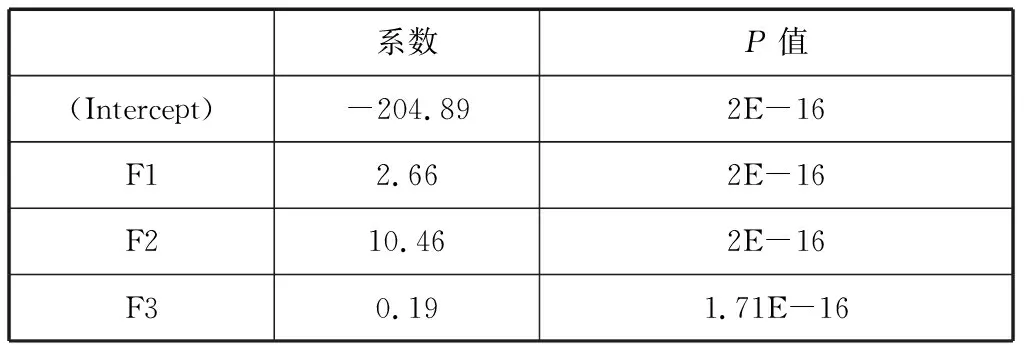
表5 主成分回归

对具有代表性的主成分进行回归分析，从上表5中可以看出F1、F2、F3的P值均小于0.05，且调整后的R2为0.988，得出3个主成分可以表达98.88%的信息，其效果显著，F1、F2、F3的回归关系式为：Y=204.89+2.66F1+10.46F2+0.19F3

采用逆变换法，运用代码求原回归模型，最终求得回归方程为：Y=226.43+55.47X1-0.85X2-8.65X3-7.53X4+0.27X5+0.54X6

3 结语

本文通过主成分回归分析得出，左下拉杆铰接点、左下拉杆倾角、右下拉杆倾角与耕深成正比例，右下拉杆铰接点、左下拉杆、右下拉杆与耕深成反比例。在农田地表温度、酸碱度特定的条件下，耕深的深度决定粮食的产量。因此，在未来的农田耕种中，可以通过给定的变量值不断试验耕深，以求达到粮食产量的增加。