一种度修正的属性网络随机块模型

郑忆美 贾彩燕 常振海 李轩涯

1(北京交通大学计算机与信息技术学院 北京 100044)2(交通数据分析与挖掘北京市重点实验室(北京交通大学) 北京 100044)3(天水师范学院数学与统计学院 甘肃天水 741000)4(百度在线网络技术(北京)有限公司 北京 100085)(ymzheng@bjtu.edu.cn)

现实世界中各种各样的人、物及二者之间的联系构成了诸多复杂系统，这些复杂系统常常以复杂网络的形式进行刻画.其中，网络中的节点表示数据对象，节点之间的边(节点链接)表示数据对象之间的关系，节点度的大小表示对象与网络中其他对象的交互紧密程度.社交关系网络、蛋白质交互网络、文献引用网络等都是复杂网络的典型代表.

人以类聚、物以群分，复杂网络中同样存在着聚集现象，常被描述为社区结构.依据网络的拓扑关系，网络中社区结构表现为：社区内部节点连接紧密、而社区之间节点连接相对稀疏[1].这种结构也常被称为同配结构，它具有度大的节点倾向于与网络中其他度大的节点相连的性质.

在现实世界中，网络中不仅存在上述传统的社区结构，也存在其他类型的结构，如与社区结构相对的子图内连接稀疏而子图间连接相对紧密的二部图结构.以英文文章中名词形容词搭配网络为例，名词和形容词分别构成二部图中的一个子图(社区)，由于名词、形容词之间经常搭配出现，而很少自身相邻，因此2个子图间往往存在更多的边.与同配结构相对，我们称二部图结构为异配结构(可简单理解为违背同配结构原理的其他类型网络结构).除此之外，星形结构、核心-外围结构、混合结构等都是异配结构的典型代表[2].本文，我们将同配结构及异配结构统称为广义结构.

现有许多传统社区检测方法仅针对典型社区结构进行，而对真实世界中的网络，我们往往事先未知网络中潜在的结构.因此，不限定网络结构的类型，检测不同类型网络中的广义结构具有重要的理论和现实意义.如社交关系网络中基于用户兴趣群体检测进行产品推荐、互联网中网页主题预测、蛋白质交互网络中蛋白质功能分析等.现有的社区检测方法依据目标函数的不同可以分为：启发式方法和基于概率模型的生成式方法.

典型的启发式方法主要包括：基于模块度优化的FN算法[3]、Louvain算法[4]；基于图分割的KL算法[5]、归一化割算法[6]；基于非负矩阵分解的BIGCLAM算法[7]；最小描述长度优化方法Infomap[8]以及最近的多目标演化聚类方法[9]等.这些方法的共同特点是：利用对社区的直观经验假设和机器学习中的聚类模型设计度量函数，进而找到近似最优解，一般适用于发现网络中的经典社区结构.

基于随机块模型的概率生成式方法，包括SBM[10]，NMM[11]和DCSBM[12]等.这类方法利用网络拓扑关系将网络中的社区分布建模为隐变量，将实际网络看成以社区分布为隐变量的概率生成过程，从而通过最大化似然函数求解网络结构.与文本分析中的主题模型(如PLSA[13]，LDA[14]等)类似，该类方法具有较好的可解释性，数学形式优美.同时由于随机块模型的性质，该类方法可以用于检测相对于经典社区结构更一般的广义结构，受到了人们的关注.

以上模型都只利用了网络中链接反映的拓扑结构，然而，真实网络中的节点间除了存在链接关系，节点本身还具有描述自身特性的属性信息.如社交网络中，对用户的性别、年龄、学历等的描述，本文将节点含有属性信息的网络简称为属性网络.在属性网络中，网络节点间的关系可能就是因为节点属性信息的相似性诱导的.如具有相同兴趣且物理地址比较接近的人与人之间更容易形成朋友关系；具有相同研究兴趣的学者更有可能在作者合作网络中形成边.因此，网络的链接关系和节点的属性信息之间可能具有一定的一致性和互补性，单纯利用一方面的信息会忽略另一方面的影响.已有研究证明：节点属性信息不但有助于提高网络社区检测的准确度，还可以帮助我们更好地理解网络中存在的结构，对检测到的网络结构提供更好的可解释性[15].

目前越来越多的生成式方法也逐渐面向属性网络展开.主要有：PCL_DC[16]，CESNA[17]，PPSB_DC[18]及NEMBP[19]等.其中，PCL_DC和CESNA是面向经典社区结构而设计的，对于网络中的其他异配结构检测适应性较差.同时，PCL_DC和PPSB_DC采用了两阶段投影求解方法，我们发现这种求解策略不能保证算法的收敛性[20].而NEMBP学习节点社区与属性隐含主题之间的关系，需要同时给出网络中隐含的社区个数和属性主题个数，且相关研究在实验中假设二者一致，缺乏广泛性.

针对以上问题，我们给出了一种融合节点属性与网络拓扑信息的生成模型PSB_PG[20].该模型可以检测网络中的广义结构，且在模型参数求解过程中使用了期望最大化(expectation-maximization, EM)算法[21]，具有较好的收敛性.同时该模型只关心社区与节点属性的关系，允许一个社区中含有多个属性主题，具有较好的灵活性.但PSB_PG模型在生成过程中没有考虑真实网络中节点度的幂律分布规律，不能准确地反映观测网络的结构.因此，本文在其基础上提出了一种度修正的属性网络随机块模型DPSB_PG，结合节点度信息更好地拟合真实网络.

DPSB_PG根据随机块模型中的块结构假设和节点属性的稀疏性假设，令节点之间的链接关系和节点属性的产生都服从泊松分布，但彼此之间独立(即独立同分布).同时隐含假设节点的“社区结构”归属度和节点属性的“主题”归属度共享隐变量，进而将链接与属性隐性相关联.并且，我们在该模型中引入了节点的度，通常具有较大度的节点更倾向于与其他节点相连，进而以一定概率影响网络链接的生成.该模型可以反映现实世界中节点度的幂律分布，具有更好的数据拟合能力、可解释强.最后，我们采用EM算法[21]推断模型参数，保证了模型求解过程的收敛性.与已有同类方法及PSB_PG模型在多个真实网络上的实验对比显示：所给方法DPSB_PG不但保持了PSB_PG的良好性能：适用于广义结构检测、收敛性好、可解释性强等，且相对于PSB_PG等其他方法在性能上有一定程度的提升，不仅能应用于属性网络社区检测，针对非属性网络也具有良好的适用性.

1 相关工作

1.1 基于生成式模型的网络结构检测

真实网络中节点之间的链接关系是对网络拓扑结构最直观的反映.近年来，有大量的算法仅通过利用网络中拓扑关系发现其中的“社区”.

2007年Newman等人首先提出了混合模型NMM(Newman mixture model)[11]，在给定社区数目的情况下，对观测网络中链接的生成构建概率模型，通过最大化似然函数，得到节点所在的社区.该模型定义了节点对社区的隶属度，其思想被广泛应用于之后的生成式方法中.同时模拟从某个“社区”中的节点向其他节点(可以来自当前“社区”，也可以来自其他“社区”)发边的概率构建网络，具有识别广义结构的能力.

随机块模型(stochastic block model, SBM)[10]是近年来生成式方法中的主流模型.该模型定义了节点所在社区间连边的概率，其中边的数量的产生服从泊松分布，进而生成网络.由于块结构假设：2个结构间有边的概率不受节点间差异的影响，只与结构块有关.因此该类方法可以根据随机块矩阵中对角线与非对角线元素的大小识别网络中多种不同的结构.但由于其中忽略了节点的异质度信息，可能导致与真实网络不符.2011年Karrer和Newman在标准SBM的基础上引入了节点期望度对网络生成过程进行了控制，改善了SBM对真实网络的拟合效果.并根据节点之间连边服从泊松分布，设计得到度修正随机块模型(degree corrected stochastic block model, DCSBM)[12]，利用基于贪心策略的社区标签交换思想最大化目标函数，对网络中社区进行刻画.

除对随机块模型中加入节点度信息进行修正外，许多随机块模型的扩展方法相继被提出.如将节点的混合隶属度与随机块模型结合，设计得到MMSB(mixed membership stochastic blockmodel)模型[22]，以检测网络中的重叠社区.2011年Shen等人提出广义随机块模型(general stochastic blockmodel, GSB)[23].该模型假设网络中产生一条边的概率与边的2个端点所在的社区及社区间的连接概率有关.同时，模型结合最小描述长度原则(minimal description length principle, MDL)[24]解决了网络中社区数量选择的问题，其提出使得对网络没有过多先验知识情况下也能发现多种网络结构.

1.2 基于生成式模型的属性网络社区检测

属性网络中，除了网络中链接关系能反映社区结构或其他结构外，节点属性也体现出一定的簇或主题结构.这2种结构具有一定的一致性和互补性，同时利用这2种信息，能够设计更有效的属性网络社区检测算法.最近提出的Metacode算法[25]，虽然没有完全利用节点属性信息提高社区检测的性能，但其也进一步证明了社区结构与属性的相关性，推动了属性网络社区检测的进展.

2009年Yang等人认为节点之间的连边不仅与尾节点所在社区有关，同时也受节点流行度的影响，即尾节点流行度越大，越容易被节点连接，进而对网络中边的产生过程进行建模得到PCL(popularity-based conditional link)模型.进一步，在其基础上引入内容判别模型(discriminative content model, DC)对节点内容进行逻辑回归分析，通过共享社区和内容主题隶属度将链接的生成过程与节点内容主题的回归分析过程线性加和，构建了生成模型PCL_DC[16].最后，利用两阶段投影算法对模型求解.但该模型只考虑了尾节点的流行度对网络生成过程的影响，且较适用于发现传统社区结构，对网络中含有二部图、混合结构等其他异配结构的社区检测问题适应性较差.

为了解决PCL模型中只考虑一种类型边的情况，2010年Yang在其模型基础上针对有向网络引入节点流行度和生成度，即同时考虑了节点被其他节点连接构成边以及连接其他节点进而构成边2种情况，提出了生成模型PPL(popularity and productivity link model)[26].该方法更加充分地考虑了网络拓扑结构，但同样只适合于检测网络中的传统社区结构.

之后，Chai等人继承PPL模型和GSB模型的优点，结合DC模型构建了PPSB_DC模型[18].该模型不仅考虑了节点度的幂律分布，也融合了节点的属性信息.为解决PCL_DC只能识别传统社区结构的弊端，模型采用了GSB中的块结构假设，可以识别网络中广义结构.在模型参数求解中，PPSB_DC同样使用了与PCL_DC类似的两阶段投影算法.但近期研究发现[20]：这种两阶段算法不能保证收敛.

Chen等人2016年在贝叶斯框架下提出了融合节点链接与属性的概率模型BNPA(Bayesian nonparametric attribute model)[27]，以解决社区数量的定义问题.该模型在NMM模型的基础上引入社区中节点含有属性的概率，与节点连边共同构成生成式模型.其继承了NMM模型的优点，因此能发现网络中存在的广义社区结构.并且，该模型利用非参数贝叶斯方法引入先验信息CRP(Chinese restaurant process)[28]对社区数量进行推断，在一定程度上解决了大多数方法需要预先定义社区数量的问题.但其可能对网络社区数量推断不准确，进而影响广义结构识别的精度.

近两年，He等人为进一步探究社区的语义关系，将网络拓扑与节点内容联合建模来刻画社区及社区相关的属性语义，构建了NEMBP(nested EM algorithm with belief propagation)模型[19].该模型假设社区和属性主题共享潜在的类结构，对二者之间的关系进行刻画，同时结合度修正以及多项式分布对边和属性的生成过程进行建模，更好地拟合了真实网络.最后，利用BP(belief propagation)[29]算法和嵌套EM算法对模型参数进行求解.相对单层EM算法，NEMBP模型求解复杂度较高.同样，该模型可以识别网络中的广义结构，但是由于模型对属性主题的刻画，其需要预先给定社区和内容主题个数，并在实现过程中假设二者一致，而这往往与真实网络不符.

2 DPSB_PG模型

在对网络进行社区检测的过程中融入节点属性信息可以在一定程度上改善对网络的理解.近期我们针对属性网络提出了PSB_PG模型[20]，从融合节点属性与链接的角度出发，根据二者之间的潜在关系构建生成式模型.然而，由于真实网络具有无标度特性，其中节点的度分布符合幂律分布.因此各节点的链接情况(节点度数)分布不均匀，一般地，节点的度越大，越倾向于与其他节点相连接.近年来，相关社区检测算法也逐渐将节点度相关的变量引入网络生成过程中，以更加准确地拟合真实网络.

本文主要考虑了节点度对节点间连边的影响，以进一步提高模型对观测网络的拟合能力，进而构建了属性网络中含有节点度信息的度修正随机块模型DPSB_PG.该模型中网络结构与节点属性的生成均服从泊松分布，且二者相互独立.值得注意的是，本文的DPSB_PG模型是对PSB_PG模型的扩展，其主要差别在于是否引入节点度这一可观测变量，并在实验过程中对模型的性能进一步分析.本节我们直接介绍DPSB_PG模型，第3节我们将介绍其EM算法求解过程，并在第4节对实验进行完善，不仅证明了此改进模型度修正信息引入的有效性，同时对不同的网络(网络中是否考虑节点属性信息)进一步比较，证明了该模型的可扩展性.

2.1 问题定义

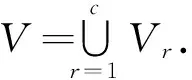
为清晰理解模型中各符号的意义，表1展示了模型中的主要参数.

Table 1 Symbol Description of the DPSB_PG Model表1 模型部分符号说明

2.2 节点链接生成过程

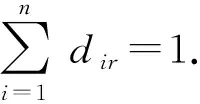
因此，网络中任意节点对(i,j)之间是否存在边不仅与节点的社区隶属度D、社区间连接概率矩阵Θ有关，同时受节点度的影响.通过节点度对网络生成过程进行控制，可以更好地拟合真实情况.这里，假设节点对(i,j)间边的生成是独立的且服从泊松分布，可以得到节点对(i,j)之间生成一条边的期望为

其中：

满足归一化约束.

与度修正随机块模型DCSBM[12]相对应，我们允许生成网络中包含多边和自环现象.因此，根据泊松分布过程，当给定参数D，Θ及观测变量xi后，生成网络G的概率P(A|D,Θ)为

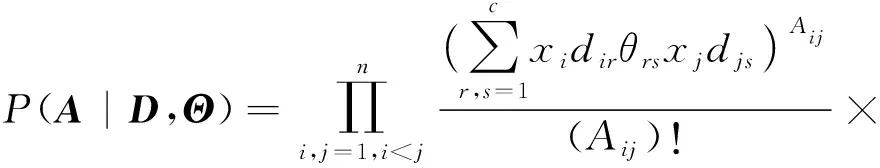
(1)

以上网络链接的生成过程中结合节点度信息进一步利用了网络的拓扑结构，对真实网络结构充分拟合.其中，随机块矩阵Θ可以对网络中隐含的结构类型给出直观的解释.当其主对角线元素大且非对角线元素小时，网络呈现传统社区结构；当主对角线元素小且非对角线元素大时，对应社区内连接相对稀疏，社区间连接紧密的二部图结构；其他一般情况可对应于混合社区结构.因此，本模型能在生成过程中对网络中隐含的结构类型进行判断，具有识别网络中广义结构的能力.同时，网络中节点可能属于一个或多个社区，而隶属度矩阵D可以反映出节点社区的分布情况，可用于识别重叠社区(隶属度以dir为阈值指派)或非重叠社区(隶属度最大指派)，PSB_PG中对重叠社区检测能力进行了比较[20]，本文重点针对非重叠社区进行实验.

2.3 节点属性生成过程

针对属性网络，通常网络中每个节点对应的属性往往是高维的，而对于一个社区而言，其中的节点是否含有公共属性具有稀疏性.若一个社区中节点的属性高度相关，也会与网络拓扑结构一致或互补，进而促进社区的构成.因此，我们假设社区中节点属性的生成同样服从泊松分布.

设φrk表示社区Vr含有属性k的概率，并构成社区相关属性矩阵Φ=(φrk)c×K.显然，社区内所含有的属性信息可以为相关社区提供丰富的语义解释，挖掘其中的主题分布.类似地，网络中节点i具有属性k与节点度xi、社区隶属度D以及社区相关属性Φ有关，则期望为

且满足归一化约束：

因此根据泊松分布过程，在给定参数矩阵D，Φ后，网络中生成节点属性的概率P(W|D,Φ)为

P(W|D,Φ)=

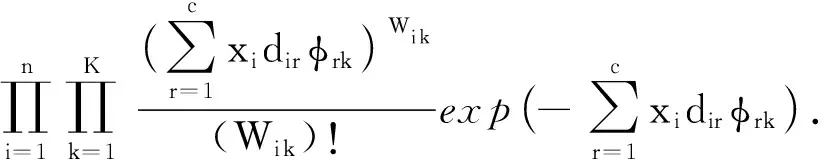
2.4 融合节点属性的网络生成过程

设社区属性隶属度与节点社区隶属度共享网络中的潜在社区，以便对二者之间隐含联系进行刻画.假设网络中节点邻接矩阵A与属性矩阵W生成过程彼此独立，则融合度修正信息的属性网络随机块模型DPSB_PG的联合分布形式表示为

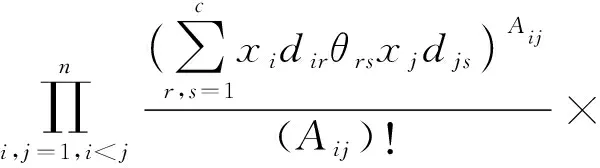
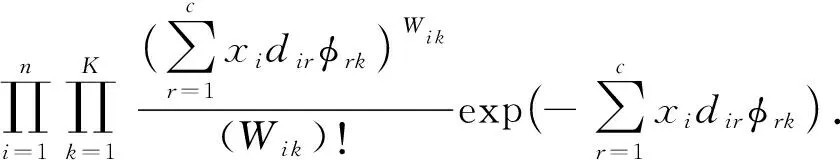
相应地，网络中的链接和节点属性的生成过程可总结为：

1) 以概率dir从社区Vr中抽取一个节点i且以概率djs从社区Vs中抽取一个节点j；

2) 以概率为节点对(i,j)生成一条边：

3) 以概率φrk在社区Vr中选择一个属性k；

4) 以概率为节点i选择一个属性k：

对应概率图模型如图1所示：

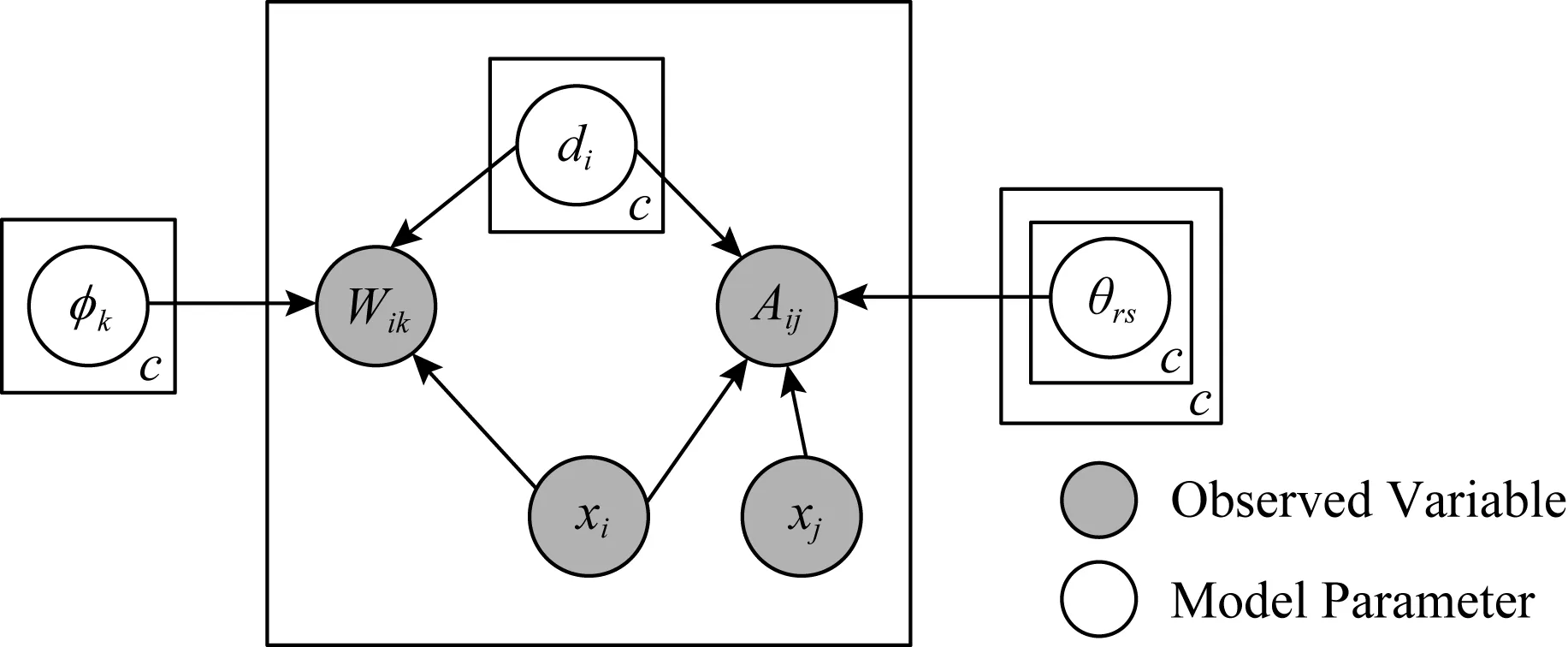
Fig. 1 The probabilistic graph model for DPSB_PG图1 DPSB_PG概率图模型

3 DPSB_PG模型EM求解算法

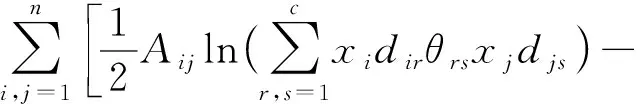
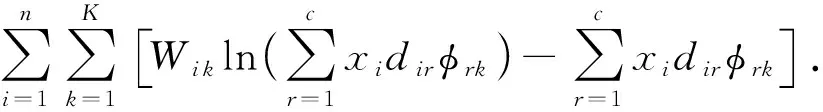
然而，由于式(4)难以直接计算,因此本文利用处理这类问题常用的EM算法[21]求解.EM算法能保证收敛到模型的局部最大值，从而获得模型最优参数.

根据Jensen不等式E[f(X)]≥f(EX)(f为凸函数，当且仅当X为常数时等式成立)可得到对数似然的下界：

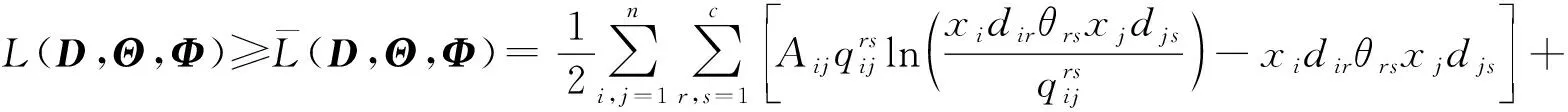
(5)

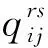
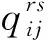
(6)

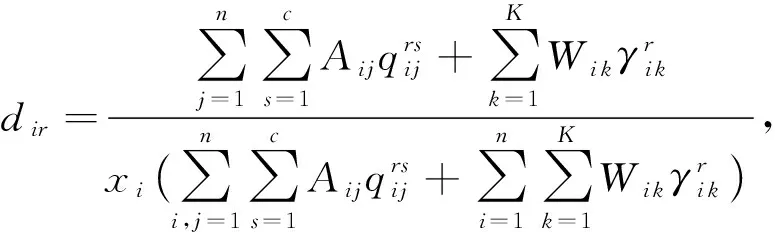
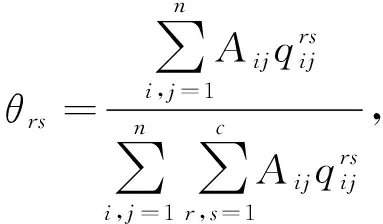
(9)

首先，随机初始化参数D,Θ,Φ，然后重复迭代EM算法，对式(6)和式(7)～(9)不断更新直至目标函数收敛或达到最大迭代次数，输出对应的模型参数D,Θ,Φ，对应最优的网络拟合效果，具体算法过程见算法1.因此，可以通过该算法挖掘网络中节点的社区分布情况，社区对应的属性分布以及网络中广义社区结构.由于EM算法求解过程，上述参数的形式看起来与PSB_PG中参数结果相差不多，这也表明概率生成模型数学形式的优美.但实质上，节点度xi的引入直观影响了节点所在的社区分布，同时由于潜变量的变化，会间接影响社区属性以及网络结构的推断，因此相较于原PSB_PG算法仍具有一定程度的变化.

算法1.DPSB_PG模型算法.

输入：邻接矩阵A、属性矩阵W、社区数量c、最大迭代次数IT和阈值ε;

输出：模型参数D,Θ,Φ.

① 由邻接矩阵A计算每个节点i的度xi;

② 随机初始化模型参数D(0),Θ(0),Φ(0);

③ fort=1:ITdo

⑤ M步：根据式(7)～(9)分别更新模型参数D(t),Θ(t),Φ(t);

⑥ ift=IT或者|L(t)-L(t-1)|<εthen

⑦D=D(t),Θ=Θ(t),Φ=Φ(t)；

⑧ break；

⑨ end if

⑩ end for

由于社区隶属度矩阵D刻画了每个节点i在所有c个社区上的分布，基于此可以推断网络中节点的社区归属度，可以是软划分(即通过限定dir的阈值，超过此阈值时一个节点可以归属于对应的多个社区)，也可以是硬划分(即只利用dir的最大值，限定一个节点只能归属于一个社区)，分别对重叠社区或非重叠社区检测，本文主要针对非重叠社区检测进行.随机块矩阵Θ反映了网络中存在的结构类型，可以根据其对角分布推断其是经典社区结构、还是二部图结构或是混合结构等.社区相关属性矩阵Φ描述了每个社区相关的属性特征，可以通过属性类别分析当前社区的语义，增强所识别社区的可解释性.并且，由于EM算法自身的收敛性质保证了DPSB_PG求解算法的收敛性.

算法1的时间复杂度主要取决于EM算法对参数的更新迭代过程.其中，执行E步的时间复杂度为O(mc2+nKc)，执行M步的时间复杂度为O(nc+c2+nck)，又由于实际网络中社区数量c常小于节点个数n且算法的最大迭代次数是IT，故算法1整体的时间复杂度可为O(IT(mc2+nKc)).

4 实验结果及分析

4.1 评价指标

本文采用常用的标准化互信息(normalized mutual information,NMI)[30]以及F测度(pairwise F-measure,PWF)[16]2种评价指标度量本文模型与现有方法在真实网络上的广义结构识别效果.其分别表示为

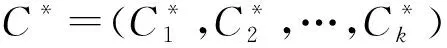
其中，precision=|S∩T|/|S|,recall=|S∩T|/|T|分别表示算法划分结果的精确度和召回率，S表示算法识别社区中具有相同类标的节点集合，T表示对应的真实网络中具有相同类标的节点集合，|·|表示集合中元素数量.

利用NMI,PWF这2种指标对社区划分的质量进行评价可较为直观地表示算法检测到的社区划分与真实划分的差异.其中二者的值介于0和1之间，值越大，表示所对应的社区划分效果越好.

4.2 参数设置

由于节点对(i,j)所对应社区随机块矩阵Θ反映了网络中隐含广义结构的类型.因此其初始值的设置会严重影响算法的收敛速度与社区检测的精度.当Θ的初始值对应的结构与真实的网络结构一致时，算法收敛速度快，检测结果也相对更优；相反当二者完全相反时(如真实结构是二部图，但初始值为传统社区结构)，算法收敛速度很慢，且容易陷入局部最小.因此，在实验过程中，我们利用最大熵以及最大似然的思想对Θ的初始值进行预判.

在矩阵Θ=(θrs)c×c的初始值选择中，我们考虑3种情况：主对角线元素大、非对角线元素大以及所有元素值随机但近乎相等.这3种情况分别对应：社区结构、二部图结构以及混合结构.因此针对每个网络我们首先对3种初值迭代固定的少量几步(如10步)EM并反复几次，根据式(5)计算多次的平均似然值.最后选择3种情形中平均似然最大时对应的Θ情况作为Θ的初始设置.

在实验过程中，我们设置社区数量c与已知的实际网络社区数量相等，同时不限定真实网络的结构类型，对输入的网络通过上述初始化步骤进行网络结构的预判，进而执行对网络社区结构的检测.

4.3 数据集描述

我们将本模型在真实属性网络与非属性网络上进行了实验.表2、表3分别描述了本文所选用的4个真实属性网络数据集和6个非属性网络数据集的相关统计特征.

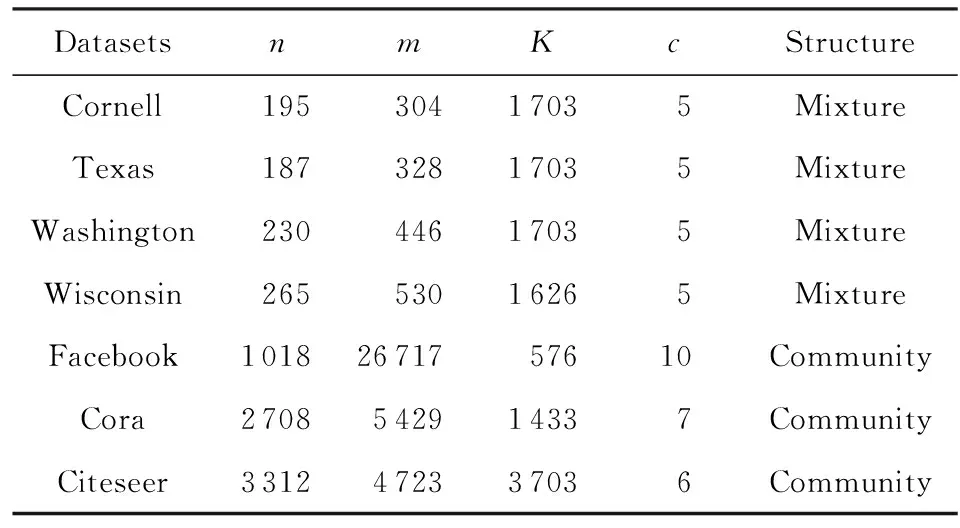
Table 2 Feature of the Attributed Networks表2 属性网络数据集特征

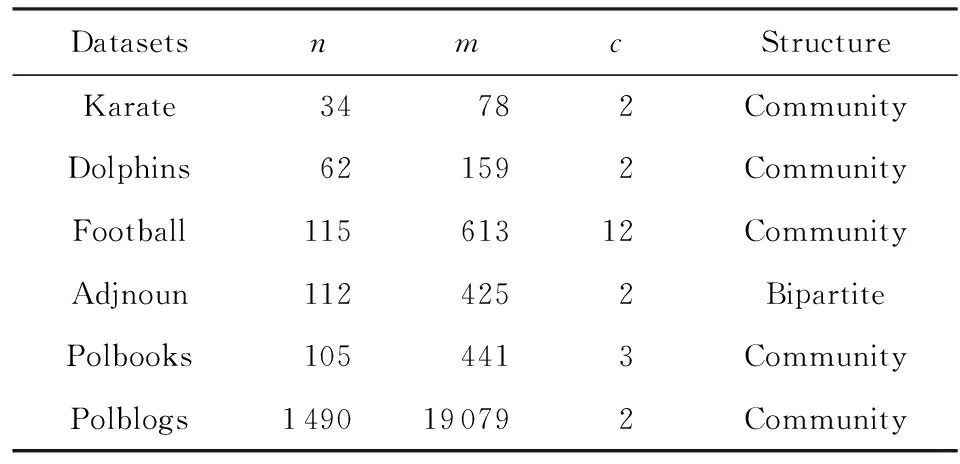
Table 3 Feature of the Non-attributed Networks表3 非属性网络数据集特征

4个属性网络数据集包括：

1) WebKB数据集(1)http://www.cs.cmu.edu/～webkb/.该数据集由Cornell，Texas，Washington，Wisconsin四所大学的网页以及网页间的链接关系构成，共包含877个节点，1 608条边，均划分为5个社区.同时，每个节点都关联一个高维的二值属性特征，由各网页中出现的不同词构成.该数据集的4个网络含有的结构均为混合结构.

2) Facebook数据集(2)http://snap.stanford.edu/data/.该数据集记录了社交网站Facebook上从2005年起的社交关系数据.这里选取其中一个数据子集，包含1 018个节点用户，26 717条边表示了用户之间的朋友关系，同时每个节点由一个576维的属性特征向量描述.

3) Cora数据集[31].该数据集为科技文献引文网络的一个子集，其中包含2 708个节点，代表所有的文献，5 429条边代表文献之间的引用关系，共包括7种文献类别构成的相应社区，同时每个节点都关联一个1 433维的属性向量.

4) Citeseer数据集[32].该数据集也是科技文献引文网络的一个子集，含有3 312个节点，4 732条引用关系，包括6个文献类别构成的相应社区，同时每个节点由一个3 703维的属性向量构成.

6个非属性网络数据集包括：

1) Karate数据集[33].该数据集是一所美国大学空手道俱乐部成员构成的关系网络，包含34个节点和78条边，由于内部矛盾分裂为2个社区.

2) Dolphins数据集[34].该数据集由新西兰某海峡62只海豚群体的交流情况得到，海豚之间的频繁交流构成了网络中159条边，分为2个社区.

3) Football数据集[1].该数据集是由美国大学生足球联赛构建的网络，包含115个节点和613条边，其中节点表示各个足球队，边表示两球队之间进行过比赛，所有代表队分为12个联盟.

4) Adjnoun数据集[35].该数据集表示了某英文文章中形容词与名词的连接情况.共包含名词、形容词构成的112个顶点和表示二者相邻情况的425条边，由于形容词与名词大体上总是相邻出现而很少有名词与名词、形容词与形容词相邻的情况，因此构成了典型的二部图网络结构.

5) Polbooks数据集(3)http://www-personal.umich.edu/～mejn/netdata/：该数据集由关于美国政治的图书在线购买情况构成，包含105个在线商家销售的书籍构成的节点，节点之间共441条连边，表示同一买家频繁购买的书籍之间的关系，构成3个社区.

6) Polblogs数据集[36]：该数据集是由政治博客构成的网络，包含1 490个节点和19 079条边.节点代表网页博客，每条边代表网页间超链接情况，原数据中节点包含了网页政治倾向，代表了2个社区.

4.4 实验结果对比

本节我们通过与相关工作中的提到的部分融合节点属性的属性网络社区检测方法以及只利用网络结构的社区检测方法分别在属性网络以及非属性网络上进行对比实验，以验证本文方法的有效性.

4.4.1 属性网络结果分析

在真实属性网络数据集上，我们将本文的模型DPSB_PG与现有融合节点链接与属性的生成式模型NEMBP，BNPA，PPSB_DC，PCL_DC以及未改进的PSB_PG模型进行了对比实验.为了保持公平，所有比较算法均采用原文中提及的最优参数设置.表4、表5展示了对应的NMI，PWF结果.由于EM算法迭代过程会根据初始值的不同收敛到局部最优解，我们对每个模型进行了30轮实验，并报告了2个指标30轮的均值以及最大值.

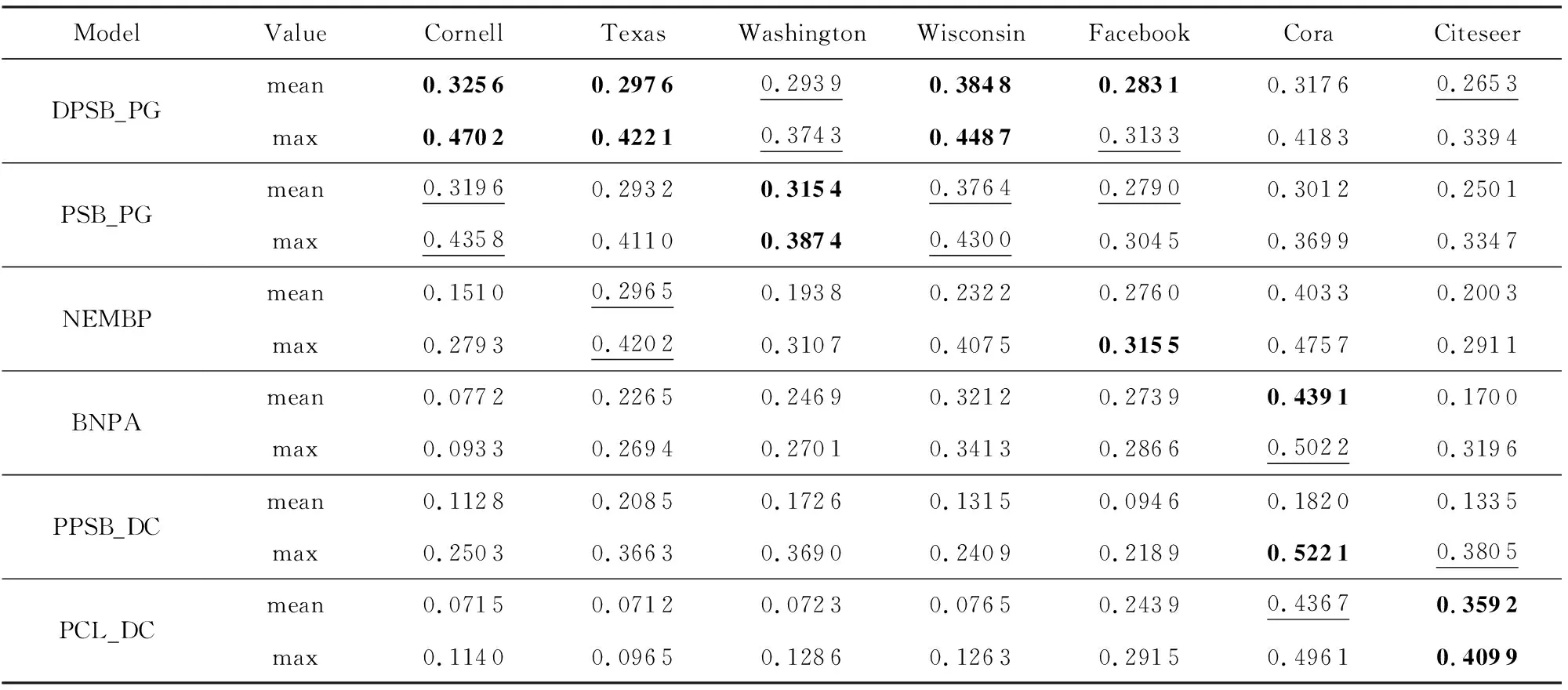
Table 4 Comparison of NMI for Attributed Networks表4 属性网络NMI结果对比

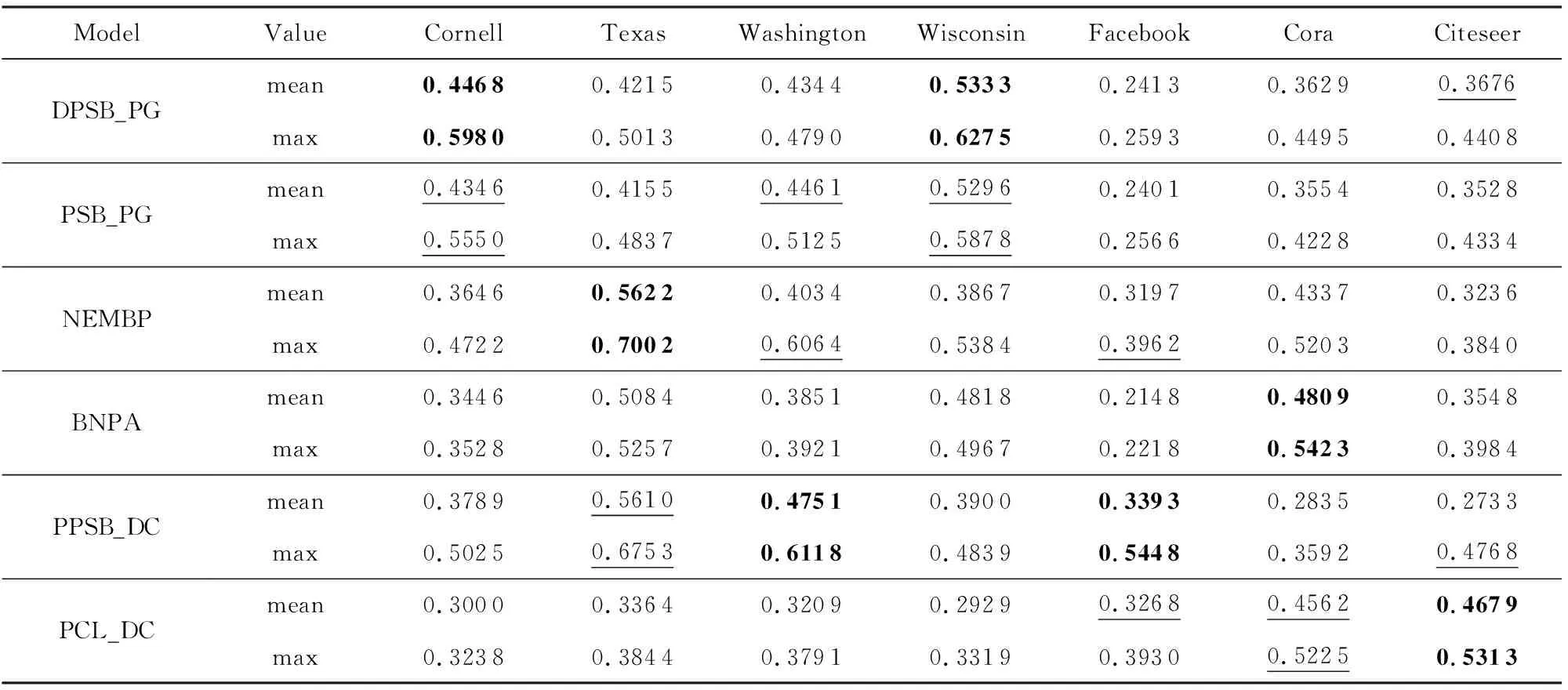
Table 5 Comparison of PWF for Attributed Networks表5 属性网络PWF结果对比

由表4和表5可知：本文提出的DPSB_PG模型可以适用于广义结构检测，且对于含有混合结构的真实属性网络(WebKB数据集的4个网络上)的检测效果有明显改善.相较于没有考虑节点度信息的PSB_PG模型，除在属性网络Washington上表现略差外，我们改进的模型在其他网络中表现更好.说明融入节点的度信息对网络社区结构的检测具有积极影响，使得DPSB_PG模型对数据具有较好的拟合能力.对Washington网络，我们分析发现：该网络规模相对较小，而其中存在多个孤立节点，因此这些节点的度分布可能会影响本模型的整体表现，相较于未引入度信息的PSB_PG模型表现略差.

BNPA模型对Cora数据集中社区结构的检测得到了最好的效果，但由于其引入了先验信息，需要对先验参数进行调参，且其检测精度依赖于社区数量估计的准确性，在其他网络中表现效果不佳.PCL_DC模型在具有社区结构的Cora，Citeseer网络上取得了较好的效果，但对非传统社区结构适应性较差.进一步，我们的模型在Citeseer中表现仅次于PCL_DC，由指标NMI可知，在Facebook数据中表现最优，这也说明本模型在混合结构、社区结构网络中均表现出良好的性能，而NEMBP，PPSB_DC模型在各个网络中的表现具有不稳定性，NEMBP仅在Texas网络中取得了较好的效果，PPSB_DC由于初值及收敛性的影响使得表现效果差异较大.因此，本文的DPSB_PG模型综合性能优于其他相关算法，说明利用度修正思想以及泊松分布随机块模型能较好地识别属性网络的广义结构.

4.4.2 非属性网络结果分析

原PSB_PG模型中重点针对属性网络，对节点属性进行了充分分析，但对非属性网络中模型的表现缺少进一步比较.因此，对模型改进后，在非属性网络数据集中，我们对比了DPSB_PG与其他模型PSB_PG，BNPA-link，PPSB和PCL在只利用网络拓扑信息时性能上的差异(同样所有比较算法均采用原文中的最优参数设置).除此之外，我们的模型在生成过程中引入了节点度修正的思想，与DCSBM[12]模型类似.而二者差异之处在于：DPSB_PG模型采用EM算法求解模型参数，DCSBM模型基于贪心算法利用标签交换思想最大化似然函数求解模型参数.因此，我们也将改进的模型与DCSBM模型进行了对比，以验证本文算法的性能.同样，我们将对比的前4个模型执行30轮并报告了NMI，PWF指标的均值以及最大值.为了与原文保持一致，对于DCSBM模型，我们基于贪心策略执行20次KL算法以实现标签转换，并报告其最大值.为保持公平，我们在与DCSBM对比时只将其与其他模型的最大值进行对比.表6、表7中展示了相应的实验结果.

由表6和表7中结果可知，改进后的DPSB_PG模型在其中4个非属性网络中取得了第1或第2的表现效果，进一步表明我们的模型在仅利用网络拓扑信息时同样能较好地挖掘网络的多种类型结构.在PSB_PG的基础上引入节点度信息进行修正后，除在Adjnoun数据集上DPSB_PG效果略差外，在其他真实非属性网络中的效果均优于PSB_PG模型，可见度修正的引入起到了积极作用，进一步对网络拓扑结构进行了拟合.对Adjnoun网络，我们同样分析发现：在其网络规模下，孤立节点占据较大比重，因此其度分布可能会影响网络链接生成过程，相较于未引入度修正信息的PSB_PG模型性能略有下降.

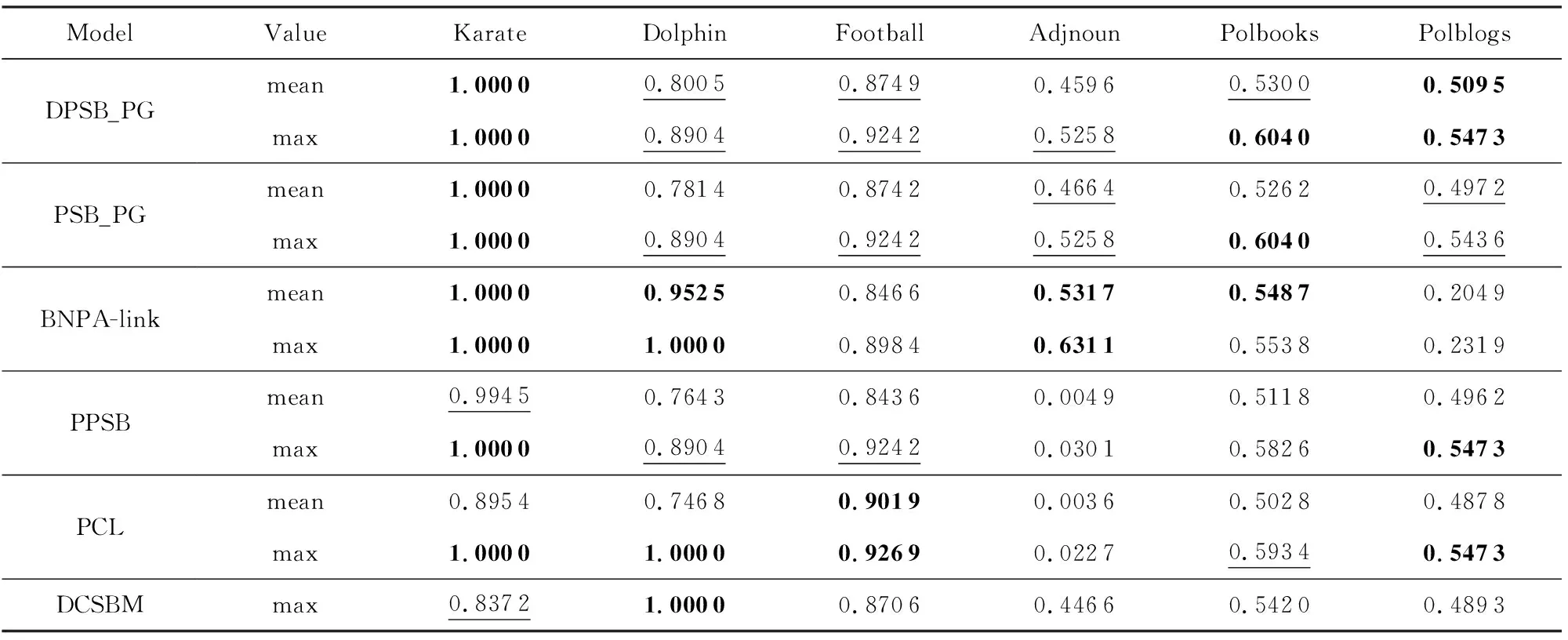
Table 6 Comparison of NMI for Non-attributed Networks 表6 非属性网络NMI结果对比

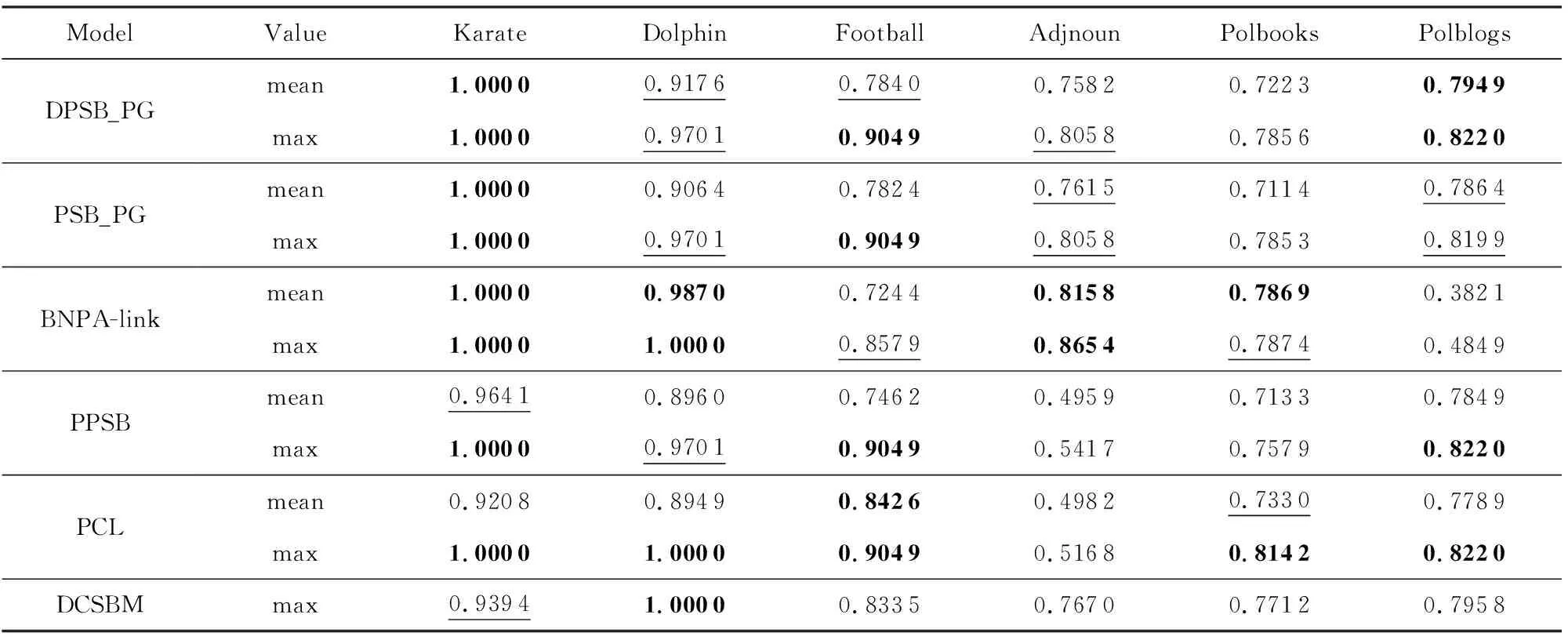
Table 7 Comparison of PWF for Non-Attributed Networks表7 非属性网络PWF结果对比

同样，由于BNPA模型在生成过程中引入了先验，通过对参数的调整可得到相对更优的社区检测结果，因此在Karate，Dolphin，Adjnoun，Polbooks数据集中都取得了最好的效果.但由文献[37]可知，BNPA模型在自动判断社区数量时，与真实网络社区数量差异明显.更一般的情况下，我们的模型效果明显好于PPSB以及PCL模型(除Football网络数据集外).因PCL模型只适用于传统的社区结构，在明显的二部图结构网络Adjnoun中该模型并不适用.对DCSBM模型，其贪心优化策略正确发现了Dolphin网络中社区结构，但对其他网络的检测效果相较于我们的算法较差，在这里标签交换思想没有额外的优势.因此通过对比可以反映出：我们的模型在仅利用节点链接信息时同样对网络中社区结构、二部图结构的检测具有较好的性能.

5 结 论

融合网络中节点之间的链接关系以及节点固有的属性信息挖掘网络中潜在的结构，并利用属性信息增强所识别社区的可解释性，进而揭示网络系统的功能逐渐被人们所重视.本文在PSB_PG模型的基础上引入节点的度信息对模型进行改进，提出了一种属性网络中链接和节点属性产生过程都服从Poisson分布的度修正随机块模型DPSB_PG，以充分拟合节点度在真实世界中的幂律分布特征，并基于随机块特性识别网络中广义社区结构.并且，DPSB_PG模型易于通过EM算法进行求解，具有较好的算法收敛性.通过与现有方法在真实属性网络、非属性网络上的实验比较研究：我们的模型能够发现网络中的广义结构，如传统的社区结构、二部图结构以及混合结构等多种网络结构；节点度的引入更好地拟合了真实网络，因此识别精度优于基础模型PSB_PG，且相较于现有的其他同类算法在性能上也有不同程度的改善.另外，该模型保持了PSB_PG模型灵活的社区语义关系学习特性以及重叠社区检测能力.

由于EM算法在模型参数求解过程中根据网络规模的不同，可能需要较大的计算量，进而影响模型的效率.因此，在今后的工作中，我们拟引入变分推理或随机变分推理等其他策略加快模型参数的求解过程，在保证社区检测精度的基础上提高算法的计算效率，以适应更加大型的复杂网络，更快更好地挖掘网络中的“社区”结构.