基于波文比和降水的综合干旱指数的构建及应用

杜瑞麒，张智韬，巨娟丽，劳聪聪，金继明，崔晨风

(1.西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100；2.西北农林科技大学旱区农业水土工程教育部重点实验室，陕西 杨凌 712100)

0 引 言

干旱是一个机理复杂且致损严重的自然灾害，特别是在全球气候变化背景下，世界各地的干旱事件愈发的频繁[1]。把握干旱动态变化，及时发现旱情，实现对干旱的精准监测，可以为防旱抗旱提供科学依据，提升农业生产水平具有重要意义。

目前的干旱监测方法主要有两大类，一类是基于地面站点的传统干旱监测模型，一类是基于卫星的遥感干旱监测模型[2, 3]。前者主要是依靠气象站点所提供的气象数据来计算出干旱指标，如帕默尔干旱指数PDSI(Palmer Drought Severity Index)[4]、标准降水指数SPI(Standardized Precipitation Index)[5]、相对湿润度指数MI(Moisture Index)[6]、标准蒸散降水指数SPEI(Standardized Precipitation Evapotranspiration Index)[7]，这些指数从反映地面降水，气温，蒸发等气象要素来表达干旱的过程，从而实现对干旱的监测。由于气象站点的数据精度较高，因而可以反映出干旱整个过程变化。但这种方法不仅耗费较大的人力物力，而且只能以站点形式反映信息，无法反映空间异质性，在实现区域化干旱监测上有很大的困难。随着遥感技术的成熟，基于卫星的遥感干旱监测模型凭借空间连续的优势使得大范围干旱监测成为可能。干旱的遥感监测，主要是根据植被形态或植被温度信息来计算相应的指数，如归一化差值植被指数NDVI(Normalized Differential Vegetation Index) 、植被条件指数VCI(Vegetation Condition Index)、温度条件指数TCI(Temperature Condition Index)等[8, 9]，这种方法通过表达植被状况来间接反映出干旱过程中土壤水分状况，从而实现干旱监测[10, 11]。

然而，干旱是多个因素综合到一起的现象，单个指数无法反映干旱过程中的全部特征，使得干旱监测的结果往往具有片面性，因此国内外学者们尝试融合多个干旱变量来构建综合干旱指数。杜灵通等结合NDVI、TCI和TRMM卫星降水数据构建综合干旱指数SDI(synthesized drought index)[12]；任怡等结合PDSI、SPI和SPEI构建综合评价指数DI[13]；张建平等结合MI和NDVI构建综合干旱监测指数DI(comprehensive drought monitoring index)[14]。这些研究表明结合多变量构建干旱指数能够大大提升干旱监测的精度，但要实现区域上的干旱监测，就必须涉及遥感干旱指数。尽管遥感干旱指数都能够间接地反映土壤水分状况，但已有的研究表明，这些指数具有不同的优缺点和适用范围[15, 16]。不同的植被覆盖、地表粗糙度、土壤类型和地形等都会给遥感干旱指数的精度带来很大的不确定性，因此探索新的遥感干旱监测方法对干旱监测研究具有重大意义。

波文比(β)是基于地表能量平衡原理来反映陆地能量分配比例的一个指标[17]。土壤水分的变化会引起地表能量分配情况发生相应的变化，因此波文比可以反映出地表的干湿特性[18]。相比于遥感干旱指数来说，波文比是通过陆地能量分配过程来反映土壤水分状况，不会因地表覆盖差异而有所变化，可以避免遥感干旱指数在监测上的局限性，但在遥感干旱监测领域上却很少涉及[19-26]。

本文将基于波文比构建反映土壤水分的波文比指数SBI，并在此基础上结合标准化降水指数SPI构建出能够反映出土壤水分和降水的综合干旱监测指数MSBP，并以吉林省为研究区域，分析MSBP指数在区域干旱监测上的效果，为农业综合干旱监测及旱灾预警提供一种新的监测指数。

1 材料与方法

1.1 研究区概况

吉林省位于中国东北部，和辽宁、黑龙江、内蒙古接壤相连，地势上呈现出东南高，西北低的特点，地貌主要分为东部的山地和中西部的平原，其概况如图1所示。该区域的气候属于温带大陆性气候，气候特点存在明显的季节和地域差异，从东南向西北，气候由湿润到半湿润再到半干旱，气温年较差在35 ℃以上，年内降水分布不均，主80%集中在夏季。吉林是全国重要的粮食生产基地，根据《2017年国家统计年鉴》，2016 年吉林粮食总产量为4 154 万t，产量仅次于黑龙江和河南省，11个县被列为全国粮食生产百强县，在国家粮食安全体系中承担重要角色。

图1 吉林省概况图Fig 1 Correlation analysis between SBI, SPI and MSBP

1.2 数据来源

1.2.1 气象数据

本文所用到的数据均来自于由美国宇航局、美国海洋和大气局联合开发的全球陆面通化系统GLDAS，所涉及的版本有2.0和2.1，通过这两个版本的数据集可以获取到1948年至今的空间分辨率为0.25°×0.25°的遥感数据(http:∥disc.sci.gsfc.nasa.gov/hydrology/ data-holdings)。本文利用的是GLDAS数据中的降水，感热通量和潜热通量数据，从而可以得到吉林省44个县级地区的降水和波文比，其县级地区的具体名称及编号如表1所示[27]。

1.2.2 粮食产量及受灾数据

吉林省44个县级地区的粮食产量记录来自吉林统计年鉴[28]，受灾率则是通过受灾面积和农作物耕种面积的比值计算得出，这两项记录来自中国统计年鉴，上述所用数据的时间范围均为1988-2017。

1.2.3 标准化降水指数SPI

标准化降水指数(SPI)是1993年由McKee提出用来评估降水所引起的干旱的指数[29]。SPI计算原理是认为降雨的频率分布式符合Gamma分布(Γ分布)，通过Γ分布函数可以求出相应的累积概率，从而可以得到在固定时间内的降水量的累积概率，再通过正态化分布转化得到SPI，并以此制定了相应的干旱等级标准(表2)。通过SPI可以在不同时间尺度(如1月、3月、6月、12月等)表征旱情，本文研究所涉及的SPI为一月尺度。

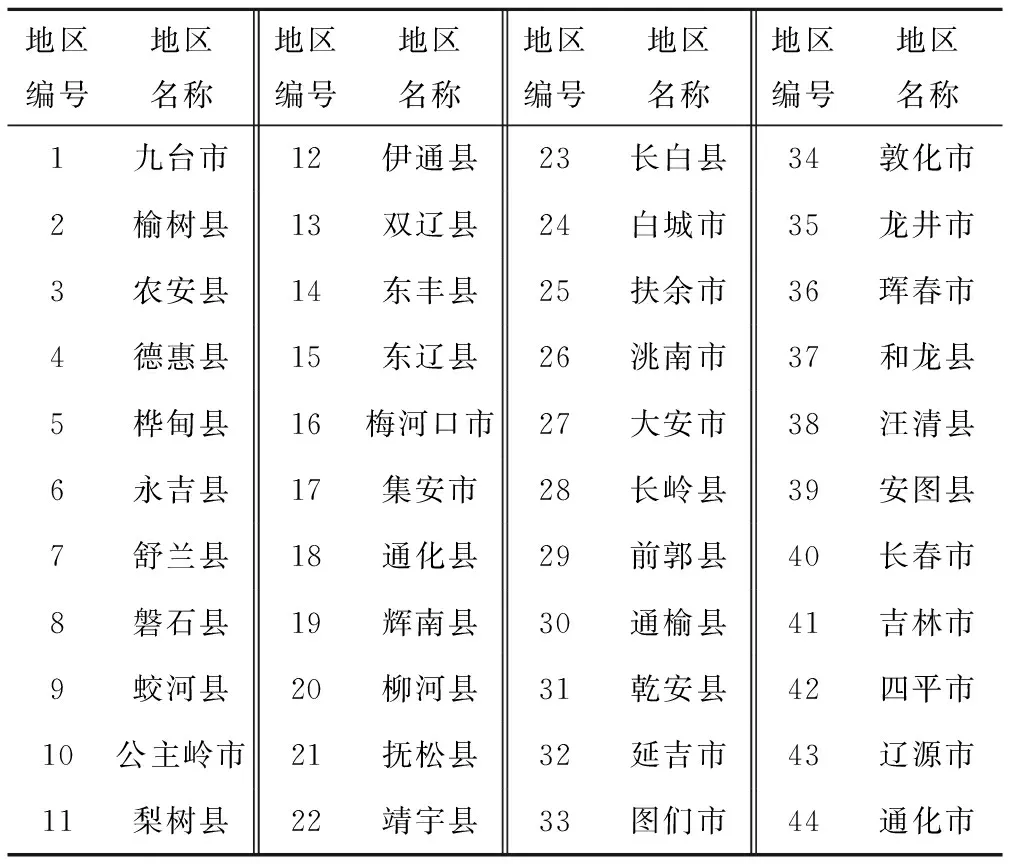
表1 吉林省各个县级地区的名称及编号Tab.1 Names and numbers of counties in Jilin Province

表2 干旱等级标准Tab 2 Classification of SPI drought grade

1.2.4 标准化波文比指数SBI

波文比β可以综合反映地表的水热特征，其计算公式为：

β=H/LE

(1)

式中：H为感热通量；LE为潜热通量。

在计算出月尺度的波文比之后，将历史周期同月份的波文比组成序列并进行GEV分布，Logistic分布，EV分布和Г分布来拟合，各个分布的参数估计用最大似然估计，然后使用K-S方法进行拟合优度检验来确定最适分布函数。为了和SPI干旱等级划分标准相一致，根据确定的最适分布函数，计算出每个波文比对应的累积概率，并进行正态变换和取负值处理，就得到标准化的波文比指数(SBI)，计算过程如下：

P(β≤β0)=G(β0)

(2)

SBI=-φ-1(p)

(3)

式中：G为最适分布函数；φ为标准正态分布。

相比于波文比，经过标准化的SBI可以在不同地区之间来衡量干旱状况，且干旱分级和SPI一致，可以和SPI直接比较干旱监测效果，解决了波文比一直以来在干旱监测上无法直接应用的问题。此外，SBI在时间尺度上和SPI一致，为一个月的尺度。

1.2.5 Copula函数

Copula函数能够构造不同边缘分布的多个变量的联合分布函数。在众多 Copula 家族中，本文选择在水文领域上应用广泛的阿基米德 Copula函数[30]。而在阿基米德Copula函数当中，以 Clayton Copula、 Gumbel Copula 和 Frank Copula 应用最广。本文则根据拟合检验中RMSE最小为原则来进行来选择Copula函数和构建波文比、SPI的联合分布，对于Copula函数的参数估计，则采用最大似然估计。

根据Sklar定理，令F、G分布为随机变量x，y的边缘分布函数，H为联合分布函数，则对∀x，y∈R，有Copula函数C使得：

H(x,y)=C[F(x),G(y)]

(4)

若F、G连续，则C是唯一的。

本文中F和G分别对应-β和SPI。

1.2.6 综合干旱指数MSBP

本文选取波文比(土壤水分状况)和SPI(降水)两个描述干旱特征的变量，为了使波文比和SPI之间呈正相关关系，则先要将波文比进行取负值处理，然后根据K-S方法和最大似然估计的参数估计来分别计算出各自最适分布函数下的边缘分布，采用Copula 函数计算其联合概率分布，从而构建出既能表征土壤水分，又能表征降水的综合干旱指数(MSBP)，其时间尺度为一个月。

X和Y为负值处理后的波文比、SPI的某一数值，假设两随机变量相应的边缘分布分别为F(x)和G(y)，则它们的联合分布P可以用累积联合概率p和Copula函数C表示为：

P(x≤X,y≤Y)=C[F(x),G(y)]=p

(5)

于是，由联合分布函数得到综合干旱指数(MSBP)：

MSBP=φ-1(p)

(6)

1.2.7 干旱特征的评估

为了进一步量化每次干旱事件的特征，本文选取干旱历时(D)，干旱烈度和干旱强度(S)3个指标来评估不同指数的干旱表现。根据干旱划分的等级标准(表2)，当指数值小于0.5时则定义为发生了一次干旱事件，干旱事件所持续的时间则定义为干旱历时(D)。在干旱过程中指数值与临界值的差值则为干旱强度(S)，具体表达如下：

(7)

式中：X为干旱指数值。

干旱烈度则可以表示为：

F=max{|X1|,|X2|,|X3|…|XD|}

(8)

式中：X1,X2,X3,…,XD表示在干旱历时D内下每个月份下对应的干旱指数数值。

1.2.8 粮食产量去趋势处理

粮食产量一般由趋势产量，气候产量以及随机产量三部分组成，趋势产量表示社会生产力的水平对粮食产量的影响，气候产量体现了气候因子对粮食产量的影响。在研究干旱与粮食产量之间关系时，需要对原始的粮食产量数据进行消除趋势化的处理，以此能够反映出干旱对粮食产量的影响。常用的方法有滑动平均法和HP滤波法等。本文则利用5 a滑动平均法和HP滤波法来对吉林省粮食产量数据进行去趋势化处理，通过对吉林省历年的粮食产量数据，技术发展水平以及气候产量与历年灾害情况之间是否一致分析，发现5 a滑动平均法更具科学性，因此选择5 a滑动平均法，其具体计算方式可见参考文献[31]。

2 结果与分析

2.1 MSBP指数构建的有效性

在计算出吉林省44个县级地区从1988-2017的SPI、SBI和MSBP的时间序列之后，对所有县级地区的SPI、SBI和MSBP之间进行相关性分析，其结果如图2所示。

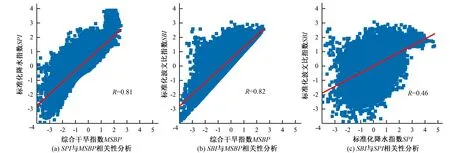
图2 不同干旱指数之间的相关性分析Fig.2 Correlation analysis between SBI, SPI and MSBP

从图2可以看出，SBI与SPI之间的相关性为0.46，这表明SBI在一定程度上能够反映出SPI的变化，是符合土壤湿度对降水的响应关系，意味着基于波文比来构建干旱监测指数是具有合理性和有效性。MSBP与其他两个指数之间的相关性为0.80以上，属于显著相关，这表明通过Copula函数方法联合波文比和降水来构建MSBP是具有一定的可靠性。

为了消除年内不同月份和不同地方所带来气候特点的差异，将吉林省44个县级地区从1978-2017的SPI、SBI和MSBP的时间序列按照不同月份和不同地区进行分组，然后分别进行相关性分析，其结果如图3所示。

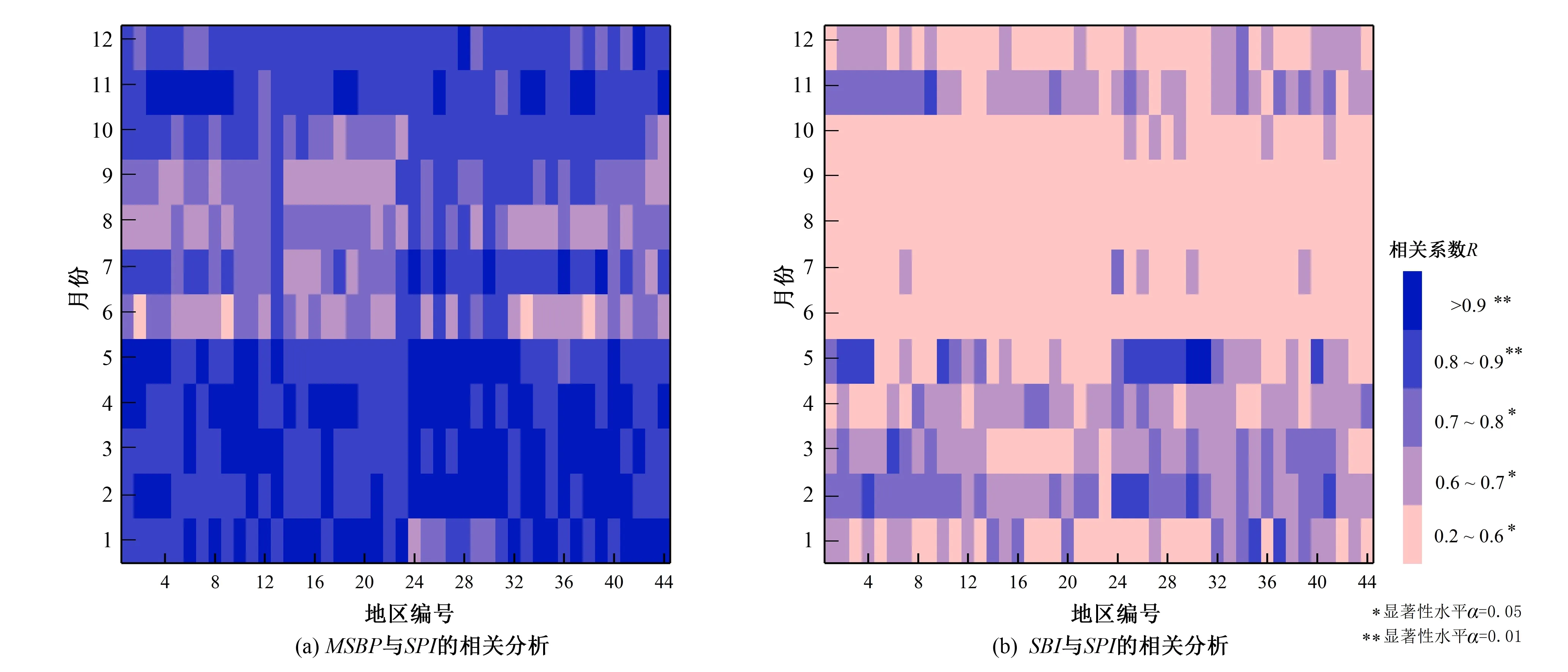
图3 基于波文比构建的指数与SPI的相关分析Fig.3 Correlation analysis of SPI and Index based on bowen ratio

由图3可知，MSBP和SBI与SPI之间的关系在不同县级地区的表现基本相似，但在不同月份呈现出很大差异。在1-5月和11-12月期间，SBI与SPI之间的相关性在0.6左右，MSBP与SPI之间的相关性在0.8左右，但在6到10月份期间，SBI与SPI之间的相关性在0.5以下，MSBP与SPI之间的相关性在0.6左右，低于年内其他月份的相关关系。通过结合图1和图2可以看出，SBI和SPI之间的关系在不同月份上会有明显的差异变化，在降水较少的月份(1-5月和11-12月)，SBI与SPI之间的关系比较显著；在降水较多的月份(6-10月)，SBI与SPI之间的关系开始变弱，相比于SBI，MSBP与SPI之间的关系在任何月份都要更加显著，在一定程度上弥补SBI在降水较多的月份(6-10月份)上的局限性，在干旱监测上的应用更具备优势。

2.2 MSBP的时间分布特征

2.2.1MSBP在年际的分布特征

为计算出吉林省整体的干旱指数，需要将吉林省各个地区的干旱指数值进行加权平均，不同地区的加权系数表明该地区对影响整体干旱状况的重要程度，由于本文研究涉及干旱指数与粮食产量之间的关系，故采用各地区的粮食产量对总产量的占比来作为加权系数。根据吉林省统计年鉴的记录，可以得到吉林省每个县级地区从1988年到2017年的粮食产量，由此可以通过地区多年平均产量和吉林省多年平均总产量的比值来计算出每个地区的产量加权系数。将吉林省各个县级地区SPI、SBI和MSBP的时间序列乘上各自的产量加权系数再求和就可以得到整个吉林省在1988-2017年间干旱变化的时间序列，其结果如图4所示。

图4 吉林省不同强度干旱事件发生时间分布图Fig.4 The temporal distribution of droughts with different intensities

从图4可以看出，在吉林省1988-2017年间，MSBP所显示的干旱事件分布要比SPI和SBI密集，SPI和SBI所显示的干旱事件分布的密集程度较为相似，但3个指数在显示吉林省1988-2017年干旱变化上的表现并非一致。MSBP在2004年以后轻旱事件分布的密集程度明显降低，中旱事件分布的密集程度略微降低，但在重旱和特旱事件上的分布更加密集；SPI在1988-2017年整个历史周期内各个干旱等级的干旱事件分布较为均匀，因此并无明显的干旱变化趋势。SBI在2009年以后轻旱和中旱事件分布的密集程度都明显降低，表现出干旱变化趋势是逐渐减轻的。

通过上述分析可看出SPI和SBI所显示吉林省1988-2017年的干旱变化上是不同的，这种差异是由于SPI和SBI是从降水和土壤水分两个不同方面来表征干旱特征所造成的，这也说明了仅靠一个指数来反映吉林省整体的干旱时间变化具有很大的不确定性，而MSBP能够结合SPI和SBI两方面来表达干旱特征，使得在识别干旱事件上更加精准，从而能更加准确地反映出吉林省1988-2017年的干旱时间变化。

2.2.2MSBP在年内的分布特征

根据吉林省在1988-2017年间的干旱时间分布情况，统计3个指数的不同程度干旱在年内每个月份的发生次数，并以此画出风向玫瑰图，其中竖轴线上的数字表示不同程度干旱的发生次数，圆圈外的数字表示月份(图5)。由图5可知，3个指数在风向玫瑰图的分布形状并非一致，表明不同指数所显示的干旱在年内分布情况有所不同。从发生干旱的次数分布来看，SPI和SBI在不同月份上的分布较为一致，干旱集中发生在2-3月份和8-9月份，而MSBP每个月所统计发生干旱的次数基本一致，并且年内干旱分布均匀，没有明显的月份差异。从干旱程度来看，3个指数在不同程度干旱的分布月份上也有所不同。对于轻度干旱，MSBP主要发生在3-6月和8月，SPI和SBI所显示的干旱分布基本一致，主要发生在2-3月、5月和8-9月；对于中度干旱，MSBP主要发生在6-11月，SPI主要发生在4-6月和9-10月，SBI主要发生在4月，7月和10-11月；对于重度干旱，MSBP主要发生在6-11月，SPI主要发生在6-8月,SBI主要发生在9-11月；从特重干旱，MSBP主要发生在6-9月，SPI主要发生在6月，7月和9月，SBI主要发生在8月。

图5 不同强度干旱发生频次的年内分布图Fig.5 The temporal distribution of drought frequency with different intensity

通过比较SPI、SBI和MSBP在不同程度干旱在年内不同月份的分布情况，可以看出SPI和SBI在不同程度干旱下干旱主要发生的月份是基本一样，而MSBP在不同程度干旱发生的月份要比其他两个指数多，在不同程度干旱下对每个月份所统计的干旱次数也比其他两个指数多，因此，MSBP对干旱的捕捉较灵敏。

2.3 MSBP的应用效果分析

2.3.1MSBP在干旱严重年份上的监测效果

根据中国统计年鉴中受灾面积和农作物耕种面积记录来计算出受灾率，并选取受灾率在40%以上的年份，其分别为1989,1997,1999,2000,2001,2004和2007。针对这些年份绘制出不同指数的时间序列，其结果如图6所示。

从图6可以看出，在历史干旱严重年份上，3个干旱指数在年内的波动趋势是具有一定的相似性，但是在个别月份却有着明显的差异，其主要集中在5-10月份。根据5-10月份的表现，可以看出当3个指数都显示出干旱时，MSBP显示的干旱程度要严重。MSBP本质上是通过Copula方法计算出SPI和波文比的联合概率，在SPI和波文比都显示干旱的时候，SPI和波文比的联合概率会更小，因此MSBP会显示出比单一指数更为严重的干旱，这表明在仅靠着单一指数识别干旱的条件下，很可能出现无法捕捉干旱的情况，而MSBP结合了土壤湿度和降雨两方面因素来弥补这一缺陷。

图6 在干旱严重年份下SPI指数、SBI指数、MSBP指数对比Fig.6 Comparison of SPI, SBI and MSBP in severe drought years

为进一步评估不同指数干旱监测的具体表现，根据中国气象年鉴里的记录确定出吉林省在干旱严重年份上干旱发生的时间范围，然后采取干旱强度(S)、干旱烈度(F)和干旱历时(D)来比较不同指数在历时干旱严重年份下的具体表现，其结果如表3所示。

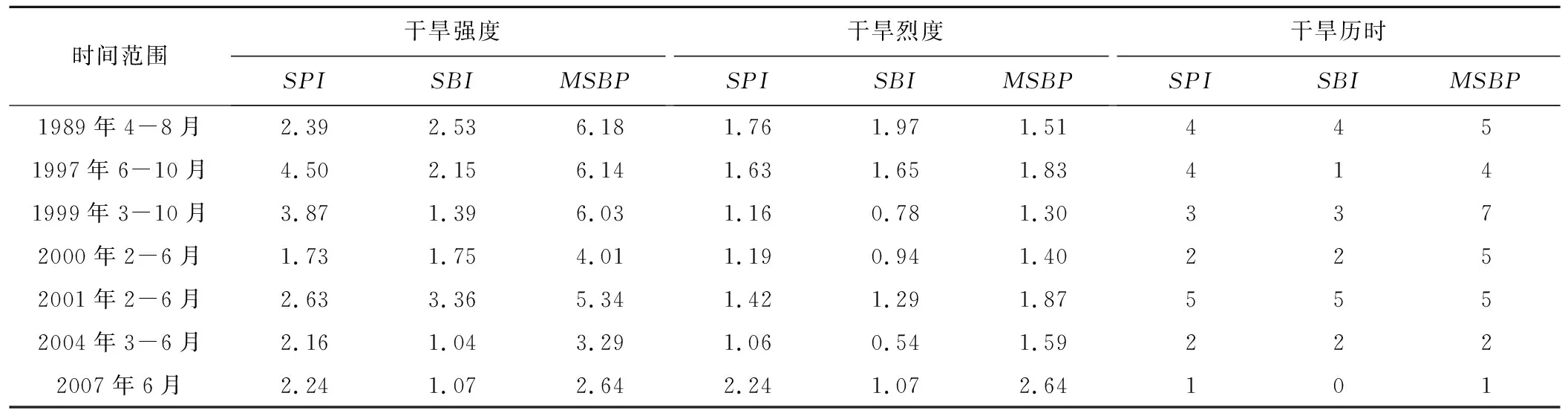
表3 干旱严重年份下不同指数的干旱特征Tab.3 Classification of SPI drought grade

由表3可知，在干旱强度上，MSBP远远大于SBI和SPI，表明在刻画干旱发生整个过程中逐月干旱所累积的干旱效应要好于SBI和SPI；在干旱烈度上，MSBP、SBI和SPI基本相差不大，只是MSBP要比其他两个指数略微高些，这说明3个指数都能够比较好地捕捉到单月份所发生的干旱；在干旱历时上，MSBP要长于SBI和SPI，而SBI和SPI基本上是处于一致。总的来说，在干旱发生的整个过程中，相比于SBI和SPI，MSBP能够灵敏地捕捉到干旱的开始与结束和干旱烈度，和实际发生的干旱状况较为一致。

2.3.2MSBP在粮食产量上的监测效果

根据吉林省在1988-2017年不同月份的MSBP、SBI和SPI指数值和该年吉林省粮食气候产量两组数据来进行相关性分析，可以得出吉林省在不同月份的MSBP、SBI和SPI与该年粮食气候产量之间的相关性，以此来探究MSBP、SBI和SPI在刻画干旱对粮食气候产量影响上的表现，具体结果如图7所示。

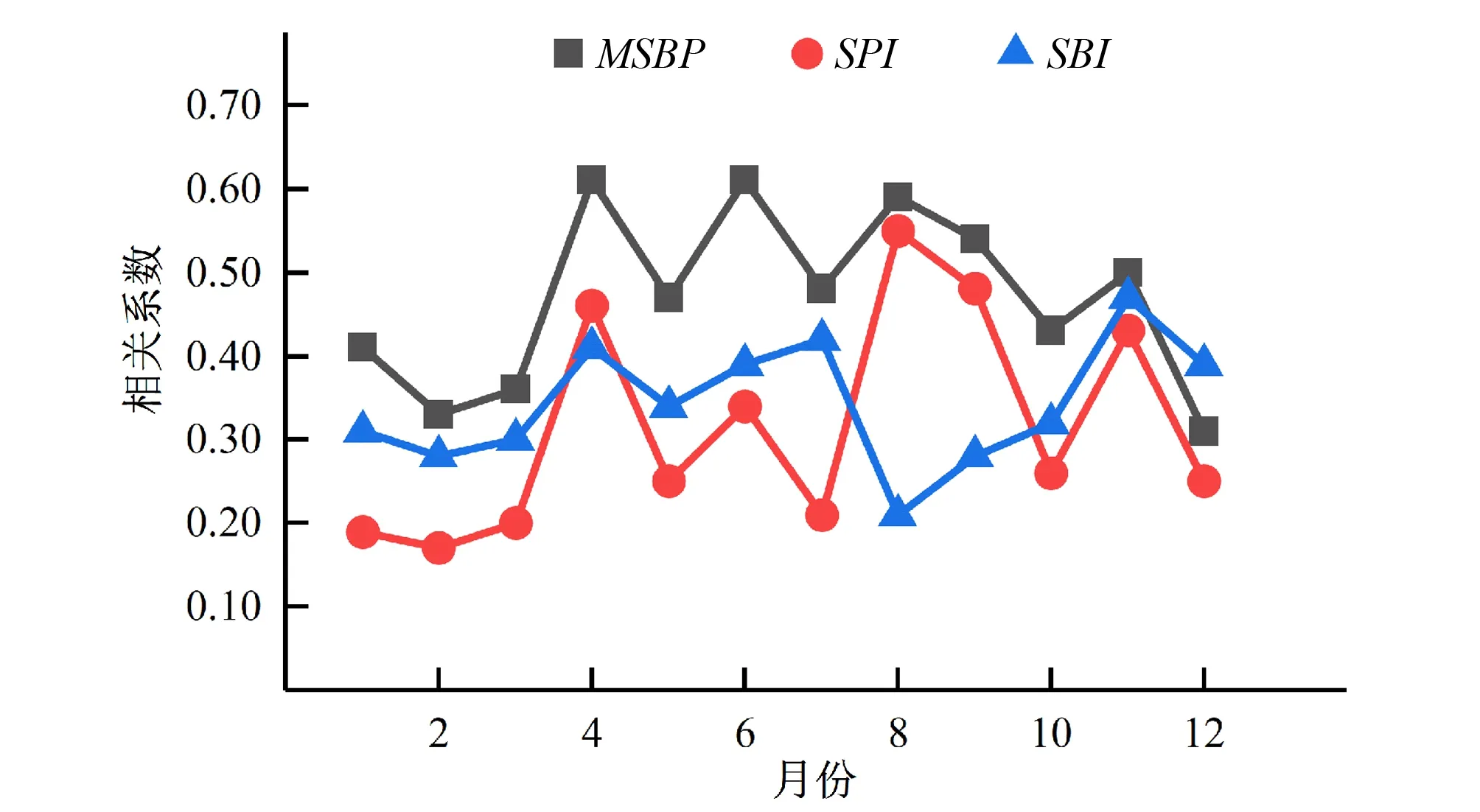
图7 干旱指数与粮食气候产量的关系Fig.7 Relationship between different drought indices and grain yield

由图7可知，MSBP、SBI和SPI与粮食气候产量之间的关系基本呈正相关关系，符合干旱对粮食产量影响的特点，MSBP与粮食气候产量之间的关系在不同月份上的波动比较稳定，而SBI和SPI与粮食气候产量之间的关系在不同月份上的波动较大。在1-3月份，MSBP、SBI和SPI所显示的干旱对粮食产量的影响均为较弱；在4-7月份，MSBP、SBI和SPI与粮食气候产量之间的关系普遍要好于1-3月份，但在5-7月份上，SBI与粮食气候产量之间的相关性要比SPI好；在8-9月份，MSBP和SPI与粮食气候产量之间的相关性较高，而SBI与粮食气候产量之间的相关性较差。在10-12月份，吉林省的农作物主要处于越冬阶段，对土壤分和降水并非和生长季一样敏感，因此MSBP、SBI和SPI与粮食气候产量之间的相关性开始降低。根据吉林省统计年鉴以及研究表明，吉林省主要的粮食作物为玉米和水稻，其主要生长季在5-9月份，相比于SBI和SPI，该时期内的MSBP与粮食气候产量之间的关最为明显，其相关系数均在0.45以上，可以较好地反映出干旱对粮食气候产量的影响。

由上述分析可知，MSBP、SBI和SPI与粮食气候产量之间的关系在4-9月份上最为明显，故根据1988-2017年吉林省不同干旱指数和粮食气候产量数据，绘制出MSBP、SBI和SPI在4-9月份的数值及粮食气候产量距平随时间变化序列，以此评估干旱对粮食产量的波动变化，其结果如图8所示。

由图8可知，在1988-2017年整个历史周期，粮食气候产量是呈现增长的趋势，MSBP、SBI和SPI所显示的干旱程度与吉林粮食产量整体上呈现负相关关系，基本符合述干旱变化与粮食产量波动变化之间的相互作用特点。在1988-2004年间，粮食产量距平在此段时间内主要处于低于平均水平的状态，在此期间的MSBP所显示出的干旱频率和干旱程度要比SBI和SPI高一些，SBI和SPI显示出的干旱频率基本一致，但SPI所显示出的干旱程度要比SBI高。当粮食气候产量处于历史最低点时(1989，1997和2000年)，相比于SBI和SPI，MSBP在这3个年份中表现出更为严重的干旱程度和更为长久的持续时间，表明当发生严重干旱时，MSBP在描述干旱对粮食气候产量造成波动变化上会更准确。在2004年以后，粮食气候产量距平主要处于正值的状态，并开始呈现明显的增长趋势，MSBP、SBI和SPI所显示的干旱频率都大幅度降低，但在个别月份上会出现干旱程度极其严重的情况，尤其是在2014-2017年份上，相比于SBI和SPI，MSBP在个别月份上会显示出更加严重的干旱，而当年的粮食产量并没有受到太大的影响，这可能是因为干旱发生的时间并非在作物生长的关键期，且干旱持续时间较短，并未对作物整个生长过程起到实质性影响，因而出现单月份严重干旱但整体产量未受到很大影响的现象。

图8 干旱指数与粮食产量距平的变化曲线Fig.8 Curves of variation between different drought indices and grain yield anomalies

总的来说，通过分析和比较MSBP、SBI和SPI与粮食产量波动变化之间的关系以及对粮食气候产量的作用可以看出，MSBP在表示干旱与粮食气候产量之间的相互作用比其他两个指数要更准确，比单一指数考虑得更加全面，综合性更强，在粮食产量上的监测效果要比SBI和SPI好。

3 讨 论

本文首次将反映地气能量变换的物理量波文比引入到遥感干旱监测领域上，并通过Copula方法结合波文比和SPI来构建出综合干旱监测指数MSBP。相比于土壤湿度的遥感产品来说，MSBP是通过地表能量平衡原理和地表干湿程度来刻画在土壤湿度方面的干旱特征，使得MSBP的准确性不会受到地表覆盖差异的影响，可以避免土壤湿度遥感产品因不同地区的地表覆盖差异所带来的不确定性的问题。因此，MSBP对遥感干旱监测指数的创新具有开拓意义。

除了利用植被指数进行干旱指数构建之外，也可利用蒸散发数据来构建干旱指数，这种构建方法是从土壤和植被蒸散发方面来表达干旱特征，此类的干旱指数虽能反映出历史上严重干旱事件，但在描述干旱所发生的程度上仍有偏差，如赵焕基于干旱稀遇程度和MODIS的蒸散发数据来构建农业干旱指数IEDI，尽管IEDI月值在年际间的极大值能够捕捉到历史严重的干旱事件，但此时的IEDI值所对应的干旱等级基本处于中度农业干旱程度，且所显示的干旱与历史严重干旱发生的月份并非完全一致，无法较为准确地反映出历史干旱严重的具体程度和发生时间[32]。这可能是因为在构建IEDI时未考虑降水的因素，使得当降水成为形成干旱的主导因素时，会弱化IEDI对干旱程度的判断。相比于农业干旱指数IEDI,MSBP不仅通过结合波文比指数来表达出土壤的蒸散发特性，而且还能够考虑到降水的因素，因此MSBP会在干旱事件特征上把握的要更加准确一些。

对于干旱指数的监测效果，许多研究通过干旱指数对农作物产量的影响来评价。余慧倩[33]利用MODIS遥感产品构建了基于NDVI和ET/PET的干旱指数DSI来分析干旱对农作物产量产生的影响，其DSI值与冬小麦产量之间的相关系数主要集中在-0.4到0.4之间；赵焕基于MODIS的蒸散发数据和干旱稀遇程度构建农业干旱指数IEDI来分析东北三省的干旱对粮食产量的影响，其相关系数均大于0.6；吴欣睿[34]通过MDOIS遥感产品将归一化植被指数(NDVI)和地表温度(LST)计算成温度植被指数(TVDI)，以此研究TVDI和粮食产量之间的关系，其相关系数最高达0.9；尽管上述研究构建的各种干旱指数能够较好地反映干旱对粮食产量的影响，但存在数据集可用的时间序列较短的问题，使得在反映干旱的精度上仍有较大的不确定性，而本文利用波文比和SPI构建的MSBP与粮食产量之间的相关性虽不是最显著，但所用的GLDAS数据可以获取到从1948年到至今的数据，其较长的时间序列在一定程度上解决数据量不足的问题，也能够为研究长时间尺度下的干旱提供一个办法。

尽管MSBP的干旱监测效果不会受到因地表覆盖差异所带来的影响，但通过分析MSBP和SPI之间的关系在不同月份和站点的表现可以看出，在6到10月份期间，MSBP与SPI之间的相关性要低于年内其他月份 (图2)。马英赛研究表明，当土壤湿度超过一定程度的时候，波文比由于数值过小，由此对土壤湿度的敏感性变得十分微弱，并不能够较为准确地描述出对应的土壤湿度水平，仅仅能够表示出此时土壤处于水分充足的状态[35]。6到10月份是一年内降水水平较为高的月份，当土壤湿度会变得较为湿润时，同时期波文比之间的差异集中在0～0.8范围内甚至更小，基于频率分布和累积概率计算出的MSBP是会放大这种差距，使得可能会出现严重低估土壤湿度问题，因此MSBP并不适用在土壤常年处于较为湿润状态的地区来进行遥感干旱区域监测，会出现高估干旱程度的现象，使得与真实情况不符。

4 结 论

(1)MSBP在描述干旱特征上比SBI和SPI更加全面和准确，在历史干旱严重的年份方面上，MSBP较为准确地刻画出在一年中发生干旱过程的持续时间以及不同时间下的干旱强度，其干旱监测结果与实际发生的干旱较为一致，是一个能够很好地应用在干旱监测领域上的综合干旱指数，可为区域遥感干旱指数的构建提供一个参考。

(2)MSBP能够较好地反映出干旱变化对粮食产量造成的波动变化。与此同时，MSBP充分利用SBI在刻画干旱对粮食产量的影响上的优势的同时，还能够结合干旱在降水方面的特征，使得MSBP与粮食产量之间的相关系数达到0.3～0.7。

(3)当土壤处于非常湿润状态时，SBI在表征土壤湿度水平上是具有一定的局限性，可能会出现严重低估土壤湿度问题，导致SBI所显示出的干旱程度与真实情况不符，尽管MSBP通过结合SPI来弥补这缺陷，但仍无法完全解决这一问题，因此MSBP并不适合在土壤非常湿润条件下反映当时的土壤水分状况。