基于改进Smith预估补偿的智能滴灌系统模糊PID控制

王 正，孙兆军

(1.宁夏大学新华学院，银川 750021；2.宁夏大学土木与水利工程学院，银川 750021；3.宁夏大学环境工程研究院，银川 750021；4.教育部中阿旱区特色资源与环境治理国际合作联合实验室，银川 750021)

0 引 言

智慧农业[1]的发展主要取决于基础设备的研发和创新，而智能灌溉系统是最重要的基础设备之一[2]。智能灌溉通过感知作物的生产环境，如土壤湿度、雨量和气温等，制定出合理的灌溉制度，实现了作物精准灌溉和自动化管理[3-5]。

由于智能滴灌系统具有结构简单、易操作、适用性广等优点，受到了广泛关注[6,7]。然而，滴灌系统是一种典型的惯性时滞、强耦合、易受干扰的非线性系统[8]，很容易发生不稳定。研究表明，在控制系统中加入Smith预估补偿器能很好地消除上述不利影响，且Smith预估控制被认为是解决大时滞过程控制的最有效方法[9]。张磊等[10]为解决由于被控对象参数的不确定性引起的系统失稳问题，提出基于Smith预估器的PD模糊控制策略，系统鲁棒性明显提高，仿真效果较好；刘斌等[11]提出将Smith预估模糊控制应用于温室灌溉决策中，系统误差不超过7.5%，有较高的实用性和稳定性；郝竹银等[12]介绍了加入Smith预估器的模糊PID算法控制温室温度的方法，结果显示相对于普通PID和模糊PID，其精度和稳定性有很大的提高；曾庆良等[13]针对研究对象时滞性和易受干扰的问题，设计了Smith预估的模糊PID控制方法，实验测试说明该方法具有较强抗干扰能力和较短的调节时间等。

虽然，上述研究利用Smith预估器在某种程度上提高模糊PID控制的稳定性、精度和抗干扰能力，但该预估器非常依赖精确的数学模型，考虑系统模型参数易受环境、设备等不确定条件变化的影响，推求精确模型的困难较大。因此，本文对传统Smith预估补偿器进行结构优化，解决由于被控对象的模型不适配引起的控制决策失误问题，从而提高系统的鲁棒性。1 智能滴灌系统数学模型通过建立水泵电机、水泵供水系统和其他控制及检测元件等环节的数学模型，进一步构建智能滴灌控制系统的传递函数。智能滴灌系统是利用变频器来调节水泵供水量，而变频器调节水泵电机转速过程可近似为一个惯性环节[14]，数学表示为：

(1)

式中：K1表示放大系数；T1表示惯性环节时间常数，由变频器和水泵性能决定；s表示符号算子；Nm(s)表示水泵电机转速nm(t)的Laplace变换；F(s)表示变频器输入频率f(t)的Laplace变换。

智能滴灌系统采用变压供水模式，即供水压力不断增加，增加到某一值时维持稳定，由压力上升阶段和恒压阶段组成[15]。变压供水过程可用时间常数为T2的惯性环节和时间常数为τ的延时环节串联近似描述，其中，T2由滴头数量决定，τ由管网长度及水流速度决定，数学表示为：

(2)

式中：K2表示放大系数；s表示符号算子；Np(s)表示水泵转速np(t)的Laplace变换；P0(s)表示水泵输出供水压力p0(t)的Laplace变换。

通常，可理想化地将滴灌系统其他控制及检测元件的数学模型假定为比例环节[14]，数学表示为：

G3(s)=K3

(3)

为简单起见，认为系统中电机转速nm(t)与水泵转速np(t)相等，即nm(t)=np(t)，故整个滴灌系统闭环传递函数可表示为：

(4)

滴灌系统结构方框图如图1所示。

图1 设施智能滴灌系统结构方框图

1 改进Smith预估补偿器设计

由以上分析可知，可利用Smith预估补偿器算法来解决滴灌系统存在延时滞后的问题。基本思想是：通过加入预估补偿环节消除系统模型中的延时环节，使被延时的信息及时送入系统执行部分，从而减少系统超调量和响应时间。但只有建立精确的系统数学模型基础上，基本型Smith预估补偿器才能发挥较好的作用，然而滴灌系统数学模型参数很容易受环境变化的影响，因此，需要对其进行改进。本文在基本型预估补偿器的基础上增加了系统控制和执行部分数学模型的补偿环节，减小了由于模型失配引起的不利影响，改进后的Smith预估补偿器如图2所示。

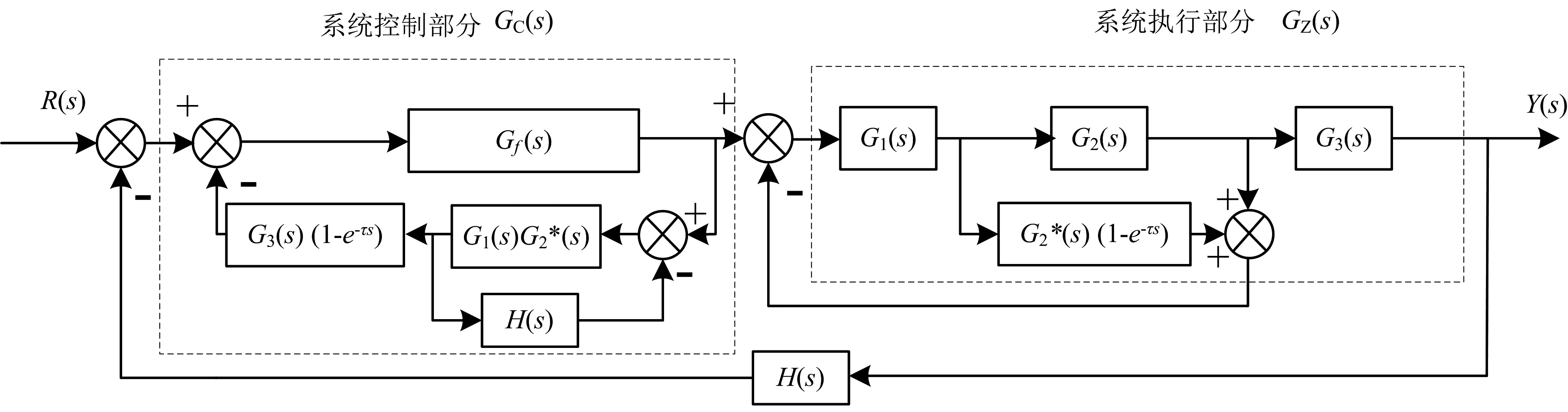
图2 改进Smith预估补偿器

图2中，Gf(s)表示模糊PID控制器的等效传递函数，G1(s)、G2(s)和G3(s)分别由式(1)、(2)和(3)给出，G2*(s)为系统变压供水过程除去延时环节的模型，即G2(s)=G2*(s)·e-τ s，H(s)为反馈回路传递函数，H(s)=1。

由图2可知，系统执行部分加入预估补偿器后的数学模型为：

(5)

系统控制部分加入预估补偿器后的数学模型为：

(6)

则系统的闭环传递函数为：

(7)

由式(7)可以看出，通过对系统执行部分和控制部分分别进行Smtih预估补偿后，系统传递函数的特征方程为：

(8)

式(8)中不含延时环节，因此加入改进Smith预估补偿器不会对系统稳定性产生消极影响，且系统参数变化对系统模型的影响也较小。

2 模糊PID控制器设计

通过向专家咨询及总结操作者经验，制定如表1所示的模糊控制规则。

以上控制规则根据专家及操作者的经验、知识给出，而模糊推理算法采用Mamdami“最小—最大”推理法，解模糊过程采用加权平均法。

表1 模糊PID控制规则

3 仿真测试与结果分析

通过对已采集数据进行系统模型参数反演，计算得到系统的参数分别为：T1=0.967 9，T2=0.242 1，K1=1.012 9，K2=0.930 6，K3=0.552 1，τ=0.914 7。系统传递函数为：

(9)

为了验证改进Smith预估补偿的智能滴灌系统模糊PID控制的有效性，在MATLAB R2014a/simulink平台进行建模与仿真，其结构如图3所示。

图3 智能滴灌系统的Simulink模型

通过不断调试，模糊PID控制器的3个参数初始值分别设置为Kp0=0.850 0，Ki0=0.450 0，Kd0=0.360 0时，控制效果较好。考虑到最佳土壤湿度为50%左右，因此，在本研究仿真测试中假定土壤湿度初值为0，将大小为0.48的阶跃信号作为智能滴灌系统的输入，分别进行PID、模糊PID(Fuzzy PID)和改进Smith预估补偿的模糊PID(Smith Fuzzy PID)等3种控制方法的仿真实验，仿真时间设置为30 s，采样周期为0.1 s，结果如图4所示。

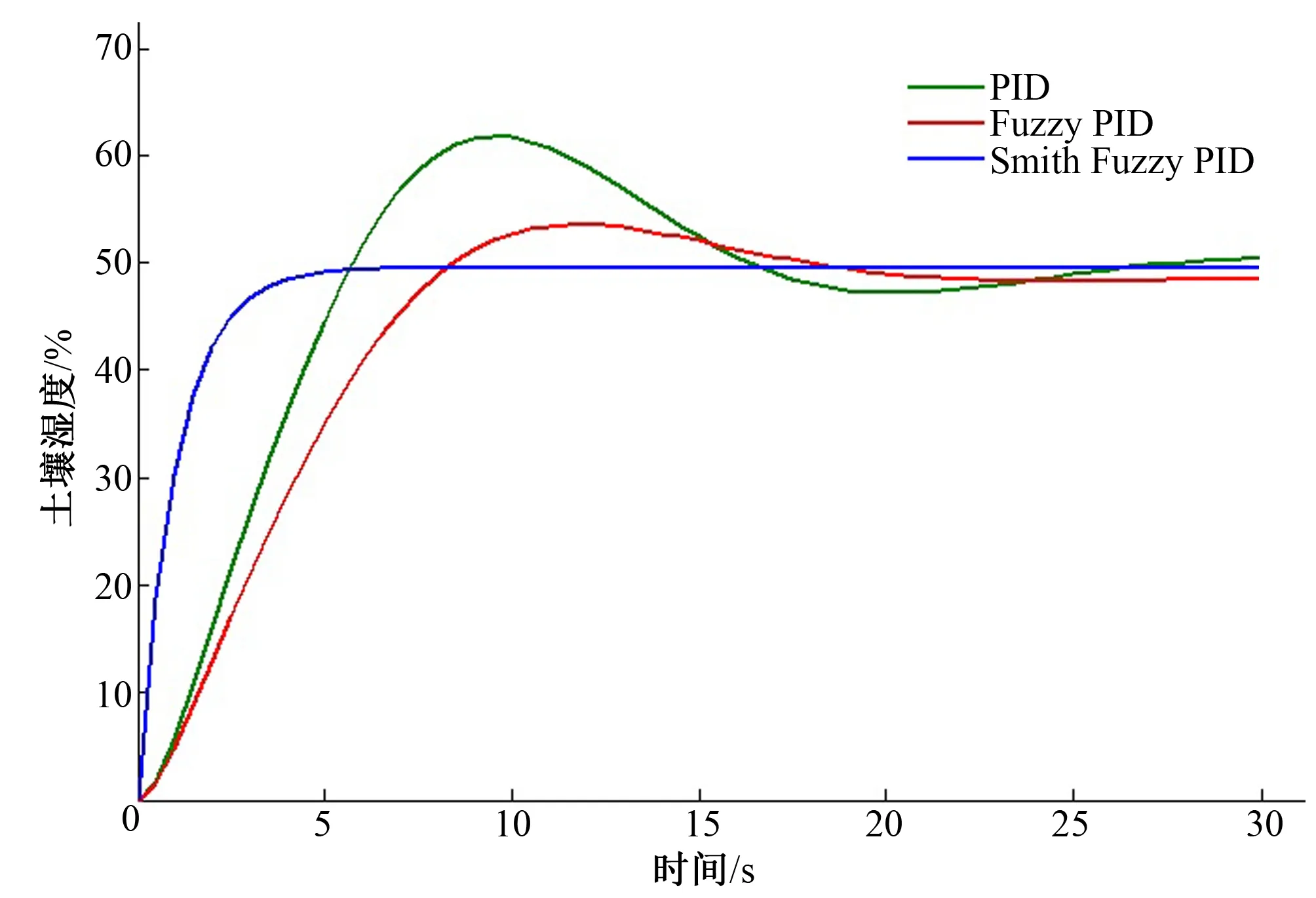
图4 土壤湿度仿真曲线

根据图4可知，针对时滞、惯性、非线性的智能滴灌系统来讲，3种控制方式中改进Smith预估补偿的模糊PID控制系统响应最好。由于PID控制和模糊PID控制没有加入预估补偿环节，系统超调量较大，且调整时间过长，虽模糊PID相对于PID的控制性能有所提高，但上升时间过长。而加入改进Smith预估补偿的模糊PID控制的土壤湿度响应曲线较平滑，无超调量，稳定性较强，调整时间和上升时间较短，稳态误差较小，表明本文所提出的控制方法改善了系统控制品质，系统能很快地进入稳定工作状态，增强了系统的稳定性和鲁棒性，它们的各项性能指标对比如表2所示。

表2 控制系统各项性能指标对比

4 系统测试

于2019年7月21日在宁夏大学科技园的蔬菜温室中，针对智能滴灌系统的功能、性能、稳定性等进行测试，系统安装低功耗无线传输网络，用于采集湿度传感器的数据。每隔5 min对土壤湿度进行采集，并通过无线网络返回系统控制部分，控制部分利用事先设定的控制策略对水泵电机转速和电磁阀实施作用，从而实现智能灌溉。改进Smith预估补偿的模糊PID控制土壤湿度曲线，如图5所示。

图5 改进Smith预估补偿模糊PID控制土壤湿度

实验中，设置蔬菜温室中土壤湿度值为60%，由图5可知，土壤湿度初值为19.86%，且灌溉5～10 min内土壤湿度迅速升高，在灌溉30 min时第一次到达设定值，灌溉45 min时达到最大值63.57%，最大超调量为5.95%，且土壤水分到达设定值后，土壤湿度一直稳定在60.22%左右，满足灌溉要求。

5 结 语

本文论述了加入改进Smith预估补偿环节的智能滴灌系统的模糊PID控制方法，通过预估补偿器消除系统模型参数变化对控制精度的不利影响。应用MATLAB/simulink工具箱对系统进行建模仿真，结果表明改进Smith预估补偿的模糊PID比传统模糊PID具有更好的控制品质和更快的响应速度；同时，在蔬菜温室中进行了田间实验，结果表明系统最大超调量为5.95%，且达到稳定后，土壤湿度保持在60.22%左右，符合灌溉要求。