基于二维三组元声子晶体带隙特性的振动研究

彭中波，李 成，高 阳

(重庆交通大学 航运与船舶工程学院, 重庆 400074)

0 引 言

声子晶体[1]是具有弹性波带隙特殊特性的周期性结构材料，是将多种材料或是微腔结构按照一定周期进行排列组成[2-4]。当弹性波在结构中传播时，处在带隙频率范围的弹性波会被衰减掉而无法继续传播[5]。声子晶体的带隙特性和组成该结构的材料参数相关，也和对应的结构参数有关，包括散射体的密度、弹性模量、散射体的形状尺寸、填充率、晶格形式[6-8]等。声子晶体独特的带隙特性，使其在实际的噪声隔离和振动控制等方面都具有潜在的应用前景[9]。

由于声子晶体所具有的特殊带隙特性，近年来吸引了大量学者对其进行研究。徐丽[10]利用平面波展开法，对二维二组元声子晶体散射体的排列方式，及不同散射体材料下的带隙特性进行了计算；张明[11]利用时域有限差分法，对二维二组元声子晶体在不同基体及散射体下的带隙进行了计算；张昭等[12]对不同散射体形状及填充率情况下的薄板型声子晶体的带隙及减振特性进行了计算；赵元年等[13]设计了一种二维Suzuki晶格声子晶体薄板，考虑到散色体填充率及板厚对带隙的影响，结合有限元法对该薄板结构的带隙及传输特性进行了计算；姜超君[14]等在散射体单一参数的基础上，利用有限元法对多参数情况下的二维二组元声子晶体的带隙进行计算。

现有研究对于声子晶体带隙影响因素及有限周期结构振动减振特性，大都集中在二维二组元方面。笔者设计了一种二维三组元固态声子晶体结构，结合有限元软件COMSOL对所设计结构的带隙进行计算，同时对有限周期结构下的传输特性进行计算，验证了能带结构计算方法的正确性和有效性。进一步讨论了该结构散射体填充率、包覆层厚度对第一带隙的影响因素。并在此基础上利用不同种材料的散射体再次对其传输特性进行计算，分析不同周期数下同种散射体，及同种周期数下不同散射体，对有限周期声子晶体结构振动特性的影响。

1 有限元模型及计算方法

笔者设计的二维三组元声子晶体单元结构如图1(a)，图1(b)为第一Brillouin区，图1(c)为该单元构成的4×4有限周期声子晶体结构。该单元结构是由散射体包裹上一层包覆层材料后，再嵌入到基体材料中构成。内部A为散射体，中间B为包覆层，外部C为基体。单元结构的晶格常数为a,散射体半径为r1,包覆层半径为r2。

目前对于声子晶体能带结构求解的方法有很多，常见如平面波展开法、时域有限差分法、集中质量法、有限元法[15-16]。笔者采用有限元法对设计的声子晶体进行能带结构计算。结合Bloch定理，将理想状态下具有周期性结构的声子晶体，用图1(a)设计的单元结构进行代替,并对其设置周期边界条件及引入Bloch波矢,再令波矢k对不可约Brillouin区的高对称边界(图1(b)中的阴影部分)进行扫描，从而求解出声子晶体的能带结构。

为对所计算的能带结构进行验证，更好观察对应带隙频率范围弹性波的衰减，建立有限周期声子晶体结构计算模型如图2,利用COMSOL有限元软件的固体力学模块，于结构的一侧施加边界载荷,对其进行传输特性计算,传递公式如式(1)：

(1)

式中：out(solid.acc)为振动加速度输出；in(solid.acc)为振动加速度输入。

2 仿真计算及分析

2.1 能带结构及传输特性计算

利用图1所述单元结构进行能带结构计算，其中a=20 mm,r1=5.5 mm,r2=8.8 mm，对应的材料参数见表1。

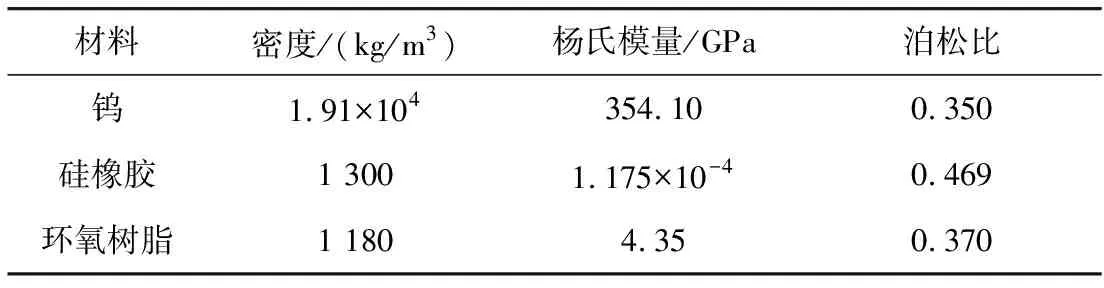
表1 材料参数

对图2中的有限周期声子晶体结构传输特性进行计算，能带结构及传输特性如图3。

由图3可知，在前8阶能带结构图中存在着2个完全带隙，对应的带隙范围分别为229.58～552.14 Hz及996.8～1 227 Hz。在这2个带隙对应的频率范围内，传输特性图中相对加速度的对数值均小于0，即在结构一侧所施加的振动激励在声子晶体结构中传播时，振动激励所产生的弹性波受到了衰减，且弹性波衰减的频率范围和能带结构的带隙范围基本吻合，这很好的验证了能带结构计算方法的可行性。同时也说明了声子晶体对于带隙频率范围内的弹性波，有很好的衰减抑制作用，达到减振的目的。

2.2 填充率及包覆层厚度对第一带隙的影响

保持该结构晶格常数a=20 mm，包覆层厚度d=3 mm，只改变散射体半径以研究该结构第一带隙的变化情况。散射体半径从4 mm增加到6.5 mm,对应的计算结果如图4。由图4可知，当散射体半径逐渐增大(即填充率增大)，第一带隙起始频率由278.03减小到222.44 Hz，截止频率由505.33增大到656.69 Hz。第一带隙截止频率增长速度明显大于起始频率下降速度，因此整体带宽呈现增长趋势，带宽由227.3增长到432.25 Hz。

保持晶格常数a=20 mm，散射体半径r1=5 mm不变，只改变包覆层厚度，研究该结构第一带隙变化情况。包覆层厚度从7增加到9.5 mm，对应的结果如图5。由图5可知，随着包覆层厚度增大，第一带隙的起始频率、截止频率均下降，起始频率由314.96减小到200.11 Hz，截止频率由715.22减小到421.2Hz。截止频率下降速度大于起始频率的下降速度，使得整体带宽呈现下降趋势，带宽由400.22减小到221.09 Hz。

2.3 不同周期数对振动特性的影响

为了更进一步探究该二维三组元结构在振动激励下的减振效果，同时为了避免单一散射体材料不具备说服性，也为了更好的说明不同周期结构对于振动特性的影响。保持振动激励力大小不变，依次对铅、钢、铝散射体构成的4×4、6×6有限周期声子晶体传输特性进行计算。硅橡胶、环氧树脂的材料参数如表1，保持结构尺寸不变，散射体铅、钢、铝的材料参数见表2。

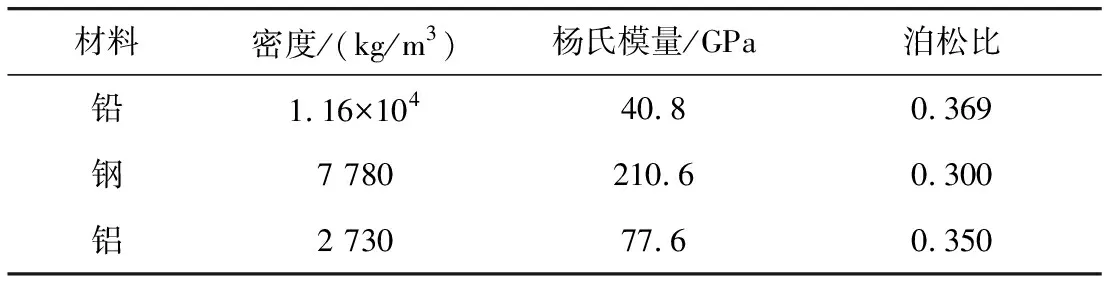
表2 散射体材料参数

对铅、钢、铝散射体对应下的能带结构分别进行计算，计算结果如图6。接着对铅、钢、铝散射体对应下的4×4、6×6有限周期结构的传输特性分别进行计算，计算结果如图7。

图6可知，3种散射体计算的能带结构在前8阶均有2个完全带隙。铅的带隙频率范围为292.65～576.58 Hz及967～1 227 Hz；钢的带隙频率范围为354.4～604.44 Hz及967.26～1 227 Hz；铝的带隙频率范围为571.57～721.21 Hz及 969.1～1 227 Hz。同时可以看出图7传输特性图中铅、钢、铝散射体对应的振动衰减频率范围与图6能带结构图中的带隙频率范围基本一致，进一步证实了能带结构计算方法的可行性。同样振动激励所产生的弹性波在这些带隙频段内均受到了衰减，即是起到了减振的作用。

由图7还可看出，同种散射体下的声子晶体在不同周期数下对于振动的衰减作用不同。在对应带隙频率范围内，3种散射体对应下的6周期结构对振动的衰减效果明显好于4周期结构，减振效果更好。但在非带隙对应频率范围内，同种散射体结构下的声子晶体，当增加周期数时，振动不但没有衰减，反而进一步被放大。图7(a)中频率范围为80～260 Hz、620～730 Hz、900～950 Hz及1 260～1 300 Hz；图7(b)中频率范围为70～210 Hz、590～730 Hz、900～950 Hz及1 260～1 300 Hz；图7(c)中频率范围为100～390 Hz、530～560 Hz、740～780 Hz、890～950 Hz及1 260～1 300 Hz，在这些非带隙对应的频率范围内，当增加声子晶体的周期数时会使得振动被进一步放大。

2.4 不同散射体材料对振动特性的影响

由2.3可知，当用铅、钢、铝3种不同散射体材料，分别计算各自对应有限周期结构的传输特性时，低频段振动衰减的频率范围均不同。因此，有必要探究在相同的周期数下使用不同散射体构成的声子晶体对于振动特性的影响。由于6周期结构声子晶体对振动的衰减效果比4周期好，笔者将钨、铅、钢、铝在6个相同周期数下的传输特性进行比较，传输特性如图8。

由图8可知，在230～710 Hz频率范围内，在6周期结构下，金属钨在230～520 Hz内实现 290 Hz频率范围振动的衰减；金属铅在300～550 Hz内实现250 Hz频率范围振动的衰减；金属钢在360～580 Hz内实现220 Hz 频率范围振动的衰减；金属铝在580～710 Hz内实现130 Hz频率范围振动的衰减。由此可知，随着散射体密度增大，对应的衰减频率会越低，且衰减的频率范围也会越宽，减振效果越好。

由于金属钨密度最大，由图8还可知，其相对加速度对数值也最小，对于振动的衰减效果也最好。想要对低频的振动进行有效的控制，起到很好的减振作用，在声子晶体有限周期下使用密度越大的散射体，对于振动的衰减效果也越好。

在频率范围970～1 240 Hz内，4种散射体材料对于振动衰减效果区别不大，因此在此频段内，想要实现振动的衰减，对于散射体金属密度的要求并不大，常见金属均能对此频段的振动进行有效的控制。

3 结 论

笔者设计了一种二维三组元声子晶体结构，结合有限元法，对其能带结构及有限周期声子晶体结构的传输特性，分别进行了计算。传输特性中出现的衰减频率范围和能带结构相对比基本吻合，验证了能带结构计算方法的正确和有效性。

当改变散射体填充率及包覆层厚度时，对应的第一带隙起始、截止频率均会改变，随之带隙的带宽也会改变。将铅、钢、铝3种散射体各自对应下的4×4及6×6有限周期数的传输特性进行计算，同时将同种周期数下的钨、铅、钢、铝4种散射体的传输特性进行比较，探究对于振动特性的影响。研究结果表明：在同种散射体不同周期下，当增加周期数时，对于带隙频率范围内振动的衰减效果也会增强，而在非带隙频率范围内振动反而可能会被放大。对于不同散射体同种周期下，在一定低频段内(230～710 Hz)散射体的密度越大，对于振动的衰减效果越好，衰减频率范围也越广；在相对频段内(970～1 240 Hz)，散射体的密度对于振动衰减效果区别并不大，常见金属均能对此频段的振动进行有效的控制。可以得出，该二维三组元声子晶体结构所实现的低频带隙范围对船舶的减振降噪具有潜在的应用前景。