一种永磁有限转角电机的磁场分析

2020-08-24姜保军周鹏飞

重庆交通大学学报(自然科学版) 2020年8期

姜保军，周鹏飞

(重庆交通大学机电与车辆工程学院，重庆 400074)

0 引言

有限转角电机是一种可在一定角度范围内直接驱动负载进行快速运动和精准定位的伺服电动机[1]。该电机具有结构简单、转动惯量小等特点，因此机电时间常数较小，且可承受较大的角加速度。该电机组成位置伺服系统具有出力大、频带宽、定位精度高、体积小、重量轻等特点，故可应用于航空伺服阀、舵机作动、机器人关节、雷达天线等高精度电气伺服系统中[2-3]。有限转角电机性能受其内部磁场影响，因此分析有限转角电机内部磁场具有重要实际意义。

目前针对有限转角电机结构设计优化主要集中于环形绕线式和转子永磁式这两种形式[4-6]。在电机磁场研究方面，传统旋转电机通常使用经典磁路分析法，场路结合法及有限元法[7-11]。但由于有限转角电机内部磁场不同于传统旋转电机，因此目前大多采用场路结合法和有限元法研究有限转角电机磁场。文献[1]针对双侧无槽永磁有限转角电机的电枢反应磁场，通过建立定子内侧与外侧所满足的泊松方程，分析了电枢磁场对主磁场的影响；文献[5]针对外转子与传统内转子的电机性能，通过建立绕线式有限转角电机磁场模型，得到了气隙磁密与电磁转矩解析式，并用有限元法进行了对比验证。目前尚未见到研究有限转角电机绕组电流与起动转矩关系的文献。

笔者主要针对某种阀体的开关要求，利用有限元分析软件Ansoft模拟了一种稀土永磁有限转角电动机的磁场，并分析电机定子绕组电流与起动转矩、转矩变化与转子位置角之间关系。

1 电机基本结构

该电机基本结构主要由嵌有永磁体的定子铁心、绕组和转子组成[12]。永磁体充磁方向为+X向(+X方向为N极)，绕组电流方向为右进左出，绕组产生的磁场沿+Y方向为N极，如图1。图1中：S1未转子极弧面与左半边定子重合的面；S2为转子极弧面与右半边定子重合的面。

2 理论分析

当定子绕组电流为零时，电机内部磁场仅由永磁体单独建立，此时转子应位于磁阻最小位置；此时转子凸极中轴线与Y轴(定子永磁体磁场交轴轴线)重合，转子只受到永磁体的力而保持平衡，如图2(a)。当电机位于初始位置且绕组通过电流时，定子永磁体磁场和定子线圈磁场共同作用形成电机内电磁场，定子永磁体附近铁心一部分出现增磁现象，而相对的另一侧将出现减磁现象，合成磁场分布发生畸变。图2(b)为绕组磁场，图2(c)为合成磁场畸变。此时转子凸极并不是位于磁阻最小位置，于是根据磁路遵循“最小磁路路径”原则，转子受到磁场力，转子将转动一定角度，达到磁阻最小的平衡位置，如图2(d)。

当转子转动一定角度且绕组通过电流变为零，电机内又仅存在永磁体磁场时，磁场分布发生改变，此时转子凸极又不位于磁阻最小位置，于是根据磁路遵循“最小磁路路径”原则，转子受磁场力的作用，转子将转动一定角度，回到磁阻最小的平衡位置。

3 仿真分析

3.1 仿真模型

利用Ansoft软件的Maxwell2D模块对此种有限转角电机的磁场进行了仿真分析，仿真模型基本参数如表1，仿真模型有限元剖分如图3。定子铁磁材料采用DW465-50，其B-H曲线如图4。图4中：0a段为起始磁化阶段，ab段为线性磁化阶段，dc段为临界饱和阶段，cd段为磁化饱和阶段。

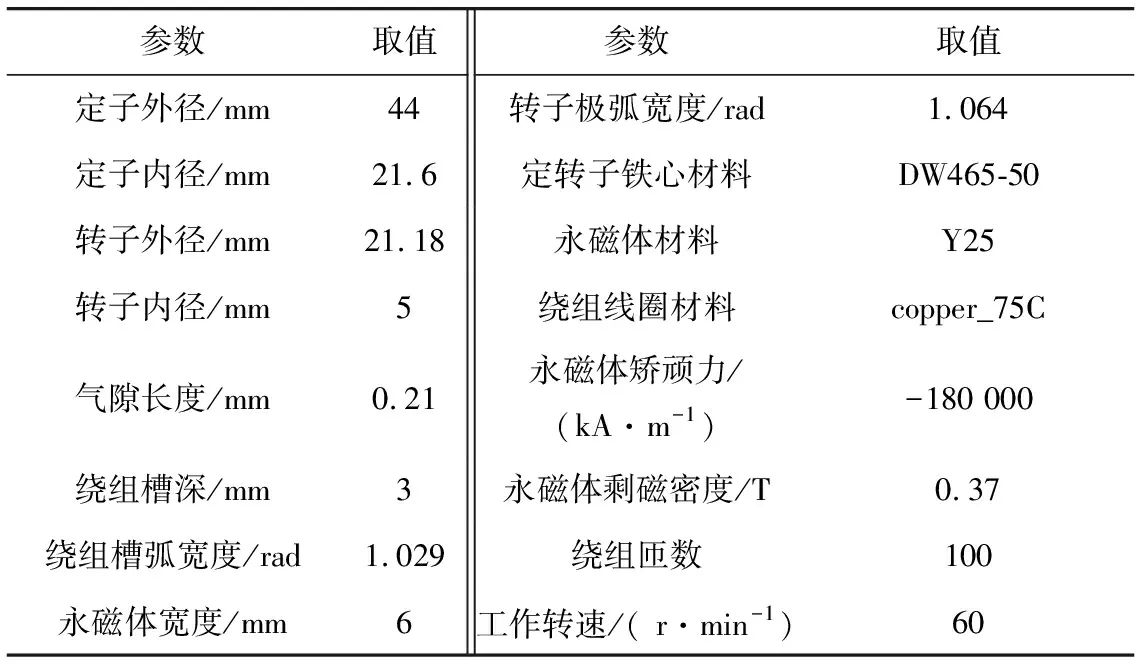
表1 仿真模型基本参数

图3为此电机有限元模型网格剖分。由于有限元网格剖分结果直接影响仿真分析精密程度，为此永磁体与绕组附近的网格剖分比较细密，定子内部的剖分则不密集；永磁体与定子接触的地方和绕组与定子接触的地方网格剖分也比较细密，最细密的是转子与永磁体和定子之间的气隙处。

3.2 仿真结果分析

图5为永磁体磁密分布。气隙磁密曲线是从电机转子左极尖到右极尖对应的磁密曲线，坐标原点0位置处为电机转子极弧左极尖处。由图5可见：永磁体气隙磁场分布关于Y轴对称，且该磁场交轴恰好与Y轴(磁密为零的物理中性线)重合。气隙磁密集中分在图1中的转子曲面S1、S2部分对应的空间上，但对称位置磁密大小相等方向相反。

图6为绕组励磁磁密分布。由图6可见：绕组励磁产生的磁密同样关于Y轴对称，同样也集中分布在图1所示的转子曲面S1、S2部分对应的上方空间，其对称位置的磁密大小相等方向相同。

图7为合成磁场气隙磁密分布。由图7可见：当气隙中永磁体磁场与绕组磁场同时存在时，气隙磁场为二者之和。由于转子曲面S1部分上方对应的绕组磁密作用为增磁，而曲面S2上方绕组磁密作用为减磁，于是合成磁场发生畸变，磁场轴线向面S1扭曲偏移。因此，根据磁阻效应，为了使磁路磁阻最小，电机形成转矩，转轴将发生偏移，形成一个角位移。

同理可得，当绕组定子绕组电流从某一确定值瞬时变为零时，电机气隙磁场也将变为仅由永磁体磁场建立，磁场畸变消失，磁场分布恢复为对称，转子曲面S1、S2部分上方磁场集中且对称分布。根据磁阻效应，为恢复为最小磁阻，转子将会受到一个使磁路磁阻最小的回正转矩，转子回到初始位置。永磁体单独工作时转子回正转矩如表2。

表2 永磁体单独工作时转子转矩

当定子绕组通入的电流值不同时，合成磁场轴线将发生不同程度扭曲偏移。当永磁体磁密不变时，在磁路线性区内，随着电枢绕组磁场磁密增加(即励磁电流增加)，由于转子凸极极面S1部分增磁效果显著，S2部分减磁效果显著，合成磁场轴线扭曲偏移程度也随之增大。于是转子角位移也随之增大。图8分别为定子绕组通入0.5、2 A时的合成磁场轴线扭曲偏移程度磁场场线图。同理，若改变定子绕组电流方向，则可改变转子转动方向。

图9为电机起动转矩与电流关系曲线。由图9可知：电机起动能力与定子绕组电流相关，起动转矩随着电流增大而增大，且两者之间成线性关系。

图10为在不同绕组电流值下，电机转矩随转子位置角变化曲线。由图10可知：电机转矩变化大致可分为：0°～11°、11°～28.5°、28.5°～32.4°和32.4°之后这4个阶段。这4个阶段分别对应材料DW465-50的4个磁化阶段，其中：0°～11°对应0a段；11°～28.5°对应ab段；28.5°～32.4°对应bc段；32.4°之后的曲线对应cd段。

图10中：在0°～11°电机转矩变化最大，且较大电流产生较大的转矩。图11为图10的局部放大。图11中：转子位于11°～28.5°位置角段时，随着转子位置角增加，转矩变化逐渐平稳，电流对转矩值得影响也逐渐变；在28.5°～32.4°位置角段时，因当电机铁磁材料达到临界饱和阶段，由于导磁能力下降，电机转矩再一次突变，电流对转矩的影响呈非线性关系，进而出现较大电流对应较小转矩这一现象。例如定子线圈通过4.5A最大电流时会产生最小转矩；定子线圈通过2A最小电流时会产生最大转矩。