公共交通管控对新冠肺炎病毒(COVID-19)疫情爆发期的影响分析

姬杨蓓蓓，莫世杰，成 枫

(上海大学 管理学院，上海 200444)

0 引 言

公共卫生突发事件不仅给民众健康带来威胁，更涉及到城市运转、社会稳定及社会经济的健康发展。例如：公元前5世纪，古希腊爆发的天花疫情导致雅典城一半人口死亡，严重影响了雅典社会经济发展；公元165—266年间爆发的Antonine瘟疫导致罗马帝国经济发展严重恶化。此外欧洲爆发的黑死病、西班牙爆发的流感、我国爆发的SARS病毒、西非爆发的埃博拉病毒等，无一不给人类生命健康和财产带来了巨大损失。在全球化进程日益加快的今天，随着海陆空3大交通运输网络的普及范围、速度和载客量持续扩大，流行病及其载体传播较以往任何时候都更迅猛[1]。

此次以武汉为中心的新冠肺炎病毒(COVID-19)疫情在全国爆发之际，以大容量、集约型为显著优点的公共交通很快便成为了病毒传播的高效途径。因此，在疫情爆发而国内外尚未研发出临床试验可靠的特效药和疫苗之际，湖北省确诊率已低于外省，极有可能出现医疗资源不足等情况[2]。全国各个城市根据自身情况在不同时刻对城市公共交通采取不同等级的管控措施。事实证明这些措施有效地降低了新冠肺炎的快速扩散，也使得我国的“战疫情”工作取得了阶段性进展，确诊病人和疑似病人数量在有效管控后显著下降。

与此同时，公共交通停运也给城市运行及民生带来了极大困难。此次疫情爆发后，我国各城市先后采取了不同的公共交通管控措施，并积累了丰富的经验。政府和相关管理者如何基于这些宝贵的经验，分析并制定合理、及时的应对重大疫情的交通管控机制，通过有效控制疫情传播的同时保证城市运行的基本平稳，是一个值得深入研究的课题。这对今后应对重大疫情爆发具有重要的参考意义和借鉴价值。

1 研究现状

针对公共卫生突发事件，相关学者从不同角度，采用不同方法进行了分析和研究。在数据分析及预测方面，中国疾病预防控制中心新型冠状病毒肺炎应急响应机制流行病学组通过对截止2020-02-11上报的所有病例进行流行病学分析得出：疫情将在2020-01-24至2020-01-26达到首个流行峰[3]；梅珊等[4]基于Agent仿真系统针对甲流的扩散开展仿真实验，实验结果表明：相较于第5 d启用管控措施，第4 d启用的感染人数降低一半以上，此外，约19%的人群会在公共交通子空间被感染；YANG Zifeng等[5]利用改进的SEIR模型计算出COVID-19流行曲线，并使用2003年SARS数据训练的LSTM模型对其进行预测，研究表明：及时地采取交通管控、居家隔离等措施对疫情防控有显著作用。在防疫策略方面，WANG Fusheng等[6]指出“我们应该坚持的基本策略仍然是疾病的早期发现、早期诊断、早期隔离和早期治疗”；薄涛[7]采用理论和实证相结合方法，以青岛为样本调查对象，构建了疾病预防控制机构(CDC)应急能力评价体系的STORM框架，探讨分析了突发公共卫生事件的应对机制；周继彪等[8]对此次新冠病毒爆发后的宁波公共交通现状进行分析，针对不同公共交通方式提出不同的组合防疫策略；许明星等[9]基于“心理台风眼效应”研究，从多方群体的风险感知差异角度提出4条有针对性的防范建议；刘远立等[10]在分析新冠肺炎疫情本身特点和全球新发传染病流行趋势的基础上提出在疫情防控进入“新常态”后，如何有效加强我国公共卫生治理体系和治理能力现代化的建议。在城市交通应急方面，针对新冠肺炎不同阶段的特点和传播规律，周文竹[11]提出不同城市的交通应急对策；李争光等[12]通过对正平衡点及无病平衡点的存在与其稳定性模型分析，发现人口快速流动会使交通较发达城市的染病者数量急速增加，进而加快疾病的传染速度，增加感染人数；刘晟[13]通过对传染病传播特点进行分析，提出不同交通方式下的线路规划解决方案。此外，诸大建[14]针对此次疫情防控中出现的现象，指出老百姓科学生活水平和城市治理现代化水平亟待提高；ZHAO Shi等[15]基于经典易感暴露传染病恢复模型开发出间隔流行病模型，通过博弈论的理论决策过程来模仿行为，从而实现对武汉COVID-19爆发的动态预测，通过改变关键模型参数，在几种公共干预措施下讨论了爆发的规模和时机。

综上所述，现有学者已对病毒传播机理、防疫策略、城市交通应急等方面展开了研究，强调公共交通管控在抑制疫情传播过程中发挥的巨大作用。但是当前城市公共交通管控强度和管控及时性对疫情传播影响仍缺乏定量分析，各城市公共交通管控策略缺乏科学指导。故笔者通过搜集疫情爆发初期全国56个城市公共交通管控策略、管控开始时间、经济水平和相对位置等相关数据，利用统计分析方法，从事件结果反推出各因素对疫情传播影响程度，为城市公共交通管理者提供科学数据支持。

2 数据收集

笔者重点分析了疫情爆发初期累计确诊病例影响因素。全国疫情于2020-02-18趋于平稳，呈显著下降趋势，2020-02-27全国(除湖北地区)新增确诊人数仅为9人，此后全国新增确诊人数逐步下降，各地陆续恢复公共交通，公共交通管控对累计确诊人数影响开始减弱或消散。笔者从国家和各省市卫健委官网收集了自2020-01-20至2020-02-28全国21个省级行政单位中56个城市每日疫情数据(累计确诊病例数、当日确诊病例数和疑似病例)，如表1。

表1 调查城市COVID-19确诊人数等级(截至2020-02-28)

由表1可知：湖北省外累计确诊人数超过400人的3个城市分别为北京、温州和重庆，均为经济发展水平高的城市，其中距离湖北最近的重庆累计确诊人数最多，达到576人；而另两个直辖市(上海和天津)的确诊人数虽然未到达400人，但也相对较高，分别为337、136人(数据截止至2020-02-28)；其次，由表1可见：累计确诊人数超过100人的城市基本分布在湖北省周边，距离越远，确诊人数越少。此外，笔者从各城市发布的官方通知中收集了56个城市的公共交通管控开始时间、管控强度；并从统计年鉴中收集各城市2019年的年生产总值(GDP)。

表2为疫情爆发初期，笔者所调查56个城市实施交通管控措施的分级情况。根据管控措施将其分为5类：公共交通无停运(Ⅰ级)、仅停运城乡线路(Ⅱ级)、城市支线停运(Ⅲ级)、分两阶段完全停运或一次仅保留少量线路(Ⅳ级)和完全停运(Ⅴ级)。

表2 疫情初期调查城市公共交通管控强度

针对减少班次的管控，笔者按照线路等级分为3类展开讨论：① 减少城乡线路班次，归为第2类仅停运城乡线路；② 减少城市支线班次，归为第3类城市支线停运；③ 减少城市主线班次，考虑到当城市主线班次开始减少时，城市支路和城乡线路一般采取完全停运或仅保留极少数重要线路的管控形式，因此笔者将其归为第4类分两阶段完全停运或一次仅保留少量线路。针对地铁、有轨电车等非常规公交方式，考虑到在疫情期间多数采取缩短运营时间和调整发车间隔的精细化管控措施，因此笔者根据其调整比例将其归为表2中的第5类。

由表2可知：采取完全停运(Ⅴ级)的城市主要集中在湖北、河南、江西、河北等相对距离较小、经济水平较低、公共交通停运代价较小的省份；采取公共交通无停运(Ⅰ级)或仅停运城乡线路(Ⅱ级)等精细化管理的城市则主要集中在经济水平较发达且相对距离较大、公共交通需求高、停运对社会经济的影响较大的城市(除崇左累计确诊人数为0)，以上数据截至2020-02-28；而停运城市支线(Ⅲ级)和分两阶段完全停运或一次仅保留少量线路(Ⅳ级)的城市主要根据本市病情扩散情况和城市所具备条件选择，分布规律性较弱。

全国各城市疫情爆发初期公共交通管控时间见表3。湖北省武汉和仙桃因疫情严重，在统计的第1 d便已实施公共交通全部停运的管控措施；而上海、广州、重庆、沈阳、北京、杭州等经济发达城市由于管控范围大、成本高等原因，实施交通管控时间较晚；崇左由于一直未出现确诊患者因而管控时间较晚；其他城市则根据本省政策，管控时间受本市确诊人数现状、经济水平、相对位置等因素影响，其管控时间基本集中在2020-01-25到2020-02-02。

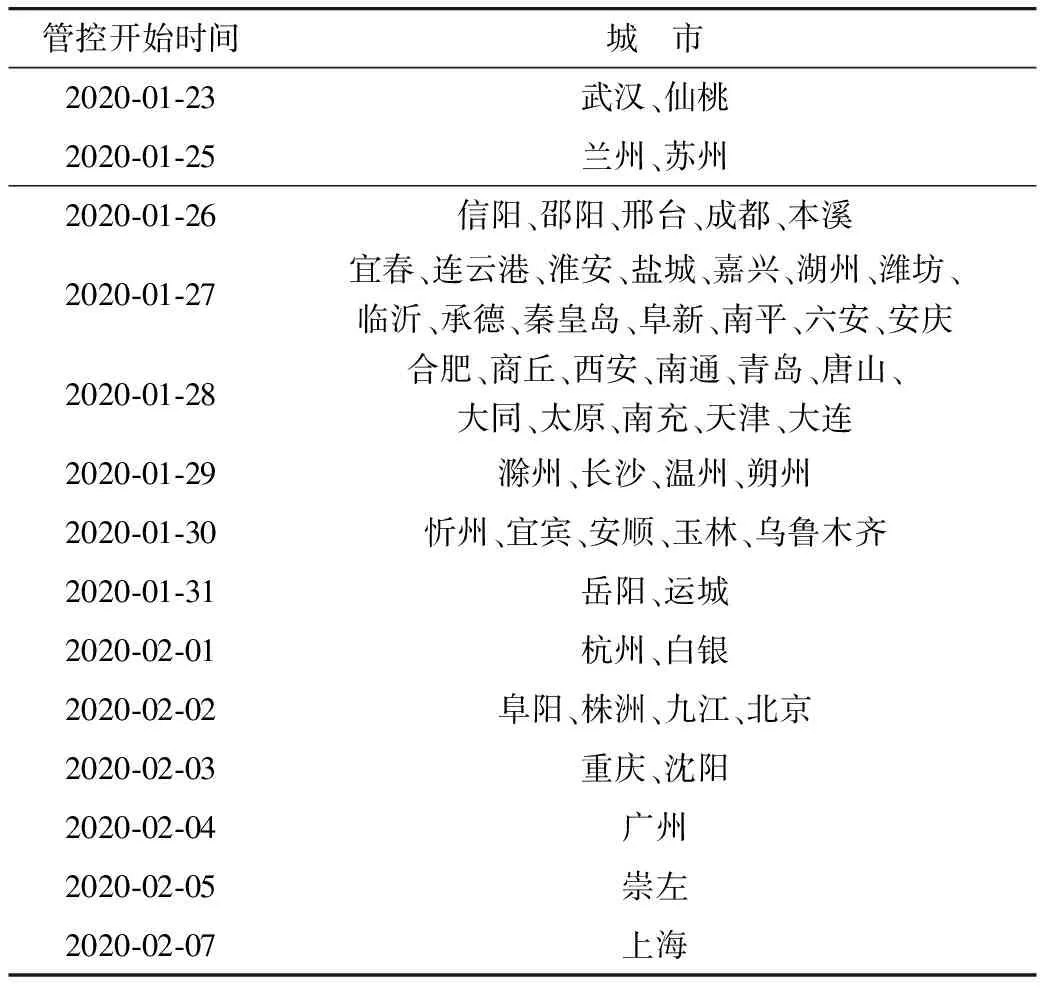
表3 疫情初期全国主要省市的城市交通管控开始时间

3 研究假设与分析方法

3.1 研究假设

病毒传播需要具备传染源、传染途径和易感染者这3个因素，故距离感染源越近的易感染者受感染可能性越大。此外，对于经济水平较高城市，其发达的公共交通在疫情期间为病毒传染提供了快速传播途径，因而经济水平、公共交通管控强度(以下简称管控强度)和公共交通管控及时性(以下简称管控及时性)也影响着病毒传播速度。笔者列出了因变量：最大累计确诊人数(Y)及4个影响因素：经济水平(X1)、相对位置(X2)、管控强度(X3)和管控及时性(X4)的参数定义和参数类型，见表4。

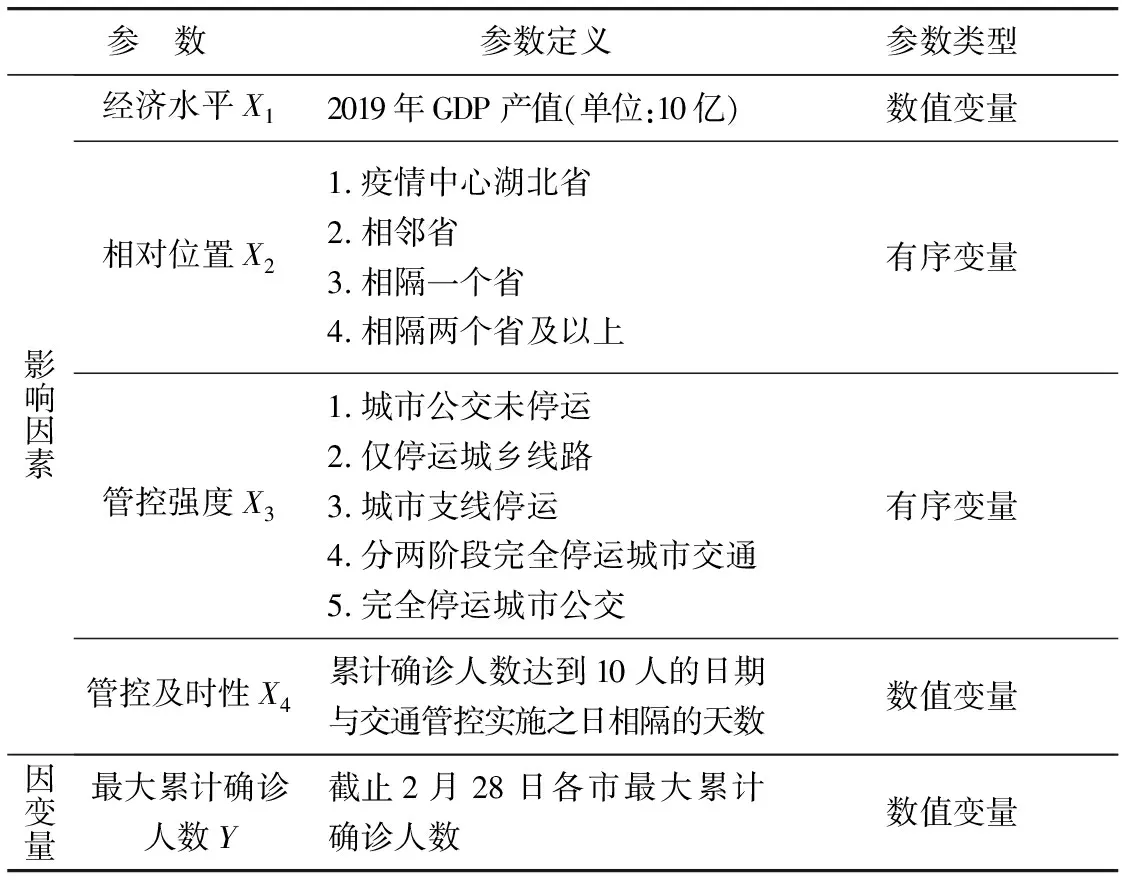
表4 变量定义

经济水平较高的城市由于外来人口多、人员流动量大、内部公共交通便利等特点，在疫情发生时为病毒传播提供了更为便利的条件；此外，邻近省市由于与武汉人员流通频繁，受疫情的影响也较大。基于此，笔者首先提出H01和H02两个假设：

H01：经济水平(X1)对新冠肺炎病毒(COVID-19)的最大累计确诊人数(Y)有正向影响；

H02：相对位置(X2)对新冠肺炎病毒(COVID-19)的最大累计确诊人数(Y)有负向影响。

公共交通因其密闭、容量大、集约型等特点在疫情爆发时成为病毒传播的高效途径，由此笔者提出管控强度越大越可有效减少最大累计确诊人数(H03)，管控及时性越高越可有效减少最大累计确诊人数(H04)两个假设：

H03：管控强度(X3)对新冠肺炎病毒(COVID-19)的最大累计确诊人数(Y)有负向影响；

H04：管制及时性(X4)对新冠肺炎病毒(COVID-19)的最大累计确诊人数(Y)有负向影响。

公共交通管控措施实施时间与该城市疫情严重性、管控对经济发展影响、公共交通依赖程度及国内国际影响等因素有关，因此管控及时性一方面反映了对疫情严重程度的预判，另一方面反映了管控及时性受经济、社会等诸多因素的羁绊。经济越发达，实施公共交通管控面临的压力就越大，管控准备措施越多，管控及时性越差，而较差的管控及时性又会引起累计确诊人数增多。因此笔者提出在经济水平与最大累计确诊人数的关系中，管控及时性具有中介作用(H05)。

H05：在经济水平(X1)与最大累计确诊人数(Y)关系中，管控及时性(X4)具有中介作用。

此外，在相同的管控及时性下，不同管控强度也会对累计确诊人数产生不同影响。当面临管控不及时情况时，可采取更高的管控强度来阻止病毒的快速扩散(如武汉)；若管控及时，则后期只需采取较低的管控强度(如湖州)。因此笔者提出管控强度在“经济水平→管控及时性→最大累计确诊人数”这一中介效应(H05)的后半段起调节作用(H06)，图1为模型结构。

H06：管控强度对“经济水平→管控及时性→累计确诊人数”这一中介效应的后半段起调节作用。

3.2 分析方法

3.2.1 典型相关性分析

典型相关分析(canonical correlation analysis, CCA)是多元统计分析的一个重要方法，能研究两组变量之间相关性，并有效揭示两组变量之间线性依赖关系。CCA是以两组变量相关系数最大为目标，将原始集合X、Y乘以映射系数投影为另一维数据U、V，然后计算U、V的相关系数，最后得到两者的相关性。

假设影响因素组X=[X1,X2, …,Xp]，因变量组Y=[Y1,Y2, …,Yq]为两组随机变量；Xi,Yj为一个长度为样本个数的向量，表示所有样本第i、j个元素的值；a=[a1,a2, …,ap]，b=[b1,b2, …,bq]分别为映射系数矩阵，即对应变量X、Y在U、V中所占权重，如式(1)～(3)：

(1)

U=a×X=a1X1+a2X2+…+apXp

(2)

V=b×Y=b1Y1+b2Y2+…+bqYq

(3)

∑11是X与X的协方差矩阵；∑12是X与Y的协方差矩阵；∑21是Y与X的协方差矩阵，也即∑12的转置；∑22是Y与Y的协方差矩阵。典型相关分析即是求两组变量系数矩阵a和b的相关系数，以使U、V之间的相关性达到最大，如式(4)：

(4)

最后可用式(5)、(6)进行显著性检验：

(5)

(6)

通过比较S2确定两组数据间是否存在系统误差。若F<95%时表明两组数据无显著差异，否则表明两组数据存在显著差异。

笔者首先采用典型相关分析，将两组变量之间的相关性转换成了两组典型变量之间的相关性，COV(U,V)即为所求的典型相关系数。

3.2.2 有调节的中介效应

中介效应是指变量之间的影响关系(X→Y)通过一个或一个以上中间变量(M)的间接影响产生的，因此称X通过M对Y产生的间接影响称为中介效应。中介效应是一种探究事物内在逻辑的方法，广泛应用于社会科学研究中。中介效应回归方程如式(7)～(9)：

Y=cX+e1

(7)

M=aX+e2

(8)

Y=c′X+bM+e3

(9)

式中：c为X对Y的总效应；a、b为中介效应(mediating effect)；c′是直接效应(a、b、c′的关系见图1)；中介效应之比ab/c，表示此中介效应占总效应的百分比。

调节效应是有因果指向的交互效应，调节变量一般不受自变量和因变量影响，但可影响自变量和因变量。以最简单的回归方程为例，调节效应检验回归方程包括式(10)、(11)：

Y=a+bX+cW+e

(10)

Y=a+bX+cW+c′WX+e

(11)

式中：W为调节变量；WX为调节效应，调节效应是否显著即是分析c′是否显著达到统计学意义上的临界比率0.05。

有调节的中介效应检验方法有：依次检验回归系数法、Sobel检验和Bootstrap法。由于Bootstrap法对样本量要求小、检验效力高、计算方便成为最主流的方法。笔者采用Bootstrap法：计算每个Bootstrap的中介效应估计值，从小到大依次排列，其中第2.5百分位和第97.5百分位点就构成了一个95%的置信区间，如果不包含0，则系数乘积显著。

4 分析结果

4.1 典型相关性分析

以经济水平(X1)，相对位置(X2)，交通管控强度(X3)和交通管控及时性(X4)为影响因素组，以最大确诊人数(Y)为因变量，在对数据中极端值删除后进行典型相关分析，结果如表5。

表5 典型相关性分析

由表5可知：影响因素组X与因变量Y的典型相关系数ρ=0.846，属于强相关，同时F值大于其临界值，P<0.001，说明影响因素组与被影响因素(累计确诊人数)之间的相关关系显著。在典型相关性分析中，各变量影响程度一般由因素在典型相关模型中系数绝对值来决定，若对应系数绝对值越大，那么该变量对因变量的影响程度就越高；影响方向由系数符号决定，正号表示正向影响，负号表示负向影响。由映射系数a可知，影响因素组X中系数绝对值排序中第1是经济水平(X1)为0.894、第2是相对位置(X2)为-0.565、第3时管控及时性(X4)为-0.096、第4是管控强度(X3)为-0.046。说明在影响因素组中，经济水平对累计确诊人数影响程度最高(正向影响)，其次为相对位置(负向影响)，再者是管控及时性(负向影响)，最后为管控强度(负向影响)。由此可见假设H01、H02、H03和H04均成立。

4.2 有调节的中介效应检验

4.2.1 自相关性检验

在进行有调节的中介效应检验前，首先应对自变量的自相关性进行检验，检验结果如表6。

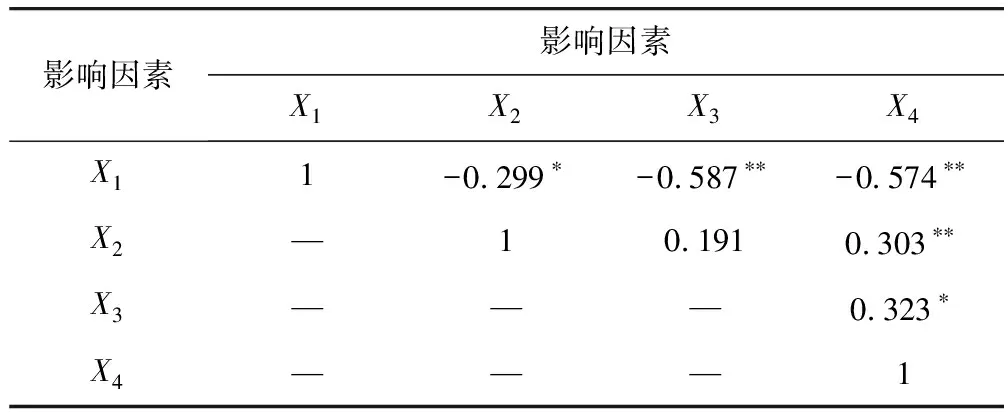
表6 自变量相关性检验

由表6可见：经济水平(X1)与管控及时性(X3)的相关性系数为-0.587，呈显著的负相关关系；与管控强度(X4)的相关性系数为-0.574，成显著的负相关关系。说明经济水平越高，管控及时性越差，管控强度越低。例如：表2中北京、上海、广东、浙江、江苏等经济水平较高的城市均采用了较低的管控强度，其中上海和北京在疫情爆发初期并没有停运公共交通。在管控及时性方面，北京、广州和上海的精细化公共交通管控实施都较晚，其中上海是2020-02-07才实施精细交通管控，是采取管控措施最晚的城市，说明交通管控的时间节点和强度的确定是个复杂的管理过程，越是经济发达地区，实施管控措施越谨慎，及时性也越差。

4.2.2 管控及时性在经济水平与最大累计确诊人数的中介效应检验

在管控及时性对经济水平与最大累计确诊人数的中介效应检验中，经济水平为前因变量，最大累计确诊人数为结果变量，管控及时性为中介变量。采用Bootstrap法进行5 000次抽样并取95%置信区间检验，其结果如表7、8。

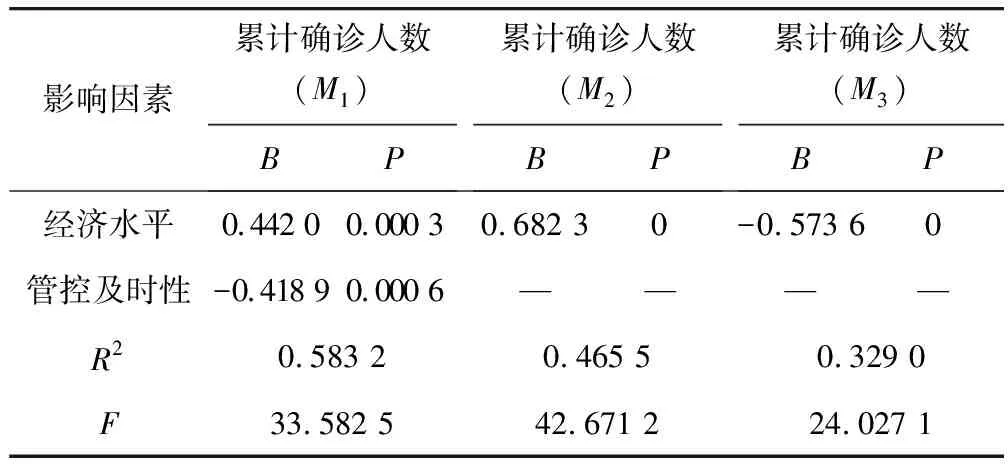
表7 管控及时性的中介效应检验

由表7的M2可知：经济水平对累计最大确诊人数的正向预测显著(B=0.682 3，P<0.001)。当放入中介变量后由M1可得：经济水平对最大累计确诊人数的直接预测作用依然显著(B=0.442 0，P<0.001)，管控及时性对最大累计确诊人数的负向预测作用也显著(B=-0.418 9，P<0.001)。由M3可得：经济水平对管控及时性的负向预测作用显著(B=-0.573 6，P<0.001)。假设H05成立，表明经济水平增加一个标准差，管控及时性减少0.573 6个标准差，累计确诊人数增大0.442个标准差。此外管控及时性减少的0.5736个标准差又会使得累计确诊人数增加0.240 3[(-0.573 6)×(-0.4189)]个标准差。最终表现为：经济增加一个标准差，累计确诊人数将增加0.682 3(0.442 0+0.240 3)个标准差。

由表8可知：经济水平对累计确诊人数直接效应及管控及时性的中介效应的bootstrap95%置信区间的上下限均不包含0，表明经济水平不仅能直接预测累计确诊人数，且能通过管控及时性的中介作用预测累计确诊人数。经济水平对累计确诊人数的总效应c=0.682 3，而经济水平对累计确诊人数的直接效应c′=0.442，经济水平通过管控及时性对累计确诊人数的中介效应a×b=0.240 3，即当经济水平增大一个标准差时，累计确诊人数将增大0.682 3个标准差，其中0.240 3个标准差是通过中介变量管控及时性对累计确诊人数起作用。而余下0.442个标准差则是经济水平直接对累计确诊人数起作用。中介效应占了总效应的35.22%(0.240 3/0.682 3)。例如以苏州和合肥为例，在现有经济水平不变基础上，若仅提前一天采取交通管控，则苏州累计确诊人数会减少10人，合肥累计确诊人数将减少12人，可见及时采取交通管控能非常有效的控制疫情。

4.2.3 管控强度在管控及时性对累计确诊人数影响中的调节效应检验

为进一步验证管控强度在管控及时性对累计确诊人数影响中是否存在调节效应，在上述中介效应中添加调节变量(管控强度)，其检验结果如表9。

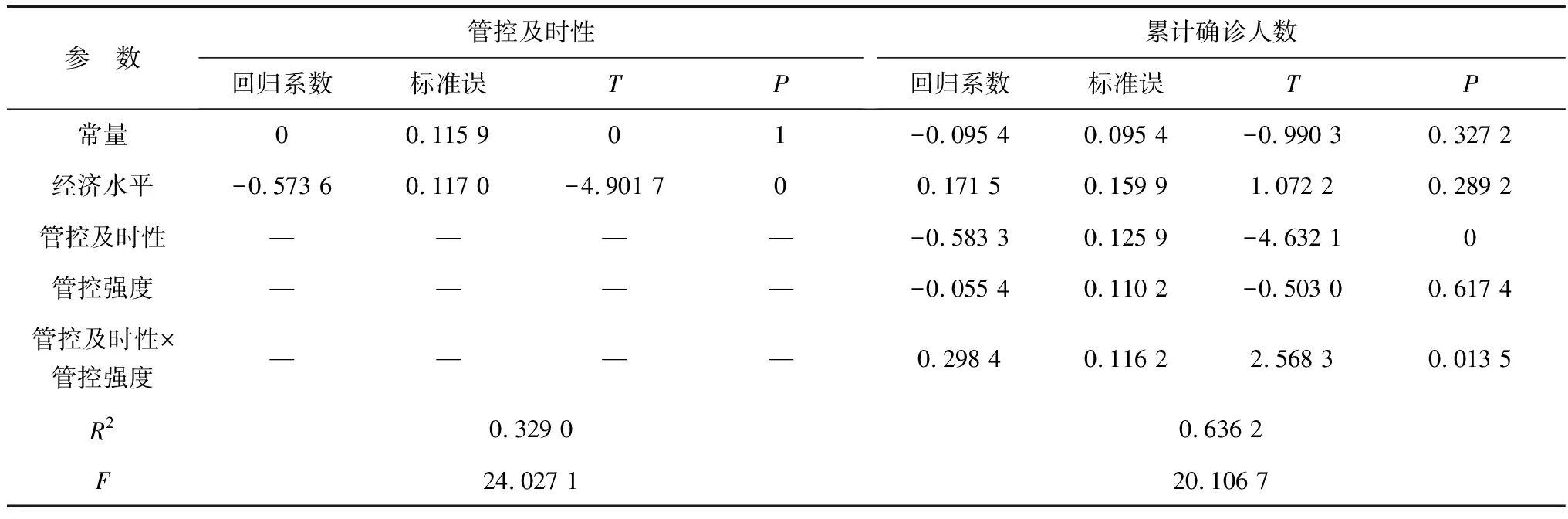
表9 有调节的中介模型检验

由表9可知：将管控强度放入模型后，管控强度与管控及时性的乘积项对累计确诊人数预测作用显著(T=2.568 3，P<0.05)，因此H06成立。此外，加入调节变量后R2由原本中介模型中的0.583 2(表7)上升为表9中的0.636 2，说明加入调节变量后拟合效果更好。

表10和图2对比了低管控强度和高管控强度时，管控及时性对累计确诊人数不同程度的预测作用。当管控强度较低(M-1SD)时，表10中95%的置信区间为[-1.304 8,-0.458 7]，图2中虚线的斜率为-0.881 7，说明经济水平通过管控及时性这一中介效应对累计确诊人数的具有显著的正向预测作用；当管控强度较高(M+1SD)时，表10中95%的置信区间为[-0.527 6,-0.042 1]，图2中实线的斜率为-0.284 9，说明经济水平通过管控及时性这一中介效应对累计确诊人数的正向预测作用较小。

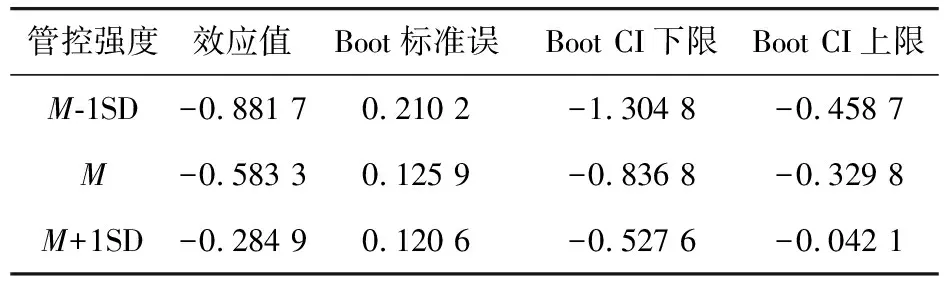
表10 在管控强度的不同水平上的中介效应

图2中无论是高管控强度还是低管控强度，调节作用的斜率均为负值(-0.881 7和-0.284 9)，说明无论是高管控强度还是低管控强度，累计确诊人数都随着管控及时性增加而减少。

在高管控强度下，及时管控(M+1SD)的累计确诊人数比不及时管控(M-1SD)的累计确诊人数减少了0.579 8个标准差；在低管控强度下，及时的管控(M+1SD)的累计确诊人数比不及时的管控(M-1SD)减少了1.773 4个标准差，远大于在高管控强度下管控及时性对累计确诊人数影响。

即随着管控强度提升，管控及时性对累计确诊人数预测作用呈逐渐降低趋势，效应值从-0.881 7变化到-0.284 9(表10)，说明高管控强度可弥补因管控不及时造成的大范围传染现象，若城市新冠肺炎传播已出现严重态势，则有必要采取更高强度的公共交通管控，如关闭公共交通或停运部分公共交通，这一措施比起低强度管控可减少约67.2%的感染者。

以江苏省苏州和安徽省合肥为例，在低管控强度下，管控及时性从M+1SD减小到M-1SD，苏州累计确诊人数将增加42人，而在高管控强度下，累计确诊人数将增加14人，减少了66.7%；同样，在低管控强度下，管控及时性从M+1SD减小到M-1SD，合肥累计确诊人数将增加116人，而在高管控强度下，管控及时性从M+1SD减小到M-1SD，合肥累计确诊人数只增加38人，减小了67.2%。由此可见，在高管控强度下，若及时采取公共交通管控措施，最多可减少67.2%感染患者。

5 结 论

笔者根据新冠肺炎(COVID-19)爆发初期全国56个城市的疫情相关数据，通过典型相关性分析和有调节的中介效应分析，研究得出经济发展水平、相对位置、管控强度、管控及时性对累计确诊人数的影响程度，并通过有调节的中介效应对各影响因素的内在逻辑进行梳理，得出如下结论：

1)经济水平、相对位置、管控强度和管控及时性与新冠肺炎(COVID-19)最大累计确诊人数均存在显著的相关关系。其中：经济水平对累计确诊人数的影响程度最高(正向影响)，其次为相对位置(负向影响)，再者是管控及时性(负向影响)，最后是管控强度(负向影响)。自相关分析结果表明：实施交通管控时间节点和强度是一个复杂的管理过程，经济水平越高，管理者实施公共交通管控措施越谨慎，管控及时性越差，管控强度越低；

2)通过中介效应分析发现：在经济水平对感染人数影响中，管控及时性起到了显著的中介效应(占比35.22%)。即经济水平对累计确诊人数影响中有35.22%是通过管控及时性这一中介变量产生的。由此可见，经济水平较高的城市通常会因公共交通管控影响较大，而无法及时采取交通管控措施，会出现不及时抑制疫情传播而导致确诊人数显著增加的结果。因此，对于经济水平发达城市，虽实施完全封闭的公共交通管制有难度，但可通过采取各种及时的对城市运行影响较小的精细化交通管控策略，降低其较高的疫情传播风险。

3)管控强度能对“经济水平→管控及时性→累计确诊人数”这一中介链条起显著调节作用。高管控强度可弥补因管控不及时造成的大范围传染现象。故当城市新冠肺炎传播已出现严重态势时，有必要采取更高强度的公共交通管控(关闭公共交通或停运部分公共交通)。在及时采取公共交通管控措施的前提下，实施高强度管控最多可减少67.2%的感染患者。

4)笔者仅搜集了新冠肺炎(COVID-19)在中国爆发初期的数据进行相关分析。未来将针对疫情稳定期、复工复产期，并结合国外疫情传播和相关管控数据进行定量分析，旨在为公共突发事件管控提供参考依据。