遗传算法优化支持向量机的城市交通状态识别

2020-08-24李巧茹郝恩强范忠国杨文伟

重庆交通大学学报(自然科学版) 2020年8期

李巧茹，郝恩强，陈亮，范忠国，杨文伟

(1.河北工业大学土木与交通学院，天津 300401；2.河北工业大学智慧基础设施研究院，天津 300401)

0 引言

城市交通状态识别不仅是现代智能交通系统(intelligent transport system, ITS)的重要内容之一，同时也是城市交通规划、设计和交通组织的重要依据。

交通状态识别具有主观模糊性，因此选取合理高效的算法判断交通状态是实现交通识别的关键。现有算法主要有：数理统计算法、聚类分析算法、模式识别算法。针对数理统计算法，A.R.COOK等[1]通过比较交通参数的实际观测值和双指数平滑法(DES)获得的预测值判断交通状态；B.N.PERSAUD等[2]提出了基于突变理论的McMaster算法，实现对交通拥堵类别的准确分类；M.LEVIN等[3]通过贝叶斯算法计算占有率变化的条件概率，实现交通状态的自动检测。针对聚类分析算法，任其亮等[4]通过建立交通参数之间的模糊相似性与样本之间欧式距离的映射关系，构建了基于遗传动态模糊聚类的交通状态判定方法；张亮亮等[5]考虑交通流参数在交通状态划分过程中作用的不同，提出了一种基于参数权重模糊聚类的交通状态识别方法；黄艳国等[6]提出了一种基于模糊C均值聚类的城市道路交通状态识别方法。针对模式识别算法，最具代表的算法为神经网络(neural network，NNet)算法和支持向量机算法，巫威眺等[7]提出了一种基于BP神经网络的交通状态判别算法，该算法在实测数据验证下具有较高的精确度和较好的收敛性；C.CORTES等[8]首次提出支持向量机模型，其在非线性和高维模式识别中也表现出许多优势；于荣等[9]利用支持向量机对道路交通状态进行分类；廖瑞辉等[10]针对拥挤预警信息的随机性和模糊性特点，利用支持向量机对交通状态进行判别，在预警系统取得成功。

综合分析现阶段国内外交通状态识别研究现状，数理统计算法、聚类分析算法以及模式识别算法已成为交通状态识别的重要手段。数理统计算法使用简便，但存在交通状态识别误报率高，实用性不强等缺点。聚类分析算法适用于交通状态识别的模糊性特征，但易于陷入局部最优以及对初始参数较为敏感，处理海量数据时存在一定弊端。神经网络模型简单，在处理并行数据方面具有天然优势，具备强大的非线性映射及反馈学习能力，但其易产生过拟合现象，在实际应用中效果并不理想。支持向量机具有严格的理论基础和数学基础，可避免局部最小问题，克服了神经网络算法过拟合的缺陷，且小样本学习具有较强的泛化能力。然而，支持向量机的分类性能对参数选择比较敏感，实际应用中存在依靠经验或试算方法确定参数的局限性，这在一定程度上限制了模型的泛化能力。吐松江·卡日等[11]提出了一种基于支持向量机和遗传算法的电力变压器故障诊断方法，该方法能准确、有效诊断变压器故障。

综上所述，本研究基于聚类分析算法，获取先验分类数据，并尝试采用遗传算法优化支持向量机参数模型，确定SVM最优参数组合，建立基于GA-SVM的城市交通状态识别模型，并在MATLAB平台下进行验证分析。

1 支持向量机

1.1 支持向量机分类理论

支持向量机是一种基于VC维理论和结构风险最小原理的模式识别算法，可根据有限样本信息在模型的复杂性和学习能力之间寻求最佳折中，进而实现模型推广能力的最优化。支持向量机在线性可分情况下，最优分类超平面定义的分类决策函数为：

f(x)=sgn[(w·x)+b]

(1)

(2)

(3)

(4)

(5)

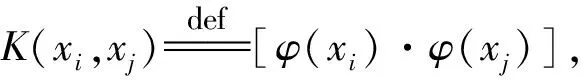
(6)

已有成果表明，目前应用较多的支持向量机核函数包括多项式核函数、径向基(RBF)核函数和Sigmod核函数3种，且在城市交通状态识别方面均有较好的应用效果。其中，径向基(RBF)核函数不仅能实现非线性映射，且参数较少，易于优化。因此选取径向基(RBF)核函数进行参数寻优。

1.2 支持向量机参数对其性能的影响

在支持向量机分类方法中，关键参数主要为惩罚系数C和核函数参数σ，其选择效果直接影响支持向量机的性能。

1)惩罚系数C影响模型的复杂度和训练误差。当C取值偏小时，样本数据中超出不敏感带的样本惩罚也偏小，同时训练精确度降低，系统推广能力变差，出现“欠学习”现象；当C取值偏大时，则易出现“过学习”现象。

2)核函数参数σ主要反映训练样本数据的范围特性，直接影响支持向量机模型的学习能力。当σ取值偏小时易出现“欠学习”现象，当σ取值偏大时易出现“过学习”现象。

由此可见，合理确定上述参数值能够有效降低支持向量机的训练误差，提高其学习能力。

2 GA-SVM交通状态识别模型

城市交通状态识别具有高度复杂性和主观模糊性等特点，虽然SVM模型在城市交通状态识别方面具有较好的应用效果，但在参数选择上依然存在依靠经验或者反复试验确定参数的局限性，影响SVM的推广能力。针对SVM模型中存在的问题，建立基于遗传算法优化支持向量机参数的城市交通状态识别模型。该模型分为3个部分，即城市道路交通状态分类理论和方法、遗传算法优化SVM参数、城市交通状态识别的GA-SVM模型。算法流程图如图1。

2.1 城市道路交通状态分类理论和方法

描述道路交通流整体特性主要有车流量、平均速度、占有率等参数指标。不同时段，城市道路交通流在这些参数下表现出不同的交通特性，据此建立三维指标评价体系，指标定义如下[12]：

1)车流量(pcu/h)：单车道2 min内各车型车辆数目之和，计算公式为：

(7)

式中：ni1为第1 min通过的第i类车的车辆数；ni2为第2 min通过的第i类车的车辆数；wi为第i类车辆的折算系数。

2)平均速度(mile/h)：单车道2 min内所有机动车的平均速度，计算公式为：

(8)

式中：v1为第1 min的平均速度；v2为第2 min的平均速度；f1为第1 min的流量；f2为第2 min的流量。

3)占有率(%)：单车道2 min内车辆在环形线圈检测器上的时间比例，计算公式为：

(9)

式中：ft为t时间段内的流量；lt为t时间段内所有机动车辆的车身长度；vt为t时间段内的平均速度；t为时间间隔，此处定义为2 min。

根据上述三维指标，对城市道路交通状态数据进行聚类分析，得到聚类中心矩阵为：

(10)

该矩阵第1列v1，v2，v4，v4分别代表顺畅流、平稳流、拥挤流、堵塞流的聚类中心；第2列代表车流量；第3列代表速度；第4列代表占有率。

2.2 遗传算法优化SVM参数

遗传算法种群规模设定为20，进化代数设定为200。保留精英遗传算法优化参数执行过程如下：

1)种群初始化。参数C和σ分别以n1和n2位二进制进行编码，则每组参数为一个基因长度n1+n2的二进制代码，如图2。

2)确定适应度函数。根据种群中个体得到SVM模型的初始参数值，用样本数据训练SVM模型，然后依据训练精确度确定个体适应度值，如式(11)～式(12)：

f=Ac

(11)

(12)

式中：f为适应度函数；Ac为预测精确度；N为训练总样本；Nf为错误分类的样本。

3)选择操作。采用遗传算法选择操作中的轮盘赌法。个体被选中的概率与其适应度值的大小成正比，这样就增加了个体的多样性，便于执行交叉操作和变异操作，如式(13)：

(13)

式中：fi为个体i的适应度值。

4)交叉操作。按照一定交叉概率交换配对个体基因，产生新的个体。第1代交叉后自适应概率如式(14)：

(14)

式中：G为遗传代数；Gmax为最大遗代数；Pc(1)为第1代交叉概率，此处定义为0.7；Pc(G)为第G代的交叉概率。

5)变异操作。按照一定的变异概率改变选中个体染色体的等位基因，增强种群的多样性。第1代变异后自适应概率如式(15)：

(15)

式中：Pm(1)为第1代变异概率，此处定义为0.01；Pm(G)为第G代的变异概率。

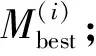
2.3 GA-SVM模型

将上述遗传算法进化过程中得到的最优个体分解为参数组合C*和σ*，代入SVM模型，得到城市交通状态识别的GA-SVM模型。在MATLAB平台下对GA-SVM模型性能进行测试分析。

3 MATLAB实验分析

3.1 数据采集与处理

岳麓大道为长沙市四横六纵的重要一环，承载着连接东西城区的重任。选取长沙市岳麓大道的实验路段西起涧塘立交桥，东至银盆岭大桥，道路线型大致呈直线线形，车道数为双向八车道，易于交通数据的采集。在车辆出行高峰期和低谷期，呈现多种交通状态。因此采集其周一至周五6:00—19:00的流量、速度和占有率数据，将城市道路交通状态设定为顺畅流、平稳流、拥挤流和堵塞流4种类别，进行聚类分析。每一种交通状态选用100个样本，共400组观测数据。取每种状态80个样本作为训练数据，20个样本作为测试数据，结果如图3、图4。其中，图3为交通数据的box可视化图，记录了样本数据分布情况，交通流参数属性正常，不存在异常点；图4为交通样本数据三维可视化图，在三维空间内呈现出4种交通状态，数据聚类效果明显。

3.2 仿真分析

在MATLAB平台下，利用LIBSVM工具箱对样本数据进行归一化处理，将数据归一化到[0,1]范围内。其中，图5为遗传算法迭代寻优过程，设定遗传算法种群规模为20，迭代次数为200。迭代寻优前期，适应度曲线随着迭代次数的增加，适应度逐渐上升；迭代寻优后期，适应度曲线趋于平稳状态，最佳适应度稳定在99.69%，说明在寻优过程中支持向量机参数种群不断进化，直到满足训练条件，获得最优参数C*和σ*。

图6为SVM测试集实际分类效果和预测分类效果对比图，结合现有研究成果设定C=2，σ=1，图中测试样本总数为80，准确预测样本数为76，Ac=95%(76/80)，错误预测的样本点为3个顺畅流样本点预测为平稳流样本点，1个拥挤流样本点预测为堵塞流样本点；图7为GA-SVM测试集实际分类效果和预测分类效果对比图，图中测试样本总数为80，最优参数组合C*=0.518 5，σ*=21.067 4，准确预测样本数为79，Ac=98.75%(79/80)，错误预测的样本点为1个拥挤流样本点预测为堵塞流样本点。

比较上述结果，GA-SVM模型和SVM模型均有较好的城市交通状态识别效果，其中GA-SVM模型比SVM模型识别精确度提高3.75%，具体结果如表1。

由表1可知，改进后的模型优于基于SVM的交通状态识别模型，主要体现在以下3个方面：①参数选取方法，参数C和σ的选择对支持向量分类机的学习和推广能力有很大影响，传统参数选取方法计算复杂，盲目性较强，利用遗传算法可以在初始化范围内对参数进行全局、快速搜索；②全局最优，遗传算法具有良好的全局搜索能力，不易陷入局部最优，利用遗传算法对支持向量机关键参数进行寻优，可找到使模型识别精确度更高的参数，在此基础上进行城市道路交通状态识别，更具科学性；③识别精确度，由表1可知，在测试集的识别分类中，GA-SVM模型识别精确度更高，更适于实际工程使用。