基于定量结构-性质关系预测含水二元共沸物的共沸温度与组成

曾行艳,诸 林*,吕利平,,李 兵

(1. 西南石油大学化学化工学院,成都 610500; 2. 长江师范学院化学化工学院,重庆 408100)

由于水具有安全、无毒、可再生能力强及溶解性能好的特点,被广泛应用于化工和医药等行业。在生产过程中,水和其他原料直接或间接的参与生产过程,会产生大量的含水共沸废液,如乙腈/水[1]、乙二胺/水[2]及四氢呋喃/水[3]等二元共沸物。 为了实现资源循环利用及环境保护的目的,需要采用特殊精馏对其进行分离。

共沸特性数据是分离工艺设计、模拟及优化的基础。 如果仅仅依靠实验来获取该类数据,会花费大量的时间和经济成本。 相比之下,状态方程法[4-5]、活度系数法[6-7]、经验法[8-9]以及定量结构-性质关系(QSPR)模型[10-11]等理论计算方法就具有简单、快速的特点。 目前,很多研究者利用理论计算方法预测了部分共沸物及混合物的相平衡数据,并取得了较好的效果[4,7-8,12-13]。 但是,前3 种方法在预测共沸物的共沸特性数据时,需要一些必要的实验参数或拟合参数,而通常这类参数的获取难度是比较大的。 QSPR模型具有计算量小、耗时短及精度高等优点,而且相关所需参数均可由分子结构计算所得,并不需要任何额外的实验数据,被广泛应用于化工等领域[14-17],如Liang 等从QSPR 中探索变压蒸馏过程设计和动态控制的关系,且利用QSPR 确定萃取精馏中溶剂对分离混合物相对挥发性的影响[18-20]。

基于此,本研究以125 种含水二元共沸物为研究对象,利用定量结构-性质关系分别构建可以高精度预测含水二元共沸物共沸温度及组成的QSPR 模型,以获取常压下该类共沸物的共沸特性数据;同时,也可为其他特殊种类二元共沸物共沸数据的预测提供参考和思路。

1 样本数据获取及分子描述符筛选

1.1 样本数据的获取

为保证所建的QSPR 模型不受数据源的影响,本文涉及到的125 种含水二元共沸物的共沸特性数据均选自溶剂手册[21]。 同时,本研究根据“Mixtures out”样本划分法[22]随机将整个数据集分为训练集(80%)和测试集(20%),以达到有效表征各类含水二元共沸物体系的目的,详见附件1 表1。 其中,训练集用于筛选特征描述符及建立QSPR 模型,测试集则用于评估所建模型的预测能力及泛化推广能力[13]。

1.2 分子结构的优化

常见分子结构绘制和优化软件有Symyx Draw、HyperChem、Gauss 和ChemOffice 等[15,23]。 本 研 究采用HyperChem 8.0 软件绘制和优化纯组分的三维分子结构以获取分子的最小能量构象。 相关优化步骤如下:先通过分子力学方法(MM+)预优化;再由量子力学半经验方法(PM3)进一步优化。 在优化过程中采用Polack-Ribiere 算法,且所有计算在Hartree-Fock 能级进行,至均方根梯度极限达到4.18×107kJ·m-1·mol-1[24]。

2 共沸温度及共沸组成QSPR 模型

2.1 分子描述符的筛选与模型构建

2.1.1 分子描述符的筛选

为准确的表征分子的结构特性,需要对分子描述符进行筛选,包括预筛选和进一步筛选,其筛选过程示意图如图1 所示。 本研究利用Materials Studio 8.0 软件计算纯物质的分子描述符,得到包括拓扑描述符、结构描述符及空间描述符等的15 类共344 种分子描述符;再以何培等选用的2 个基本原则[25]对其进行预筛选,以消除无用及冗余信息,减少共线性出现的概率,经预筛选后得到76 种分子描述符;再根据“Kay’s mixing rule”混合规则[26]计算得到二元共沸物的混合描述符,并采用遗传算法对其进一步筛选[27]。

2.1.2 共沸温度及组成模型的构建

经筛选后的混合描述符即可用于建立共沸温度及组成的QSPR 模型,模型的构建过程如图1 所示。 式(1)～(6)给出了不同混合描述符个数(4 ～9)的共沸温度预测模型,模型中的描述符以Ai表示;而式(7) ～(11)给出了不同混合描述符个数(2 ～6)的共沸组成预测模型,模型中的描述符以Bi表示,表1 列出了建模所涉及的全部描述符。

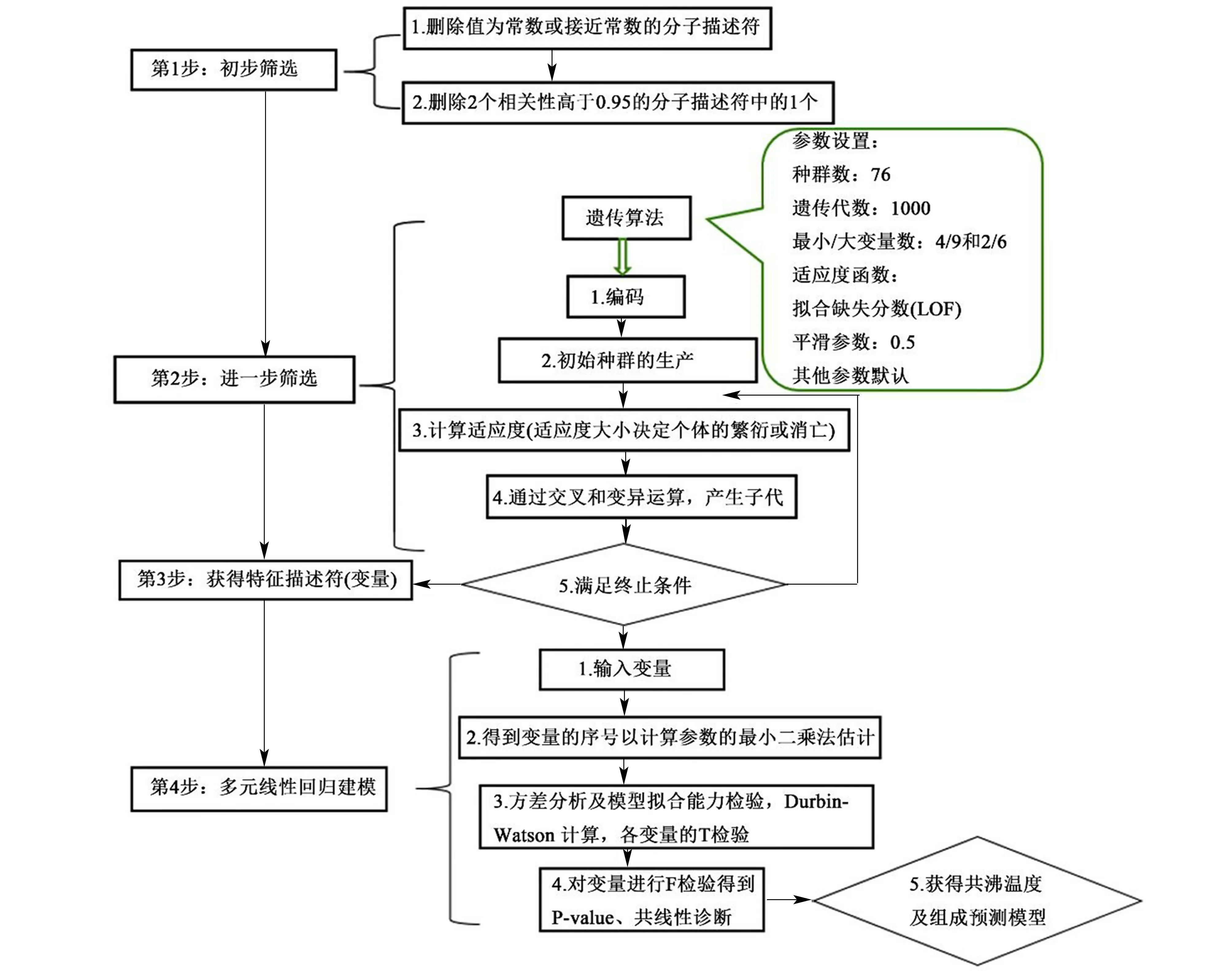
图1 特征描述符筛选及多元线性回归建模选示意图Fig.1 A schematic diagram of feature descriptor screening and multiple linear regression modeling

2.1.2.1 共沸温度模型

模型1:

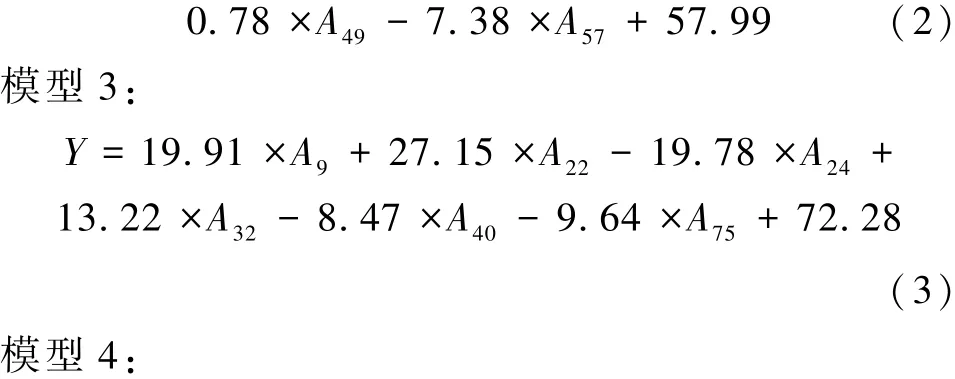
表1 共沸温度及组成预测模型构建所涉及的全部描述符Table 1 The descriptors involved in the establishment of the azeotropic temperature and composition prediction models

2.1.2.2 共沸组成模型

2.2 模型筛选

图2 和图3 分别为所建共沸温度及组成预测模型的复相关系数( R2),调整复相关系数( R2adj)和留一法交叉验证系数( Q2LOO)与混合描述符个数(n)的变化趋势关系图。 从图2 可以看出,当n 由4 增加到8 时,共沸温度预测模型的R2,R2adj和Q2LOO曲线稳健上升,而当增加第9 个混合描述符时3 个参数曲线均变得十分平缓,说明增加第9 个混合描述符对模型的拟合能力及稳定性提升不大。 从图3 可以看出,当n 由2 增加到3 时,共沸组成预测模型的R2,R2adj和Q2LOO曲线急剧上升;当n 由3 增加到5 时,3 个参数曲线缓慢上升;当增加第6 个混合描述符时参数曲线几乎没有变化;这说明增加第6 个混合描述符对模型的拟合能力及稳定性几乎不影响。由此可知,最适宜共沸温度及组成预测模型的最适宜描述符个数是8/5。

图2 共沸温度预测模型的描述符个数与R2,的关系Fig.2 The relationship between the number of descriptors and R2, of azeotropic temperature prediction models

图3 共沸组成预测模型的描述符个数与R2,R2adj, 的关系Fig.3 The relationship between the number of descriptors and R2,, of azeotropic composition prediction models

2.2.2 过拟合及显著性比较

拟合缺失分数(LOF)作为遗传函数算法的适度函数,其变化趋势可用于判断模型是否出现过拟合;而F 检验值的大小代表着方程的显著性,F 检验值越大则表明该模型的回归假设因果关系显著性越高。 图4 和图5 分别是共沸温度及组成预测模型的LOF 和F 值与混合描述符个数的关系图。 由图4可知,当n 由4 增加到8 时,LOF 值随n 的增加而快速下降,说明利用8 个特征描述符构建的模型不存在过拟合现象;而F 检验值随n 的增加有略微降低,但当n 增加到8 时,F 值也比较高(280.51),说明混合描述符数为8 时,共沸温度模型的回归假设因果关系显著性良好。 由图5 可知,当n 由2 变化到5 时,LOF 值随n 的增加先急剧下降随后逐渐减小,说明利用5 个特征描述符数构建的模型不存在过拟合现象,而F 检验值随n 的增加先快速增加随后在一定范围内波动,当混合描述符数为5 时,模型的回归假设因果关系显著性稍弱。 综上所述,利用8/5 个混合描述符所构建的共沸温度及组成预测模型不存在过拟合问题,且模型的假设因果关系显著性高。

2.3 最适宜模型分析

图4 共沸温度预测模型的混合描述符个数与LOF 和F 的关系Fig.4 The relationship between the number of mixed descriptors and the LOF and F of azeotropic temperature prediction models

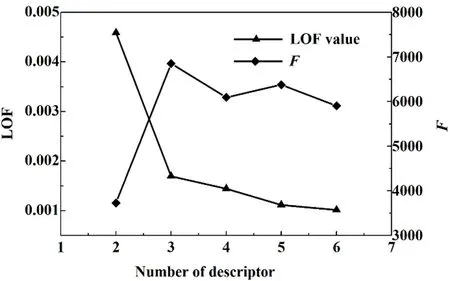
图5 共沸组成预测模型的混合描述符个数与LOF 和F 的关系Fig.5 The relationship between the number of mixed descriptors and the LOF and F of azeotropic composition prediction models

表2 给出了最适宜的共沸温度及组成QSPR 模型(模型5/模型10)的特征描述符(以下称之为变量)及统计学参数。 从表2 中可知,模型5 的8 个变量的标准系数分别为0.784、0.287、-0.235、0.184、0.156、0.097、0.150 和0.104,由 此 可 知 其 中 仅 有Chi (5): path/cluster 与共沸温度呈负相关;模型10的5 个变量的标准系数分别为- 0.131、0.252、0.457、0.497 和-0.118,由此可知其中Hydroxy 和Vertex adjacency/magnitude 描述符与共沸组成呈负相关,2 个模型各变量的具体数据如附件1 表2 和表3 所示。 此外,上述的13 个变量t-概率值均小于或等于0.005,说明这些变量对含水二元共沸物的共沸温度及组成的影响均是显著的。 模型5 和模型10 的R2和R2adj分别为0.960 6/0.997 0 和0.957 2/0.996 9,2 个模型的MAE 和RMSE 的值均较小,分别为1.890 0/0.010 4 和2.940 0/0.016 1,说明2 个模型分别对训练集共沸温度及组成的实验数据具有较好的拟合能力和预测能力。

图6 和图7 分别是变量对各QSPR 模型的影响占比情况。 从图6 可以看出模型5 的8 个变量对含水二元共沸物共沸温度的影响程度由大到小排序为:Hydrogen bond donor ＞Chi (4): path ＞Chi (5): path/cluster ＞Chi (4): path/cluster (valence modified)＞Complementary information content (CIC)＞Estate keys (indicators): I_sCH3＞Molecular shadow area fraction: ZX plane ＞E-state keys (sums): S_dO。从图7 中可以看出模型10 的5 个变量对含水二元共沸物共沸组成的影响程度由大到小排序为Structural information content (SIC)＞Complementary information content ( CIC) ＞Bond information content (BIC)＞Hydroxy＞Vertex adjacency/magnitude。

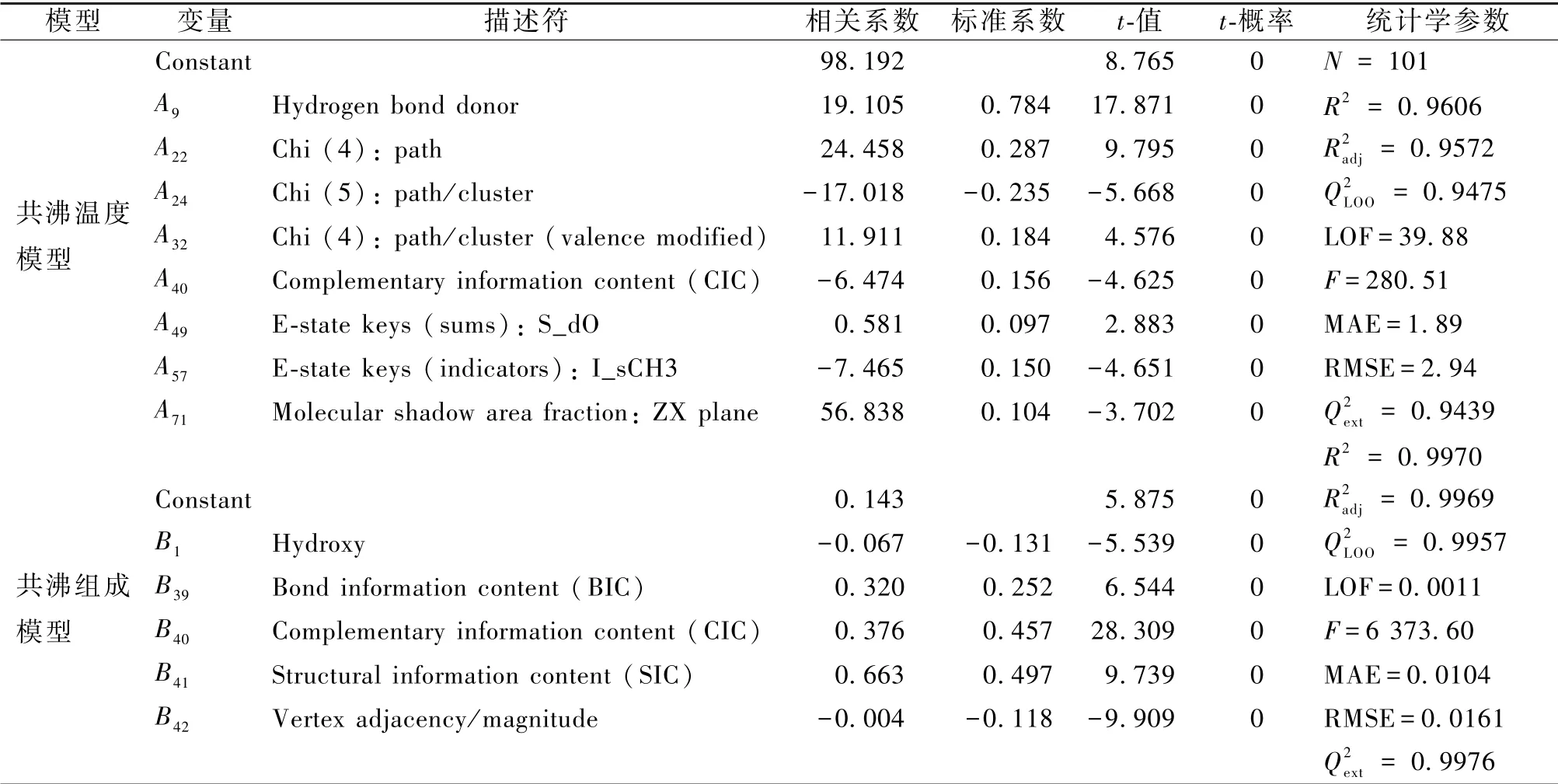
表2 最适宜的QSPR 模型的变量及统计学参数Table 2 The variables and statistical parameters of the optimal QSPR model

图6 特征描述符对共沸温度预测模型的影响Fig.6 Effect of each feature descriptors on the optimal azeotropic temperature model

2.4 模型验证

2.4.1 内部及外部验证

图7 特征描述符对共沸组成预测模型的影响Fig.7 Effect of each feature descriptors on the optimal azeotropic composition model

利用留一法交叉验证对模型的内部稳定性进行了分析,2 个模型的留一法交叉验证系数Q2LOO分别为0.947 5 和0.995 7,说明数据的拟合度良好,所建模型非常稳定。 在内部验证的基础上进行外部验证能进一步证明模型的真实有效性及外部预测能力,因此,本研究对测试集样本的共沸温度及组成进行了预测。 图8 和图9 是共沸温度及组成的实验值与预测值的关系图,从图8 和图9 中可以看出,2 个模型的测试集的预测效果和训练集的预测效果一致,散点均位于对角线附近,仅存在1 个共沸组成预测数据偏离对角线稍远,2 个模型的外部验证系数分别为0.943 9 和0.997 6,说明2 个模型的预测准确性高,泛化推广能力好。

图8 共沸温度的实验值和预测值的比较Fig.8 Comparison of experimental and predicted values of azeotropic temperature

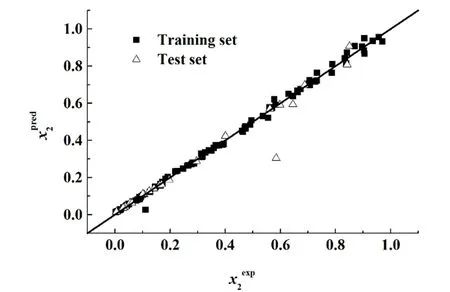
图9 共沸组成的实验值与预测值的比较Fig.9 Comparison of experimental and predicted values of azeotropic composition

2.4.2 残差分析

为了排除“偶然相关”的可能,需对2 个所建模型进行残差分析。 图10 和图11 分别是模型5 和模型10 的残差关系图,由图10 和图11 可知,2 个模型的计算残差均随机且无规律的均匀分布于基准线(0 线)两侧,说明在建模过程中均未产生系统误差。 同时,可以发现所有残差分布点均集中于基线附近,且大部分离基线较近,这也说明2 个模型的预测误差较小。

2.4.3 应用域分析

应用域分析最常用的方法是利用标准化残差和leverage 值作图,即Williams 图[26]。 图12 和 图13 分别是对模型5 和模型10 应用域分析的直观呈现图。 从图12 可以清晰的看出绝大部分样本落在该应用域以内,只有8 个样本落在应用域以外;由图13 可知,只有2 个样本落在应用域以外,另外有2 个样本落在边界线上。 究其原因可能是这类共沸物中有1 个分子的某些结构对于整个样本集来说比较特殊。 综上可知,最适宜共沸温度及组成模型具有较强的泛化推广能力。

图10 最适宜的共沸温度预测模型的残差与实验值的关系图Fig. 10 The Residuals versus experimental values of the optimal azeotropic temperature prediction model

图11 最适宜的共沸组成QSPR 模型的残差与实验值的关系图Fig.11 The Residuals versus experimental values of the optimal azeotropic composition prediction mode

图12 最适宜的共沸温度预测模型的应用领域的Williams 图Fig.12 Plot of Williams of AD of the optimal azeotropic temperature prediction model

图13 最适宜的共沸组成预测模型的应用领域的Williams 图Fig.13 Plot of Williams of AD of the optimal azeotropic composition prediction model

3 模型比较

将这2 个模型与同类文献模型及UNIFAC 基团贡献法进行比较,表3 列出了不同来源的共沸温度及组成预测模型的主要性能参数。 从表3 中可以看出,所建模型所涉及的变量个数与已有模型相近,但是本研究所建模型的R2和比其他QSPR 模型高,说明本研究所建模型的拟合能力和内部稳定性比其他模型高;从各个模型的外推预测效果来看,可以发现所建模型的远大于其他模型及UNIFAC 基团贡献法,且UNIFAC 基团贡献法对一些含水二元共沸体系存在无法计算的问题,即对所选数据集中的26 种二元共沸体系都未能计算出共沸温度及组成的预测值,表明所建模型的预测能力和泛化推广能力均优于现有模型,其预测结果数据详见附件1;从各个模型的RMSE 和AAE 来看,本研究所建模型的RMSE 和AAE 也远小于其他现有模型,这说明所建模型的预测精度高。 综上,可以看出所建立的模型不但拟合能力和内部稳定性有所提高,而且具备较强的预测能力和泛化推广能力。

表3 不同共沸温度及组成预测模型的主要性能参数Table 3 The main statistical parameters of QSPR model of azeotropic temperature and composition in different literatures

4 结论

本研究基于定量结构-性质关系探究含水二元共沸物的共沸温度及组成与分子结构之间的内在关系,对共沸温度及组成数据进行了预测。 得出以下结论:

1)经分子的三维结构绘制、优化,分子描述符的计算、筛选以及QSPR 模型构建与分析比较,确定最适宜的共沸温度预测模型和共沸组成预测模型分别是利用8/5 个特征描述符所建立的模型(模型5/模型10),2 个模型均具有方程显著性高、不存在过拟合、对实验数据具有良好拟合能力等优点,即含水二元共沸物的共沸温度及组成能被所建模型准确的预测。 模型5 和模型10 的F,LOF,R2,,RMSE 及MAE 分别为280.51/6 373.60、39.880 0/0.001 1、0.960 6/0.997 0、0.957 2/0.996 9、2.940 0/0.016 1 和1.890 0/0.010 4。

2)对2 个模型分别进行内部验证、外部验证、应用域分析,发现所建的2 个模型均具有较强的预测能力和泛化推广性能,其O和分别为0.947 5/0.995 7 和0.9439/0.997 6。

3)与同类模型和UNIFAC 基团贡献法相比,结果表明,本研究所建共沸温度及组成QSPR 模型对测试集样本的预测准确性和泛化推广能力均优于现有模型,可为工程上其他特殊种类的共沸特性数据的获取提供一定的参考和借鉴。