2024-O铝合金型材Ramberg-Osgood本构模型构建与方法研究

2020-08-20窦志家王东辉刘施洋

有色金属加工 2020年4期

窦志家，祝哮，孙巍，王东辉，刘施洋

(营口忠旺铝业有限公司，辽宁营口115000)

随着铝合金加工技术不断提升，材料数据库建立和数字化分析方法，在产品项目研发中的地位逐步凸显，也体现工业化技术底蕴与实力基础。常规的典型铝合金拉伸数据在计算机实际记录中具有一定波动且数据量庞大(图1)，导致无法对材料数据进行二次开发与使用。目前，在数字化分析使用中，通常以线性或者多线段方式，对线性和非线性段拉伸过程进行近似替代，使得在数字化分析弹性变形阶段过程具有较大失真。因此，材料数据处理是否科学及准确，则直接影响了材料及零部件等产品开发的准确性。本文通过对Ramberg-Osgood[1-3]方程模型构建，以满足数字化分析技术需求。

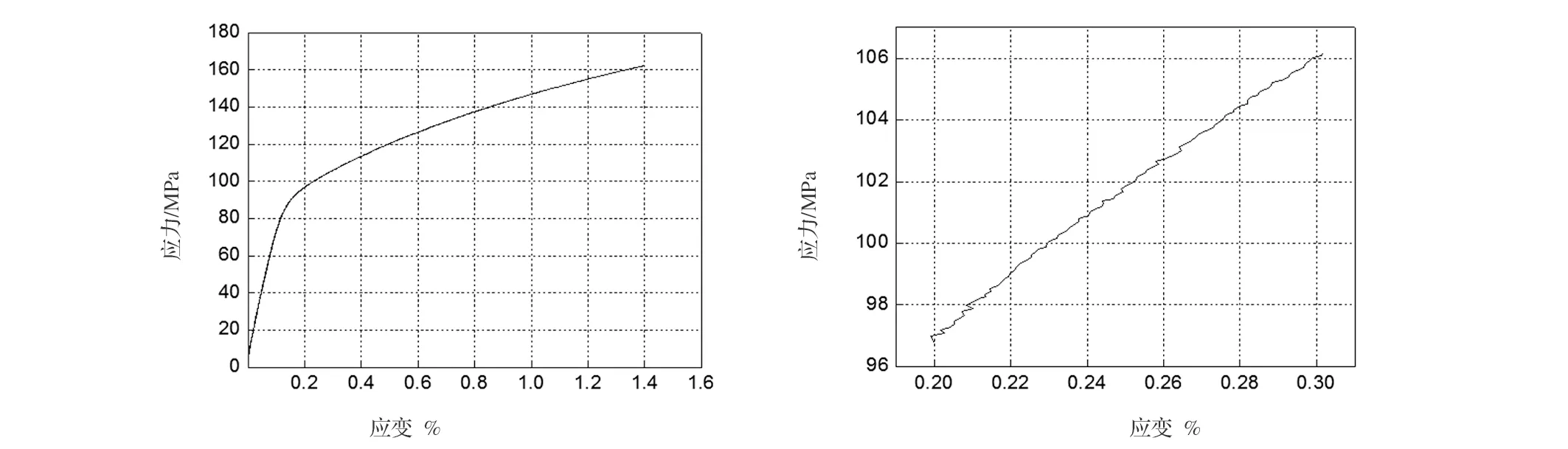
(a) 张力拉伸曲线部分 (b)张力拉伸曲线局部放大图1 拉伸曲线示意图Fig.1 Schematic diagram of tensile curve

1 试验方法

本文采用反向挤压2024铝合金型材，依照GJB 1694《变形铝合金热处理规范》相关工艺要求进行退火处理，退火设备采用Naberthem 1级均匀性热处理炉。

试样制备及试验过程依照国标要求[4]执行。试样采用日本岛津100KN万能材料试验机进行拉伸试验，为保证在试验过程中数据无因试验环境而导致奇异，在拉伸试验过程中采用定速拉伸，应变速率为0.0022mm/s，数据采集频率不低于95点/s。形成拉伸过程原始电子数据记录采用常规数据处理软件进行梳理及R-O模型建立。

2 Ramberg-Osgood方程建立与分析

Ramberg-Osgood模型是固体力学中提出形为ε=ε(σ)的模型，是描述材料连续光滑的应力-应变关系经典理论模型，其通用表达如式(1)所示。

(1)

式中，E为弹性模量；f为应力；fε0为惯用弹性极限强度；n为Ramberg-Osgood参数(后续简称为R-O参数)；其中，此处n与拉伸曲线的硬化指数为不同表征。

2.1 两点法建模

两点法建模是Ramberg-Osgood方程模型的一种传统方法，通过选取曲线上两个点的坐标值，带入式(1)中，通过联立方程求解即可完成模型建立。由于铝合金通常采用0.2%规定非比例延伸强度Rp0.2，则式(1)变为式(2)。

(2)

通过学者研究发现[5]，采用两点法建模形式简单，两个参考点选取多样。但由于参考点取值产品的微小波动，会对n取值范围和曲线形状具有一定的影响。以取0.1%规定非比例延伸强度Rp0.1为第二参考点为例，结合式(2)，R-O参数n则可通过式(3)进行计算。通过对同一批次2024-O多组数据计算Rp0.2/RP0.1取值范围为[1.092，1.097]，n的取值范围为[7.48，7.87]，均值为7.7。

(3)

通过R-O不同指数绘制曲线与原始拉伸曲线比较如图2所示。可以看出，采用两点法构建的2024-O的Ramberg-Osgood方程模型，在非线弹性低应力区域与原始曲线具有一定差异，且强度及比例极限值均小于原始数据。由于曲线必通过屈服点，因此随着应变量增加强度差异逐渐缩小。过屈服之后模型数据值与原始数据差异逐渐增加。

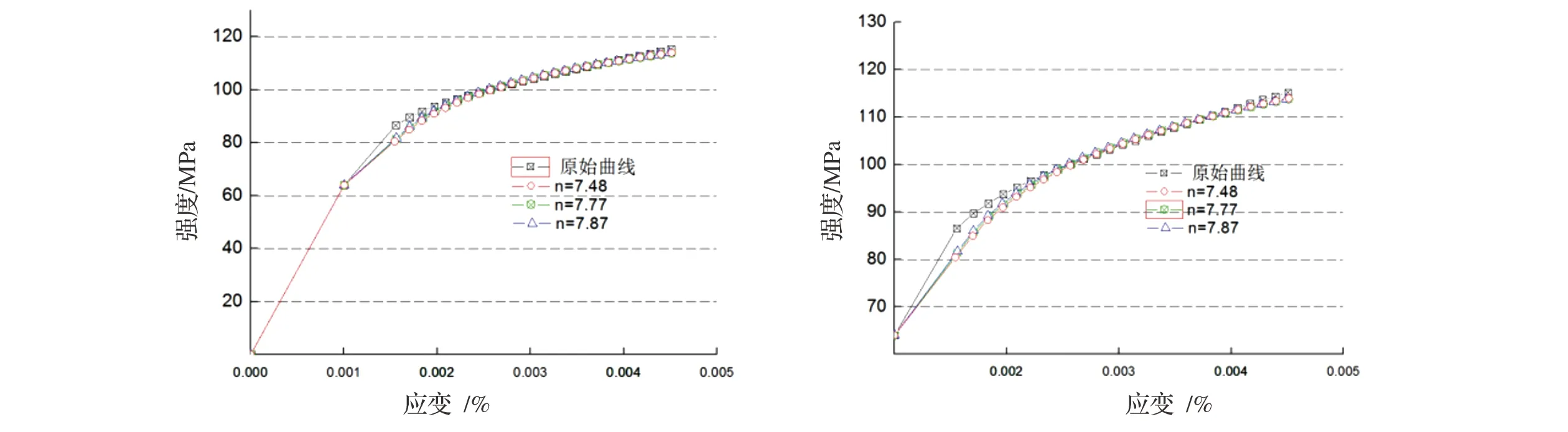
(a)整体曲线 (b)非线弹性至塑性变形曲线图2 两点法不同R-O参数n值曲线差异Fig.2 Curve difference of different R-O parameter n-value by two-point method

2.2 最小二乘法

由于Ramberg-Osgood方程模型为幂函数，因此通过方程进行对数转换形成线性关系式，再通过最小二乘法[6]对线性关系式进行线性拟合，方程经转换后如式(4)所示。

Y=b+x/n

(4)

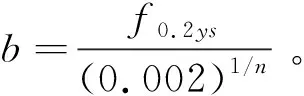
采用最小二乘法所需数据采取过程如图3所示。通过不同的规定非比例延伸强度比，参照国标的逐步逼近法获得比例极限强度至某点塑性强度的多点强度及应变数据对，并进行曲线拟合及Ramberg-Osgood方程模型的建立。

根据图1(b)和图3可知，在非线弹性的初始阶段，此处曲线曲率变化较快，若数据采集间隔较小，则在计算时易受到图1(b)所示采集数据波动影响，在非线弹性低应变处求得错误的应力结果。若数据采集间隔较大，即采集相对较少的数据对进行计算，则R-O参数n有可能因为数据量问题对方程建立产生影响。因此，对同一试样的参与不同数量数据拟合点总数对R-O参数n影响如图4所示，可以看出随着拟合数据点增多，R-O参数略有降低并趋于稳定。因此，拟合数据越多参数n值越准确，但为减少数据运算时间，参与拟合数据量取至10个以上即可。

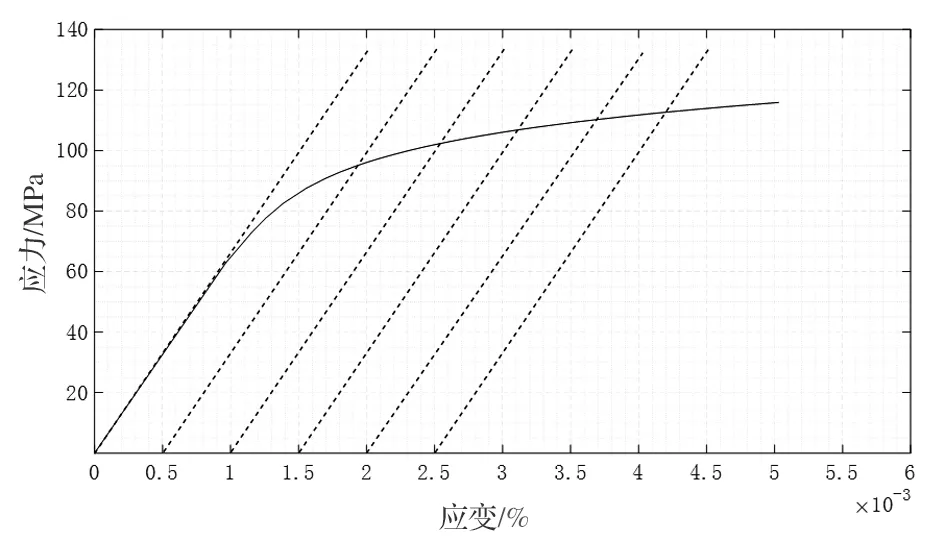
图3 最小二乘法数据获取示意图Fig. 3 Schematic diagram of least square data acquisition

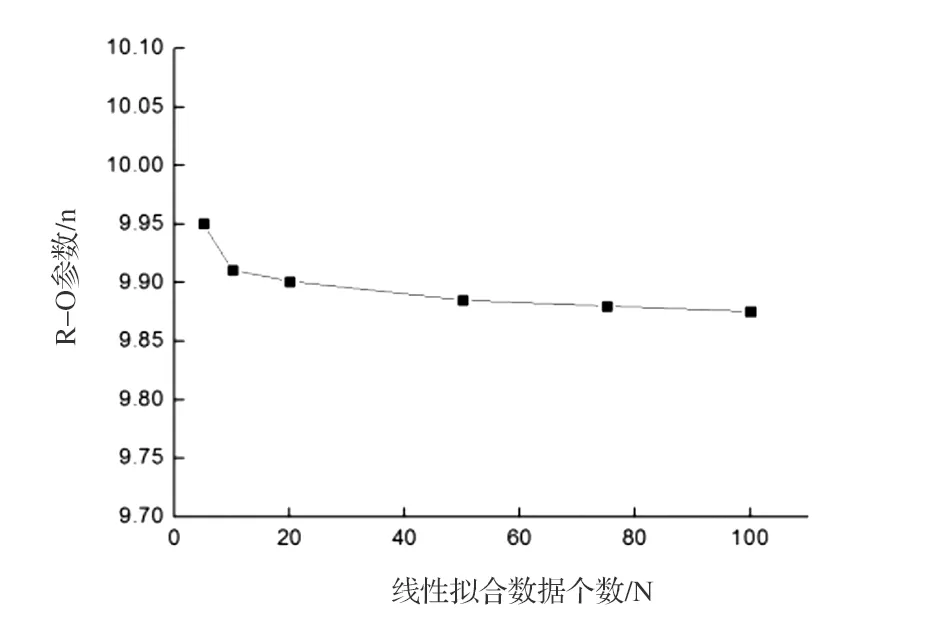
图4 线性拟合数据个数对R-O参数n影响Fig. 4 Influence of linear fitting data on R-O parameter n

通过最小二乘法2024-O的R-O参数n值在[9.88，9.94]，与原曲线比对如图5所示。

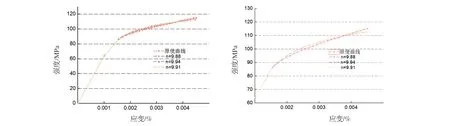
(a)整体曲线 (b)非线弹性至塑性变形曲线图5 最小二乘法不同R-O参数n值曲线差异Fig. 5 Curve difference of different R-O parameter n-value by least square method

通过曲线可以看出，非线弹性随着应变量逐渐增加，R-O形成的拉伸曲线与原曲线相比，差值先增加后降低，且Ramberg-Osgood方程形成强度数值在同等应变下略高于原始曲线，到屈服强度点处完全重合。

2.3 方法比较

通过两点法和最小二乘法均可获得Ramberg-Osgood方程，但通过两种方法结果可以看出,采用两点法计算指数与最小二乘法指数具有一定差异。在相同应变量下，两种方法与原曲线比对结果如表1所示。

表1 两点法和最小二乘法与原曲线差异比对结果

通过表1、图2和图5可知，采用最小二乘法获得的Ramberg-Osgood方程与原曲线符合程度比较好。这是由于采用最小二成法时，考虑了非线弹性阶段整体的应力与应变关系，从而使方程与原曲线具有良好的符合性。而不像两点法，方程建立主要取决于第二点选用的位置，0.1%规定非比例延伸强度进行计算，使得0.1%～0.2%处与原曲线较为接近，但从比例极限至0.1%处与原曲线具有一定偏移。