层次分析法在大型信息系统试验选址中的应用

潘忆江

(中国电子科技集团公司第二十研究所，陕西 西安 710068)

0 引言

随着我国海军建设的逐步发力，海军大型信息系统的研制也在逐步开展[1]。在大型信息系统研制过程中，为节约成本，提前释放研制风险，需组织传感器、通信、导航、指控等大型信息系统所辖的分系统或设备，开展陆上集成联调试验及定型试验工作，这其中涉及到试验选址问题。陆上试验选址是试验开展的前提，是确保在合理费用下达到试验目标的关键因素之一[2]。在大型综合系统陆上试验选址中，试验选址分为初期调研和选址方案两个阶段。初期调研是对预选地区的地形、环境、保障条件进行考察，筛选出符合技术条件、保障条件和环境条件要求的小区域的过程。选址方案则是在此基础上，对各个试验站点进行优化配置，选择更有利于达到试验目的并提高试验效费比的过程。由此可见，大型信息系统陆上试验选址涉及的因素较多，各因素间的关系错综复杂，在选址方案阶段，为优化配置选址更有利于达到试验目的并提升效费比的方案，需建立一套试验选址方案的评价体系[3]，并在诸多备选方案中选出最为科学的方案。因此该问题可视为一个复杂的多目标决策问题，为解决该问题，本文提出了利用层次分析法，建立大型信息系统试验选址的层次结构模型及权重表，通过模糊综合评价法，确定最科学合理的试验选址方案。

1 层次分析法及模糊综合评价法

1.1 层次分析法

20世纪70年代，美国运筹学家T.L.SAATY教授提出了层次分析法[4]，该方法是结合定量分析和定性分析的一种系统工程分析方法，其将一个复杂的多目标决策问题看做一个总目标，并将这个总目标逐层分解，分解成为数个子目标或多个指标、多个准则等，通过多个层次的分解，构建一个有序的层次结构，即层次结构模型。构建完成层次结构模型，依据相对重要性对模型内的各个要素进行两两比较，得出相对应的权重数和总排序，从而对复杂的多目标决策问题进行优化决策。

1.2 模糊综合评价法

模糊综合评价法[5]是以模糊数学的思想为基础，对不易明确界定的问题进行综合评判的一种决策方法。针对不易明确界定的问题，该方法认为其为模糊对象，并建立囊括该对象各个性质的模糊概念的集合，利用隶属度函数理论对该集合的定性分析转化为定量分析，完成对该问题的总体评价。通过该方法可将复杂的多目标决策问题做出科学的总体评价，从而解决复杂的多目标决策问题不易分析的问题。

2 大型系统试验选址的层次结构模型

要建立大型系统试验选址的层次结构模型需综合考虑试验选址涉及因素繁多，并将其按照属性划分为若干个有层次性的元素[5]。构建的大型系统试验选址的层次结构模型如图1所示。大型信息系统陆上试验选址需要考虑三个条件，分别是技术条件、保障条件和环境条件。

2.1 技术条件

技术条件是确保试验内容顺利进行的必要条件，试验选址若不能满足试验正常开展的技术条件，将直接导致试验失败。试验技术条件根据试验内容可进一步分为站点阵型条件、传感器设备使用条件、通信设备使用条件、导航设备使用条件和目标空域飞行条件，各个条件分别确保相关试验内容的顺利开展。

2.2 保障条件

保障条件是试验顺利开展的必要前提，为试验提供各种后勤供给。为了确保试验设备顺利进场，需考虑交通运输保障条件；为确保试验设备正常运转需考虑水电能源保障条件；为确保参试人员的正常生活，需考虑人员保障条件；试验开展离不开试验场所，需考虑基础建设保障条件；上述所有条件都离不开经费的支撑，因此还需考虑经费保障条件。

2.3 环境条件

环境条件是试验正常开展的必要因素，特殊的试验项目需要特定环境条件予以配合。综合分析环境条件，可分为电磁环境条件、地质条件、气象条件和水文条件，各条件综合影响试验设备运转，左右试验开展的过程，在一定程度影响试验结果。

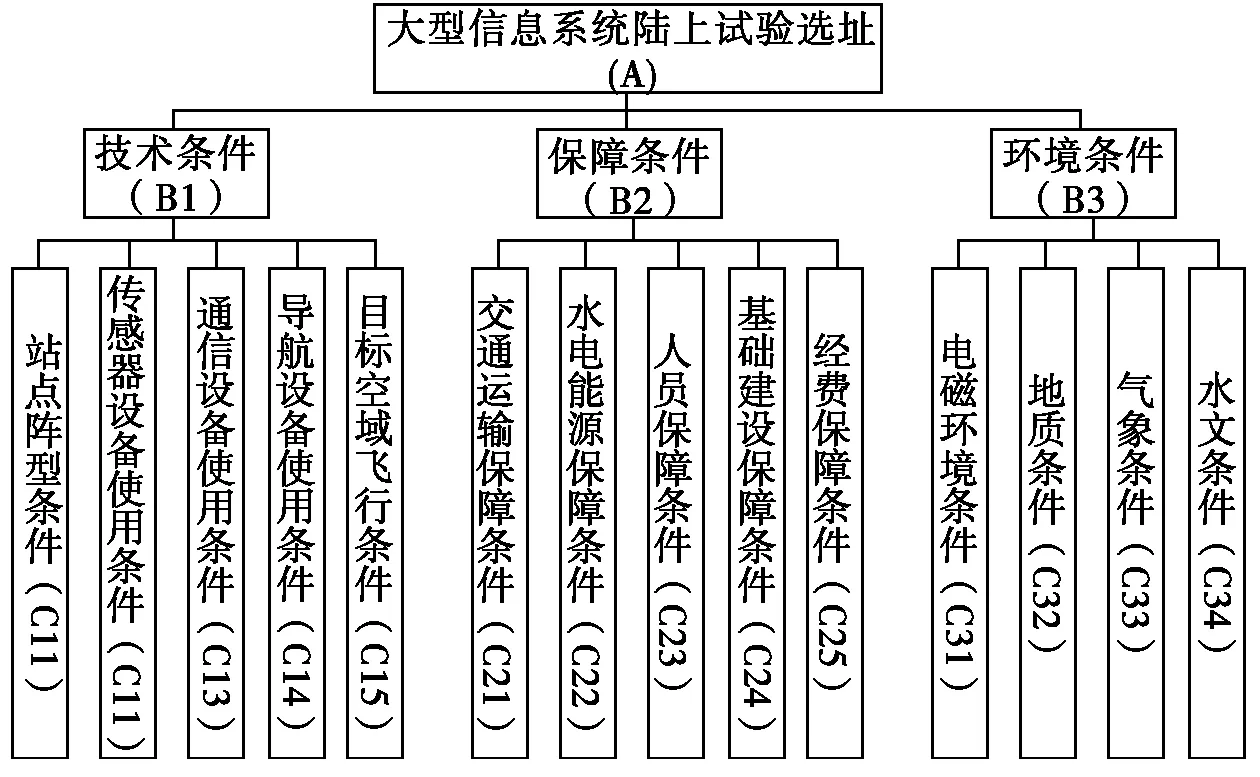
图1 大型信息系统陆上试验选址的层次结构模型

3 应用实例

以大型信息系统陆上试验选址为例，通过初期调研，依据试验开展的技术要求，对预选地区的环境、保障条件进行实地调研和综合分析，确定三个备选的试验选址地点，分别是S省的试验地址D1、J省的试验地址D2和D3。

3.1 建立判断矩阵

根据第2节中的大型信息系统陆上试验选址的层次结构模型，项目组对各个条件进行两两比较，对每个层次中的每个条件因素进行判断，构造出判断矩阵。在两两比较时，各个因素的重要程度需定量赋值。为了能充分刻画重要程度的差别，两两比较的结果划分为9个程度，当取值为程度1时，表示因素1和因素2一样重要；取值为程度5时表示因素1比因素2明显重要；取值为9时表示因素1比因素2绝对重要，重要程度依次递增。

根据上述两两比较的重要程度赋值，项目组对大型信息系统陆上试验选址的层次结构模型中的各个层次进行了比较，其中大型信息系统陆上试验选址(A)的判断矩阵为：

技术条件(B1)的判断矩阵为：

保障条件(B2)的判断矩阵为：

环境条件(B3)的判断矩阵为：

3.2 建立相对权重表

ωA=[0.6483 0.1220 0.2297]
λmax=3.003 7
CI=0.001 8<0.10

通过一致化检测。同样，技术条件(B1)的权重：

ωB1=[0.0753 0.1588 0.3638 0.0383 0.3638]
λmax=5.197 5
CI=0.049 4<0.10

通过一致化检测。保障条件(B2)的权重：

ωB2=[0.0646 0.2504 0.1315 0.5177 0.0357]
λmax=5.349 2
CI=0.087 3<0.10

通过一致化检测。环境条件(B3)的权重：

ωB3=[0.5638 0.1178 0.2634 0.0550]
λmax=4.134 8
CI=0.044 9<0.10

通过一致化检测。

根据判断矩阵，对各个层次的权重进行排序，依据上一层次的权重计算下一层次的权重值，结合层次结构模型，建立相对权重表，见表1。

3.3 模糊综合评价

项目组各个成员根据层次结构模型，分别对备选的试验选址地点D1、D2和D3进行评价，由1-9进行打分，9为最好，1为最差，得到技术条件(B1)的评价矩阵：

保障条件(B2)的评价矩阵：

环境条件(B3)的评价矩阵：

利用评价矩阵和相对权重表综合计算出D1、D2和D3选址的综合评价值为5.9449、3.8754、5.0978，因此D1的综合评价最好，选择该备选选址最为合适。在某某大型信息系统陆上试验中，最终试验选址也是选址的D1备选选址。

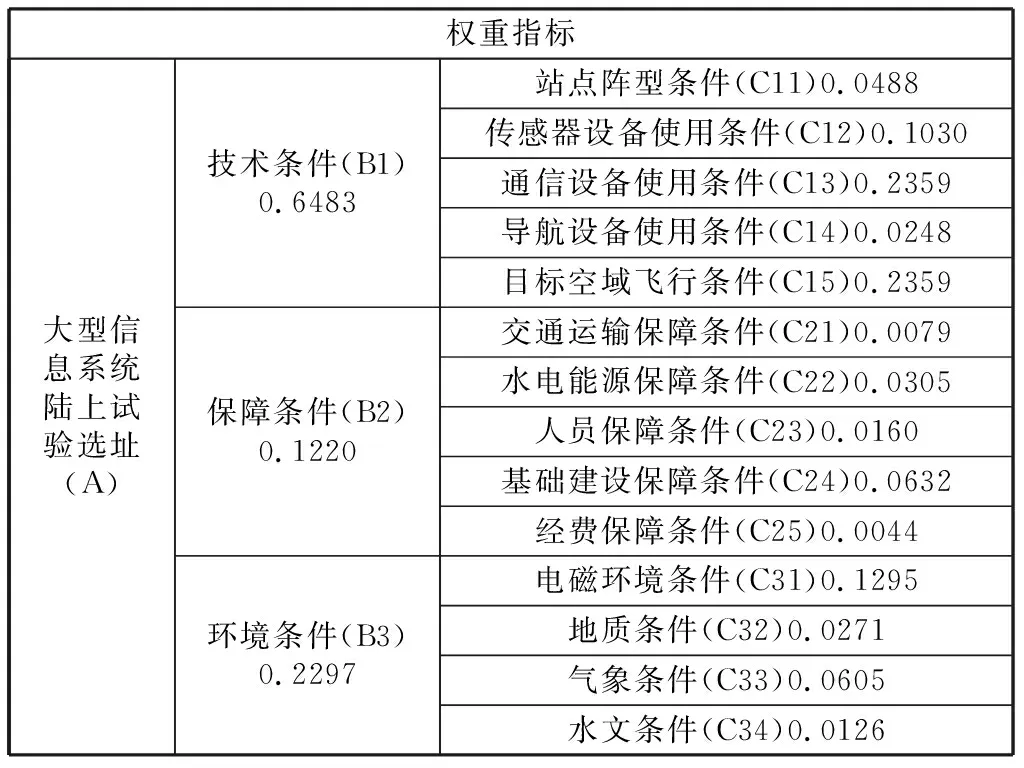
表1 相对权重表

4 结语

通过利用层次分析法和模糊综合评价法，科学合理地解决大型信息系统陆上试验选址问题。本文利用该方法，建立了大型信息系统陆上试验选址的层级结构模型，项目组依据这个层级结构模型建立了相对权重表，并开展了模糊综合评价，利用该方法在某大型信息系统陆上试验中验证了该方法的合理有效。