柔性悬臂结构极点配置阻尼设计与振动控制

程智 潘颖 张婷 刘彬

摘 要：随着航天航空技术的发展，航天航空等领域内智能结构的运转强度与工作精度的要求达到了新的高度，由于柔性悬臂结构自身存在结构阻尼特性，影响系统稳定的输出状况，大程度地缩短其使用周期。为研究柔性悬臂结构的振动特性，以智能悬臂梁结构为研究对象，首先通过动力学方程分析悬臂梁振动特性，压电陶瓷片力矩方程结合振型叠加法推导出四阶模态的悬臂梁振动微分方程，并用ANSYS有限元验证模型的正确性，然后运用极点配置控制算法给定智能悬臂梁结构初始位移激励使其做自由振动，采集位移信号作为输入来产生相应的控制电压抑制智能悬臂梁结构的自由振动，并通过仿真和实验证明极点配置控制算法的可靠性。结果表明：数值仿真中，输入信号为6 mm时，智能悬臂梁结构输出位移能够在5 s内迅速衰减保持在合理范围，控制电压也在5 s内趋于稳定;实验分析中，在初始位移激励为6 mm时，智能悬臂梁结构输出位移响应在6 s内迅速衰减保持在合理范围，其控制电压也在6 s内趋于稳定;数值仿真和实验分析的结果基本一致表明了极点配置控制算法能够切实有效的控制智能悬臂梁结构的自由振动。关键词：智能结构;多阶模态;极点配置控制;振动控制中图分类号：TP 29

文献标志码：A

文章编号：1672-9315（2020）06-01081-07

DOI：10.13800/j.cnki.xakjdxxb.2020.0619開放科学（资源服务）标识码（OSID）：

Damping design and vibration control of flexible

cantilever structure pole placement

CHENG Zhi1，PAN Ying1，ZHANG Ting1，LIU Bin2

（1.College of Mechanical and Automotive Engineering，Shanghai University of Engineering Science，Shanghai 201620，China;

2.Xian Satellite Control Center，Xian 710043，China）

Abstract：With the development of aerospace technology，the operation strength and working accuracy of intelligent structure have made great progress in aerospace and other fields.Due to the modal damping characteristics of flexible cantilever structure，the stable output of the system is affected，with its service cycle  greatly shortened.To investigate the vibration characteristics of flexible cantilever structure，intelligent cantilever beam structure is taken as the research object.Firstly the dynamic equation is used to analyze the dynamic characteristics.The piezoelectric ceramic chip torque equation is combined with the modal superposition method of fourth order modal to ratiocinate the dynamic differential equations，and use ANSYS finite element model is proved to be correct using ANSYS，and then using the pole placement control algorithm for a given initial displacement excitation to do intelligent cantilever beam structure free vibration，collect displacement signals as the input to generate the corresponding control voltage suppression intelligent free vibration of cantilever beam structure，and the simulation and experiment prove  the reliability of the pole placement control algorithm.The results show that：in the numerical simulation，when the input signal is 6mm，the output displacement of the intelligent cantilever beam structure can rapidly attenuate within a reasonable range within 5 s，and the control voltage tends to be stable within 5 s.In the experimental analysis，when the initial displacement excitation is 6 mm，the output displacement response of the intelligent cantilever beam structure rapidly attenuates within a reasonable range within 6 s，and its control voltage tends to be stable within 6 s.The results of numerical simulation and experimental analysis show that the pole placement control algorithm can effectively control the free vibration of intelligent cantilever beam.

Key words：intelligent structure;multimode;pole placement control;vibration control

0 引 言

随着智能结构在航天航空方面的广泛应用，反应灵敏且驱动控制效果良好的智能结构振动控制方面的研究也愈发重要[1-2]，除了在振动方面的研究智能结构还具有检测与健康评估的作用，对外界环境的敏锐感知和探测使得智能结构对外部结构运行状态进行评估，进而做出准确的判断，在通信工程、资源探测、生命体征等其他领域也有着重大的参与[3]。但智能结构的在运行过程中的振动特性影响了系统的的反应速度，输出结果延时造成系统不能在第一时间做出控制效果，影响控制精度[4]。

常见的智能结构有压电陶瓷片与悬臂梁运动结合[5-6]，且在振动过程中存在多阶模态，各阶模态的固有振动特性各不相同，实际的振动状态可根据各阶的主要模态判断，并设计相应的振动控制器[7-9]。振动阻尼的存在有助于减小振动位移，YANG等提出的双稳态压电悬臂梁描述压电悬臂梁的振动特性，在简谐激励的作用下改变输入电压和振动阻尼并与传统双稳态压电发电系统作比较，主要用于取得合适的磁梁间距进行能量优化获取能量，但可能传入的振动与捕获能量装置的振动方向不一致[10-11]。因此存在不规则的振动沿着若干方向传递消散会减少能量转换效率，振动现象未能得到有效改善方案。孙浩等以衰减系数为优化目标采用压电分流的方式所产生的阻尼效应组成谐振电路，电流通过谐振电流的电阻消耗电能进一步减小压电陶瓷片的电压，但提出的振动阻尼优化仅仅考虑了一阶振动模态，未考虑多阶振动模态对实验结果的影响[12]。

针对现有问题，分析智能结构振动现象产生的原因，提升智能结构的系统稳定性减少运行误差是必不可少的。基于动力学方程建立智能悬臂梁结构的数学模型，并确定模型的正确性是进行智能结构振动控制的基础。极点配置控制与其他传统控制相比，能够较为清晰的展示控制逻辑，直观性更强且具有更大的应用环境。其主要思路是利用压电陶瓷片力矩方程结合振型叠加法[13]推导四阶模态的智能悬臂梁结构振动微分方程构建模型，然后运用极点配置算法控制悬臂梁的自由振动，搭建控制系统[14-15]。并通过数值仿真和实验证明，对比阻尼影响下的智能结构控制效果，验证极点配置控制算法能有切实有效的控制自由振动。

1 智能悬臂梁结构的模型推导及验证

1.1 智能悬臂梁结构的模型推导

在悬臂梁与智能结构相结合的条件下，引用力矩平衡和材料力学建立悬臂梁的振动微分方程，基于振型叠加法建立悬臂梁模型。由悬臂梁的力矩平衡方程与材料力学方程得

（M（x，t）+M（x，t）xdx）-M（x，t）+F0（x，t）d2x2

-

（Fs+Fsxdx）dx+m（x，t）dx=0

M（x，t）=EJ（x）2τ（x，t）

x2

（1）

式中 m（x，t）为长度梁的外力矩，N·m;V0（x）为体积的梁质量，g/m3;

S（x）为横截面积，m2;R为悬臂梁长度，m;F0（x，t）为分布在梁外侧的外力，N;

Fs为

横截面剪力，N;M（x，t）为x截面在任意时刻t的弯矩，N·m;E为悬臂梁的弹性模量，

Pa;J（x）为悬臂梁截面中的惯性矩，N·m;

2τ（x，t）x2

为悬臂梁在x截面处在任意时刻t的横向加速度，m/s2.

由于实际的工作中存在阻尼，阻尼阻碍了正常的运动表现，分析悬臂梁振动中的阻尼特性是十分必要的[16-17]，设不同阶次的阻尼为ηi，单位长度的悬臂梁的外力矩m（x，t）=0且作自由振动时对上式做分离式处理，分步求解方程中x和t的相关函数

τ（x，t）=Y（t）Z（x）

d2Ydt2=-a2Y

d4Zdx4=γ4Z，

γ4=a2V0（x）S（x）EJ（x）

（2）

由悬臂梁的初始条件Z（0）=Z′（0）=0转换为函数求解问题，求解2个函数

cosγR与

-1coshγR

的交点问题，如图1所示。

图1中x=γR，由上述MATLAB拟合的函数图像可知，两函数的交点有无穷多个，对此我们仅分析函数的前4个交点即可完成模型的验证，函数的交点分别是

γ1R=1.875，γ2R=4.694，

γ3R=7.855，γ4R=10.996

悬臂梁用函数交点x=γR表示振动系统的固有频率为

ai=γ2i

EJ（x）V0（x）S（x）

，i=1，2，3，…

（3）

代入上式可得前四階固有频率见表1.

结合式（2）可得振型函数Zi（x）为

Zi（x）=chγix-cosγix+φi（shγix-sinγix）

φi=-shγiR-sinγiR

chγiR+cosγiR，i=1，2，3，…

（4）

对于振动系统中的智能悬臂梁结构可用振型叠加法表示系统的连续响应，振型叠加法将多重自由度的函数分解为非有限数量多种响应的代数和，可表示为在任意位置x的振型函数和任意时刻t系统的广义坐标值的乘积相叠加，方程表达式为

τ（x，t）=iZi（x）pi（t），i∈[1，∞）

（5）

不同阶次的振型函数满足正则化，故可取λi（x）=1，式中，pi（t）表示系统的广义坐标值。 整理可得悬臂梁的振动微分方程为

i（t）+2ηiai（t）+a2pi（t）

=KhUi（t）[Z′i（x2）-Z′i（x1）]

（6）

压电材料力矩

Mi（x，t）=KhUi（x，t），Kh=w1ey2Ep（d1+d2）

（7）

式中 K为压电耦合系数;Kh为系统转换常数，w1为悬臂梁的宽度，m;

Ep为压电材料的弹性模量，Pa;d1和d2分别为悬臂梁和压电材料的厚度，

m.

引入连续非时变系统的概念即振动系统的输入为控制电压Ui（t），对pi（t）进行转置处理可得常系统状态表达式为

Lin（t）

=

pi（t）

i（t）

（8）

振动系统的输入电压矩阵为

u（t）=[Ui（t）]

（9）

对应于状态空间模型可列方程式为

in（t）=ALin（t）+Bu（t）+c（t）

c（t）=

0

（t）

=

0

-n2（t）

Lout（t）=XLin（t）

（10）

对于上式X代表传感矩阵可表示为

X=[ 0]

（11）

式中 ={kh[Z′i（x2）-Z′i（x1）}

悬臂梁输入状态方程的向量矩阵可表示为

in（t）=

01

-a2-2ηa

Lin（t）

+

kα

0

Z′i（x2）-Z′i（x1）u（t）

（12）

输出电压方程可转化为

Lout（t）=[kh[Z′i（x2）-Z′i（x1）] 0]Lin（t）

（13）

1.2 基于ANSYS的模型验证

图2是利用ANSYS有限元分析得到的悬臂梁前四阶振型图[18-20]，通过有限元仿真得到的振型图可以较为直观的看出悬臂梁的动态特性，进一步验证模型的正确性。通过表2固有频率理论值与ANSYS求解值的分析结果，可以看到数据比值误差在1%内，则可以说明该模型能够较好的描述悬臂梁动态特性。

2 控制器的设计

2.1 极点配置控制稳定性理论

在线性定常的振动系统中，极点的位置布置不但能够极大程度的影响整体系统的稳定性，而且影响系统稳定性的表现，对应于线性定常的振动系统中常见的表现于超调量、振荡次数、稳定时间等方面。极点配置方法，移动极点使其处于合理的位置对于闭环振动系统实现目标，达到既定的性能要求，极点配置控制律（pole placement control，PPC）具有鲁棒性强、适用广泛、易于考虑条件约束等优点。

2.2 极点配置控制设计

从图2可以看出，阻尼比在0.6～0.8时可获得较好的系统动态，使得系统趋于稳定的速度更加快速。理论上系统阻尼系数应尽可能的接近0.707，但由于供能有限，这个值是达不到的，所以应尽可能的趋近0.707，首先取阻尼值0.65进行验证，实际工作中的阻尼系数的参数值应由PPC控制系统的参数进一步修正，根据不同的阻尼系数的参数值设定智能悬臂梁结构控制电压的极限值。

所设计的控制器可能消除被控对象智能悬臂梁的部分零点，但从实际工作出发，控制器的零点只能消除稳定的被控对象，对于不稳定或不符合预期的零点需尽可能避免抵消。我们设计极点配置控制如下

Fu（k）=Ryr（k+d）-Gy（k）

（14）

式中 y（k）为振动系统的输入信号即位移;u（k）为振动系统的输出信号即电压信号;F，G，R为待定的系统参数矩阵;yr为参考输入;d为纯延时。

智能悬臂梁振动结构中阻尼属于小阻尼体系，可用下式表示实时阻尼比大小

η=12nπlnaiai+1

（15）

式中 ai和ai+1分别对应于智能悬臂梁振动系统中自由振动位移的第i个和第i+1个的位移最大值。

为了求解

F，G，R，可将T设为期望的闭环特征多项式，A和B为期望传递函数的分母因子和分子因子，F，G为待求多项式，进一步求解可将闭环特征多项式方程转化为

AF=T-z-dBG

（16）

式中 A和B的次数分别为n1，n2，

F，G对用的次数可表示为ng=n1-1，nf=n2-1.由于系统的参数不稳定零点与控制器不应该完全抵消，可将A和B矩阵分为2部分，分别是阻尼良好的多项式矩阵和阻尼差的多项式矩阵，保证系统的输出无偏差。

根据系统条件要求，确定观测器多项式

A0，用于对比响应时间，将初始位移數据输入给PPC控制器，确定采集实际输出y（k），并通过计算得到控制电压u（k）.

3 仿真验证和实验验证

3.1 仿真验证

基于极点配置控制算法（PPC）理论，采用MATLAB/SIMULINK编程实现对智能悬臂梁系统进行仿真分析，基于智能悬臂梁系统的方程和极点配置控制理论得到控制系统的参数，见表3.

由前面的模型推导可知，四阶模态中对应状态方程的空间向量次数应为8，相应的控制器的参数阶数应为7.仿真实验中，阻尼η取0.66，纯延时d设为1，对于状态模型可将输入信号y设定为0，添加一个零时刻的位移激励，在该条件下智能悬臂梁作自由振动，仿真结果如图3，4所示。从仿真结果可以得到，在对智能悬臂梁结构施加控制电压后，智能悬臂梁结构的输出位移在5 s内迅速减小，在5 s后输出位移恒定为0，证明PPC控制算法对智能悬臂梁结构的振动控制是有效的。

3.2 实验验证

3.2.1 实验原理及装置

实验装置如图5所示，实验器材有：压电陶瓷片、HPV功率放大器、电压转换器、LK-G30激光位移传感器、MCC_USB 1808X数据采集器和计算机LABVIEW软件组成的实验平台。

实验原理如下：压电陶瓷片紧附于悬臂梁上并随之运动，给悬臂梁施加一个初始位移激励，由于压电陶瓷片的材料特性，在有传感作用的同时又兼顾驱动作用，进而压电陶瓷片内部产生与运动方向相反的电荷抑制悬臂梁的振动。利用数据采集器采集运动过程中的电压波动变化，位移的变化由激光位移传感器采集，LABVIEW作为实时编程控制工具将采集到的电压和位移信号输入，由极点配置控制程序对悬臂梁的振动进行抑制。

3.2.2 实验结果

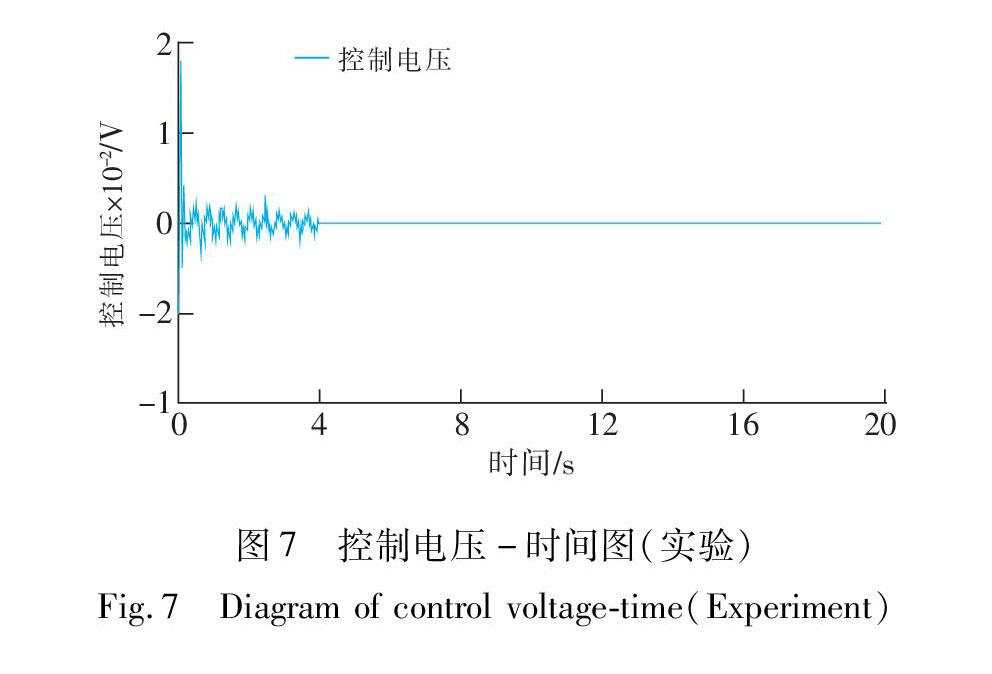
实验过程中，需要尽可能的避免误差，减少外部的不稳定因素。实验前需对激光位移传感器进行清零和输入电压信号的清零，并需要多次反复实验来选择合适的实验数据，结果如图6，7所示。

从图6，图7可以看出，在初始振动位移为6 mm时，智能悬臂梁结构在控制电压的作用下输出位移在6 s内迅速衰减，从6 mm迅速衰减至2 mm，短时间内输出位移减小了66%;与此同时智能悬臂梁结构的控制电压在控制初始阶段有明显激增，控制电压在6 s内逐渐减小趋于稳定达到良好的控制效果。由于实际工作不可能存在完全真空的理论环境，实验过程中智能悬臂梁结构的振动还有受到空气阻力、噪声等外界因素的干扰，故仿真结果与实验结果存在一定程度的误差。智能悬臂梁结构的振动情况得到明显改善，达到预期实验效果，证明PPC控制算法对智能悬臂梁结构的振动控制是有效的。

4 结 论

1）压电材料与悬臂梁结构组成的智能悬臂梁结构中的压电材料对实验结果有着重大影响，将输出位移减小了66%，压电材料能够改善智能悬臂梁结构的振动现象。

2）在初始位移信号为6 mm时，数值仿真和实验验证结果在5 s内输出位移迅速衰减，结果的一致性证明了PPC控制算法的可靠性，可以进行自由振动下的智能悬臂梁结构的主动振动控制。

参考文献（References）：

[1]

杨正岩，张佳奇，高东岳，等.航空航天智能材料与智能结构研究进展[J].航空制造技术，2017，60（17）：36-48.YANG Zheng-yan，ZHANG Jia-qi，GAO Dong-yue，et al.Advance of aerospace smart material and structure[J].Aeronautical Manufacturing Technology，2017，60（17）：36-48.

[2]孟光，周徐斌.卫星微振动及控制技术进展[J].航空學报，2015，36（8）：2609-2619.MENG Guang，ZHOU Xu-bin.Progress review of satellite micro-vibration and control[J].Acta Aeronautica et Astronautica Sinica，2015，36（8）：2609-2619.

[3]付云.柔性航天器边界振动控制研究[D].广州：华南理工大学，2019.

FU Yun.Research on boundary vibration control of flexible spacecraft[D].Guangzhou：South China University of Technology，2019.

[4]耿胜男，冯辉，王星来，等.航天器智能结构与先进传感技术[J].遥测遥控，2017，38（5）：44-48.GENG Sheng-nan，FENG Hui，WANG Xing-lai，et al.Smart structures and advanced sensing technologies in space vehicles[J].Journal of Telemetry，2017，38（5）：44-48.

[5]AHMAD S F，EMAD A.Thermoelastic vibration and maneuver control of smart satellites[J].

Aircraft Engineering & Aerospace Technology，

2017，89（3）：477-490.

[6]吴曼乔，朱继宏，杨开科，等.面向压电智能结构精确变形的协同优化设计方法[J].力学学报，2017，49（2）：380-389.WU Man-qiao，ZHU Ji-hong，YANG Kai-ke，et al.Integrated layout and topology optimization design of piezoelectric smart structure in accurate shape control[J].Chinese Journal of Theoretical and Applied Mechanics，2017，49（2）：380-389.

[7]张新亚，雷晓燕，罗锟.TMD在简支箱梁多阶模态振动控制中的应用[J].噪声与振动控制，2019，39（5）：78-83.ZHANG Xin-ya，LEI Xiao-yan，LUO Kun.Application of TMD in multi-order modal vibration control of a simply supported box girder[J].Noise and Vibration Control，2019，39（5）：78-83.

[8]刘华中.基于张量的大数据高效计算及多模态分析方法研究[D].武汉：华中科技大学，2018.LIU Hua-zhong.A tensor based big data efficient computation and multimodal analysis approach[D].Wuhan：Huazhong University of Science and Technology，2018.

[9]陈文英，褚福磊，阎绍泽.基于自适应遗传算法分步优化设计智能桁架结构自抗扰振动控制器[J].机械工程学报，2010，46（7）：74-81.

CHEN Wen-ying，CHU Fu-lei，YAN Shao-ze.Stepwise optimal design of active disturbances rejection vibration controller for intelligent truss structure based on adaptive gene tic algorithm[J].Journal of Mechanical Engineering，2010，46（7）：74-81.

[10]杨炯炯.一种双稳态压电悬臂梁发电装置的动力学特性研究[D].西安：西安理工大学，2019.YANG Jiong-jiong.Dynamic characteristics of a bistable piezoelectric cantilever generator[D].Xian：Xian University of Technology，2019.

[11]高毓璣.非线性双稳压电悬臂梁振动响应及能量采集研究[D].天津：天津大学，2017.GAO Yu-ji.Studies on nonlinear bistable piezoelectric cantilever vibration energy harvesting[D].Tianjin：Tianjin University，2017.

[12]孙浩，杨智春，于哲峰.基于极点配置参数优化的压电分流阻尼抑振研究[J].西北工业大学学报，2006，24（1）：106-110.SUN Hao，YANG Zhi-chun，YU Zhe-feng.Vibration control with optimized piezoelectric shunt damping system using pole placement[J].Journal of Northwestern Polytechnical University，2006，24（1）：106-110.

[13]CORRADO G，UBALDO C，EMILIANO C，et al.Fast high fidelity CFD/CSM fluid structure interaction using RBF mesh morphing and modal superposition method[J].Aircraft Engineering & Aerospace Technology，2019，91（6）：893-904.

[14]周鹏飞，崔玉国，惠相君，等.压电微动平台的极点配置PID控制[J].压电与声光，2019，41（6）：830-834.ZHOU Peng-fei，CUI Yu-guo，HUI Xiang-jun，et al.Pole configuration PID control of a piezoelectric micro-positioning stage[J].Piezoelectrics & Acoustooptics，2019，41（6）：830-834.

[15]DING Y S，XIAO X.Parameter tuning methods based on pole placement for PI controllers of flexible loads driven by PMSM[J].Proceedings of the Chinese Society for Electrical Engineering，2017，37（4）：1225-1239.

[16]謝伟平，郭漫，孙亮明.线弹性范围内钢悬臂梁的阻尼特性试验研究[J].振动工程学报，2016，29（6）：1011-1019.XIE Wei-ping，GUO Man，SUN Liang-ming.Experi-mental study on damping characteristics of the steel cantilever beam in the linear elastic range[J].Journal of Vibration Engineering，2016，29（6）：1011-1019.

[17]吴晴晴.粘弹复合结构动态力学参数理论及应用研究[D].西安：西北工业大学，2018.WU Qing-qing.Theoretical and application study of dynamic mechanical properties of viscoelastic composite structures[D].Xian：Northwestern Polytechnical University，2018.

[18]王飞朝.基于有限元模型的结构动力修改程序开发[J].西安科技大学学报，2007，27（3）：443-447.WANG Fei-chao.Program development of dynamic modification based on FEM model[J].Journal of Xian University of Science and Technology，2007，27（3）：443-447.

[19]李海峰，吴冀川，刘建波，等.有限元网格剖分与网格质量判定指标[J].中国机械工程，2012，23（3）：368-377.LI Hai-feng，WU Ji-chuan，LIU Jian-bo，et al.Finite element mesh generation and decision criteria of mesh quality[J].China Mechanical Engineering，2012，23（3）：368-377.

[20]于水情，唐映德.网络化切换系统中状态观测器的设计[J].西安科技大学学报，2007，27（1）：130-133，142.YU Shui-qing，TANG Ying-de.Design of state observer of networked switching systems[J].Journal of Xian University of Science and Technology，2007，27（1）：130-133，142.