巷道底板砂岩三轴压缩蠕变试验与分数阶模型

刘朝科 任建喜

摘 要：為解决传统非线性蠕变模型不能反映模型参数的损伤时效问题，采用西安科技大学和长春朝阳试验仪器有限公司联合研制的高温三轴流变试验机对煤矿巷道底板软砂岩试样进行了三轴压缩蠕变实验，得到软砂岩在三轴压缩下的蠕变变形规律和破坏特征。基于分数阶微分理论，考虑模型参数的损伤时效，通过引入损伤变量，推导得到了一维四元件非定常分数阶蠕变损伤模型和三维模型，并对模型参数进行了敏感性分析，参数β变化可描述砂岩的不同阶段的变形特点，参数α可描述砂岩随时间的损伤规律。根据蠕变试验数据，采用粒子群算法和最小二乘法对分数阶模型参数进行了辨识，将试验曲线、分数阶模型与Burgers模型曲线进行了对比分析，验证了模型的正确性和优越性。研究结果表明，随着底板软砂岩的偏应力水平增大，瞬时应变、蠕变变形、蠕变速率及损伤程度也随着增大，巷道底板的偏应力水平是控制软砂岩变形的关键因素;建立的非定常分数阶蠕变损伤模型能够准确描述巷道底板软砂岩的衰减蠕变、稳态蠕变和加速蠕变的变形特征，尤其描述软砂岩加速段变形规律具有一定的优势，与传统的Burgers模型相比，且具有参数少，并能反映不同阶段模型参数损伤规律的特点。研究结果对相关工程具有一定的应用价值。 关键词：巷道底板软砂岩;三轴压缩蠕变;蠕变损伤;分数阶微分模型中图分类号：

TU 45

文献标志码：A

文章编号：1672-9315（2020）06-01003-07

DOI：10.13800/j.cnki.xakjdxxb.2020.0610开放科学（资源服务）标识码（OSID）：

Triaxial compression creep test of roadway floor sandstone

and fractional order model

LIU Chao-ke，REN Jian-xi

（College of Civil and Architectural  Engineering，Xian University of Science and Technology，Xian 710054，China）

Abstract：In order to solve the problem that the nonlinear creep model cannot reflect the damage law of each parameter with time，triaxial creep experiments were carried out on soft sandstone samples in coal mine roadway floor by the high temperature triaxial rheological testing machine，developed by the research group of Xian university of science and technology and Changchun Chaoyang Test Instrument Company，and the creep deformation and failure characteristics of soft sandstone under triaxial compression are obtained.Considering the damage timeliness of the model parameters，the unsteady fractional-order creep damage model of four elements is established.The sensitivity analysis of the model

parameters is carried out.The variation of parameter β can describe the deformation characteristics of sandstone at different stages，and the parameter α  the damage law of sandstone characteristics with time.Based on the experimental results，the parameters of the fractional order model were identified by particle swarm optimization.The results show that with the increase of deviatoric stress，the instantaneous strain，creep deformation，creep change rate and damage degree also increase，and the deviating stress level of roadway floor is the key factor of floor heave control.The fractional-order differential creep damage model established can accurately describe the creep deformation characteristics of soft sandstone in roadway floor，in particular，it can describe the deformation in the acceleration phase，it has the characteristics of few parameters and can reflect the damage law of model parameters in different stages.The results of the study are valuable in applications into related engineering.

Key words：soft sandstone of roadway floor;triaxial compression creep;creep damage;fractional order differential model

0 引 言

近年来，随着煤炭开采深度的增加，软岩相关的工程问题逐渐增多，其中软岩的流变导致巷道稳定性问题日益凸显[1-3]。国内外学者对于巷道流变特性进行了广泛的研究，并取得显著成果[4-7]。岩石的蠕变特性是工程岩体重要力学特性之一[8]。建立能全面反映蠕变特性的岩石非线性蠕变模型是当前岩石蠕变特性研究的重要课题。室内试验表明，软砂岩蠕变变形表现为减速蠕变、等速蠕变以及加速蠕变这3个过程。为了描述软砂岩的蠕变变形特点，目前国内外学者通常采用元件组合模型。而传统的Burger模型和Nishihara模型仅能描述岩石的减速蠕变和等速蠕变，不能描述加速蠕变阶段，为了解决这一问题，国内外学者通过改进线性元件为非线性元件或者在已有的模型中引入损伤变量。赵延林将传统Burger模型和非线性塑性元件串联，建立了一个新的蠕变损伤模型，并验证该模型模的合理性[9]。流变损伤模型方面，CHAN等基于细观力学研究了盐岩流变变形与损伤演化之间的关系[10-15]。WANG在针对盐岩流变损伤特性研究的基础上，建立了基于损伤理论的流变本构模型[16]。殷德顺等将分数阶微分理论应用于岩石变形元件，提出了软体元件，该元件在描述岩石加速蠕变阶段具有一定的优势[17]。陈亮等则以分数阶微积分为基础构建了一种新的岩石四元件蠕变模型[18]。陈军浩等将分数阶微积分理论运用到了人工冻土蠕变模型中[19]。以上蠕变模型研究虽取得丰硕的成果，但模型不能客观反映各参数随时间的损伤规律，文中基于分数阶微分理论建立了四元件非线性蠕变模型，描述巷道底板软砂岩蠕变变形特点，并根据巷道底板砂岩的蠕变试验结果对模型参数进行了辨识，并能反映模型参数不同阶段的损伤规律。

1 巷道底板软砂岩三轴压缩蠕变试验

1.1 岩样制备

软砂岩采自于黄陵矿区某矿一盘区运输大巷底板，样本易风化、在水中易分解，岩样在现场采集好后立即封存，在运输过程中尽可能做到轻拿轻放，避免较大的震动破坏软砂岩的结构和完整性。岩块在室内实验室经过钻取、切割和打磨三道工序后，按国际标准尺寸加工成50×100 mm的标准试件，然后用非金属超声检测分析仪剔除波速和波形相差较大的试件，所有试件在试验前在水中浸泡不小于48 h，试件处于饱和状态，如图1所示。文中试件试验均在饱和状态下进行。

1.2 试验设备与加载方案

采用高温三轴蠕变试验机完成软砂岩的蠕变试验。在实验前对试件进行饱水，为加载准备，饱水后进行围压为5 MPa下的三轴压缩蠕变试验。采用分级加载方式，第1级荷载为σ1=7 MPa，第2级σ1=9 MPa，第3级σ1=11 MPa，第4级σ1=13 MPa.采用应力控制加载，加载速率为0.001 5 MPa/s，每级荷载加载时间不小于24 h.

1.3 试验结果与分析

图2为围压5 MPa下巷道底板软砂岩压缩蠕变曲线。试样在每一级应力加载的初期都产生较大的瞬时变形，偏应力为2 MPa作用下产生的瞬时应变量达到680 με，在偏应力4，6，8 MPa下产生的瞬时应变增大量依次为320，380和680 με，表明随着偏应力水平的增大，瞬时应变逐渐增大。蠕变变形量也有增大趋势，在2，4和6 MPa下的蠕变量，依次增大47，70，92 με.在2，4和6 MPa时由于偏应力较小都经历了衰减蠕变，经过约8 h后蠕变速率趋近于零。当偏应力达到8 MPa时，经过约8个小时的等速蠕变之后进入了加速蠕变阶段，应变开始急剧增大，最后砂岩内部结构发生破坏。以上分析表明，随着偏应力水平的增大，瞬时应变、蠕变变形与蠕变速率也随着增大。巷道底板的偏应力水平是影响巷道底板变形规律和稳定性的关键因素。

图3为试件破坏前后照片，从图中可知试件破坏后为单一裂纹。裂纹从试件顶部边缘部位沿75°向下延伸至试件底部，属于弱面剪切破坏，也是延性破坏。

2 基于分数阶的非线性蠕变本构模型

元件模型虽然能较好地模拟砂岩的流变，但要准确模拟流变的每个阶段的变形，必然要增加元件的数目，从而使未知参数增多。因此，文中基于分数阶微分理论，建立了四元件非线性蠕变损伤模型来描述砂岩的蠕变变形特点。

2.1 基于分数阶微分的元件

分数阶微积分是一种研究任意阶次的微分、积分算子特性及其应用的数学方法。目前应用最广泛的3种定义：Riemann-Liouville定义、Caputo定义以及 Grunwald-Letnikov定义。文中采用的是Riemann-Liouville算子理論[20-22]。

采用分数阶微分形式表述的应力-应变关系式为

σ（t）=ηdβε（t）dtβ

（1）

式中 σ为应力，MPa;ε为应变，‰;β为分数阶阶数，无量纲;t为时间，h;η为类粘滞系数，

MPa·hβ。

蠕变过程中应力保持恒定，对公式（1）进行Laplace变换去掉阶次，得到结果在进行Laplace逆变换后，可得到应变和时间之间的表达式，考虑到应力

σ

为常数，对其结果进行积分后可得

ε（t）=ση tβΓ（1+β）

（2）

式中 Γ（1+β）=∫t0tβt-tdt，为Gamma函数。

当β=0，式（2）表现为弹性体，即胡克体，可模拟理想固体;当β=1，式（2）表现为黏性，即牛顿体，可模拟理想流体;当0<β<1，式（2）表现性质介于固体和流体之间，当β>1，可描述加速流变物质状态，因此将0<β<1和β>1时，称为软体元件。

2.2 分数阶非线性蠕变模型

岩石蠕变试验在加载瞬间，岩石会产生较小

的弹性变形，这一阶段变形可用弹性体描述其变形。

εe=σE，β=0

（3）

式中 E为弹性模量，MPa.经过暂短的弹性变形后，岩石进入了黏弹性变形，这一阶段的变形特征可用

0<β<1的软体元件表达。

εve=ση1

tβ1Γ（1+β1）

，0<β<1

（4）

式中 η为黏滞系数，MPa，hβ.黏弹性变形之后，岩石进入了黏塑性变形阶段，这一阶段加速流变可用β>1的软体元件描述。

εvp=ση2

（t-t*）β2Γ（1+β2）

，β>1

（5）

式中 t*为加速蠕变起始时刻，h.

根据流变的三阶段变形特征，將以上3个元件进行串联叠加，即可得到巷道底板砂岩的非线性蠕变模型，如图4所示。

根据元件模型的状态方程，并进行Laplace变换和逆变换后，得到非线性蠕变本构方程如下。

ε=σE+ση1

tβ1Γ（1+β1）

，σ≤σs

ε=σE+ση1

tβ1Γ（1+β1）

+

σ-σsη2

（t-t*）β2Γ（1+β2）

，

σ>σs

（6）

软砂岩在蠕变过程中，砂岩的力学性质发生变化，尤其是加速蠕变阶段，软砂岩的损伤较为明显，砂岩的弹性模量、粘性系数等将不再是常数，也会随着时间的增长发生劣化，因此可引入损伤变量D，考虑软砂岩的损伤问题，D∈[0，1]之间的数值，D=0表示砂岩没有损伤，D=1，表示砂岩完全破坏。煤矿巷道底板软砂岩蠕变试验得到弹性模量的变化规律，损伤变量变化规律[23]，可简化为

D=1-eαt

（7）

根据公式（1）中可得

ξ（t）=e-αtξ

（8）

将式（8）代入到公式（1），根据变阶分数阶微分算子对式（1）两侧进行积分，考虑到

σ

为常数，可以得到变阶分数阶元件的表达式

ε（t）=σ0ξtβE1，1+β（αt）

（9）

式中 Eα，β（z）=∞k=0

zkΓ（α+β）

为Mittag-Leffle函数。

根据公式（6）考虑蠕变损伤后，可得到非线性蠕变损伤本构方程如下

ε=σEeαt

+ση1tβ1E1，1+β1（αt），σ≤σs

ε=σEeαt

+ση1tβ1E1，1+β1（αt）

+

σ-σsη2（t-t*）β2E1，1+β2（αt）

，σ≤σs

（10）

根据广义胡克定律，弹性体的三维本构关系为

εeij=12GSij+σm3Kδij

（11）

式中 εeij为胡克体的应变张量;Sij为偏应力张量;σm为球应力张量;δij为Krobecker函数。G和K分别为剪切模量和体积模量。

对于黏塑性体可表示为

εpij=

〈F〉η2e-αt

gσij

（12）

式中 F为屈服函数;g为岩石的塑性函数;σij为偏应力张量。

蠕变变形应包括黏弹性和黏塑性，根据屈服函数和等围压条件，可得其三维蠕变方程。

当

σ≤σs

时，可表示为

ε=σ1+2σ33Kδij+

σ1-σ33G

+

σ1-σ3η1tβ1E1，1+β1（αt）

（13）

当σ>σs时，可表示为

ε=σ1+2σ33Kδij+

σ1-σ33G

+

σ1-σ3η1tβ1E1，1+β1（αt）+

σ1-σ3-σsη2（t-t*）β2E1，1+β2（αt）

（14）

3 参数敏感性分析

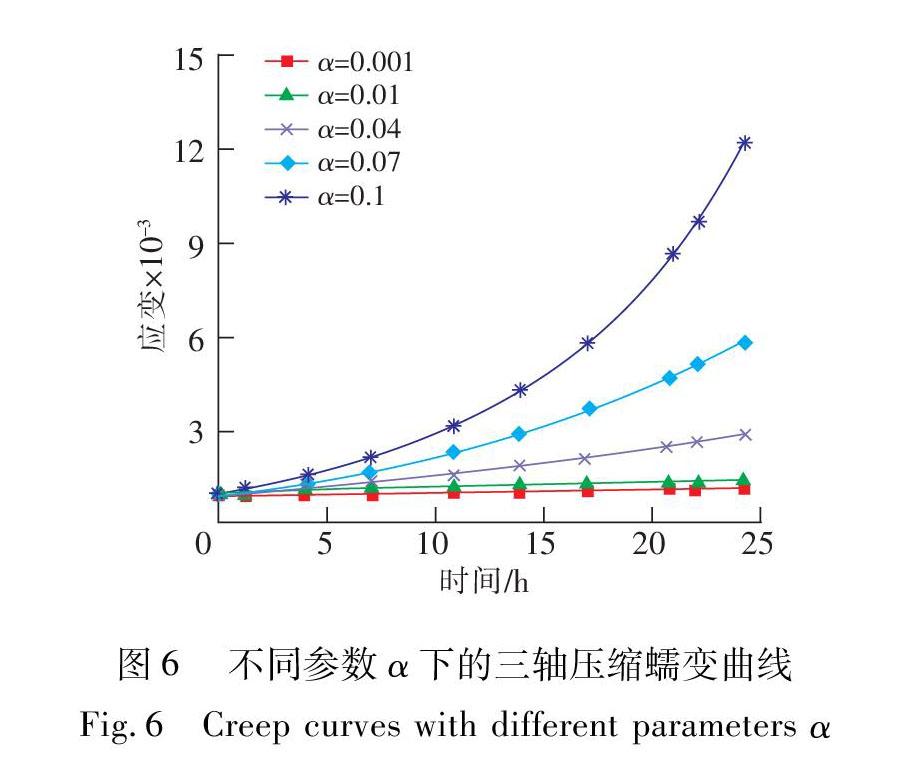
为了研究蠕变本构方程中的分数阶阶数β的影响，公式（6）中其余参数不变，仅变化参数β，使β在（0，2）的区间变化，可得到不同阶数下的蠕变曲线如图5所示。图 6为所有参数不变仅变化参数α，研究参数α的影响。

由图5可知，随着阶数β的增大，蠕变速率呈现增大趋势，当β<1时，呈现为黏弹性，可描述砂岩在低应力状态下的稳态蠕变过程;当1<β<2时，

呈现黏塑性，可描述砂岩的加速蠕变阶段变形规律。

由图6可知，参数α越大，模型参数随着时间变化衰减速率越快，砂岩的损伤速率也越大，参数α的大小能较好的反映不同阶段的损伤演化规律。

4 模型辨识

粒子群算法由模拟鸟群觅食的优化方法。首先随机赋予各个参数初始值，即随机生成N组M维粒子组成的粒子群，然后通过迭代法方法找到最优解。每个粒子即参数在解空间同时向两点接近，一是能够使全局最优解，其次获得个体最优解。

采用粒子群算法和最小二乘法联合反演的方法对分级加载蠕变模型参数进行辨识[23-24]，实施步骤为

1）利用改进粒子群算法对分级加载蠕变参数先进行参数辨识。

2）将粒子群算法的辨识结果作为初始值再进行最小二乘法反演。

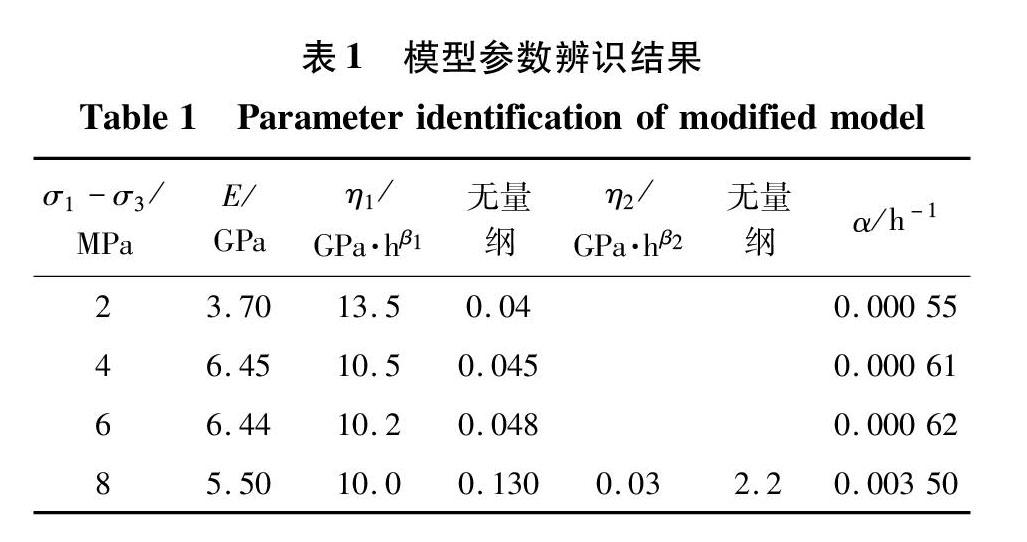
分数阶模型各参数拟合结果见表1.分数阶模型拟合曲线如图7所示，由图可知，考虑损伤的分数阶微分模型与试验曲线吻合度较高，模型能够很好描述巷道底板软砂岩的衰减、稳态和加速三阶段的变形特点，尤其是描述加速阶段的变形，分数阶微分的数学特性相对于Burgers模型，描述砂岩加速蠕变具有明显的优势。通过表1可知，分数阶微分模型相对于其他模型具有参数少的特点。随着偏应力增大，参数β1逐渐变大，表明巷道底板砂岩的蠕变速率逐渐增大;随着偏应力增大，参数α逐渐增大，表明损伤变量逐渐增大，即损伤逐渐加剧。当偏应力较小时各阶段的损伤差别较小，当偏应力达到其长期强度时参数变化较大，表明此阶段损伤相对较大，因此控制砂岩的偏应力水平是控制砂岩蠕变变形和损伤程度的关键因素。

5 结 论

1）砂岩三轴压缩蠕变试验表明，随着偏应力水平的增大，瞬时应变、蠕变变形与蠕变速率也随之增大。参数α逐渐增大，表明损伤变量逐渐增大，即损伤逐渐加剧。当偏应力较小时各阶段的损伤差别较小，当偏应力达到其长期强度时參数变化较大，表明此阶段损伤相对较大，因此控制砂岩的偏应力水平是控制砂岩蠕变变形和损伤程度的关键因素。

2）基于分数阶Abel 黏壶元件，引入损伤变量建立了非定常分数阶微分蠕变损伤模型，模型能够描述软砂岩不同阶段蠕变变形规律。尤其描述软砂岩加速段变形规律与传统的Burgers模型相比，具有一定的优势，且具有参数少，并能反映不同阶段模型参数损伤规律的特点。

3）采用粒子群算法和最小二乘法对非定常分数阶蠕变模型进行了验证，结果表明，模型能很好描述软砂岩的蠕变变形特点，尤其是描述砂岩加速阶段变形特点具有较大的优势。研究结果对相关工程具有一定的应用价值。

参考文献（References）：

[1]

丁国峰，王苏健，谢文兵，等.加固顶板和两帮控制回采巷道底臌研究[J].西安科技大学学报，2014，34（4）：384-389.DING Guo-feng，WANG Su-jian，XIE Wen-bing，et al.Mechanism of reinforcing roof and sides for floor heave control of roadway[J].Journal of Xian University of Science and Technology，2014，34（4）：384-389.

[2]张宁，张幼振，陈盼.煤矿巷道底鼓治理机群施工建模及优化配置[J].西安科技大学学报，2019，39（1）：96-102.ZHANG Ning，ZHANG You-zhen，CHEN Pan.Construction modeling and optimal allocation of roadway floor heave control group in coal mine [J].Journal of Xian University of Science and Technology，2019，39（1）：96-102.

[3]文志杰，卢建宇.软岩回采巷道底臌破坏机制与支护技术[J].煤炭学报，2019，44（7）：1991-1999.WEN Zhi-jie，LU Jian-yu.Failure mechanism of floor heave and supporting technology of soft rock roadway[J].Journal of China Coal Society，2019，44（7）：1991-1999.

[4]

贺永年，何亚男.茂名矿区巷道底臌实测与分析[J].岩土工程学报，1994，16（4）：40-46.HE Yong-nian，HE Ya-nan.Analysis of the measured results on the floor heave in Maoming mine[J].Chinese Journal of Geotechnical Engineering，1994，16（4）：40-46.

[5]李伟，杨仁树.深部岩石巷道底鼓流变分析[J].煤炭技术，2013，32（5）：53-55.LI Wei，YANG Ren-shu.Rheological analysis of floor heave in deep rock roadway[J].Coal Technology，2013，32（5）：53-55.

[6]

史宏财.高温预损伤下煤岩蠕变声发射及分形特征[J].煤田地质与勘探，2020，48（2）：187-194.

SHI Hong-cai.

Creep acoustic emission and fractal characteristics of coal rock under high temperature pre-damage[J].

Coal Geology & Exploration，2020，48（2）：187-194.

[7]李斌，王大国.常规三轴压缩条件下的负乘方型岩石强度准则[J].煤田地质与勘探，2020，48（2）：151-160.

LI Bin，WANG Da-guo.Negative power rock strength criterion under conventional triaxial compression

[J].Coal Geology & Exploration，2020，48（2）：152-160.

[8]孙钧.岩石流变力学及其工程应用研究的若干进展[J].岩石力学与工程学报，2007，26（6）：1081-1106.SUN Jun.Rock rheologaical mechanics and its advance in engineering application[J].Chinese Journal of Rock Mechanics and Engineening，2007，26（6）：1081-1106.

[9]赵延林，唐劲舟，付成成，等.巖石黏弹塑性应变分离的流变试验与蠕变损伤模型[J].岩石力学与工程学报，2016，35（7）：1297-1308.ZHAO Yan-lin，TANG Jin-zhou，FU Cheng-cheng，et al.Rheological test of separation between viscoelastic-plastic strains and creep damage model[J].Chinese Journal of Rock Mechanics and Engineening，2016，35（7）：1297-1308.

[10]CHAN K S，BODNER S R，FOSSUM A F，et al.A damage mechanics treatment of creep failure in rock salt[J].International Journal of Damage Mechanics，1997，6（2）：121-152.

[11]TANG S，GREENE M S，LIU W K.Two-scale mechanism-based theory of nonlinear viscoelasticity[J].Journal of the Mechanics and Physics of Solids，2012，60（2）：199-226.

[12]CHEN W，ZHANG J J，ZHANG J Y.A variable-order time-fractional derivative model for chloride ions sub-diffusion in concrete structures[J].Fractional Calculus and Applied Analysis，2013，16（1）：76-92.

[13]FU Z J，CHEN W，YANG H T.Boundary particle method for Laplace transformed time fractional diffusion equations[J].Journal of Computational Physics，2013，23（5）：52-66.

[14]WANG G J.A new constitutive creep-damage model for salt rock and its characteristics[J].International Journal of  Rock Mechanics and Mining Sciences，2004，41（1）：61-67.

[15]TANG S，GREENE M S，LIU W K.Two-scale mechanism-based theory of nonlinear viscoelasticity[J].Journal of the Mechanics and Physics of Solids，2012，60（2）：199-226.

[16]WANG G J.A new constitutive creep-damage model for salt rock and its characteristics[J].International Journal of Rock Mechanics and Mining Sciences，2004，41（1）：61-67.

[17]殷德顺，任俊娟，和成亮，等.一种新的岩土流变模型元件[J].岩石力学与工程学报，2007，26（9）：1899-1903.YIN De-shun，REN Jun-juan，HE Cheng-liang，et al.A new rheological model element for geomaterialst[J].Chinese Journal of Rock Mechanics and Engineening，2007，26（7）：1297-1308.

[18]陈亮，陈寿根，张恒，等.基于分数阶微积分的非线性黏弹塑性蠕变模型[J].四川大学学报（工程科学版），2013，45（3）：7-11.CHEN Liang，CHEN Shou-gen，ZHANG Heng，et al.A nonlinear viscoelasto-plastic creep model based on fractional Calculus[J].Journal of Sichuan University（Engineering Science Edition），2013，45（3）：7-11.

[19]陈军浩，姚兆明，徐颖，等.人工冻土蠕变特性

粒子群分数阶导数模型[J].煤炭学报，2013，38（10）：1763-1768.CHEN Jun-hao，YAO Zhao-ming，XU Ying，et al.Particle swarm fractional order derivative model of artificial frozen soil creep properties[J].Journal of China Coal Society，2013，38（10）：1763-1768.

[20]

ADOLFSSON K，ENELUND M，OLSSON P.On the fractional order model of viscoelasticity[J].Mech Time-Dependent Mater，2005，59（9）：15-34.

[21]

WELCH S W J，RORRER R A L，DUREN R G.Application of time-based fractional calculus methods to viscoelastic creep and stress relaxation of materials[J].Mech Time-Dependent Mater，1999，51（3）：279-303.

[22]XU M Y，TAN W C.Intermediate processes and critical phenomena：theory，method and progress of fractional operators and their applications to modern mechanics[J].Sci China Ser G-Phys Mech Astron，2006，49（3）：257-272.

[23]

崔峰，马成卫.基于蠕变全过程的广义凯尔文体力学损伤模型改进与验证[J].西安科技大学学报，2020，40（1）：58-63.CUI Feng，MA Cheng-wei.Improvement and verification of generalized Kelvin damage model based on the whole creep process[J].Journal of Xian University of Science and Technology，2020，40（1）：58-63.

[24]屈丽娜.基于煤体三轴蠕变试验的非线性伯格斯模型[J].西安科技大学学报，2019，39（6）：985-991.QU Li-na，A nonlinear burgers model based on triaxial creep test of coal[J].Journal of Xian University of Science and Technology，2019，39（6）：985-991.