磷石膏-氨-水固碳反应体系氨浓度对石膏颗粒溶解速率的影响

2020-08-19吴林李季朱家骅宫源葛敬

化工学报 2020年8期

吴林，李季，朱家骅，宫源，葛敬

（四川大学化学工程学院，四川成都610065）

引言

人类工业活动排放CO2带来的环境问题日益严峻，通过碳减排延缓气候改变是当代人类的共同责任[1]。但CO2捕集和封存技术(CCS)面临经济和技术障碍[2]，主要原因是能耗大[3]、经济效益低及尾气二次污染[4]，突破这三大瓶颈是开发大规模工业化固碳技术的关键。利用工业固废石膏(主要成分CaSO4·2H2O)固碳并转化为碳酸钙与硫酸盐，是一条废物资源化与循环利用的碳减排技术路线[4]。全球每年产生工业固废石膏数亿吨，仅磷石膏(磷化工固废)即可达280 Mt[5]，大量堆砌污染环境，若将其用于固碳则可一举两得。磷石膏-氨-水固碳体系直接矿化烟气CO2的核心技术是三相流化矿化反应系统(图1)[6]，包括液相氨浓度为mol·L-1量级的高浓度矿化结晶循环回路和液相氨浓度为μmol·L-1～mmol·L-1量级的低浓度尾气吸收净化(NH3＜10 ml·m-3)循环回路。粒径小于1 mm 的磷石膏颗粒从含微量氨的尾气吸收循环回路加入系统开始、到输送至矿化结晶循环回路与烟气和高浓度氨溶液进行复分解反应，磷石膏颗粒一直在溶解直至完全转化为碳酸钙结晶，反应转化率实际也就是磷石膏颗粒溶解率，可见溶解过程是该矿化反应系统的控制性步骤。

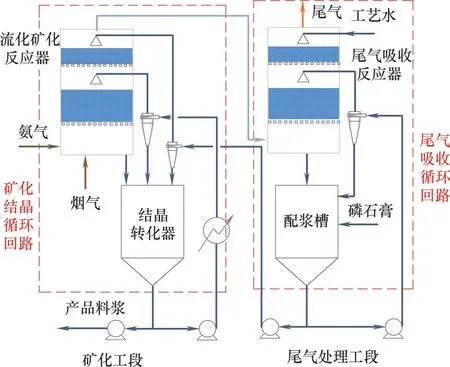
图1 磷石膏-氨-水固碳体系三相流化矿化反应系统[6]Fig.1 The three-phase fluidized mineralization reaction system in the phosphogypsum-ammonia-water system for carbon sequestration

磷石膏-氨-水固碳体系主反应为：

氨作为一种碱性促进剂一方面可高效吸收CO2形成富碳酸根溶液，另一方面在液相形成碱性的铵离子与磷石膏溶解生成的硫酸根反应，促使复分解反应向右进行[7]。石膏的溶解速率显著影响钙碳转移效率[8]，是矿化反应的控速步骤[9-10]。但该体系中石膏溶解速率的改变尚未引起关注，而本课题组前期开展的烟气直接矿化磷石膏的中试研究发现石膏在氨溶液中的溶解速率显著低于在纯水中[11]。这一现象在该工艺放大设计时不容忽视，特别是工艺过程中磷石膏颗粒同时在氨浓度相差3个多数量级的矿化结晶循环回路和尾气吸收循环回路中溶解，溶解速率是计算磷石膏浆料在两个回路中停留时间的理论依据。尽管对石膏溶解已有广泛的研究，但长期认为石膏(CaSO4·2H2O)溶解受颗粒表面液膜内扩散传质控制[12-13]，通过搅拌等消除扩散影响的措施可使其处于表面反应控制[14]。最近通过纳尺度原位观察石膏在纯水中的溶解[15]，发现石膏颗粒具有的多个晶面边缘和交界点提供的台阶和扭结点会加快溶解，而微观尺度上石膏表面溶解反应速率与其晶面微结构密切相关。

上述纯水中石膏溶解微观机制提示，氨水溶液中石膏颗粒表面溶解微结构会受氨介质作用而改变，宏观溶解速率应与溶液的氨浓度相关，尽管微观结构尚难于表征，但宏观效应可以通过不同浓度氨水溶液中石膏颗粒溶解实验数据进行关联。为此，本文针对氨浓度对石膏颗粒群溶解特性的影响规律，实验测定了具有粒度分布的石膏颗粒群在不同氨浓度下的溶解数据。采用种群平衡[16-17]与物料衡算相结合的方法，结合实验数据关联拟合溶解动力学参数，构建氨浓度影响下石膏颗粒群溶解速率模型，以期为磷石膏矿化CO2反应体系的放大设计提供理论依据。

1 机理与模型

1.1 氨浓度影响石膏溶解机理

氨水溶液中石膏颗粒表面溶解微结构会受氨介质作用而改变。如图2(a)所示，在CaSO4·2H2O 的晶体结构中，两层SO2-4被Ca2+从上下两面连接形成坚固的Ca-O 双层结构。Ca-O 双层由中间的H2O 层通过氢键连接。这种氢键作用较弱，容易断裂，因此CaSO4·2H2O 在(010)方向上呈现出逐层溶解的特性[18]。体系中99%的氨以NH3的形式存在，NH3中N的极性强，使得H 几乎以质子态的形式存在，提供了形成氢键的多个位点[19]。添加剂在矿石表面形成氢键抑制溶解的报道较多[20-22]，据此推测NH3中的H会在CaSO4·2H2O 表面与相邻Ca-O 双层中的O 原子形成N—H···O 氢键，如图2(b)所示，增大了相邻Ca-O 双层间的稳定性，同时新氢键使得NH3附着在CaSO4·2H2O 晶体的表面，增大了层间溶解时的势垒，抑制石膏的溶解。氨的浓度越高，形成的N—H···O 氢键越多，抑制作用越明显。上述机理提示，石膏宏观溶解速率应与溶液的氨浓度相关。尽管微观反应机理尚难于表征，但宏观效应可以通过不同浓度氨水溶液中石膏颗粒溶解实验数据进行关联。

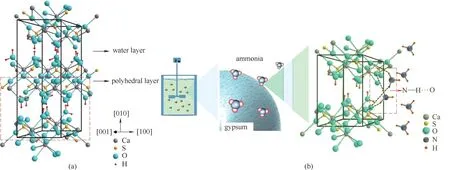
图2 氨抑制CaSO4·2H2O溶解机理Fig.2 Mechanism of dissolution inhibition of gypsum by ammonia

1.2 石膏颗粒群溶解速率模型

对溶解过程各主要组分进行物料衡算。

总钙、硫守恒

总氮守恒

电荷守恒

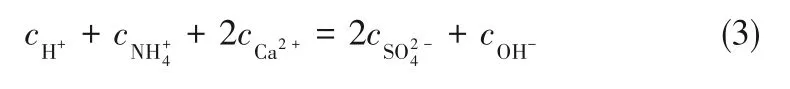
当溶解为表面反应控制时，以质量m 随时间的变化表示石膏颗粒的溶解速率[23]

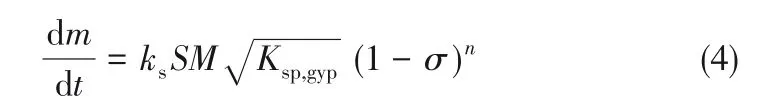
式中，S 为石膏颗粒的表面积，m2；M 为CaSO4·2H2O 的分子量，172.17 ；ks为速率常数，m·s-1; Ksp,gyp为CaSO4·2H2O 的溶度积常数，4.23×10-5mol2·L-2；n为溶解反应级数，无量纲；σ 为液相主体饱和度，其定义[12]如下

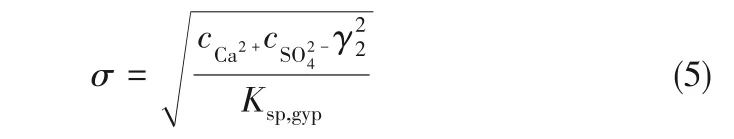
以与石膏颗粒等体积的球体直径作为颗粒的特征粒径L，则石膏颗粒的体积和表面积[24]如下

式中，ρ 为石膏颗粒的密度，2.32 g·cm-3；φV为体积形状因子，π/6，无量纲；φS为面积形状因子，5.40[25]，无量纲。基于文献[26-27]报道，并联立式(4)～式(7)，则表面反应控制下石膏颗粒的溶解线速率方程为

式中，rl为溶解线速率，μm·s-1；k 为本征表面反应速率常数，mol·m-2·s-1；γ2表示二价离子的活度系数，无量纲，其值可根据Davies 方程求解[28]。则溶解速率方程ra可表示为

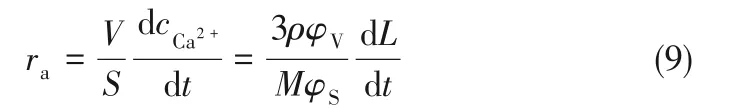
式中，ra为溶解速率，mol·m-2·s-1。假设溶解线速率rl与颗粒特征粒径L无关，将石膏颗粒数密度函数f(L,t)对时间和特征粒径偏微分，建立溶解种群平衡方程[29-30]

式中，Vl为液相的体积，L。

综上，建立了氨介质中石膏颗粒溶解速率模型，并用MATLAB R2004a软件进行数值求解。溶解种群平衡方程求解的流程如图3所示。

图3 溶解种群平衡方程求解框图Fig.3 Calculation flow chart of dissolved population equilibrium equation

2 实验材料和方法

2.1 实验试剂与仪器

试剂：雪花石膏矿石(广西，桂林)，CaSO4·2H2O的含量大于99%；氨水(AR,成都市科隆化学品有限公司)；实验用水为去离子水。

仪器：激光粒度分析仪(Malvern®，Spratec 喷雾分析系统，测量精度＞1% ，英国马尔文仪器有限公司)；搅拌器(IKA®EUROSTAR 20 digital，测量精度±1 r·min-1，艾卡(广州)仪器设备有限公司)；钙离子电极(Pca-1-01，测量精度±0.5%，上海仪电科学仪器有限责任公司)；pH 电极(E-301-D，测量精度±0.002 pH，上海仪电科学仪器有限责任公司)；恒温水浴锅(XOSC-15D，测量精度±0.5℃，SINO TECH)。

2.2 石膏颗粒制备与初始粒度分布

将雪花石膏矿石粉碎并筛分出75～125 μm 的石膏颗粒作为研究对象，用激光粒度分析仪测量其初始粒度分布。颗粒特征粒径采用等体积球体直径。粒度分布密度函数v(L,t)由相应粒度区间内颗粒体积所占总体积的百分数表示，通常为对数正态分布

其与种群平衡模型中的数密度函数f(L,t)的关系式为

图4表示测量所得石膏颗粒相应密度分布曲线v(L,t)及对数分布函数拟合结果和相应数密度函数f (L, t)曲线。经拟合，其颗粒平均粒度Lave= 156.59 μm，对数方差σ2=0.235。

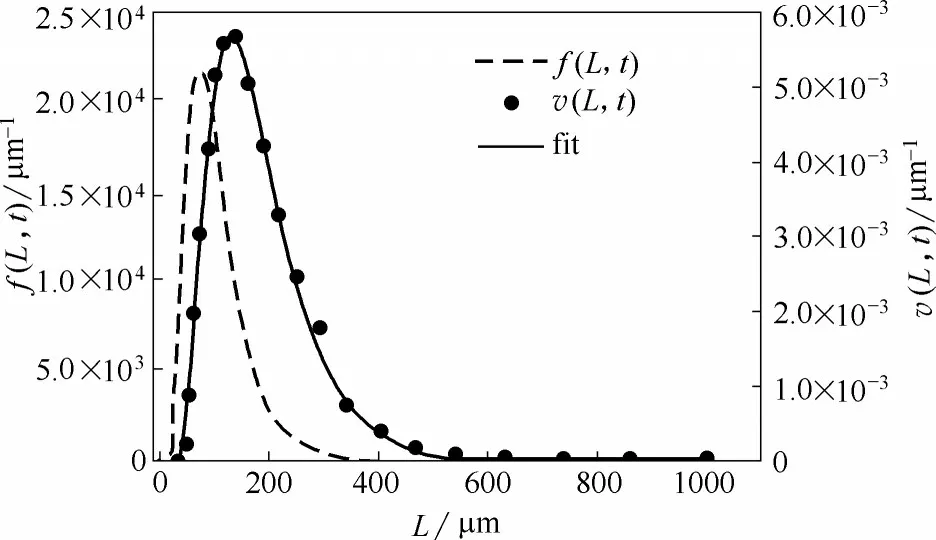
图4 石膏颗粒初始粒度分布Fig.4 The initial size distribution of gypsum particles

2.3 扩散传质阻力的消除

在间歇反应器内加入1000 ml 氨质量分数ω 为6%的氨水溶液。控制温度25℃，称量6 g石膏颗粒，一次性投料进行溶解。用搅拌器控制不锈钢搅拌桨(六桨叶平桨涡轮)的转速，用Ca2+电极在线监测(每10 s 取一次样)体系中Ca2+浓度cCa2+随时间t 的变化规律。

不同搅拌转数下cCa2+随t 的变化如图5 所示。由于体系搅拌转速较高，测量中cCa2+有小范围的波动。当搅拌转数为1000、1200 r·min-1时，cCa2+变化曲线基本重合且远大于600 r·min-1时的cCa2+变化曲线，即搅拌转速大于1000 r·min-1时液膜内扩散传质阻力远小于表面反应传质阻力，可认为溶解速率由表面反应传质控制。由此确定颗粒群溶解实验转数为1000 r·min-1。

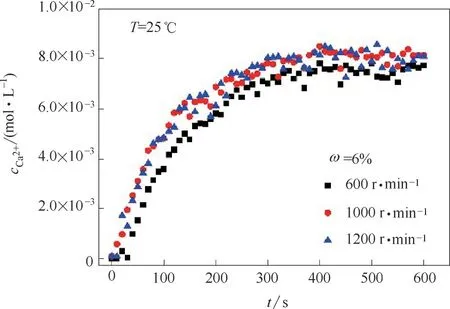
图5 不同搅拌转数下液相cCa2 +随t的变化Fig.5 Variation of concentration of Ca2+versus time with different stirring revolutions

2.4 溶解实验

实验装置如图6所示。向间歇反应器内分别加注1000 ml,ω 为0、2%、4%、6%的氨水溶液，并调节搅拌转速为1000 r·min-1。恒温水浴控制温度为15～35℃，向反应器中一次性加入6 g 筛选的石膏颗粒。溶解600 s时，纯水中钙离子浓度已近似为理论饱和浓度，钙离子浓度增加缓慢，浓度曲线已趋平(可视为溶解已达平衡)，故控制溶解时长为600 s。实验过程中用Ca2+电极在线检测Ca2+浓度、用pH 电极在线检测溶液的pH，同一组实验重复三次，取平均值。

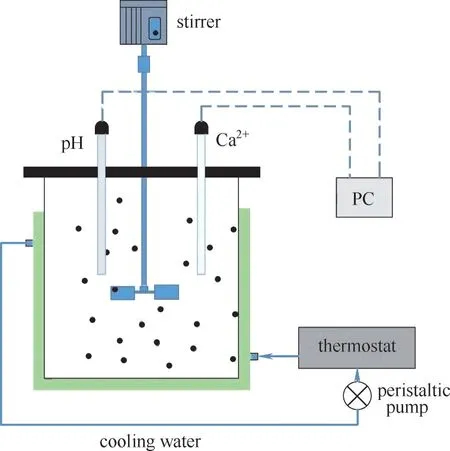
图6 实验装置图Fig.6 Schematic diagram of experiments

3 实验结果与讨论

3.1 氨浓度对Ca2+溶出速率的影响

NH3中H 会在CaSO4·2H2O 表面与上下两个双层结构间形成氢键，增大了相邻双层结构间的稳定性，同时新氢键使得氨附着在CaSO4·2H2O晶体的表面抑制溶解。在T为15～35℃、ω 为0～6%范围内，不同ω下cCa2+随时间的变化见图7。由图可知，随着时间的推移Ca2+溶出曲线的增长趋势逐渐平缓，是因为Ca2+的不断溶出增加了液相主体中Ca2+的饱和度，降低了石膏颗粒溶解传质推动力，溶出速率降低。当T 一定，纯水中cCa2+的曲线增长最快，而增大ω，Ca2+的溶出速率减小，改变反应温度，ω 增大时cCa2+曲线的变化趋势一致，氨抑制了石膏颗粒中Ca2+的溶出速率。实验结果表明，在15～35℃内，氨抑制了石膏颗粒的溶解，降低了石膏溶解速率。

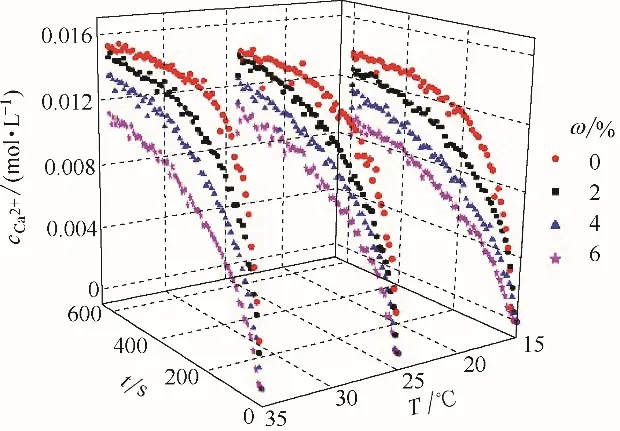
图7 不同T和ω下cCa2 +随t的变化Fig.7 cCa2 +versus t under different T and ω

3.2 氨浓度对表面反应速率常数及反应级数的影响

每隔2 min 取样得到cCa2+实验值cCa2+,exp，利用fmincon 函数拟合T=25℃下石膏溶解本征表面反应速率常数k及反应级数n。利用拟合所得的k和n值求解每一时刻溶液中cCa2+理论计算值cCa2+,cal。T=25℃时，不同ω 下石膏颗粒溶解反应速率常数k、反应级数n 和cCa2+变化见表1。cCa2+,exp与cCa2+,cal较为吻合，前2 min 偏差在10%～12%之间，其余偏差均在10%以内，验证了模型的可靠性。反应级数n 在1.10～1.13 之间，均值为1.12，表现为拟一级特征，与Jeschke 等[26]所测反应级数1.2 ± 0.2 相近。当ω 由0提高到6%时，本征表面反应速率常数k由1.73×10-4mol·m-2·s-1减小到0.46×10-4mol·m-2·s-1。实验结果表明，T=25℃时，增大氨浓度会抑制石膏颗粒的溶解，降低了石膏的溶解速率。

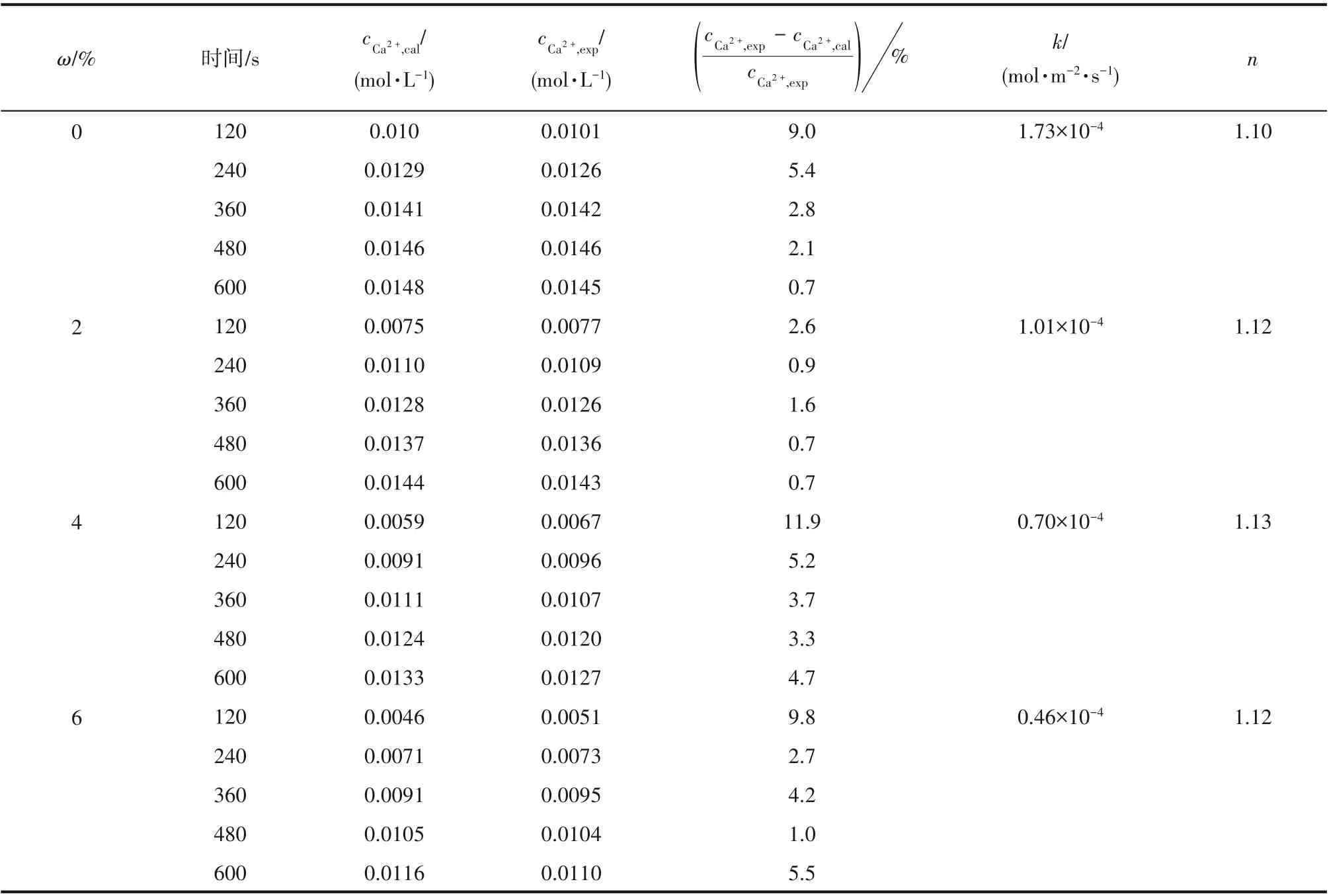
表1 溶解动力学参数及Ca2+浓度实验值与模型计算值对比（T=25℃）Table 1 Dissolution kinetics parameters and comparisons between experimental results and model calculations of Ca2+concentrations（T=25℃）

3.3 氨浓度影响下石膏的溶解速率方程

氨抑制石膏溶解的微观作用机理尚难于表征，氨对石膏溶解的宏观效应可将氨浓度与溶解数据关联进行表达。拟合k与ω，其关联表达式为

将n 的平均值和式(19)、式(5)代入式(9)，可求得温度为25℃、ω为0～6%范围内，石膏溶解速率方程

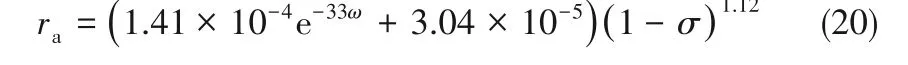
当ω=0、σ=0 时，速率方程式(20)所得溶解速率ra=1.71×10-4mol·m-2·s-1，与文献[25]报道值1.91×10-4mol·m-2·s-1相近。溶解速率ra的理论值与实验计算值的对比如图8所示，吻合度较好，最大相对偏差＜11.03%。溶解刚开始时，溶解速率绝对值最大，氨浓度对溶解抑制效果也最明显。当σ=0，ω由0增加至2%时，ra从17.14×10-5mol·m-2·s-1变为10.33×10-5mol·m-2·s-1，减小了6.81×10-5mol·m-2·s-1，而随着溶解进行，饱和度的增加使得溶解速率逐渐减小，氨浓度对溶解的抑制作用也相对减弱，当σ 上升至0.9，ω 由0 增加至2%时，ra从1.30×10-5mol·m-2·s-1变为0.78×10-5mol·m-2·s-1，减小了0.52×10-5mol·m-2·s-1。氨对石膏溶解的抑制作用不会一直增大，随着ω 的继续增大，ra曲线的变化趋于平缓，增加单位浓度的氨，ra的减小幅度降低。当σ=0，ω由2%增加至4%时，ra从10.33×10-5mol·m-2·s-1变为6.81×10-5mol·m-2·s-1，减小了34.08%，而ω 由4%增加至6%时，ra从6.80×10-5mol·m-2·s-1变为4.99×10-5mol·m-2·s-1，减小了26.6%；在高饱和度下也呈现同样的规律，当σ=0.9，ω 由2%增加至4%时，ra从0.78×10-5mol·m-2·s-1变为0.52×10-5mol·m-2·s-1，减小了33.3%，ω 由4%增加至6%时，ra从0.52×10-5mol·m-2·s-1变为0.38×10-5mol·m-2·s-1，减小了26.9%。加入氨介质后，氨与石膏颗粒形成新的N—H…O 氢键抑制了石膏的溶解。但石膏颗粒表面形成新氢键的位点有限，较低氨浓度时，可形成新氢键的有效位点多，增大单位浓度的氨，形成的氢键数目也多，随着氨的不断加入，空余的有效位点减少，增大单位浓度的氨，形成的氢键数目也少，故随着氨浓度的增大，增大单位氨浓度时石膏溶解速率的减小幅度变小。

图8 ra 实验值与拟合方程计算值的对比Fig.8 Comparisons of ra between experimental values and calculating results

3.4 三相流化矿化反应系统物料停留时间预测

石膏颗粒溶解速率可用于计算石膏颗粒溶解所需的停留时间，是磷石膏矿化CO2三相流化矿化反应器(图1)的设计依据。假设石膏为均匀分散的规则球形颗粒，则其完全溶解所需停留时间t 可由溶解线速率rl和粒径L求得

石膏颗粒溶解掉的体积Vdis与颗粒总体积Vsum的比值为溶解率w，则

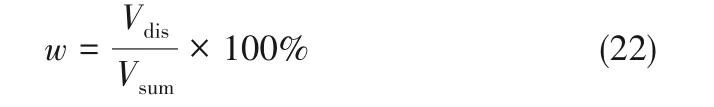
联立式(8)、式(21)和式(22)，可求得25℃下、不同粒径颗粒停留时间和溶解度的关系。将三相反应器中的石膏颗粒群按粒径从大到小，划分成等质量的10 等份，每等份的等比表面积平均粒径最小为58 μm，最大为446 μm。石膏颗粒群在三相矿化反应系统中微量氨浓度(ω=0.6%，σ=0.9)的尾气吸收循环回路中，处理含氨尾气至氨含量不高于10-5，石膏颗粒完全溶解的停留时间如图9(a)所示；而在高氨浓度(ω=6%，σ=0)的矿化结晶循环回路中，磷石膏颗粒群与烟气和高浓度氨气混合气完成矿化反应，转化磷石膏96%、吸收CO280%以上，石膏颗粒完全溶解的停留时间如图9(b)所示。

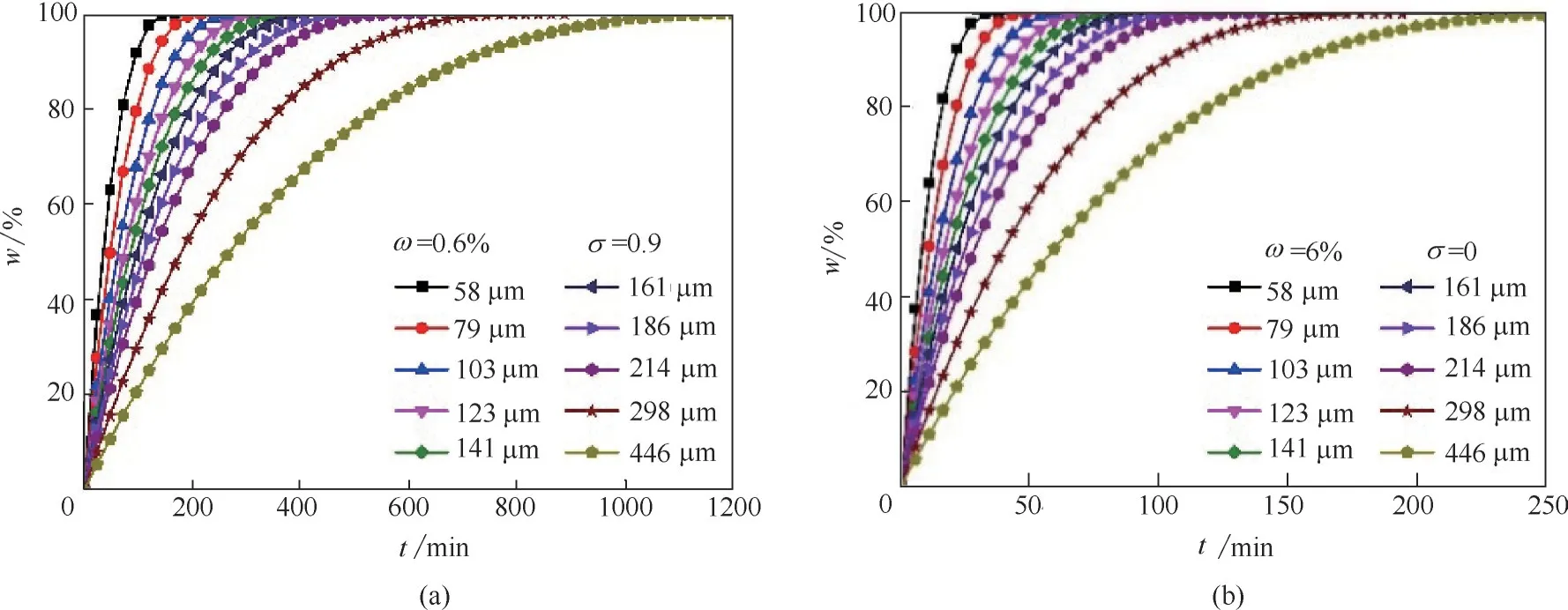
图9 不同粒径颗粒w随t 的变化Fig.9 Variation of w versus twith different particle size

将不同粒径的石膏颗粒溶解率加权求和，即可得到石膏颗粒群的总溶解率和停留时间的关系，如图10所示。三相流化矿化反应系统中，石膏颗粒先在尾气吸收(ω 约为0.6%)循环回路溶解7%，而后进入下一矿化结晶(ω 约为6%)循环回路进行三相反应，使石膏转化96%以上。采用氨影响下的溶解速率计算，石膏颗粒需在尾气吸收循环回路停留约11 min(A点)，而采用纯水中的溶解速率，石膏颗粒需停留约9 min(B 点)，两者相差2 min；采用氨影响下的溶解速率计算，石膏颗粒需在矿化结晶循环回路停留约86 min(C 点)，而采用纯水中的溶解速率，石膏颗粒需停留约24 min(D 点)，两者相差62 min。可见，以纯水中石膏颗粒的溶解速率计算停留时间，石膏颗粒群的实际转化率仅为33%。因此，基于氨介质影响下石膏溶解速率模型，可有效预测三相流化矿化反应系统两个串联回路石膏浆料所需的停留时间，为磷石膏-氨-水固碳体系直接矿化烟气CO2的放大设计提供了理论支撑。