基于核心素养的初中几何入门教学实践探究——以“三角形内角和定理及其推论的应用”教学为例

□福建省连江县凤城中学 郑周明

作为初中教学重要组成部分，数学教学可以培养学生形成一定的数学逻辑思维能力，提高学生学习素养。基于核心素养背景下，要求初中数学教师在实际教学过程中要侧重培养学生数学逻辑能力、抽象思维以及探究意识等，从而更好地提升学生数学综合能力。值得注意的是，尽管近年来大多数学教学活动中对核心素养教育部分给予足够重视，但实际教学中仍存在较多问题。为此，本文对几何入门教学方法的分析，有着现实意义。

一、创新教学方法，提升学生的学习兴趣

在初中阶段，学生具有较强的好奇心和求知欲，只要教师稍加引导，利用合适的教学方法，促使学生产生对数学学习的兴趣。由于初中几何知识相对较难，学生难以提起学习兴趣，容易产生厌烦感、畏惧感。所以，在几何入门阶段，数学教师要着重培养学生的学习兴趣，让学生产生浓厚的求知欲望，为后续几何学习做好准备。教师可以利用贴近学生生活实际的案例，吸引学生的注意力，利用学生熟知的事物，提高学生的兴趣。

例如，在教学“三角形内角和定理及其推论的应用”这一内容时，教师可以先为学生展示放风筝活动的图片或者视频，吸引学生的注意力，而后提出具体问题引发学生思考：“如图1 所示，这是一位学生设计的风筝，请说一说此形状的特征？”“能否通过添加辅助线把它转化为我们熟悉的图形呢?”通过问题的引导，提高学生探究意识。由于初中阶段的学习多感性认识、形象思维为主，而教师选取贴近学生生活的题材，让学生觉得不陌生，能够有效提高学生的学习成效，提升学生的兴趣。

图1

二、立足几何图形，循序渐进教学

进入题目后，教师要逐步引导学生思考，鼓励、激发学生的求知欲，利用学生的好胜心理，在探究过程中，不断增强学生信心，促使学生可以在教学活动中充分展示自我，感受学习数学的成功与快乐，激发同学们对知识的强烈渴望，营造出浓厚的数学学习氛围。但是在实际教学过程中，需要数学教师将基础图形作为教学的基本，在此基础上，由浅入深地展开教学，帮助学生建立清晰的解题思路，促使学生的迁移能力得到提高，将知识转化为能力。

还是以上文教学为例，教师引导学生将图像转化为以往学过的基本图形，学生会通过做辅助线的方式，得到如图2所示图形，此种方法称为“化归”法，利用此种方法，可以更好地帮助学生理解问题，并将复杂化的图形简单化，有利于探究图形的性质。而后，教师可以进一步向学生提出问题：“大家能找到∠BDC 与∠A、∠B、∠C 之间的关系吗?”引导学生深入探究。经过详细的研究，学生得出了此题目的验证结果：∠A+∠B+∠C=∠BDC。

图2

三、启发学生的数学思维，提升学生理解几何的能力

通过上文题目的分析后，数学教师需要启发学生的数学思想，通过引导，提高学生对数学问题的进一步认识。比如，教师可以引导学生从多种角度去分析问题，让学生发散思维、创新方法，解决上述题目。在学生创新的过程中，无论正确与否，教师都要注意教学语言的使用，要鼓励学生，不要打击学生，以免影响到学生学习几何的积极性。

例如，教师对风筝模型进行了加工，如图3 所示，向学生提出了问题：1.图中还存在图1 中的四边形么?一共有几个？2.如果∠A=∠B=∠C=∠E=∠F，那么∠1 为多少度？

图3

图3是一个五角星的形状，由图1的凹四边形构造而成，但在图中增加了FE、FD、DE三条线，改变了原来的图形。学生经过分析和思考后，发现了基本图形ABDC，随后就找出了五角星的各个定点对应的图形就是凹四边形。而对于第二个问题，由于五角星五个角的和为180°，所以，学生会得出∠A=∠B=∠C=∠E=∠F=36°，但并不能很好地算出∠1 的度数。主要是因为学生对基本图形的性质理解还不到位，从而导致在解题时无法加以运用。在此过程中，教师则要发挥出指导作用，启发学生的数学思维，引导学生将题目中的基本图形性质运用起来，而后，学生便得出了∠1=∠A+∠B+∠C，最终得出∠1为108°。通过数学思维的引导，有效提高了学生数学知识的运用能力。

四、养成良好的学习习惯，提高学生的思维品质

在新课程标准的改革下，培养学生学科素养已经成为当下教育的重要方向，而在初中几何数学中培养学生的思维品质，在有限的课堂中实现最大化的数学教学，成了广大教师不断努力的方向和目标。良好的学习习惯和思维品质不是与生俱来的，而是后天教育培养的结果，需要教师积极地引导和培养。

比如上文提到的在探究圆规四边形性质的过程中，数学教师通过一题多解的方式，促使学生在固有思维定式基础上，引发学生发散思维从多种角度、各个侧面、不同方向去思考问题，这为学生书数学思维习惯的养成提供了良好的基础。例如，已知，图4 中，在圆规四边形ABCD 中，∠BDC 为140°，如果∠ABD,∠ACD 二者的角分线相交于点E，其中∠BEC 为77°，问∠A 是多少度？而如果∠ABD,∠ACD三等分点交于点E1、E2，那么，如图5所示，∠BEC为77°，此时∠A是多少度？

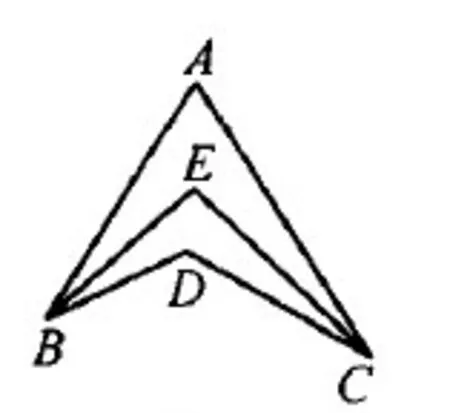
图4

图5

在这个几何题目中，所有的图形都由基本图形组合而成，通过全面的分析，学生已经具备了一定的学习经验，所以可以很快地分析出题目所要表达的意思并求得其中的基本图形，在此基础上进行解答。在学生解答过程中，教师要对学生的表现给予充分肯定，鼓励学生积极探索，进行深层探索，对新颖独特、创造性的解法给予肯定，而后以小组合作的方式促进学生之间在思维上的交流，培养学生合作能力，进而得出了正确的结论。通过此题目中相互关联的问题，促使学生进行深入探究，不仅提高了学生基本图形的应用能力，同时也极大地加强了学生归纳、类比的数学思想，有利于实现培养学生积极探究的良好品质和良好的认知结构。通过对圆规四边形性质的应用，促使学生由表及里地去观察、去思考其中的数学关系，引导学生提取出问题的核心，揭示问题的规律，帮助学生更好地将数学知识进行深层渗透，培养学生思维的全面性和深刻性。

五、结语

综上所述，数学几何作为初中数学的重要组成部分，教师通过有效的教学方法，可以提升学生的数学思想、探究能力，这与核心素养教学目标不谋而合。因此，在初中数学教学中，教师需要通过创新教学方法，提升学生学习兴趣，立足几何图形，循序渐进地教学，提升学生数学思维能力，提高学生理解能力等途径，全面培养学生数学核心素养。