数据：“以学定教”的底气

江苏南京市天景山小学 梅玉华

《解决问题的策略——画线段图》是发展学生几何直观能力的重要教学内容。学生要学会画图描述问题，能借助直观图分析问题；体验借助几何直观，可以把复杂的数学问题变得简明、形象，有助于直观地理解数学，探寻解决问题的思路和方法；继而提高分析和解决问题的能力，积累解决问题的经验，获得成功的体验。如何能够很好地实现这些目标，我们通过基于证据的研究进行了探索。

一、数据——让学情分析定量化

为了解决这些问题，构建以学定教、学为中心的课堂，我们针对四年级学生使用画图来解决问题的意识和能力做了学前调研，调研（2018版）在4个基础差不多的班进行，以例题的改编题为素材，有两种样卷，一种无画图提示，一种有画图提示。

1.王明和张华共有68张贴画，王明比张华少14张，张华有多少张贴画，王明有多少张贴画？（提示：如有需要，画一个线段图，再解答。）

2.有一块长方形菜地，长9米，因修路占用，长减少了2米，面积减少了14平方米，这块菜地原来的面积是多少平方米？（提示：如有需要，画一个示意图，再解答。）

统计的结果如下：

?

关于前测的结果分析：

1.关于画图的意识：在没有提示时，四年级学生有一定画图意识的占13.1%;在有提示时，有一定画图意识的占28.9%，自觉性会更强，但整体画图意识不强，约占21%。

2.关于解决问题正确率：没有画图提示时正确率为42.4%，有画图提示时正确率为51.3%。画图的提示对正确率提高有影响，但是并没有直接表现在画图解答的人和正确率的增加；而不画图的正确率有大幅的提高：26/66≈39.3%到28/54≈51.8%（是否在头脑中有想象的图，还是提示让他们更仔细地去分析？）

3.关于画图方法对解题正确率的影响：画图的整体正确率为18/32≈56.3%，不画图的整体正确率为54/120=45%，对解题的正确性有一定的影响。

有趣的是，无画图提示的，画图分析的正确率为60%；在有画图的提示下，画图分析的正确率仅为54.5%，正确率下降了，这是否可以说明没有自觉画图意识的学生或没有掌握画图分析的学生，画图本身并不能提高解决问题的正确率。

4.关于学生画图方法的经验基础：有画图提示，第1题增加了7人；第2题增加了5人，说明学生有时想到画图也不知道怎么画。

基于这样的学情分析，我们将教学流程设计为让学生自己独立尝试补充线段图、根据线段图分析解答、利用线段图阐述思考过程，通过画、用线段图说来体会画图策略，进而实现“学为中心”。为了进一步了解学生真实的学习历程，检验课堂教学效果，我们还对尝试画图、解决问题的方法、口述思考过程三个方面进行了课堂观察。

2018年版：

师：今天我们要继续学习解决问题的策略。老师先请大家欣赏一些美丽的邮票，我们有两位同学也很喜欢收集邮票。（出示：小宁和小春共有72枚邮票，小春和小宁的邮票枚数同样多。两人各有邮票多少枚？）

生：72÷2=36（枚）

师：为什么可以用除法？

生：因为两人同样多，可以平均分。（板书：同样多平均分÷）

师：（出示：小宁和小春共有72枚邮票，小春比小宁多12枚。两人各有邮票多少枚？）你还能不能直接求出题中的两个问题？

生：……

师：有的同学还不会，你能帮助他们分析一下条件和问题吗？你想怎样清楚地表达出来？

生1：可以用列表的方法来整理。

生2：可以用画图的方法来整理。

师：画图可以用来整理和分析条件及问题，你们会画吗？把活动单上的线段图补充完整（学生独立补充并且板书线段图）。仔细观察一下线段图，现在你能想到解法吗？还能想到其他方法吗？

师：你能结合线段图去说说这些解法吗？（生解答汇报）

……

师：这些方法有什么相同点和不同点？你是怎样想到的？（生口述）

师：现在，你对画线段图有什么体会？

问题及调研：

教研组的教师感觉这节课进步很多，存在的主要问题是学生对画图的体验没有获得理性的认识。为了更加全面地认识学生的学习过程，课后我们对观察的数据进行了整理分析。

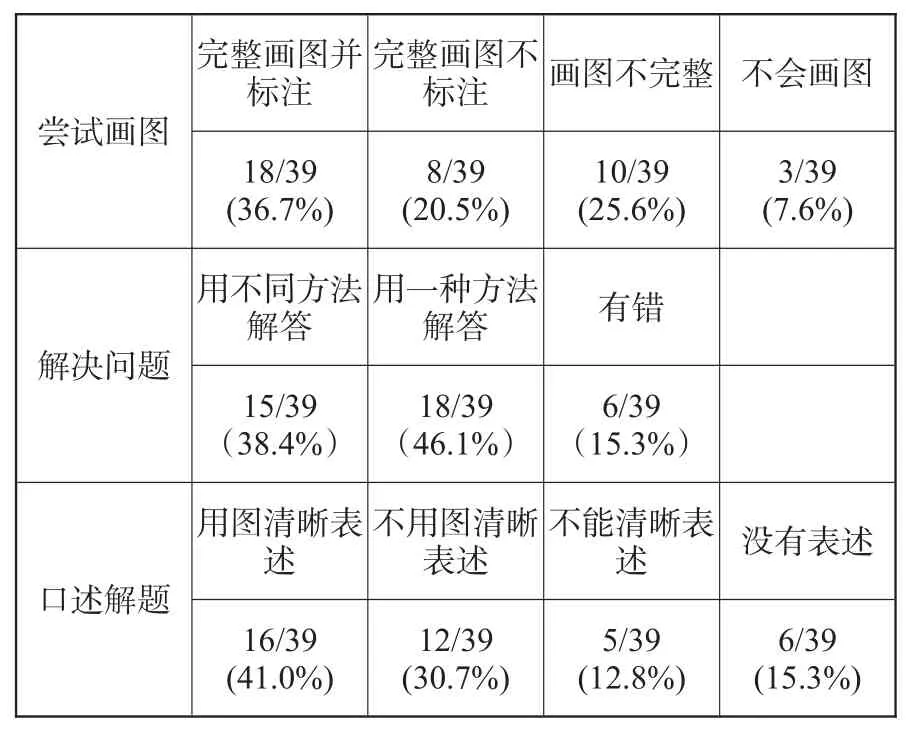
完整画图并标注完整画图不标注画图不完整不会画图尝试画图18/39(36.7%)8/39(20.5%)10/39(25.6%)3/39(7.6%)用不同方法解答用一种方法解答有错解决问题15/39（38.4%）18/39（46.1%）6/39（15.3%）用图清晰表述不用图清晰表述不能清晰表述没有表述口述解题16/39(41.0%)12/39(30.7%)5/39(12.8%)6/39(15.3%)

1.关于补充画图的能力：从统计的结果来看，学生补充画图，正确率很高，只是在标注上存在一些问题，个别学生出现3条线段（不会解答）。

2.关于画图对解答方法的启示：在画图之后又有15/39（38.4%）的同学想到不同方法，远高于学前调研，可见线段图在启发学生解法上有一定的作用。

3.关于用图解释算法的能力：因为刚画完图，有16/39（41.0%）的学生选择用图来说，也有学生不用图说得很清楚，不知道他们脑中是否有图，还是根据数量关系来表述的。但是5个不能清晰表述的学生都没有想到用图，其中2个在提示之后用图说得比较清楚，线段图对学生分析思路的清晰度有较大的帮助。

二、数据——让数学思维分析定量化

2019年4月，我们再次研究这课，对3个水平相近班级进行了学前调研。

1.公鸡和母鸡一共有80只，公鸡的只数是母鸡的三倍，公鸡和母鸡各有多少只？

2.王明和张华共有68张贴画，王明比张华少14张，两人各有多少张贴画？

调研时我们用了三种不同的形式呈现：文字呈现（无提示）、文字呈现（要求画图）、线段图呈现。文字呈现（无提示）、线段图呈现时鼓励学生用不同方法解答。前测的结果分析：

1.关于线段图对解题正确率的影响：当题目以文字的方式呈现，学生的正确率为82.9%；当要求画图时学生的正确率为90.6%；当以线段图呈现时正确率为100%，表明线段图对解题正确率有较明显的提高作用。

2.关于补充画图的能力：从统计的结果来看，学生画图的正确率很高，只是在标注上存在一些问题，与课堂观察结果一致。

3.关于线段图对解题方法的影响：当鼓励学生去思考不同解答方法时，线段图呈现（18.9%）与文字呈现（2.4%）对学生的不同方法解答的影响有明显差异。比对课堂观察的结果38.4%，线段图对学生解法的启发在时间较短时，影响不是那么明显。

基于以上的分析，我们想让学生尝试独立画图，学生独立借助图思考不同解法，学生小组述说分析思路，构建真正的“学为中心”的课堂，设计教师通过三次比对：文字与图呈现条件与问题的比对；原来不会到会、到多种解答方法的比对；直接说想法与借助图说想法的比对，让学生体验画线段图的策略，体会线段图有助于我们去分析数量关系、整体性把握分析方向、直观述说分析思路。

2019年版：

师：今天我们要继续学习解决问题的策略。老师先请大家欣赏一些美丽的邮票，我们有两位同学也很喜欢收集邮票。（出示：小宁和小春共有72枚邮票，小春比小宁多12枚。两人各有邮票多少枚？）

师：（检查学生举手情况）看来有的学生还不会，需要帮助他们分析一下条件和问题呢。你想怎样表达这些条件与问题？

生1：可以用列表的方法来整理文字。（板书）

生2：可以用画图的方法来整理。

师：画图可以用来整理和分析条件和问题，你们会画吗？（学生独立画图并板书）

师：这个图能表示出所有的条件和问题吗？（完善线段图）你能根据线段图，说出这道题的条件和问题吗？

生：小宁和小春共有72枚邮票，小春比小宁多12枚。小春有多少枚邮票？小宁有多少枚？

师：看来用文字和线段图都可以整理条件和问题，比较两种方法，你想说什么？

生：画线段图直观一些，清晰一些。

生：……

用文字和线段图来整理条件和问题是两种常用的方式，相对文字而言，线段图更直观一些。通过刚才的整理条件和问题，你现在会解答吗？（追问原来不会的同学）

师：仔细观察线段图，想想其中的数量关系，你有没有想到别的方法，选择其中的一种进行解答，再利用你画的线段图把你的方法说给小组的同学听。

……（学生独立完成并汇报，学生评价）

师：看来线段图不仅可以帮助我们去想问题，还可以帮助我们清楚地把自己的解法说给别人听，这些方法有什么相同点和不同点？

……

师：现在，你对画线段图有什么体会？

这节课学生表现很主动、很精彩，特别是对线段图的作用体会很深刻。

三、研究反思

1.读懂学生是“以学定教”的起点

奥苏伯尔在《教育心理学》中指出：“如果我们不得不将教育心理学还原为一条原理的话，我将会说，影响学习的最重要因素是学生已经知道了什么，我们应当根据学生原有的知识状况进行教学。”在“以学定教”的课堂，了解学生的学习起点尤为重要。学前调研的数据，让我们对学生学习起点有一个定量的了解，为我们的“以学定教”提供了基础，给教师（特别是青年教师）提供了一条科学了解学生知识状态的途径。

2.读懂教材是“以学定教”的基础

读懂教材要透彻地了解数学知识的价值，了解知识对学生思维产生的影响，发现学生体验、感悟数学内涵的通道，是真正实现“以学定教”的重要保障。“以学定教”的“学”不仅仅是指学生的起点，还包括学习的知识、学习知识的通道。学前调查、课堂观察数据的整理与分析为我们提供了分析手段，这样才能真正实现“以学定教”“学为中心”。

袁振国教授曾提出：“实证研究首先是一种精神，一种研究规则，一套方法体系，是精神、规则和方法的有机结合。”一线教师进行实证性的教研会培养其理性精神，帮助其真正建立“以学定教”的意识，这是我们实现“以学定教”，构建“学为中心”课堂的底气。♪