上证指数预测效果实证分析

柴武越，万光彩，张天圆

(1.安徽财经大学 金融学院，安徽 蚌埠 233000；2.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233000)

一、引言

随着我国经济的繁荣发展，我国股市发展迅速，股民投资需求旺盛，发展前景良好。但由于我国金融行业的快速发展，我国股市现阶段存在功能导向性不足、股市受政策、其他行业影响较大、市场机制不够成熟、很多上市公司股票质量不够高等问题。而我国大部分股民缺乏专业的金融知识，投资不够理性，购买股票时爱跟风、无主见，投机性目的很强，很容易因为各种不利信息的出现做出快速退出市场的操作，这使得众多股民很容易投资失败，这些不当操作也加剧了我国股市的动荡。由于我国股市的发展已经超过传统模式下的预测范畴，股民对股市发展的判断存在较大困难。因此加强对我国股市的预测分析，提供更为精准的预测方法，有利于缓解现阶段我国股票市场存在的问题，促进股票市场有序运作，更好地服务于众多投资者。

二、文献综述

在预测我国股市行情时，最常运用的指标是上证指数，上证指数即上海证券交易所综合股价指数，是一种反映上海证券交易所股票总体走势的统计指标，对其进行科学预测可以更好地了解股市未来的波动情况。我国众多学者运用了不同模型方法对上证指数进行预测。王玥等人运用集成算法对股票指数进行预测，得到了集成算法可较好地对股票指数进行短期预测的结论。在集成算法的不同方法中，Random forest 对上证指数的预测效果更强[1]。马艳娜等人基于ARIMA 模型对上证指数收盘价进行预测，同样得出该模型对股票的短期预测有较好效果[2]。林春秀等人运用主成分分析、BP 神经网络模型预测大盘涨跌幅，得出该模型可较精准地预测上证指数的涨跌情况[3]。李姣运用ARMA-ARCH 模型对上证指数收益率进行预测，消除了序列的线性依赖及ARCH 效应[4]。

各文献表明，众多模型与方法皆可以对上证指数进行预测来估计股市的走向，但哪种模型能更准确地预测股市的未来趋势却没能更好地确定。在预测模型的应用中，ARIMA 模型及指数平滑模型的操作更简单，不需要借助其他外生变量进行模型预测，可以较好地反应市场变化的规律和水平，因此本文将通过对比ARIMA 模型及指数平滑法对上证指数的预测效果，总结出更易于预测股市变动的方法，进而对我国股市发展及股民的投资起到指导作用。

三、实证研究

(一)数据采集

本文选取了2016 年1 月4 日至2019 年12 月20 日除去节假日的每日收盘的上证指数作为样本数据，运用ARIMA 模型及指数平滑法通过共968条数据对未来股市变动进行短期预测，得出更精确的结论指导股民投资、引导股市发展。

(二)平稳性检验

由于股市中个股存在较大的波动及差异，用上证指数反映股市状况能更系统地预测股市走向。同时在较长期限内上证指数的波幅较大，是非平稳的时间序列，因此本文将对序列做平稳化处理。得到平稳化序列后，则可以用于ARIMA 模型及指数平滑模型的构建。经过一阶差分后，可以得到序列即：

用SPSS 软件做出一阶差分后的时序图，由图可见一阶差分后的时间序列在零上下波动，因此该序列是平稳的。

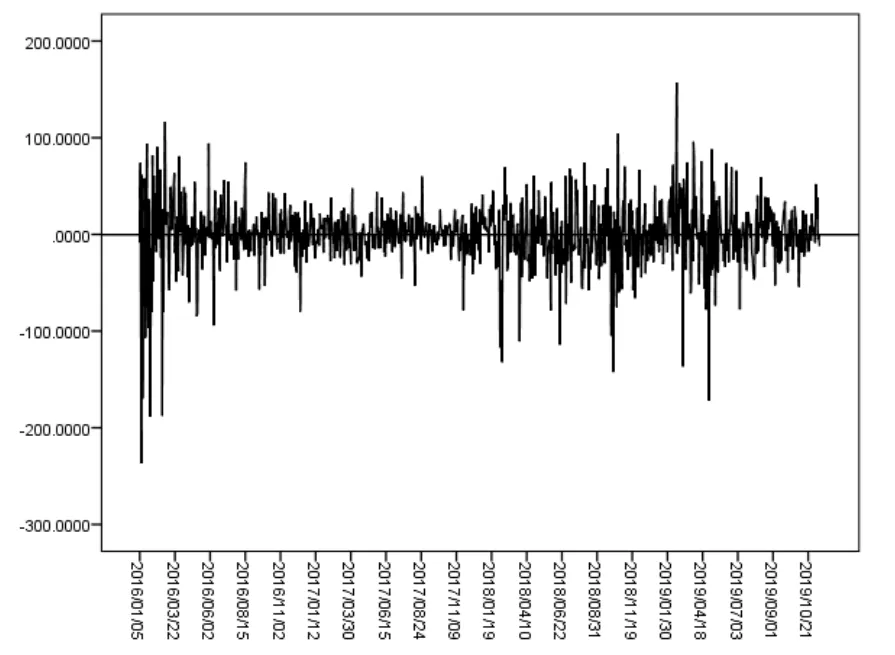
图1 一阶差分后的时间序列图

为确认序列的平稳性，还需对处理后的时间序列进行单位根检验。若检验其k 阶单位根存在，则说明平稳性检验不能通过，模型无法建立。对该序列的检验做出原假设：该序列是不平稳的时间序列。经过检验后能够看出，t 统计量的值为-33.42996。单位根检验的临界值在1%、5%、10%这三个显著水平下，分别为-3.436899、-2.864320、-2.568303，均大于t 检验的统计量，所以拒绝原假设，该序列是平稳的时间序列。

对时间序列做一阶差分处理，我们可以得到平稳的时间序列。本文将分别使用ARIMA 模型及指数平滑法对所得数据进行预测并检验其预测效果，进而得出结论。

(三)ARIMA 模型的构建

ARIMA 模型即差分自回归移动平均模型，它将原始数据看作一个随机序列，通过建立数学模型来描述这一序列，并对该序列值进行预测[5]。ARIMA 模型要求时间序列是平稳的，若原时间序列不平稳，则要求差分化后该序列平稳，并使用处理后的数据构建模型。

由于我们已经得到了平稳的时间序列，则可以通过ARIMA(p,d,q)模型对数据进行建模。将模型进行定价处理，可以得到平稳时间序列差分阶数为d=1。通过观察自相关与偏相关图，可知偏自相关系数和自相关系数都是4 阶截尾，可以初步估计ARIMA 模型的自回归阶数为4，移动平均阶数也为4，我们选择BIC 最小的模型进行定阶，所以最终确定当时，其正态化的BIC 值最小，其值为7.029，所以可建立ARIMA(1,1,0)模型。

基于时间序列ARIMA(1,1,0)模型对数据进行拟合，并通过调整参数，使模型通过显著性检验，得到更为准确的时间序列预测模型，模型的参数估计结果如表1 所示。

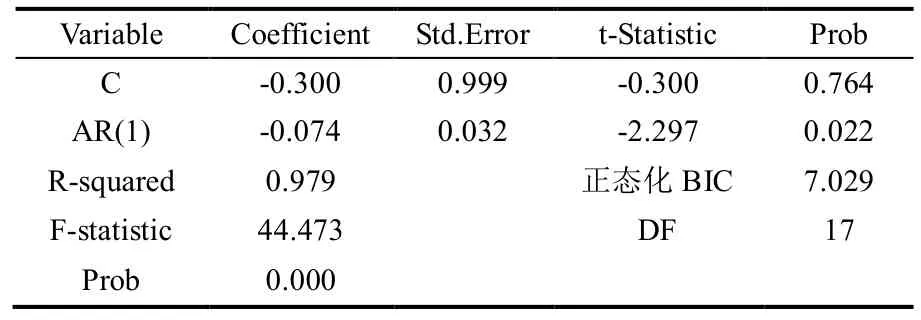
表1 ARIMA(1,1,0)模型参数估计表

由参数估计结果可以看出除常数项以外，自回归项的参数估计系数的P 值小于0.05，在5%的显著性水平下是显著的，由此得到的ARIMA(1,1,0)模型表达式为：

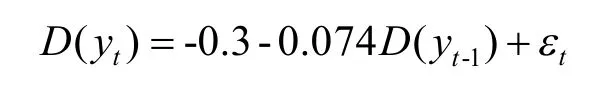
将表达式转换后为：

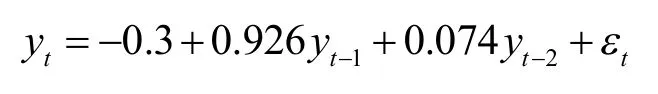
其中yt-1表示原时间序列滞后一期的序列，yt-2表示原时间序列滞后二期的序列。

对残差序列进行白噪声检验，能够验证模型建立的合理性。因此，本文将使用SPSS 软件对模型进行检验，并通过分析ARIMA(1,1,0)模型残差的自相关图和偏相关图，来验证模型的相关性及变量的随机性。如图2，检验结果显示残差序列的自相关和偏相关在两倍标准差内，该模型的随机误差项为白噪声序列，检验很好地通过，证明模型的结论是有效的。

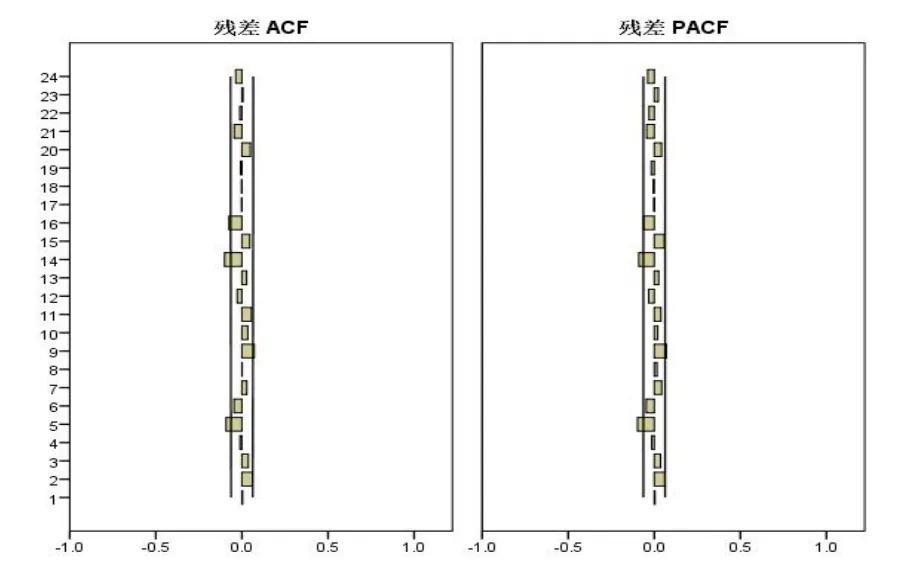
图2 残差相关图

同时，为了更准确地对残差进行白噪声检验，本文将对残差序列进行方差齐性检验。首先将对残差序列进行正态检验，再根据其分布性质选择恰当的方差齐性检验方法。对残差分布频率直方图进行分析后，可以发现残差序列并不符合标准的正态分布，因此本文将对残差序列按月份分组，并使用Kruskal-Wallis 非参数检验对残差序列进行方差齐性检验，检验结果如表2 所示。

表2 方差齐性检验表

该检验的原假设为残差序列具有方差齐性，检验所得的显著性P值=0.319＞0.05，说明原假设成立，方差齐性检验通过。

因此该模型的残差序列为白噪声序列，模型已经将时间序列中的有效信息全部提取，该时间序列模型有效。

(四)指数平滑法的构建

本文在建立ARIMA 模型以外，还通过建立指数平滑法对时间序列进行分析和预测。简单指数平滑法，给予了不同时间上的数据不同的权重，每次平滑后得到的数据都是由过去数据加权求和后得到的，因此越接近当期时间的数据对该模型预测结果影响越大，同时该模型要求时间序列不能含有趋势成分及季节成分。

观察原时间序列的时序图，可以看出原数据不存在季节性特点，可能存在较低的趋势特点，同时股票的涨跌趋势更易受近期股票市场状况的影响，因此指数平滑法适用于对上证指数的预测。而阻尼趋势的指数平滑法可以预测包含趋势因素的序列，同时加入阻尼效应也可以减弱线性的趋势，适用于对上证指数的预测。

所以本文根据这些特点分别建立简单指数平滑模型和阻尼趋势的指数平滑模型，其参数估计如表3 所示。

表3 指数平滑法的参数估计结果表

由上表可以看出，简单指数平滑模型水平的平滑参数在1%的显著性水平下通过检验，而阻尼趋势的指数平滑模型的趋势平滑参数和阻尼参数没有通过显著性水平，并且其正态化的BIC 数值比简单指数平滑法的BIC 数值要小，简单指数平滑模型的表达式为：

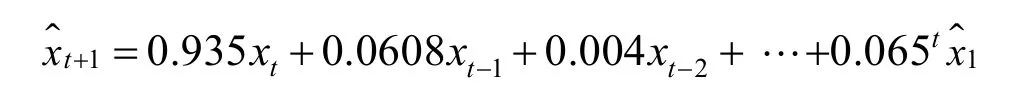
阻尼趋势的指数平滑模型的表达式为：

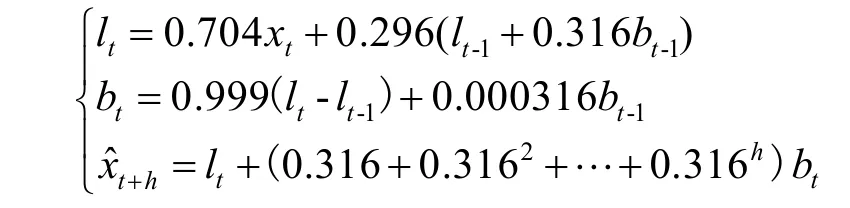
(五)上证指数的预测

我们已经构建了ARIMA(1,1,0)模型和指数平滑模型对上证指数进行拟合，下面我们将对上证指数做后几日的预测，通过对预测结果与真实数据的对比，更好地验证模型的精确度并判断对上证指数预测效果更好的模型。最终得到的模型则可以应用于上证指数的预测，为股民的投资决策提供更可靠的依据。

本文对2016 年1 月4 日至2019 年12 月12日的上证指数进行建模，得到ARIMA(1,1,0)模型、简单指数平滑模型、阻尼趋势的指数平滑模型三个预测模型，接着将用这三个模型分别对2019 年12 月13 至20 日中6 个工作日的交易数据进行模拟预测，并计算出三个模型预测的误差比，三个模型中绝对误差比平均值最小的模型则为预测上证指数更为合理的模型。模型的预测结果如表4 所示。

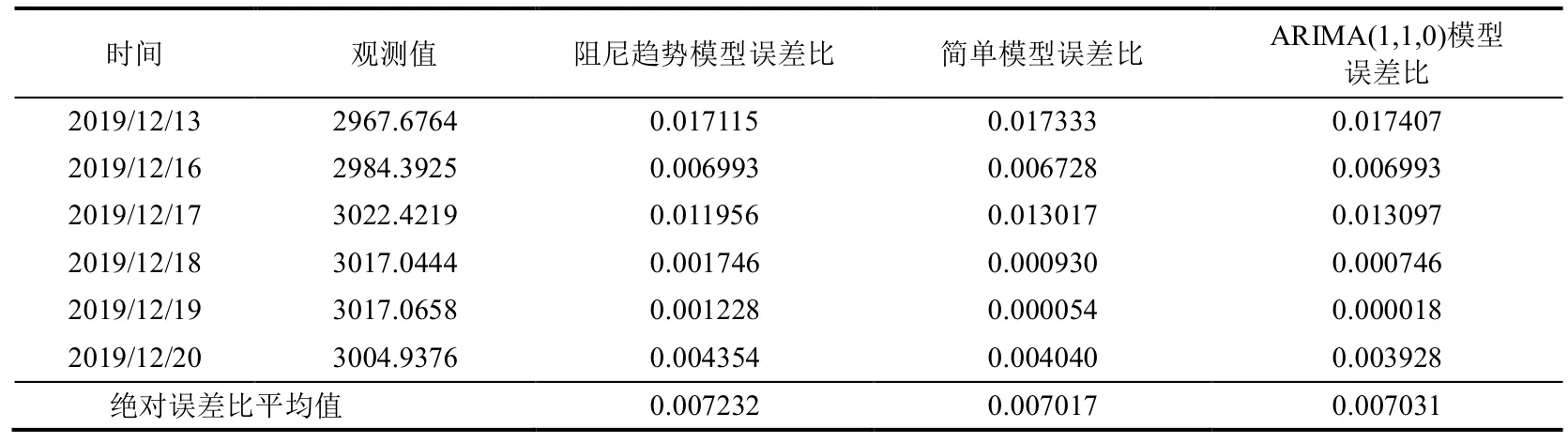
表4 上证指数观测值与模型预测值的比较

从上表可以看出，三种模型预测的拟合效果都非常好，各个模型的误差比都比较低，与实际值高度吻合，因此三者都可以较好地实现对上证指数的预测。但是对比三者的预测误差，相比于阻尼趋势的指数平滑模型和ARIMA(1,1,0)模型，简单指数平滑模型的预测误差率较低，平均小于1%，说明对于已有的上证指数数据集，简单指数平滑模型的预测效果较好，同时也能更准确地展示股市的变动趋势，对于投资者的决策起到良好的指导作用。

通过模型的特点及股市的特点，我们可以得出简单平滑指数模型在预测效果上优于ARIMA 模型及阻尼趋势的指数平滑模型的原因。首先，ARIMA模型在预测上证指数时要求数据的稳定，但它忽略了外界因素对股票市场的影响，而股市很容易受到政策或时事的影响而产生波动，这就导致ARIMA模型的预测存在误差。

同时，股市的涨跌并没有长期的或线性的趋势，规律性不强，这也使ARIMA 模型及阻尼趋势的指数平滑模型对上证指数的预测效果不佳。而股市虽然没有直观的线性趋势，但很容易因为经济政治方面的影响或股民对股市行情的信心及预期而产生在一段时间内涨跌趋势，因此使用简单指数平滑模型可以结合短期或中期内股市的情况，对股市做出更为精准的预测，它也适用于较多经济方面数据的中短期预测。

由预测结果可知简单指数平滑模型在上证指数的短期预测上有良好应用，但若预测时间加长，模型对上证指数的预测误差率会越来越大，因此简单指数平滑模型对上证指数在长期预测上仍存在不足。这是因为指数平滑模型在预测上证指数的运用上存在一定的缺陷。由于简单指数平滑模型的预测需要结合前期数列的影响，并且较早期的数据对预测结果影响较小，因此长期预测的结果并不是基于真实数据得到的，所以简单指数平滑模型不适用于对上证指数的长期预测。同时指数平滑法对转折点的处理不佳，它弱化了股市的波动情况，因此最好与其他预测方法结合使用，才能使预测的效果更好。

四、结论

本文运用ARIMA模型及指数平滑法对上证指数收盘价进行拟合和预测，得出了两个模型对于上证指数的预测皆有较好效果、而指数平滑模型能更准确地预测上证指数的结论。同时指数平滑模型对于股市的预测在短期内效果很好，对于股民的投资与股市的发展有较好的指导作用，而对于长期预测，其误差大于短期预测，因此还不适于根据指数平滑模型做出对股市投资的长期判断，还需构建更完善的模型对股市的长期预测进行深入研究。