基于遗传算法的模糊内模PID控制器优化

余 哲 王志国 刘 飞

（江南大学轻工过程先进控制教育部重点实验室）

模糊控制具有能够适用于复杂工况等特性，在各个领域得到了广泛的应用［1］。 一个模糊控制系统的控制效果，在一定程度上取决于规则表的建立和隶属度函数的选取，选取得好会使控制系统适应复杂的工业过程［2］。 传统选取规则表的方式，大多是根据工业知识、专家经验等，但因为经验的差异性使得规则表和隶属度函数的选取大相径庭，难以推广，并且过程繁琐。 因此，模糊控制领域学者关注的重点一般都在如何对模糊规则和隶属度函数进行优化上。

Karr C L和Gentry E J早在1993年就进行了隶属度函数问题方面的研究，其主要的成果是采用SGA（简单遗传算法）对论域中语言变量的模糊集进行重新设定， 构成了自适应控制系统［3］。Buckley J J认为可以优先确定隶属度函数的形状，如矩形、三角形等，然后对构成这些形状的参数进行寻优［4］。此外，Thrift P则是在固定隶属度函数的前提下，对整个模糊规则库进行寻优［5］。屈文忠和邱阳针对多变量模糊控制系统，提出采用遗传算法来设计模糊规则，这种方法不但适合非常复杂的控制系统，同时也能提高模糊控制器的鲁棒性［6］。张景元通过对遗传算法的改进，使得模糊控制系统能够在一定程度上实现规则表的自适应，并且控制效果较理想［7］。董海鹰等的研究则侧重于基于多种群的变论域方面，也实现了模糊规则的自整定［8］。 以上研究成果的不局限性是在优化过程中分别对隶属度函数和模糊控制规则进行单独处理，没有考虑到二者之间存在的内在联系， 割裂后的二者只能代表模糊控制器的一部分，因此上述方法通常只是做到了局部最优。 与上述研究不同的是，Homaifar A和McCormick E首次同时考虑隶属度函数和规则表［9］，但是却没有考虑到在进化进程中以及初始设置时可能出现的规则相互矛盾的问题，并且在整个整定过程中同时有可能出现某些值域没有被覆盖的现象，导致产生失控点。

笔者结合现有的研究成果，兼顾隶属度函数和规则表，提出了一种新的寻优算法。 其创新之处在于：将内模思想引入模糊控制，仅调节滤波器参数就可以实现对控制回路P、I、D这3个参数的调节；没有割裂隶属度函数和规则表，在优化过程中同时对两者进行寻优，从而实现控制器的整体优化；以系统的累积绝对误差作为算法的适应度函数，与传统指标相比，能够更好地反映系统的整体性能。

1 内模PID控制器原理

考虑如图1所示的单变量反馈控制回路。

图1 单变量反馈控制回路结构

图1中，G（s）和C（s）分别为过程模型和PID控制器，r（t）、e（t）、u（t）和y（t）分别为设定值、控制误差、控制输入信号和输出信号。

式中 τc1——期望的滤波器时间常数。

将式（4）中的e-θs用一阶泰勒公式逼近，近似为e-θs≈1-θs。 再由图1可知，当期望闭环传递函数为Cc1（s）并且已知时，考虑过程对象G（s）的模型是二阶时滞，则可得控制器C（s）为：

一般而言，τ应该大于系统延迟时间θ， 因为当τ<θ时，控制回路的响应会十分激烈甚至振荡；当τ过大时，系统的输出响应过程会变得迟缓。 综合考虑系统响应的快速性、 鲁棒性， 根据文献［8］，当τ=θ时，系统的性能最为理想。

2 模糊内模PID控制器设计

2.1 控制器介绍

模糊内模PID控制的主要思想是通过不同的规则得到不同的滤波器时间常数τ， 使得当过程模型参数发生变化时也能得到较为满意的控制效果。 其结构如图2所示。

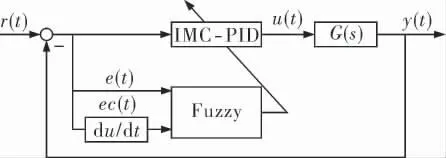
图2 模糊内模PID控制回路结构

图2中，IMC-PID是控制器，Fuzzy是模糊控制器，ec（t）是控制误差的变化率。

笔者建立二维的模糊控制器，分别以控制误差和控制误差的变化率作为输入，把模糊控制器输出当滤波器时间常数τ的变化， 从而实现对内模PID控制器参数的在线整定。

2.2 控制器设计

模糊控制器的输入是控制误差e（t）和误差的变化率ec（t），模糊控制器的输出u（t）则定义为滤波器的增量Δτ。 则实际的滤波器时间常数为：

式中 τ0——滤波器时间常数初值。

内模控制器的滤波器时间常数τ的选取决定了系统的鲁棒性和动态稳态特性，因此需要选定合适的值作为初始值，由前文可知，当τ=θ时，系统性能最好。 此时对应的PID参数分别为：

模糊控制器的输入e（t）、ec（t）和输出u（t）的语言变量分别表示为E、EC和U，它们相应的模糊子集如下：

隶属度函数是决定系统控制性能好坏的重要因素。 通常，如果在误差值比较小的情况下，就选择相对来说比较窄尖的隶属度函数；如果误差值比较大，那么就选择相对来说比较宽胖的隶属度函数。 笔者根据人为经验选取如图3所示的初始隶属度函数。

图3 e（t）、ec（t）、u（t）的隶属度函数

通过分析可知：τ越小， 系统响应速度越快，上升时间越短，但会造成超调量增大；如果τ取适中，被控对象的响应曲线稳定平缓上升，不会出现超调；如果τ过大，则控制器起主要作用的是比例控制， 过强的比例作用使得系统响应迟钝，上升时间大幅增加。 笔者根据人为经验选定表1所示的模糊规则表。

表1 模糊内模控制器初始模糊规则表

3 遗传算法优化模糊控制器

合理的规则表和隶属度函数能使系统达到较好的控制效果。 仅仅只优化前文所述的规则表，其解的空间高达55×5，这是一个非常庞大的数值。 显然传统的优化方法很难解决解空间太大的问题，需要找到一种能适用于解空间庞大问题的算法。遗传算法（GA）不失为一种优秀的解决此类问题的算法，它是Holland根据自然界中适者生存的法则和基因遗传的思想提出的一种优化算法。GA算法十分适用于复杂且解空间巨大的一类问题。 因此笔者选用GA算法作为寻优算法，对模糊控制器进行优化，寻优结构如图4所示。

图4 基于GA算法的模糊控制器寻优结构

3.1 遗传编码

利用遗传算法对模糊控制器进行整体优化，就是要同时考虑隶属度函数和规则表。 首先就是要将隶属度函数和规则表数字化，从简便、可操作性方面考虑，笔者直接使用十进制编码对隶属度函数和模糊控制规则表数字化。

由上文可知，笔者选取三角形为隶属度函数的形状，因此直接以三角形两个底边端点的坐标作为编码寻优对象。 以误差E为例：{NB（-1，an），NS（-1，an，0），ZO（an，0，ap），PS（0，ap，1），PB（ap，1）}，对语言变量误差变化率EC和控制量U也进行同样操作。 由以上分析可知，3个隶属度函数的待优化变量为6个，也就是3个三角形各自的底边端点，它们的编码表示为an、bn、cn、ap、bp、cp。

由上文可知， 笔者将模糊控制的效果分为5个等级， 因此首先选定5个整数来代表模糊语言的5个语言值（NB、NS、ZO、PS、PB）从而达到将模糊控制表数字化的先决条件。 表1所示的控制规则表， 其编码为 {55443 54434 44344 43445 34455}。

将上述两部分相加， 形成了最终的编码，该编码包括了模糊控制器的隶属度函数选取和规则表的制定，示意如下：

可以看出， 该编码串的前部分为规则表，由于笔者以二维控制器为例，因此规则共计5×5=25条，后部分为隶属度函数，共计6位编码，通过对以上共计31位编码的寻优就达到了对模糊控制器的优化。

3.2 适应度函数

适应度值表示种群个体的优劣程度，它是遗传算法进行的关键点。 在寻优过程中希望保存大量优秀的个体，快速淘汰劣质的个体，也就是适应度高的存活概率大， 适应度低的存活概率小。同时由实际经验得到，评估系统的性能应当充分考虑到动态特性和稳态特性， 也就是其响应时间、调节时间、超调量及误差等因素，因此需要找到一个满足上述要求的性能指标。 同时这个遗传算法要求个体适应度越大越好，所以笔者采用系统的累积绝对误差（IAE）作为性能指标，其表达式为：

宝胜党委狠抓“明责、履责、验责、问责”四个关键动作，通过实施党建“书记工程”项目，把党建工作的整体内容进行分解，细化任务，确定阶段目标，真正夯实基层党组织书记主体责任，推动基层党建工作真正落地到位。

3.3 遗传算子

在自然界中，生物的繁衍进化变异离不开基因的遗传，遗传算法很好地体现了这一点，遗传算法主要通过3种方式——选择、 交叉和变异来产生新的个体。

选择。 选择过程是模拟自然界适者生存的形式， 也就是个体按照他们的适应度繁衍的方式。其过程是，通过个体对环境的不同适应程度（由决定，其中n为种群规模，fi为群体中第i个个体的适应度）决定被复制个体。 因此适应度高的个体能够有较大的概率保存并繁衍下去。

交叉。 与选择不同，交叉不是将父代基因复制而是产生新个体的方式，它是通过某种结合的方式使两条染色体相互交换某些基因，以此形成新的染色体。 具体可表示如下：变异。 与交叉类似，它也是产生新个体的方式，与交叉不同的是它是在原有染色体的基础上畸变出原本没有的基因，形成新的染色体。 具体可表示如下：

通过变异提高遗传算法的局部搜索能力，同时维持群体的多样性，也就是充分满足解的多样性和全局性，防止出现部分收敛的现象。

3.4 算法操作步骤

基于遗传算法的模糊控制器寻优过程如下：

a. 确定遗传参数。 主要包括初始种群、迭代次数、染色体和变异概率。

b. 计算初始种群的适应度总值、平均值和最大值。

c. 选择。 根据达尔文的优胜劣汰法则，计算出每个个体的适应度值和平均适应度值的比值，若小于1则抛弃，反之则保留。

d. 交叉。 从父代染色体随机选取两条染色体，在随机位置进行染色体的交换。

e. 变异。产生0～1之间的随机数，每次比较随机数和设定的变异概率的大小，若随机数小于变异概率，则进行变异操作；若随机数大于变异概率，则跳过变异操作。

f. 判断是否满足终止条件。 若满足条件则停止迭代，不满足条件则继续迭代。

g. 在最终的染色体种群中选取适应度值最大的染色体，此时，将该染色体反编码就得到了最优的隶属度函数和规则表。

4 仿真实例

对于给定的传递函数：

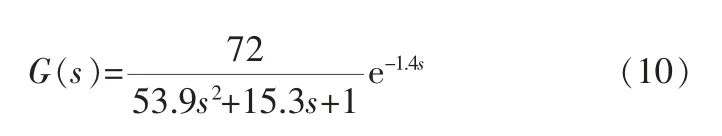
为验证笔者所提算法的有效性，利用上述过程对象进行仿真实验， 采用第3节所述模糊控制器对它进行控制，采用笔者所提算法对模糊控制器进行优化。

初始种群规模n=10，遗传代数P=40，采样时间T=0.35s，比例因子Ku=Ke=Kec=1。 分别记录迭代10、20、30次的实验结果，其中仿真时间为200s，所有的适应度值见表2。

表2 适应度值

由表2可以看出，随着迭代次数的增加，适应度呈递增状态。 这说明，在经过30次迭代后取得了较满意的控制效果。

初始状态（未进行优化操作）和进化到第10、20、30代时的阶跃响应曲线如图5所示。

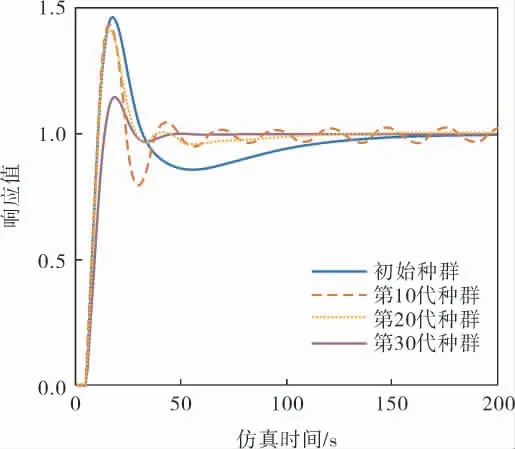
图5 不同迭代次数时系统的响应曲线

由图5可知，采用笔者所述算法优化后，系统的控制效果得到明显提升，超调量明显下降，上升时间也减少， 由计算可得系统IAE值也大幅减小。优化后的隶属度函数如图6～8所示，规则见表3。

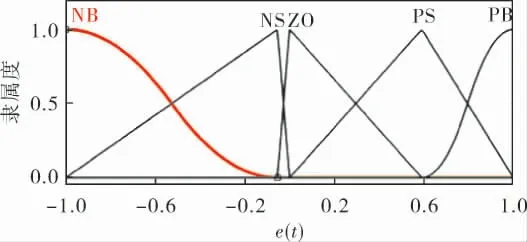
图6 优化后e（t）的隶属度函数

图7 优化后ec（t）的隶属度函数

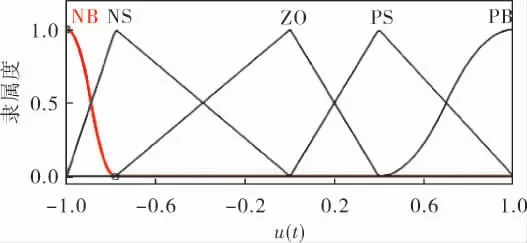
图8 优化后u（t）的隶属度函数

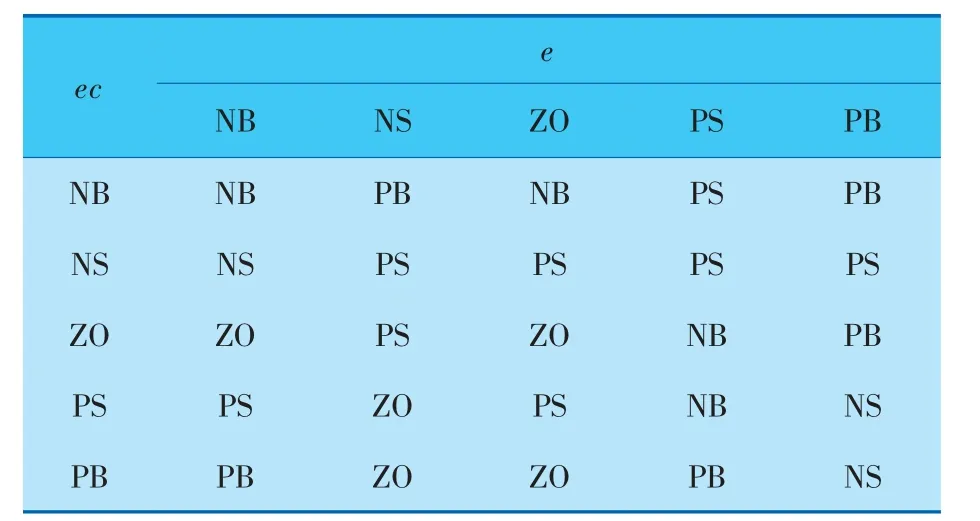
表3 最优模糊规则表

5 结束语

为了摆脱人为经验对模糊规则和隶属度函数确定的局限性，笔者提出了一种基于遗传算法的模糊内模PID控制寻优算法， 在缺乏甚至没有人为经验时也能够找到最优的模糊规则表和相应的隶属度函数。 同时，结合模糊控制与内模控制的优化，在线整定系统滤波器参数，可使系统控制效果兼顾动态性、稳态性和鲁棒性。