基于改进差分进化算法的机器人动力学参数辨识方法研究
2020-08-17张建宇段建龙
张建宇 段建龙


[摘要]针对传统差分进化算法存在收敛精度不高和算法容易陷入局部最优等问题,提出一种差分进化(Differential Evolution, DE)算法的改进方案,并用于机器人的动力学参数辨识。首先,利用Newton-Euler方法建立含有关节摩擦特性的机器人动力学模型的线性形式,设计严格满足机器人运动条件的傅里叶级数作为运动轨迹,为提高辨识精度,建立机器人观测矩阵条件数的非线性约束模型来优化激励轨迹;其次,引入DE算法并对其进行优化以提高算法的全局搜索能力和开发能力;最后,以智昌川崎RSOION机器人为对象设计仿真实验,实现了机器人动力学参数的辫识,并对辫识结果与理论值进行了对比分析。结果表明,采用改进的差分进化算法,可以准确地辨识出机器人动力学参数,所建立的模型能够反映机器人的动力学特性。
[关键词]参数辨识;差分进化算法;Newton-Euler法;动力学参数
[中图分类号]TP242 [文献标志码]A [文章编号]1005-0310(2020)01-0048-09
0 引言
20世纪以来科学技术的迅速发展致使越来越多的科学家投人到机器人的研究与开发当中。早期的机器人因软硬件方面的不足,导致人们在进行机器人控制时主要采用控制律简单、不考虑动力学特性的“运动控制”方法。此方法控制精度较低,适用于对机器人精度要求不高的场合,但在控制高速、高精度机器人方面有两个明显的缺点:一是难以保证受控机器人具有良好的动态和静态品质;二是需要较大的控制能量[1]。为满足现今机器人复杂而高精度的动作要求,大部分机器人的控制器都采用具有良好动态和静态品质的“动态控制”方法,此方法利用机器人的动力学特性设计更加精细的非线性控制律来实现机器人运动控制[2]。因此,能够准确辨识机器人的动力学参数,得到精确的机器人动力学模型,对实现机器人精确控制起着至关重要的作用。
机器人的动力学参数辨识过程包括5个步骤:动力学建模、激励轨迹设计、数据采样和滤波处理、参数辨识和模型验证。丁亚东等采用分步辨识的方法大大降低了辨识难度[3];Azeddien Kinsheel等提出一种基于最小二乘法的参数辨识方法,但因其计算量大、实时性差很难得到采用[4];Renders等提出一种逐步辨识机器人机械臂的质量、质心、惯性张量的方法,但辨识出的机器人动力学参数可靠性不高[5];丁力等提出一种用遗传算法对模型进行参数辨识的方法,但其算法本身编码过程烦琐,辨识效率不高[6];Poli R等提出的粒子群优化算法虽然简单,但由于搜索空间有限,不能保证其达到全局最优[7]。
差分进化(Differential Evolution,DE)算法于1995年被Rainer Storn和Kenneth Price提出,是一种模拟自然界种群的以“优胜劣汰,适者生存”为进化规律的搜索算法,具有简单易用以及很强的全局收敛能力,目前已用于多个领域。现有研究表明,该算法在处理多维、非线性的复杂函数方面明显优于遗传算法、粒子群算法等智能算法,已成为各行业不可或缺的解决复杂问题的方法[8]。
为提高机器人参数辨识精度,本文提出一种基于改进差分进化算法的参数辨识方法,该方法可以动态跟踪算法当前的搜索情况,以调整其搜索策略,增强搜索能力,提高收敛速度。通过使用智昌川崎RSO1ON机器人模型设计仿真实验,验证了辨识算法的正确性和有效性。
1 机器人动力学模型
使用Euler-Lagrange方程和Newton-Euler方程都可以建立自由运动机器人动力学方程,但后一种方法常用于数值计算,而且方程具有递推形式,其计算量比前一种要少得多,因此本文用Newton-Euler方程递推得到n自由度机器人动力学方程[9]:式中:τdyn是n×1的关节力矩向量;D(q)是n×n的惯性矩阵;C(q)是n×n的离心力和科里奥利向量;G(q)是n×1的重力向量;q、q、q分别表示n×1的位置向量、角速度向量和角加速度向量。
由式(1)可知机器人的动力学方程是通过连杆质量、惯性张量等参数进行定义的,要建立动力学模型就必须要确定这些参数。但动力学方程是个非线性方程,要確定这些参数比较困难,幸运的是机器人动力学方程在惯性参数方面是线性化的,存
但是,由于机器人各关节在运动过程中相互耦合以及机械臂的运动受到约束,实际上只有部分动力学参数影响机器人的运动状态,即实际相互独立的机器人动力学参数少于10n个,这使得在用包含全部机器人动力学参数的方程作参数辨识时,得到的动力学参数是不准确的。因此,寻找一个最小惯性参数集用来替代惯性参数向量从而简化动力学方程就显得尤为重要。文献[11]根据惯性参数重组法得到了用最小惯性参数表示的动力学方程:
由方程(4)得到的包含最小惯性参数的动力学方程适用于动力学仿真,但并不适用于现实中的机器人,因为机器人在实际运动过程中还存在摩擦力做功的现象,并且电机转子在运动过程中产生的转动惯量也需要消耗电机力矩。其中,转动惯量在机器人出厂前已知,在建模时将其补偿到力矩方程即可。因此,实际模型中只需考虑摩擦力的问题,机械臂摩擦模型是个非常复杂的非线性模型,很难进行精确建模。目前比较常见的摩擦模型有Dahl模型、Stribeck模型和库伦粘滞模型。综合考虑辨识过程的复杂度、辨识精度等因素,本文选取只包含库伦摩擦参数和粘滞摩擦参数的库伦粘滞摩擦模型(12),即
由此可知,机器人刚体动力学力矩和机器人摩擦力矩的可辨识参数仅与机器人角位移、角速度和角加速度有关。故由式(4)和式(5)可知机器人动力学模型为
2 激励轨迹的设计及优化
为使参数辨识的精度不会因机器人建模误差、环境噪声等因素而受到影响,需要精心设计激励轨迹。考虑到抗干扰能力、机器人的运动约束等因素,本文选取数据处理方便、对干扰不灵敏、对机器人速度和加速度有良好约束的傅里叶级数作为激
将激励轨迹导入到机器人进行参数辨识时,由于机器人自身各关节位置、角速度、角加速度极限值的限制,导致无法准确获得部分的机械臂动力学参数,直接影响参数辨识的精度。为使辨识过程中能够准确估计动力学参数,需要对激励轨迹进行优化。目前激励轨迹的优化方法有协方差矩阵法、神经网络、遗传算法等多种优化方法,但大多数方法都以动力学方程中观测矩阵的条件数cond(Y)为优化目标。本文通过建立基于条件数的非线性约束模型来优化激励轨迹。基于条件数的非线性约束模型可表述为
3 改进差分进化算法
差分进化算法在处理多维、非线性的复杂函数方面明显优于遗传算法、粒子群算法等智能算法,已成为各行业不可或缺的解决复杂问题的方法。本文在传统差分进化算法的基础上对其进行优化,并验证了改进算法的收敛性和全局搜索能力。
3.1 标准差分进化算法
差分进化算法是基于群体智能理论的优化算法,采用群体的全局搜索策略,其基本结构与遗传算法类似,主要包括变异、交叉和选择3个部分。其基本思想由随机产生的初始群体开始,通过变异和选择操作产生新个体,然后通过比较新个体与此代中个体的适应度值,淘汰劣质个体,经过不断的迭代进化使个体趋向于最优解。标准差分进化算法主要包括以下4个步骤。
3.1.1 生成初始群体
3.1.2 变异操作
变异策略为DE算法的核心部分,对目标个体进行扰动来产生变异个体。在DE算法中目前广泛使用的变异策略有两种:
3.1.3 交叉操作
交叉操作是为了增加群体的多样性,具体操作为
在满足终止条件之前,反复执行变异操作和选择操作。
3.2 改进差分进化算法
差分进化算法通过群体中个体间的合作和竞争产生的群体智能来引导群体进化。但是,由于种群间个体聚集,个体间相似度较高,导致算法在运行过程中易陷入局部最优、收敛速度较低的状态[14]。针对该算法的不足之处,借助以往学者对DE算法的研究,本文对算法进行了以下的改进。
3.2.1 变异策略的改进
差分进化算法是全局搜索算法,因此在算法搜索初期需要尽可能多地在群体间进行搜索,保证种群的多样性,在算法后期应快速找寻最优个体,加快种群收敛速度。变异策略作为算法的核心部分,其变异向量的构造形式直接关系到算法的寻优效果。但常用的DE算法的变异策略如DE/rand/1/bin、DE/best/2/bin致使算法在不同时期具备不同的搜索能力和开发能力。针对此种情况,本文提出了一种双策略变异算子,此变异算子可使DE算法在前期具备较强的搜索能力,在后期具备较强的收敛能力。变异算子的表达式为
3.2.2 交叉策略的改进
交叉策略根据交叉因子决定遗传给下一代的个体。Islam[15]为了提高算法的收敛精度,采用一种线性递减机制,用当代种群中随机选取的个体代替父代个体。本文参照此方法,并使用文献[16]提出的中心粒子群優化算法中的当代中心解取代父代个体。交叉策略优化方法为
3.2.3 参数的自适应调整
变异因子F和交叉因子CR可控制算法的种群多样性,平衡局部与全局搜索能力。变异因子F的取值较大时,群体间差异度较大,算法易跳出局部极值但会减慢算法的收敛速度;当变异因子F的取值较小时,算法因群体差异较小导致其不易跳出局部最优。交叉因子CR过小会减小种群多样性,使群体中的个体过早收敛;CR过大会提高算法收敛
3.3 改进算法性能测试
为测试改进差分进化算法的收敛能力和全局搜索能力,采用3个常用的测试函数用以验证,并与其他优化算法的测试结果进行比对。测试函数如表1所示。
表1所示的测试函数中,f1(x)只存在全局最优解,因此该函数可以很好地测试算法的收敛速度;其他测试函数存在较多的局部最优点,可以较好地测试算法的全局搜索能力。在算法参数设置中,种群规模M取为100,最大迭代次数R取为500,变异因子最大值和最小值分别取Fmax=0.6、Fmin=0.3,交叉因子最大值和最小值分别取CRmax=0.9、CRmin=0.6,维数D=30。表2和表3分别给出了3种算法对测试函数的寻优结果和迭代次数。
表2的寻优结果证实改进DE算法不易陷入局部最优,全局搜索能力强;表3的数据表明,改进DE算法的收敛能力明显高于其他优化算法。
4 参数辨识结果分析
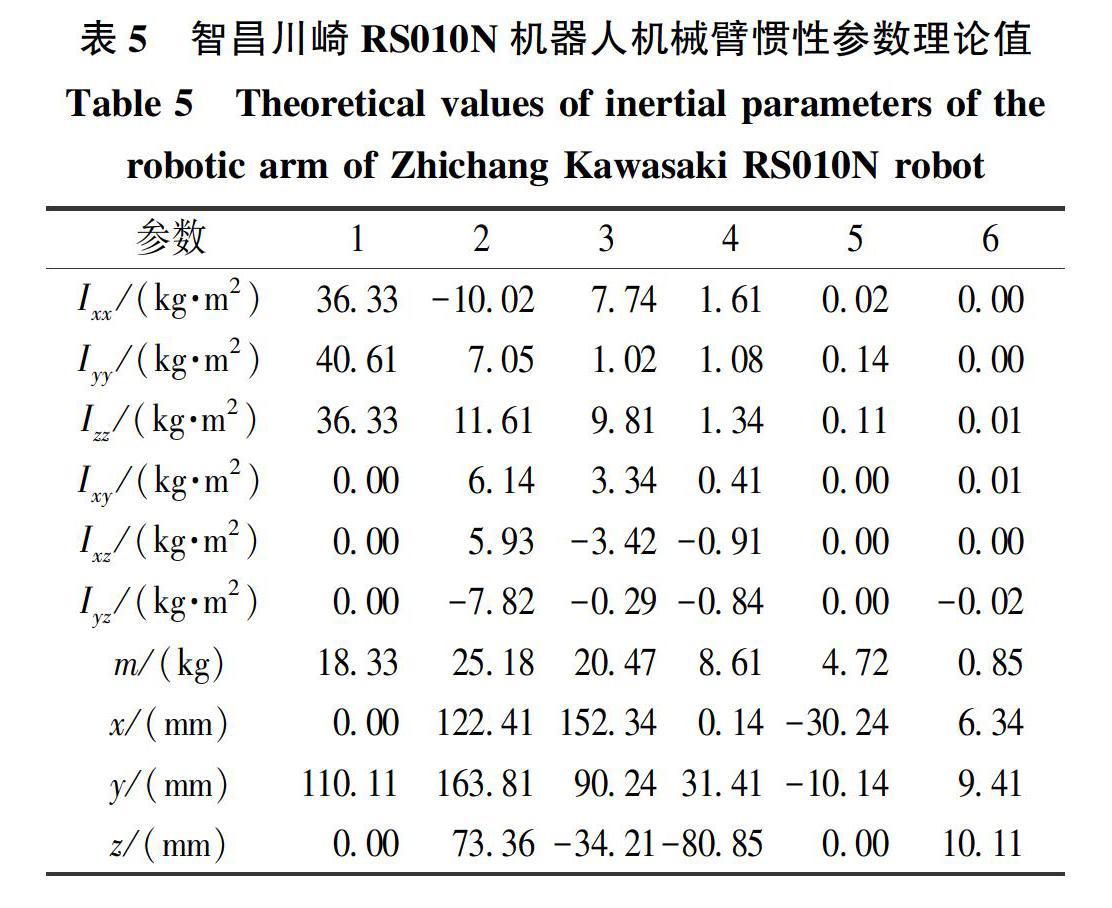
机器人的参数辨识过程极其复杂,本文以智昌川崎RSOION机器人进行了仿真实验,机器人实体如图1所示。图2是其坐标系配置。表4给出了DH参数(杆件长度ai定义为从Zi-1轴到Zi轴的距离,沿Xi轴的指向为正;杆件扭角αi定义为从Zi-1轴到Zi轴的转角,绕Xi轴正向转动为正,且规定αi∈(-π,π];关节距离di定义为从Xi-1轴到Zi轴的距离,沿Zi-1,轴的指向为正;关节转角θi定义为从Xi-1轴到Zi轴的转角,绕Zi-1轴正向转动为正,且规定θi∈(-π,π]。表5给出了机械臂惯性参数理论值。由于典型6自由度工业机械臂的肘关节和腕关节惯性参数的差异性,前3个关节的动力学参数远远大于后3个关节,因此在参数辨识时忽略后3个关节力矩的影响,只辨识前3个关节的动力学参数。
辨识过程分以下几个过程完成:首先,建立智昌川崎RSOION机器人模型并将其线性化,此辨识试验只以仿真的形式进行,故在建模时不需要考虑摩擦力的影响;其次,以动力学方程中观测矩阵的条件数为优化目标设计激励轨迹,使机器人沿激励轨迹运动;最后,采集机器人在一个运动周期内的各关节力矩数据并将其代入优化算法,便可得到机器人的动力学参数。
按表6所示的机械臂前3个关节运动学约束条件优化激励轨迹,其基频为ωf=0.1Hz(周期为10s),谐波项数目D=5,优化得到激励轨迹如图3所示。由表4、表5给出的机器人DH参数和惯性参数,在Matlab/Simulink中建立智昌川崎RS010N机器人模型,图4为模型的一部分。固定机器人4、5、6关节,并将图3所示的激励轨迹导入机器人模型,在一个运动周期内各关节所受力矩情况如图5所示。
将关節的实际测量数据导入差分进化算法中可得到机器人前3个关节的动力学参数,具体参数辨识流程如图6所示。在参数辨识算法中,个体是通过相互比较其适应度值来选择进化方向的,本文定义个体xjk的适应度函数fit(xjk)为式中:N为采样数据的个数;n为机器人的关节数;τiμ为关节i的实际采样力矩;τpiμ为关节i的预测力矩;ki∈(0,1)为机器人关节i的权重系数,其值可由出厂值获得。算法迭代搜索的目标是使适应度函数达到最小,搜索空间可根据机器人出厂数据进行设定。
因机器人前三轴的动力学待辨识参数为21个,故改进差分进化算法中个体维度为21,根据机器人的出厂数据情况分析,机械臂的动力学参数一般在-200~500之间取值,种群规模M取为100,最大迭代次数K取为100,变异因子最大值和最小值分别取Fmax=0.6,Fmin=0.3,交叉因子最大值和最小值分别取CRmax=0.9、CRmin=0.6。本算法从某一随机产生的初始群体开始,通过个体不断迭代进化并最终趋向于最优解。图7为适应度函数的优化过程,由图可以发现,随着迭代次数的增加,适应度函数值逐渐降低,并且到第40代时适应度函数值基本趋向稳定,由此可以断定个体在进化过程中,没有陷入局部最优,通过比较适应度函数值进化得到的最优个体,即为机器人的动力学待辨识参数。表7所示为机器人1、2、3关节动力学参数的理论值和辨识值。
表7对机器人动力学参数的理论值与辨识值进行了对比,发现其每个参数的绝对误差均非常小,表明本文方法可准确地辨识出机器人动力学参数。
5 结论
本文针对n-连杆机器人的动力学参数辨识问题,提出了一种基于改进差分进化算法的动力学参数辨识新方法。该算法在传统差分进化算法基础上优化了变异策略和交叉策略的构造形式,从而提高算法的全局搜索能力和开发能力;设计满足动力学约束条件的激励轨迹,通过改进差分算法实现了机器人的动力学参数辨识,并将辨识结果与理论值进行了对比。结果表明,文中优化算法具备较强的全局收敛能力和寻优能力、较高的辨识精度,能够实现对机器人动力学参数的精确预测。
[参考文献]
[1]WU J,WANG J,YOU Z.An overview of dynamic parameter identification of robots[J].Robotics and Computer-IntegratedManufacturing,2010,26(5):414-419.
[2]YOUNG K,PICKIN C G.Accuracy assessment of the modern industrial robot[J].Industrial Robot:An InternationalJournal,2000,27(6):427-436.
[3]丁亚东,陈柏,吴洪涛,等一种工业机器人动力学参数的辨识方法[J].华南理工大学学报(自然科学版),2015,43(3):49-56.
[4]AZEDDIEN K.Robust least square estimation of the CRS A465 robot arms dynamic model parameters[J].Journal ofMechanical Engineering Research,2012,4(3):911-1004.
[5]RENDERS J M,ROSSIGNOL E,BECQ.UET M,et al.Kinematic calibration and geometrical parameter identification forrobots[J].IEEE Transactions on Robotics and Automation,1991,7(6):721-732.
[6]丁力,吴洪涛,姚裕,等.基于WLS-ABC算法的工业机器人参数辨识[J].华南理工大学学报(自然科学版),2016,44(5):90-95.
[7]POLI R,KENNEDY),BLACKWELL T.Particle swarm optimization:an overview[J].Swarm Intelligence,2007,1(1):33-57
[8]STORN R,PRICE K.Differential evolution,a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization,1997,11(4):34-59.
[9]HOLLERBACH J M.A recursive lagrangian formulation of manipulator dynamics and a comparative study of dynamicsformulation complexity[J].IEEE Transactions on Systems,Man,and Cybernetics,1980,10(11):730-736.
[10]VANDANJON P O,GAUTIER M,DESBATS P.Identification of robots inertial parameters by means of spectrum analysis[C]//IEEE International Conference on Robotics and Automation.IEEE,1995,2(8):3033-3038.
[11]GAUTIER M,KHALIL W.On the identification of the inertial parameters of robots[C]// IEEE Conference on Decision andControl.IEEE,1988,7(2):2260-2269.
[12]GROTJAHN M,DAEMI M,HEIMANN B.Friction and rigid body identification of robot dynamics[J].International Journalof Solids and Structures,2001,5(1):1889-1902.
[13]SWEVERS J,GANSEMAN C,SCHUTTER J D, et al.Experimental robot identification using optimised periodic trajectories[J].Mechanical Systems and Signal Processing,1996,10(5):561-577.
[14]MIAO Q,ZHU R.A Monte Carlo localization method based on differential evolution optimization applied into economicforecasting in mobile wireless sensor networks[J].EURASIP Journal on Wireless Communications and Networking,2018,2(1):638-658.
[15]ISLAM S M,DAS S,GHOSH S,et al.An adaptive differential evolution algorithm with novel mutation and crossoverstrategies for global numerical optimization[J].IEEE Transactions on Systems, Man and Cybernetics,Part B(Cybernetics),2012,42(2):482-500.
[16]LIU Y,QIN Z,SHI Z W,et al.Center particle swarm optimization[J].Neurocomputing,2007,70(4-6):672-679.
[17]DAS S,KONAR A.Two improved differential evolution schemes for faster global search[C]//Proceedings of the GeneticEvolutionary Computation.Washington DC,USA,2005:991.
(責任编辑 白丽媛)[收稿日期]2019-07-01
[基金项目]国家自然科学基金项目(51675009)。
[作者简介]张建宇(1975-),男,北京市人,北京工业大学机电学院副教授,主要研究方向为机械系统动力学仿真;段建龙(1993-),男,甘肃定西人,北京工业大学机电学院硕士研究生,主要研究方向为工业机器人轨迹规划。E-mail:zhjy_1999@bjut.edu.cn
