翼型凹变在风电叶片气动性能优化中的应用研究
2020-08-17唐格斯董雅君霍德豪马剑龙
唐格斯, 陈 建, 董雅君, 霍德豪, 赵 爽, 马剑龙,4
(1. 内蒙古工业大学 电力学院, 内蒙古 呼和浩特 010080; 2. 营口市钢铁和镁产业基地建设发展中心, 辽宁营口 115000; 3.内蒙古工业大学 能源与动力工程学院, 内蒙古 呼和浩特 010051; 4.内蒙古自治区高等学校可再生能源工程研究中心, 内蒙古 呼和浩特 010051)
0 引言
随着风电机组设计的日益大型化以及其分散式应用向人类生存环境的靠近,对人类生存环境的影响越来越大,叶面流动分离恶化问题已成为叶片气动性能设计成败的关键制约[1]。因此,寻找并建立基于叶面流动分离有效控制的叶片气动性能优化方法,已成为当前风电产业发展中亟待解决的重要课题。 翼型向翼面内侧的结构凹曲变形(以下简称翼型凹变)作为防止和推迟流动分离发生的重要方法,近年来已成功应用于飞机机翼气动性能的优化设计[2],[3]。 然而,风电叶片结构较飞机机翼更为复杂,由此导致气体绕流风电叶片时的非定常流动特征要比绕流机翼时复杂得多,因此,直接将相关成果应用于风电叶片气动性能的优化设计不具备可靠性。 由此,相关研究工作的开展具有较好的背景和价值。
翼型凹变在风电叶片气动性能优化中的应用属于全新的课题,但是,翼型凹变属于翼型优化设计范畴。 基于翼型优化的叶片气动性能研究主要包括风电叶片专用翼型开发和先进设计方法开发两个方面。 早期的叶片设计普遍采用航空翼型(如NACA 系列翼型),航空翼型具有最大升力系数高、最小阻力系数低等优点,对风电产业的早期发展起到了极大的推进作用。 然而,后续诸多实践证实航空翼型对于高气动性能风电叶片设计的适用性存在较多缺陷, 亟待风电叶片专用翼型的研发。自20 世纪80 年代中期开始,风电专用翼型的开发得到重视。至今,已形成了美国S 系列、荷兰DU 系列、瑞典FFA-W 系列和丹麦Risφ系列翼型,为大、中、小型风电叶片的设计提供了基础翼型数据[4]~[7]。 此外,研究人员还专门针对大型风电叶片开发了WQ-B 系列翼型[8]。
20 世纪末, 小型风电叶片的应用陡然升温,相应专用翼型的开发也逐渐增多, 此时的研究工作不仅着力于专用翼型的开发, 同时特别关注叶片低速启动问题和失速问题[9]~[11]。自2010 年起,建筑用风力机的开发得到重视, 至今已有多款专用翼型问世[12]。 随着专用翼型的丰富,新翼型研发所需的长研发周期和高昂的研发费用使开发企业望而却步。 因此,20 世纪末起至今,针对于已有翼型的气动性能优化设计方法受到青睐, 期间风电市场的极速扩张和投资商不愿在技术引入费上的过多投入, 更是在极大程度上推动了相关问题的研究。 这一时期,研究人员不仅关注反设计法、失速延迟法、 遗传算法等先进算法在翼型气动性能优化中的应用, 同时对叶面的流动分离控制技术给予了特别的关注[13]~[16]。 国内外的相关研究人员分别在叶面流动分离的控制问题上开展了基础性研究[17]。 但至今,除作者课题组外[18],仍未见基于翼型凹变的叶片气动性能优化方面的报道。
1 翼型凹变想法提出的理论基础
图1 为空气绕流翼型时的流动特征。
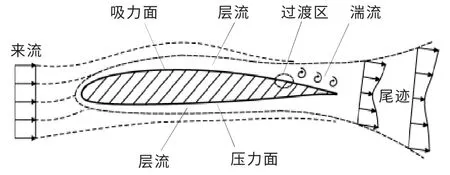
图1 空气绕流翼型时的流动特征Fig.1 Flow characteristics of air around airfoil
由图1 可知,当空气流经翼型表面时,在吸力面上靠近尾缘处往往存在由层流向紊流转变的流动分离区。由流体力学基础理论可知,层流边界层在物体表面上产生的切向应力比紊流的要小得多,为了减小流动摩擦阻力,应使层流边界层尽可能地长, 也就是使流动分离位置尽可能向下游推移,从而提升叶片的功率输出。
加速流动比减速流动更容易使边界层保持层流,为了实现流动分离点向下游的移动,本文尝试在流动分离区域附近实现翼型向翼型面内侧的结构凹变, 利用凹槽的抽吸作用使已经减速的流体得以加速, 从而防止或延后流动分离现象的发生。
2 翼型凹变形式的确定
图2 为翼型凹变的实现过程。

图2 翼型凹变的实现过程Fig.2 Implementation process of airfoil concave
以图2(a)中翼型为例,假设流动分离常出现在M 处,则选该处为凹变中心。 考虑到翼型弦长显著大于其最大厚度, 翼型凹变的几何结构采用椭圆形,椭圆的长轴(A)为弦长(L)的7.2%、短轴(B)为弦长(L)的3.6%,并使A 与M 处原始翼型曲线相切, 本例中相切后A 与弦长间的夹角(α)为2.25°。凹变部分与非凹变部分间采用B 样条曲线连接,具体过程如图2(b)所示。
原始翼型叶片的结构如图3(a)所示。 叶片为实心结构,长为700 mm,设有10 个特征翼型面,每个特征翼型面之间的叶片部分通过放样实现,将原始翼型中的10 个特征翼型曲线执行相应的结构凹变, 并对各翼型曲线进行放样后即可生成凹变翼型叶片[图3(b)]。

图3 叶片的生成Fig.3 Blade generation
3 翼型凹变位置和凹槽长度的确定
3.1 凹变位置和凹槽长度的预选
翼型凹变的中心尝试选取在距离翼型前缘点0.7 倍、0.8 倍和0.9 倍L 处,凹槽的长度(由叶根指向叶尖)尝试选取为350,420,700 mm,叶片代号及相应结构形式见表1。 翼型凹变位置和凹槽长度的最终选定需以叶片做功能力的大小为参考。
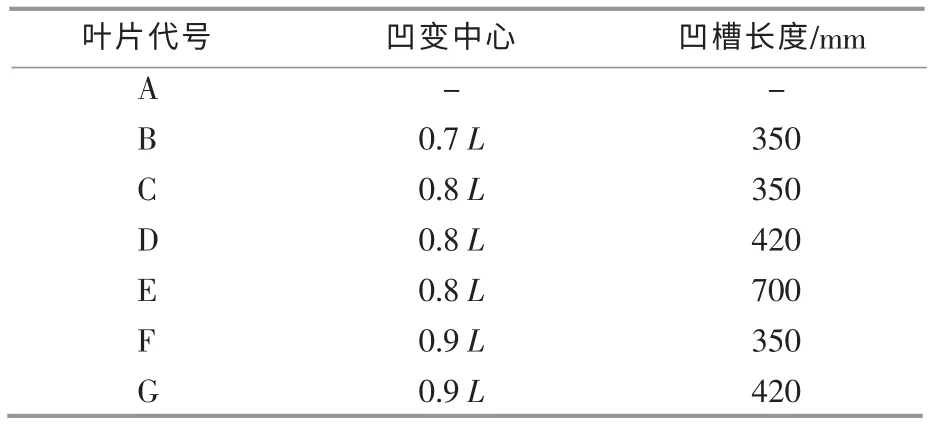
表1 叶片类型Table 1 Types of blades
3.2 计算模型
计算模型如图4 所示。 该数学模型是依据内蒙古自治区新能源试验示范基地的B1/K2 型低速风洞建立, 目的是利用相应的实验数据检验数值仿真结果的可靠性。
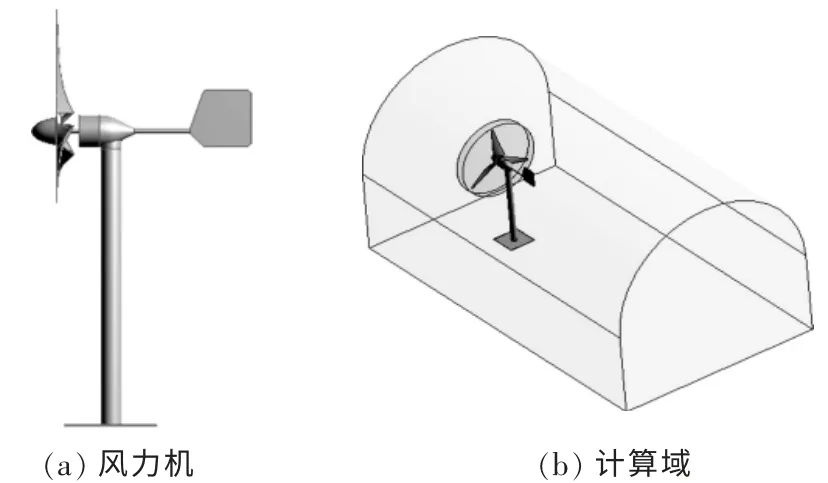
图4 数值仿真模型Fig.4 Numerical simulation model
3.3 网格划分
3.3.1 流场网格划分
网格分为静止域和旋转域, 交界面间数据传递通过滑移网格实现,其控制方程如式(1)所示。
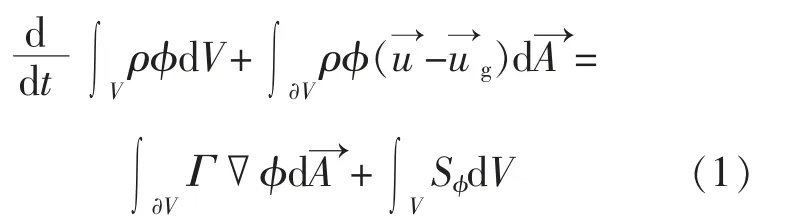
图5 所示为计算域采用分区域加密。
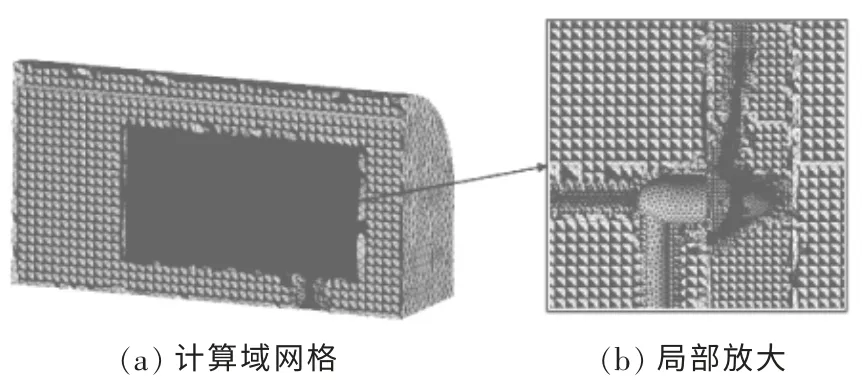
图5 网格的分区加密Fig.5 Partition encryption of mesh
3.3.2 结构场网格划分
由于风力机叶片包含较多曲面, 叶片扭角较大的位置对网格划分质量要求较高, 所以对叶片较薄处区域利用贴体网格进行加密。 计算域入口以速度作为边界条件(选择额定风速为8 m/s),出口以静压作为边界条件(相对压力设为0 Pa)。
计算域的壁面及地面设置为无滑移壁面,壁面的粗糙度为光滑壁面。 风力机的壁面设置为无滑移壁面,壁面粗糙度为光滑壁面。依据风力机实际测试条件,流体材料设为25 ℃的空气,并为连续流体。
3.4 湍流模型及控制方程
3.4.1 湍流模型
由于所选算法须考虑湍流剪切应力, 且不会对湍流黏度产生过度预测, 同时考虑到计算的时间成本,因此,本文选用SST k-ω 模型开展计算。
3.4.2 控制方程
控制方程为
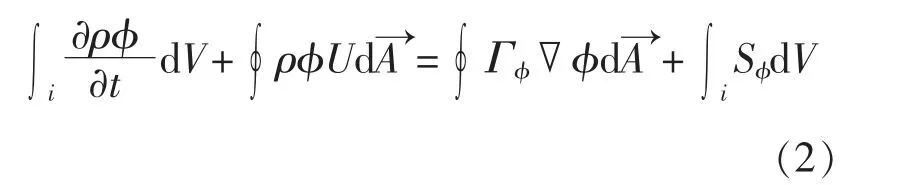
计算域中网格的每一个单元都是一个独立控制体,式(2)能够运用于每一个单元,这样控制体方程可以表达为
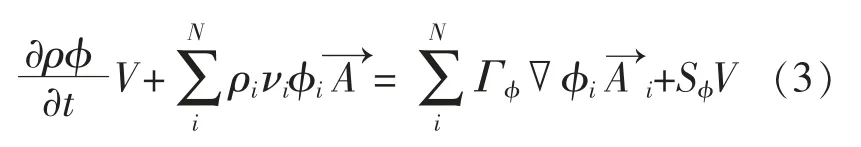
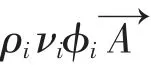
3.5 计算结果
在非稳态条件下利用SST k-w 算法开展计算。 以来流风速为8 m/s、叶尖速比为5 为例,7 类叶片气动性能的数值计算结果如表2 所示。 由表2 可知,6 种翼型结构的凹变形式中,C 叶片的功率输出提升效果更为显著。 因此,以下开展C 叶片和A 叶片其它方面性能的对比。
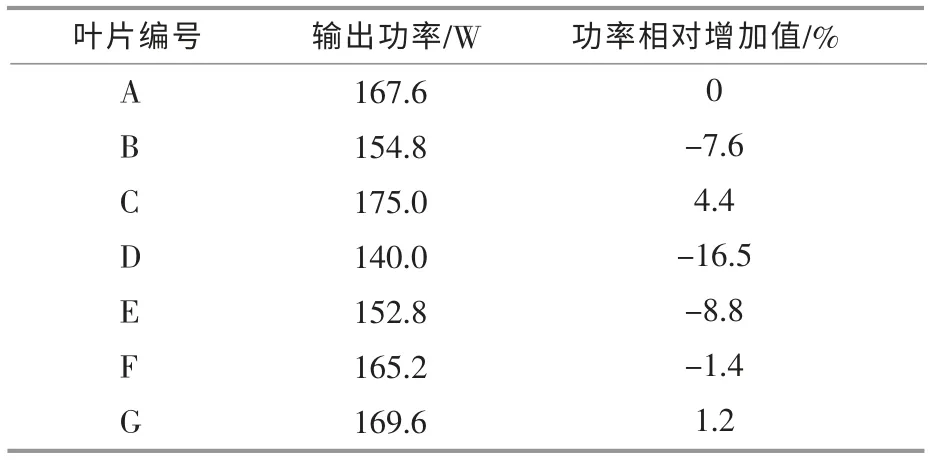
表2 不同凹变形式对叶片输出功率的影响Table 2 Influence of different concave types on blade power output
4 翼型凹变对叶片气动性能的影响
加工制作的A 类和C 类叶片如图6(a)所示,测试风洞如图6(b)所示。 风洞开口实验段内径为2 m,可提供0~20 m/s 的均匀来流。 发电机输出信号由Fluke Norma5000 装置采集, 其可实现电频率、电压、电流、电功率等多种发电机输出参数的实时监测。 叶片的转速可通过发电机输出电频率除以电极数间接获得。

图6 叶片和测试设备Fig.6 Blade and test device
4.1 测试结果与分析
为了考证不同工况时翼型凹变对叶片气动性能改良的适应性, 分别在来流风速为5~8 m/s 和叶片转速为400~650 r/min 时开展测试,结果如图7 所示。由图7 可知:翼型凹变对叶片气动性能的提升效果不仅仅适用于额定工况,在其它工况时也有较理想的提升效果; 在来流风速为8 m/s、叶尖速比为5(对应叶片转速为550 r/min)时,A,C叶片功率输出的数值仿真结果相对于实验值的相对误差分别为6.2%和6.4%, 由此也证实了上述仿真结果的可靠性。 仿真值大于实验值的原因为数值仿真为理想工况,没有考虑叶片实际运行中的流动损失。

图7 翼型结构凹变对叶片气动性能的提升Fig.7 Effect of airfoil concave on the aerodynamic performance of blades
为进一步量化翼型凹变对叶片气动性能影响的敏感性, 对同一工况时功率的增幅φp做如下定义:

式中:P1为原始翼型叶片功率;P2为凹变翼型叶片功率。
凹变对叶片气动性能影响的敏感性如图8所示。 由图8 可知:当风速为7 m/s 时,翼型凹变对叶片气动性能的增益最小;当风速为6 m/s 和8 m/s 时,增益值会有一定程度的增加;当风速为5 m/s 时,随着叶片转速的增加,翼型凹变对叶片气动性能的增益效果会显著增加;当风速为7 m/s和8 m/s 时,随着叶片转速的增大,由于翼型凹变导致的叶片气动性能的增加量呈先减小后增大的规律;当来流风速为5 m/s 和6 m/s 时,增益值随着叶片转速的增大而增大。
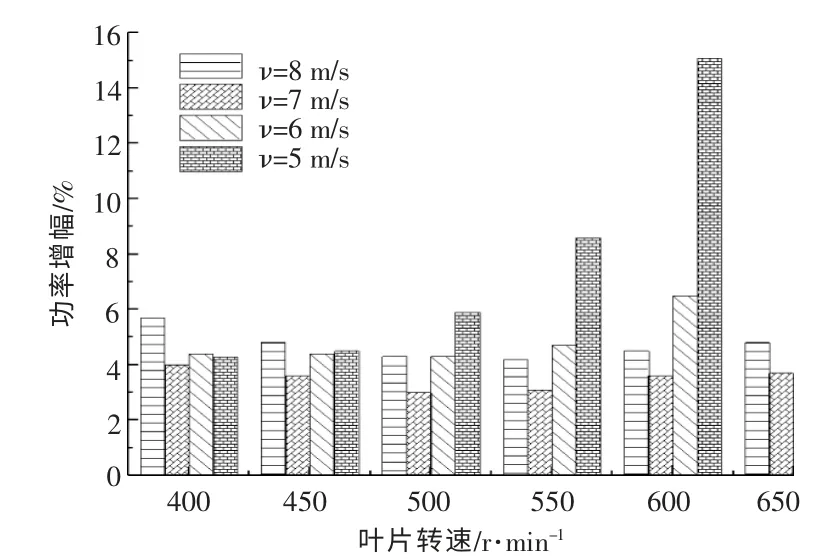
图8 凹变对叶片气动性能影响的敏感性Fig.8 Influencing sensitivity of the airfoil concave to the aerodynamic performance of blades
4.2 翼型凹变对叶片气动性能影响的机理分析
为进一步探究翼型凹变对叶面流动影响的机理。 令叶片长度为R,考虑到C 叶片的凹槽分布于叶片叶展方向的0.15R~0.65 R(以叶根为起点)的范围内, 将翼型面压力分布的提取位置设在0.3R,0.4R,0.5R,0.6R 处(图9),图中1,2,3,4 截面分别对应上述4 个位置。

图9 压力数据的提取截面Fig.9 Extraction section of pressure data
仍以来流风速为8 m/s, 叶尖速比为5 为例,1~4 截面上的压力分布如图10 所示,图中左侧为原始翼型叶片,右侧为凹变翼型叶片。
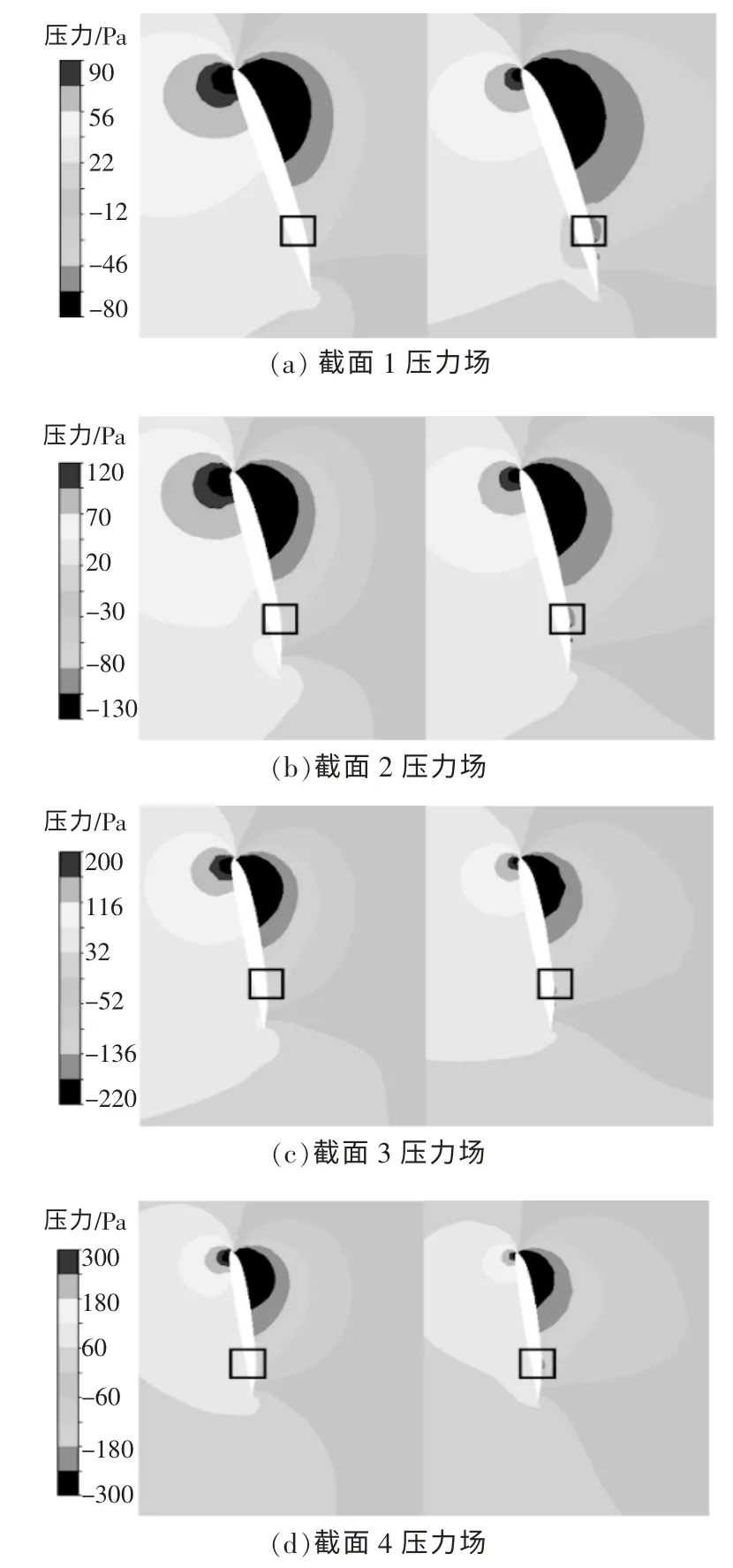
图10 叶片不同位置处的压力分布Fig.10 Pressure distribution at different locations of the blade
由图10 可知:在A 叶片的0.8 倍弦长区域附近,确实存在明显的压力升高现象,不利于层流流动的保持;凹槽的出现会使附近压力明显降低,进而对流体流动产生明显的局部压力诱导效应,使流体产生加速流动。
由流体力学基本理论可知, 加速流动比减速流动更容易保持层流的流动状态, 可使层流流动向紊流流动过渡的位置向后推移, 有效减小流态转变诱发的流动阻力增加, 从而使叶片的气动性能提升,这也是相同工况下C 叶片的功率输出较A 叶片提升的原因。
5 结论
本文利用椭圆弧在叶片吸力面上实施了翼型凹变,通过凹变参数的合理选择,可以实现对叶面流动分离的有益控制。就本文凹变样例而言,可以得出以下结论。
①翼型凹变在不同工况(不同风速和叶片转速)下对叶片做功能力的增益效果存在明显差异。
②启动风速至额定风速间, 翼型凹变对某一中间风速下叶片做功能力的增益效果最差。
③低风速时,随着叶片转速的增大,增益值变大。
④高风速时,随着叶片转速的增大,增益值呈先减小后增大的规律。
