一种俯冲改出高度损失量算法分析

刘 晗，马经忠，符围壁，倪金付

(航空工业洪都，江西 南昌，330024)

0 引 言

俯冲指的是飞机在空中以较大角度和速度向下飞冲的机动动作，具有高速度、大俯冲角、大落差的飞行特点，它的轨迹通常可以分为三段，即进入俯冲段、俯冲直线段和改出俯冲段[1]。

图1 描述了飞机完整进入和改出俯冲的飞行过程。首先飞机由中高空A 点进入，在AB 段先操纵副翼使滚转角接近180°，拉杆使俯冲角满足轨迹要求后,再反向操纵副翼使飞机正飞进入俯冲；BC 段为俯冲直线飞行，为满足高精度飞行轨迹的飞行要求，BC段需保持对姿态角的稳定，限定姿态角误差在一定范围之内，要求飞机作无侧滑、无滚转的对称直线飞行，并且要保证直线段俯冲高度H2尽可能大，这就要求AB 段由平飞进入俯冲带来的高度损失H1尽可能小，即需要使飞机尽快进入俯冲段。到达C 点后，飞机进入俯冲改出阶段，有人机俯冲改出过程一般可分两个阶段来完成：首先是驾驶员操纵飞机进入最佳俯冲改出状态，即先消除飞机的不利滚转角等横侧向运动；其次，驾驶员操纵飞机以最佳过载改出俯冲，通过对飞机施加一定的操纵（如在C 点拉杆）使飞机以某一有利的过载改出俯冲，最终推杆使其飞行航迹倾角为零；到达D 点后，飞机进入平飞状态，标志着俯冲完全改出。其中，△H 指的是俯冲改出高度损失量。

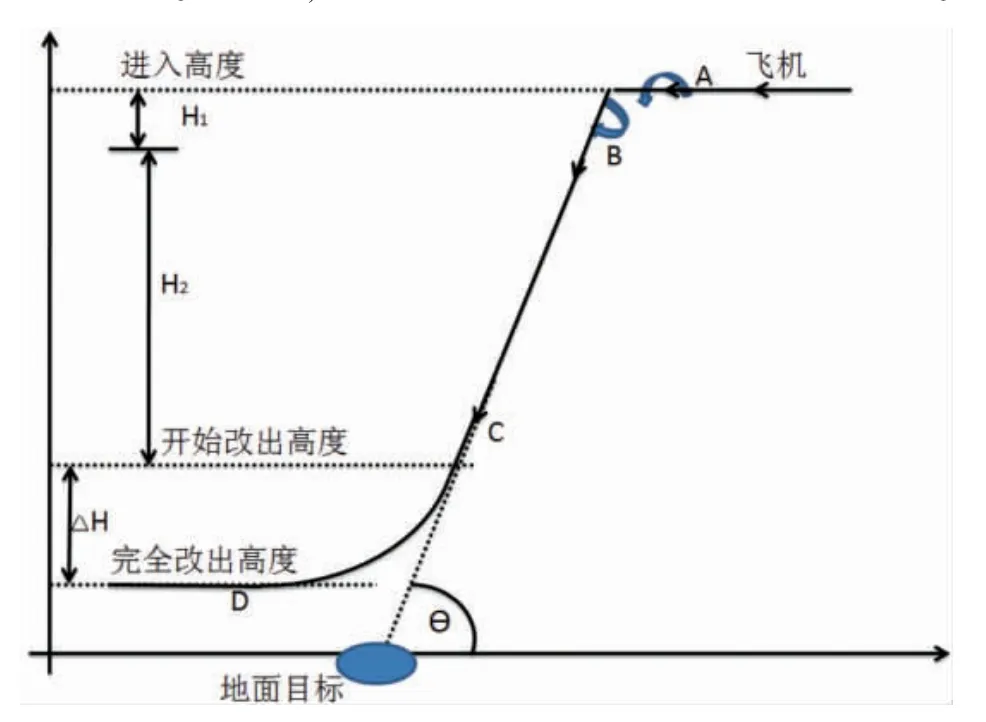
图1 俯冲飞行过程

因在飞行作战和训练中，俯冲是一个极富作战效益和训练价值的常规动作，而俯冲改出段的高度损失量又涉及到飞行安全，是对飞行员心态的极大考验。另外，它还间接影响到作战精确度，因此，工程设计人员和飞行员都对其极为关心。当前的俯冲改出高度损失量大多都依赖于多次的试飞试验，不仅成本高，得出的结果局限性较大，而且还具有一定的试飞风险。试飞过程中对高度损失量的提前预测因理论性不强，预测值与真实值之间的误差量通常也较大。为了让飞行员和工程设计人员能提前准确预测到飞机俯冲改出的高度损失量，保障飞行安全，本文提出了一种在不同飞行状态下飞机俯冲改出高度损失量的理论计算方法，通过将理论结果和实际飞行结果进行对比分析，两者的一致性较好。

1 俯冲的作战训练意义

作为现代战争中空中打击地面目标的主要机动动作，同时在空战中既可作为进攻又可充当防御的战术动作，俯冲有其重要战术意义：

1）在对地作战中，跃升-俯冲攻击战术可有效提高炸弹投掷精度，提高有人机和无人机的作战效果[2]。

2）在执行空地攻击任务接敌时，作战飞机通常都希望有较大的俯冲角，其优点在于：

（1）攻击目标顶部更容易摧毁目标；

（2）可缩短攻击时间，使敌方防空武器来不及准备或准备不充分；

（3）垂直俯冲时空地武器处于目标的正上方，进入敌防空武器（特别是高射炮）的攻击盲区，可以躲避对方攻击，提高自身生存力；

（4）大俯冲角攻击可有效避免地形对成像制导的影响[3]。

3）若相对敌机具备高度上的优势，俯冲机动可保证在使用短射程武器的条件下对敌机进行有效攻击。德军在二战中得出的结论是：在进攻性机动中，采取在高处向下俯冲接敌的攻击方法，成功率最高。

4）作为重要战术选项，俯冲攻击不但自身机动具备高敏捷性的特点，还可赋予攻击战斗机较高灵活性，不仅在俯冲的同时可继续进行纯跟踪，还可避免潜在的地面/空中威胁[4]。

5）在空战射击时的机动占位中，最好的方法是俯冲增速，快速占位后迅速击落敌人，然后拉起飞机[5]。尤其在面对前半球正在上升的敌机时，采取俯冲方式机动占位最为有效。

6）飞机在空战中可以靠跃升和俯冲随意进行高度或速度的互换，在尾追机动中，带坡度的俯冲和上升转弯也具有相当重要的优势。

大多数飞机在无过载/小过载俯冲中加速都非常迅速，这使得俯冲在空战防御机动中也有其重要战术意义。如：防御的一方可采用俯冲加速的方法拉大与敌机的距离； 进行简单俯冲加速并以全功率状态逃离，往往很容易逃脱近距攻击武器的射击范围[5]；在允许的最小速度上突然转向并俯冲加速到最大速度，或高速俯冲至低空，往往可使对手的导弹射击包线缩小；采用俯冲和尾追摆脱的方式可摆脱敌机或退出战斗等等。

另外，由于部分超音速飞机的发动机推力不够大，在执行作战训练任务时，通常可采用在临界音速先俯冲加速，进入超音速后再改为平飞的方法进行超音速飞行。这种方法不仅可以节省燃油，还可大大减小加速的时间。

2 俯冲对飞行人员的要求

俯冲机动意义重大，但对飞行人员却提出了较高要求。日常飞行训练中，当用歼击机进行末端制导阶段作战训练时，飞机通常需尽快进入俯冲（为使俯冲时间最短，飞机通常采用较大负过载由当前状态急滚进入）。如图1 所示，AB 段进入时，必须保证采用的操纵方式不会引发飞机急滚和不稳定，同时保证高度损失量最小；而在BC 段按指定的大俯冲角进行大落差俯冲飞行，并在俯冲直线段需要保持俯冲角、正飞、不能有坡度[6]，满足精确的轨迹跟踪或满足一定的轨迹精度要求。而当用歼击机作俯冲机动飞行时，为避免过载增加过快，飞机却应保持一定的坡度。这样的飞行科目，对飞机的操纵和飞行提出了非常高的要求，特别是如何缩短飞机进入俯冲的时间、减少高度损失和减轻滚转角速度的振荡，快速稳定地达到设定的俯冲角度, 并避免急滚和不稳定[7，8]、迎角和侧滑角发散等问题。

在俯冲改出阶段，驾驶员需要对飞机的多个状态变量（如飞行速度、过载、航迹倾角和滚转角等）进行控制。如在BC 段的末端，飞机的速度可能已经接近速度极限，必须及时以大正过载改出俯冲以保证载机安全。而在作战中，还要求改出俯冲后，飞机的速度V和h 能尽量刚好处于当前能量高度下Ps 的最大值[9]。

俯冲过程中，飞机的俯冲角大，速度快速增加，高度损失量非常大，若飞行员的注意力没有高度集中，飞机就很容易坠地；受地形曲率限制，改出俯冲通常要求使用最大法向过载，但若在高速俯冲情况下生硬拉起飞机，飞机的结构临界载荷将很容易超限，从而导致飞机被肢解；另外，由于俯冲改出迎角持续增加，飞机也容易进入失速。如在海湾战争中，一架伊拉克的MiG-29 在与美国的F-15 对抗时，由于伊军飞行员俯冲改出时的过载超限，而使其丧失态势感知，最终导致飞机出现严重的机头低摇，撞向沙漠。

由于俯冲在作战和训练上的实用性、有效性以及俯冲机动对飞行人员提出的较高要求，为减轻飞行人员的操纵负担，提高飞行安全性，很有必要对俯冲改出高度损失量进行理论计算和分析。

3 俯冲掉高常规算法

俯冲运动可用基本动力学方程组（方程（1））和运动学方程组（方程（2））来描述：

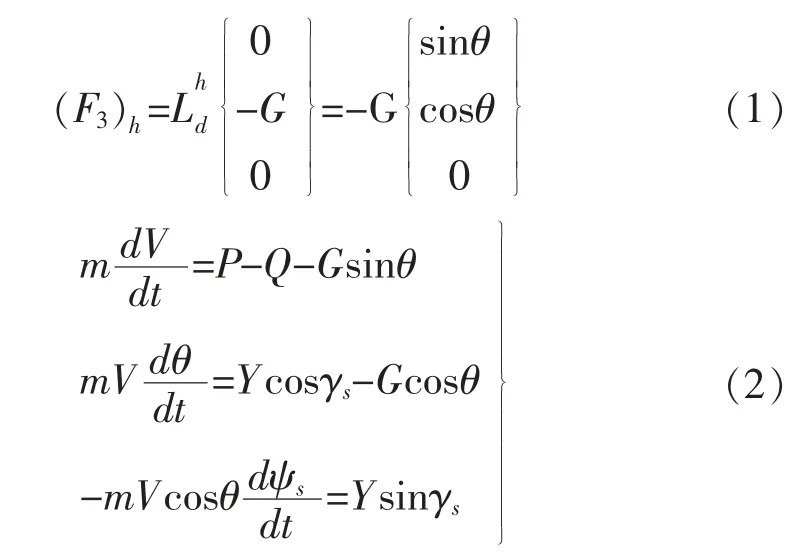
其中，（F3）h 为在航迹坐标系中飞机的重力。

在实际飞行中，俯冲进入段和改出段的速度随时间而改变，很难用一个解析计算公式来求解，用数值积分法计算的工作量又很大，而工程计算方法因对多数方程都进行了大量简化处理，从而导致结果的误差量较大[10]。采用近似解析的计算方法很可能是获取俯冲改出高度损失量的最优途径。飞机俯冲改出段的高度损失量与改出段俯冲角、俯冲速度以及改出过载等参数有关，当机动飞行中无侧滑、无侧力时，方程（1）和方程（2）中的俯冲方程组可简化为：

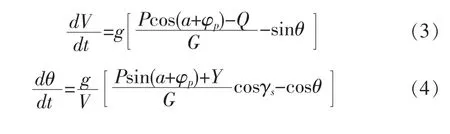
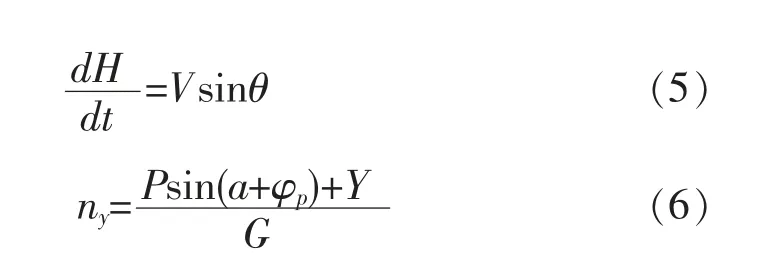
因各型飞机俯冲改出段的发动机状态通常为 “最大” 状态，使用过载为4～5g，按照这样的飞行条件改出俯冲，改出段的速度随时间变化不大。计算时可以用开始改出和改出终了的平均速度进行计算。将方程（6）代入方程（4）可得：

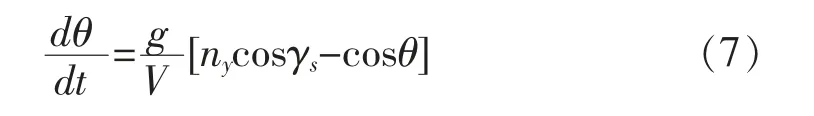
由方程（5）和方程（7）相除可得：

积分后得：

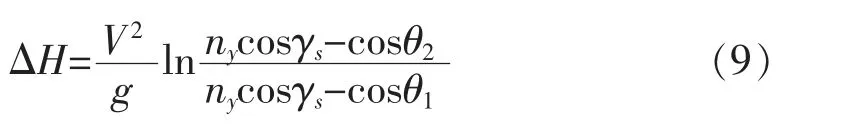
在上述方程中，

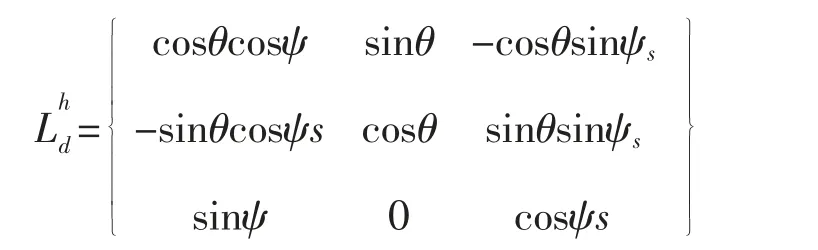
为满足工程计算的需要，计算时认为俯冲改出过程中不存在滚转，且当俯冲角为零时飞机改出，则方程（9）可简化为：

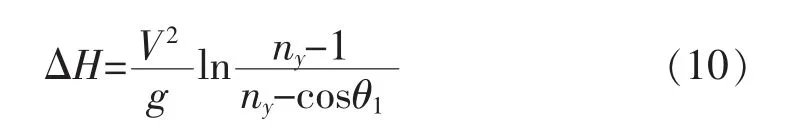
方程（10）中的方法是理论预测俯冲改出掉高时普遍采用的粗略算法。

在保证开始俯冲改出的真空速、俯仰角、改出中最大法向过载等数据完全相同的情况下，将理论计算结果与实际试飞结果进行了对比，如图2 所示。

从图2 可看出，俯冲改出掉高理论计算结果与实际试飞结果相差较大，无法作为试飞参考依据。为便于飞行员预测飞机俯冲改出高度损失量，保障飞行安全，需对原理论计算方法进行修正。

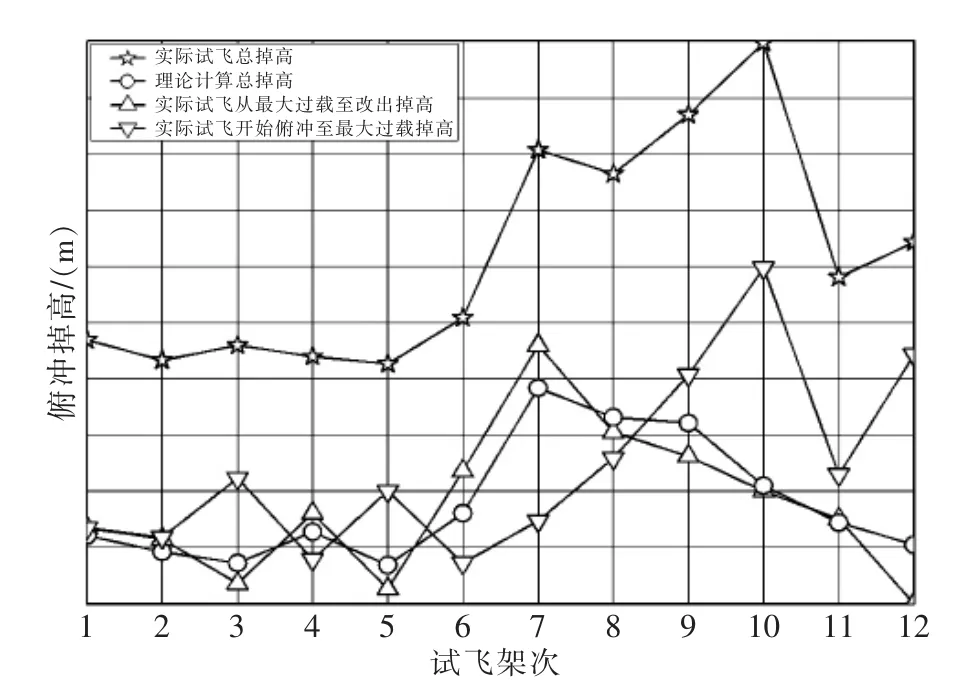
图2 俯冲改出理论结果与试飞结果的对比

4 俯冲掉高算法改进

通过对上述方程的推导过程进行分析发现，在方程（10）的理论计算中，直接采用了改出阶段的过载进行计算。根据实际飞行数据可发现，俯冲改出过程中使用过载一般为4～5g，而飞机到达4～5g 过载需要一定的时间，在这段时间飞机会下降高度，理论计算结果中缺少了这一部分的计算。因此在图2 中，方程（10）的理论计算结果虽与实际试飞结果相差较大，但与从最大过载至改平阶段的掉高差距较小。

开始拉过载改出到拉到最大过载过程中速度变化较小，短时间内俯仰角的变化量也较小，可认为飞机以开始改出俯冲时的俯仰角进行等速等俯冲角下滑（见方程5），该阶段掉高为

方程（11）中，ΔH1为开始拉过载改出到拉到最大过载时的高度损失量；t1为该阶段所经历的时间。

因此可得到从开始拉杆改出到改平后的高度损失量为

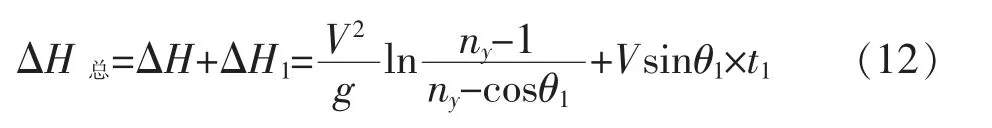
方程（12）为最终获得的飞机在各种不同初始飞行状态下进行俯冲改出时高度损失量的计算方程。其中，t1的值与飞机飞控系统和飞机本体有关，不同飞机对应的t1的值不同，另外飞行员操纵也会影响t1的大小，对于大多数机动型飞机，t1基本都在3s 以内。从作战/训练攻击精确度的角度分析，t1应取机载设备实时测得的从开始改出至最大过载的时间。而从确保飞行安全的角度（如对于心理素质不是很好或初次进行俯冲训练的飞行员在作低空/超低空俯冲机动时），t1值可取保守值，即3s，那么俯冲改出掉高的保守理论方程可写为：

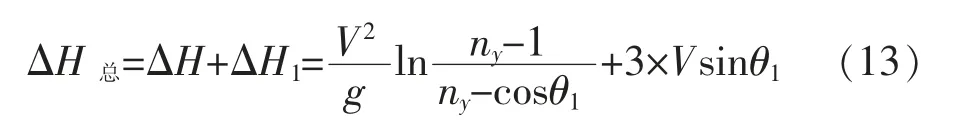
方程（13）为在不同初始飞行状态下飞机进行俯冲改出高度损失量的保守计算方程。在保证开始俯冲改出的真空速、俯仰角、改出中最大法向过载等数据完全相同的情况下，再次将实际试飞结果、修正后的理论计算结果、保守计算结果进行对比，如图3 所示。

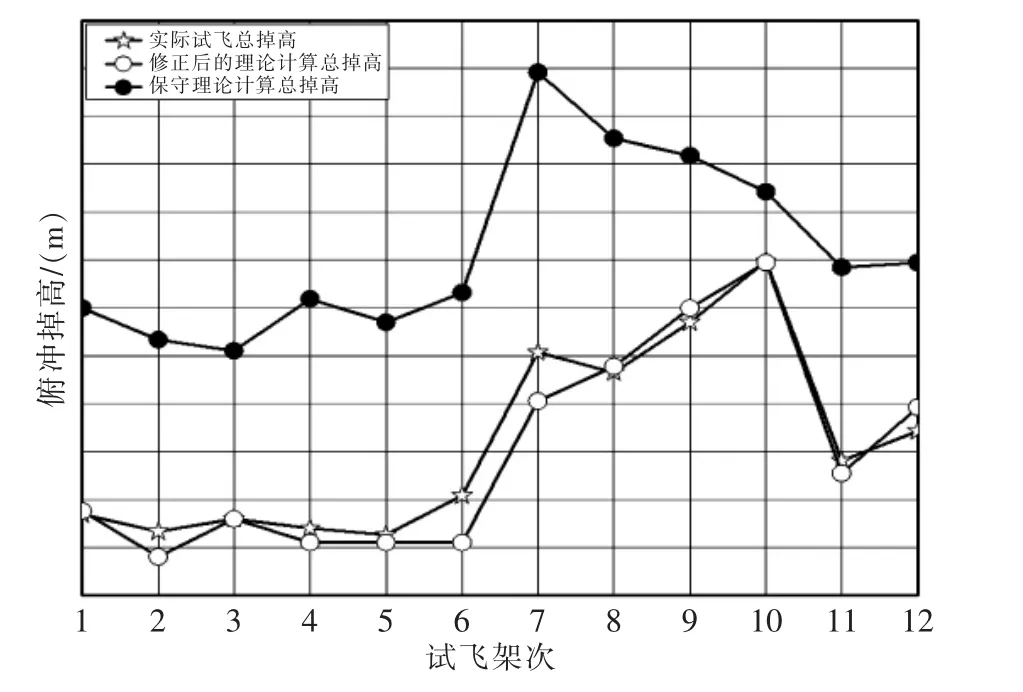
图3 修正后的理论结果与实际试飞结果对比

5 结 语

本文提出了一种俯冲改出高度损失量的理论计算方法，通过将理论结果和实际飞行结果进行对比分析，并对原方法进行了修正。结果表明，实际飞行结果与改进后的理论计算分析结果一致性很好（如图3 所示），此方法合理、有效可行；成本低，没有计算局限性；在保证飞行安全的前提下,保证了俯冲落差和俯冲轨迹精度的实现，提高了试飞效率。另外，由于该方法中涉及到的所有飞行参数，飞行员在执行俯冲机动时通过操纵飞机都可以进行合理的控制，该方法也为飞行员和工程设计人员提前预测飞机俯冲改出高度损失量提供了理论依据和技术支撑，可为飞行员的作战和训练提供参考。