量子粒子群算法反演概率积分法参数

朱尚军 王 磊， 魏 涛 蒋 创 江克贵 查剑锋 孔 川4

（1.安徽理工大学空间信息与测绘工程学院，安徽淮南232001；2.中国矿业大学环境与测绘学院，江苏徐州221116；3.江苏省资源环境信息工程重点实验室，江苏徐州221116；4.山东裕隆矿业集团有限公司单家村煤矿，山东曲阜273100）

概率积分法参数预计是我国《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采指南》中常用的开采沉陷预计方法，其中概率积分法参数反演是地表移动观测数据处理的关键环节之一［1-2］。概率积分法是我国研究开采沉陷较为成熟且应用较为广泛的预计方法之一［3］。该方法是以正态函数为影响函数，采用概率积分方法表示地表移动盆地的下沉、倾斜、曲率、移动和变形［4］。精确反演概率积分法参数是提高开采沉陷预计精度的基础，但由于概率积分模型是多参数非线性模型，从而导致参数反演过程异常复杂和困难［5］。

反演概率积分法参数常用的方法有直接求参、拟合求参和智能优化算法求参，其中智能优化算法可以弥补反演概率积分法参数过程中计算量大与过程复杂等不足。近年来，不少学者将智能优化算法应用于概率积分法参数反演研究，取得了一定的进展。吴侃等［6］将模矢法引入概率积分法参数反演中，在此基础上开发了矿区沉陷预测预报系统，并结合无人机、三维激光扫描仪等新技术建立了一系列变形监测模型；查剑锋等［7］通过研究论证了遗传算法在概率积分法参数反演中的适用性与稳定性，但该算法易陷入局部最优解；徐梦强等［5］将算法简单、精度高的粒子群优化算法引入概率积分法参数反演中，利用模拟试验和工程应用实例证明了该算法的有效性，但该算法存在易陷入早熟收敛、粒子全局搜索效果较差、收敛速度较慢等不足；陈涛等［8］提出了基于果蝇算法的概率积分法参数反演方法，通过矿山实测数据验证分析，证明了该算法有助于提高概率积分法参数反演精度。通过分析研究成果可以发现：①当算法搜索领域不够充分时，上述遗传算法、粒子群优化算法、果蝇算法等都会在一定程度上陷入局部最优，从而导致算法早熟收敛［2］；②粒子群优化算法在参数反演过程中存在参数选择困难、早熟收敛、全局搜索效果较差、算法运行耗时较多等不足［9-13］。通过查阅相关成果［9-10］发现，通过加入量子化引力场，有助于提高智能优化算法的运行效率。魏涛等［9］将量子算法即量子旋转门引入遗传算法中，提高了算法的准确性与稳定性，并克服了传统遗传算法易陷入局部最优的缺陷。借鉴上述研究思路，如果将量子化引力场引入粒子群优化算法中，利用该算法的运行效率优势，将搜索域扩大为全局搜索且降低陷入早熟收敛的概率，那么优化后的算法（即QPSO算法）在概率积分法参数反演中相对于传统粒子群优化算法而言，势必会具有一定的优势。为此，本研究提出了一种基于QPSO算法的概率积分法参数反演方法，并对其适用性进行讨论。

1 基于QPSO的概率积分法参数反演模型

1.1 理论基础

粒子群优化（PSO）算法作为一种基于群体智能的优化算法，是由1995年美国心理学家James Kennedy和电气工程师Russell Eberhart提出［14］。PSO算法属于群体智能优化算法范畴，源于模拟鸟群的觅食过程，通过个体之间相互合作最终找到食物最多最近的点，即优化后的搜索结果［5］。孙俊等［11］提出了量子粒子群（QPSO）算法，该算法取消了速度变量，并且位置更新是完全随机迭代，弥补了PSO算法的不足，是一个有效且较为完善的群体智能优化算法。

有别于传统PSO算法，QPSO算法并非让粒子按照某一随机确定的轨道移动，而是建立一个量子化引力势场来束缚粒子运动。在建立量子粒子群模型时，用向量X表示粒子个体的当前位置，即粒子个体的思维状态；随后经过适应度函数判定找到个体的历史最优位置，即粒子个体的最优历史经验；gbest表示由N个粒子组成的粒子群中适应度函数最优的粒子当前位置。在物理力学中用束缚态来描述聚集性，粒子运动中心存在某种引力势场是粒子产生束缚态的主要原因［11］。因此建立一个量子化引力势场是量子粒子群优化算法的基础，处于引力势场的粒子会依据一定的概率出现在解空间的任何一个位置，当趋近无穷远时，粒子出现的概率趋于0。可见，QPSO算法的随机性远大于PSO算法，如何建立一个引力势场至关重要［15］。

1.1.1 势场模型建立

式中，i、j分别为粒子个数及维数；t为迭代次数；N为粒子总数；c1、c2为加速常数；r1、r2为区间(0,1)上的随机数；Gij(t)为历史全局最优位置。

由式（1）和式（2）可知，当c1=c2时，φij(t)即为在区间(0,1)上随机且均匀分布的一个数。因此可将式（2）中φij(t)表示为直接由随机数产生，可将式（2）表示为

在量子粒子群算法中采用该式表示历史最优位置与群体最优位置之间的某个随机多维点的位置。

由上述分析并依据文献［14］提出在pij点建立δ势阱引力场。由于粒子的位置和速度在量子化空间中无法同时确定，所以需要利用波函数ψ(x,t)（x为粒子的位置，t为粒子的速度）来描述粒子的运动状态，粒子的空间三维坐标向量为X=(x,y,z)。波函数表述的物理意义为粒子在解空间某点出现的概率等于波函数模的平方，可表示为

式中，Q(X,t)为概率密度分布函数。

易知，式（4）满足归一化条件

式（5）即为Schrodinger公式，是粒子在量子空间中的动力学方程［11］。

为求得多维δ势阱下粒子的随机位置方程，先在一维空间中建立一个一维势阱，表达式为

式中，x,y为一维条件下点的坐标；p为δ势阱引力场一维坐标；γ为常数。

令y=x-p，Schrodinger公式可改写为

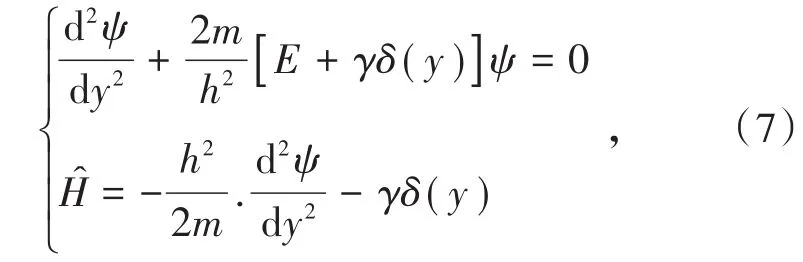
Schrodinger公式在一维条件下的解为

式中，L为势阱的特征长度；β为势阱的特征长度的倒数。

通过式（6）、（7）、（8）求得粒子出现在解空间的概率分布函数。为求得粒子在每点的适应度值，需求出粒子在解空间的确切位置x，进而得到粒子的位置更新公式。

1.1.2 QPSO算法粒子位置进化方程

在上文已求得一维条件下的波函数，即得到了粒子相对于pij点的位置。为求得粒子的确切位置，本研究采用蒙特卡罗随机模型（逆变换法）方法［11］推导出一维δ势阱下粒子的随机位置方程：

式中，u为区间(0,1)上的随机数；p为δ势阱引力场一维坐标。

将一维拓展为多维，即在每一维上都建立一个一维δ势阱，可得粒子i的随机位置方程（即位置进化方程）：

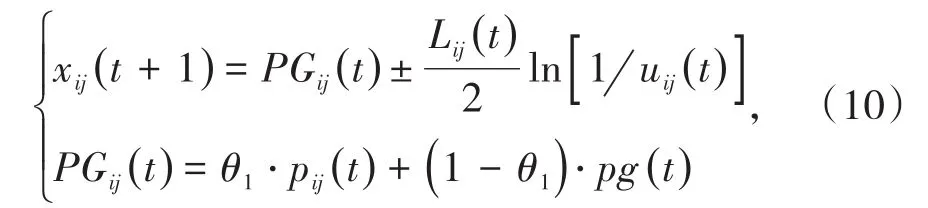
式中，θ1为区间 (0,1)上的随机数；t为迭代次数；xij(t+1)为第t+1次迭代中粒子i的位置；PGij(t)为第t次迭代中粒子的历史最优位置pij与群体最优位置pg之间的某个随机多维点的位置；Lij(t)为多维条件下的势阱的特征长度。

对函数Lij(t)进行控制时的运算公式为

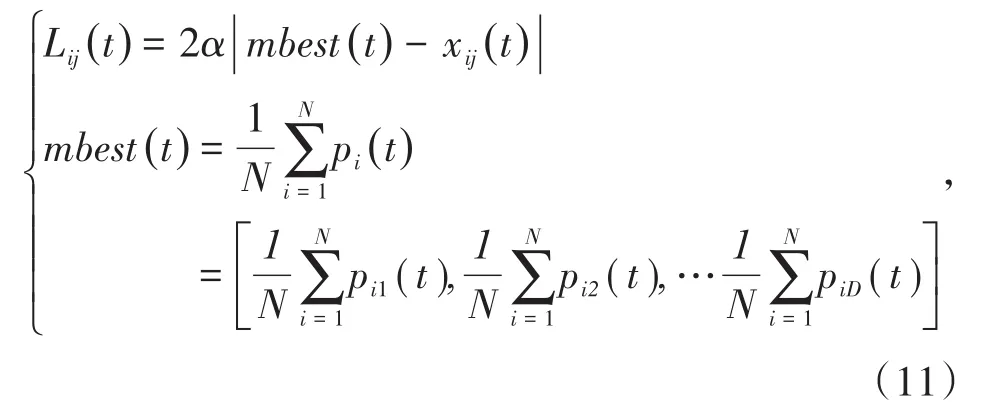
式中，D为粒子维数；mbest(t)为所有粒子个体的历史最优位置的均值；N为粒子总数；α为收缩因子是量子粒子群中唯一需要确定的参数，是用来控制量子粒子群的收敛速度，即扩张收缩速度［16-17］。

式（11）中参数α控制公式为

式中，T为算法的总迭代次数［4］；t为算法的当前迭代次数；αmin与αmax为常数，通常αmax取1、αmin取0.5。本研究αmax取1，αmin取0.5。

综上分析，可得粒子的进化公式为

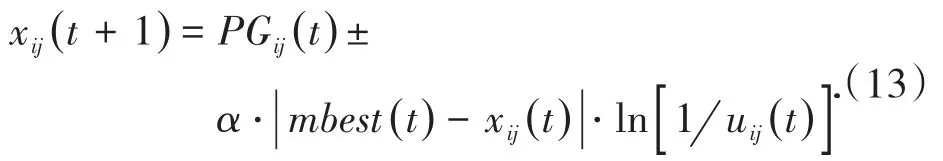
通过上述分析可知：QPSO引入平均个体历史最优位置，取消了速度向量，将粒子搜索区域扩大为全局唯一的解空间；在平均位置的作用下每个粒子在收敛过程中不得不考虑其他粒子的运动状态而独立地向最优点gbest靠近，远离gbest的粒子会将平均位置拉向自己，此时聚集于gbest附近的粒子大范围搜索最终的群体最优位置，等远离的点靠近gbest时再共同缩小搜索区域，故而加强了粒子的全局搜索能力，降低了粒子陷入局部最优的概率［15-21］。

1.2 基于QPSO算法的概率积分法参数反演模型构建

根据概率积分法原理［1-5］，可将地表任意一点的下沉值与水平移动表示为

式中，P为概率积分法参数矩阵，P=[q,b,tanβ,θ,S1,S2,S3,S4]；q为下沉系数；b为水平移动系数；tanβ为主要影响角正切值；θ为开采影响传播角；S1，S2为上下拐点偏移距；S3，S4为左右拐点偏移距；（x，y）为观测站点的坐标

假设地表任意一点M的实测下沉值与水平移动值分别为WM实，UM实，该点通过QPSO算法得出的下沉与水平移动预计值分别为WM实，UM实.则该点的下沉与水平移动残差vM为

式中，abs为绝对值运算方式；sum为求和运算方式。

根据误差平方和最小原则，本研究构建的概率积分法求参准则为

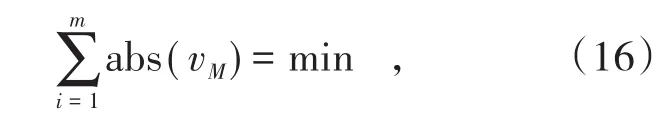
式中，m为测点数，i＜m。可根据该式采用QPSO算法求解概率积分法参数。

综上分析，本研究采用MATLAB语言对QPSO算法进行编程实现。假设在解空间有100个粒子，每个粒子有8维，在第t次迭代中粒子的当前位置可表示为xi8=[xi1(t),xi2(t),…,xi8(t)],i=1,2,…,100；粒子的历史最优位置可表示为pi8(t)=[pi1(t),pi2(t),…,pi8(t)]，群体最优位置可表示为pg8(t)=[pg1(t),pg2(t),…,pg8(t)]。将下沉和移动变形实测值与预计值之差的绝对值累加值作为适应度函数f：

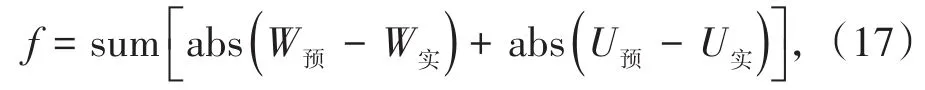
适应度函数越小说明粒子位置越好，即参数反演结果越好。

本研究基于QPSO算法的概率积分法参数反演流程如图1所示。

算法实现步骤为：

（1）初始化种群，将粒子当前位置初始化为个体历史最优位置，计算适应度找到群体最优位置。

（2）通过式（10）得到粒子i(1≤i≤100)的介于个体历史最优与群体最优之间的位置PGi。

（3）依据式（11）计算mbest，即个体历史最优位置的均值。

（4）根据式（13）更新粒子的位置。

（5）计算当前迭代次数下的粒子适应度值，并与前一次迭代比较，如果适应度值小，将粒子历史最优位置更换为当前粒子的位置；否则，不变。找到群体最优位置与前一次迭代结果比较，适应度值小，则进行替换；否则，不变。

（6）重复步骤（1）至步骤（5），若循环达到最大迭代次数或满足精度，则跳出循环，输出最终反演所得的8个概率积分法参数。

2 模拟试验

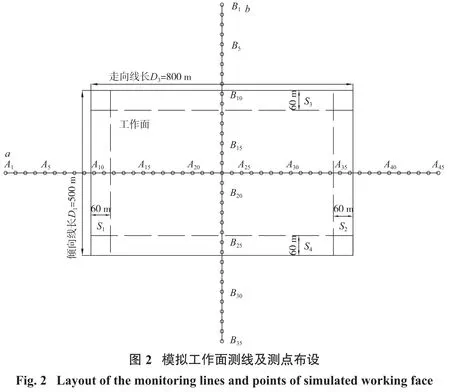
2.1 工作面概况

本研究所模拟的工作面煤层采厚为3.0 m，煤层倾角为5°，走向线长800 m，倾向线长500 m，平均采深为400 m，采用全部垮落法顶板管理，达到充分开采。地表沉陷预计的概率积分法参数设计为：下沉系数q为0.8；主要影响正切tanβ为2.5；水平移动系数b为0.25，开采影响传播角θ为85°；拐点偏距（S1=S2=S3=S4）为0.15倍的平均采深，即60 m。在试验中，在移动盆地内设计了沿走向和倾向2条主断面的移动和变形观测线，每个监测点间距为30 m，其中走向线（a线）长度为800 m，共布设了45个监测点；倾向线（b线）长度为500 m，共布设了35个监测点。模拟工作上的测线及测点分布如图2所示。

2.2 QPSO及PSO算法参数反演准确性及效率比较

本研究使用QPSO及PSO两种智能优化算法对概率积分法参数进行反演，将下沉与水平移动残差绝对值之和作为适应度函数；再将参数设计值与参数反演值进行比较，通过比较求取参数的相对误差和中误差的大小反映参数反演的准确性，并进一步分析比较两种算法的运行时间。为了避免求参偶然误差，在相同条件下分别进行了10次试验，结果如表1所示。

注：PSO与QPSO算法参数取值是通过10次试验取均值得到；10次试验中，PSO与QPSO算法运行耗时分别为1 665.43 s和197.79 s。

由表1可知：①QPSO算法反演的概率积分法参数中除了θ值中误差略大外，其余参数的中误差均小于PSO算法反演的参数中误差，表明QPSO算法的稳定性优于PSO算法；②QPSO算法反演的概率积分法参数除了部分拐点偏距（S1、S2）的参数相对误差略大外，其余参数的相对误差都小于PSO算法，反映出QPSO算法反演精度优于PSO算法；此外，QPSO算法耗时也远小于PSO算法，表明QPSO算法的运行效率优于PSO算法。

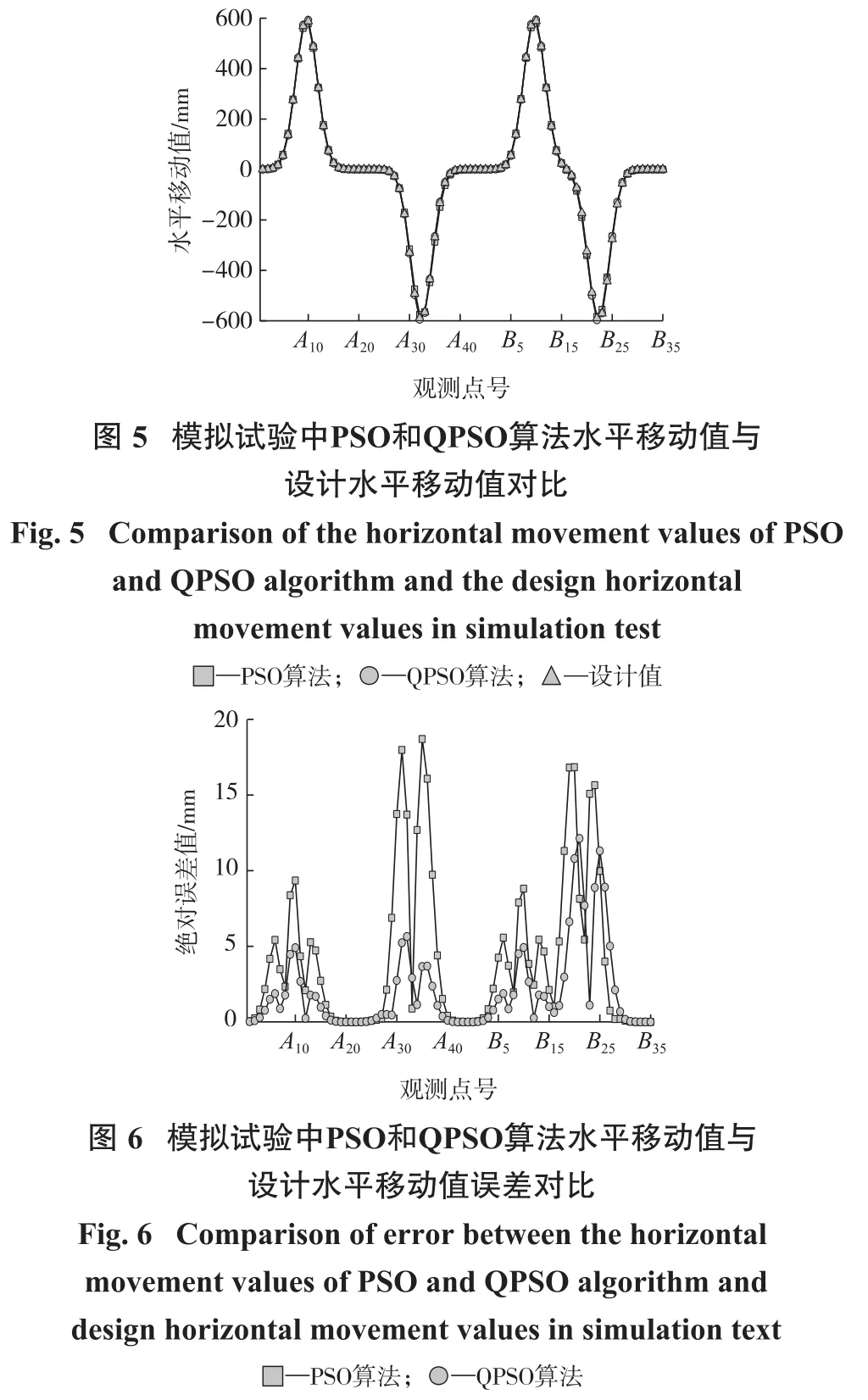
为了进一步分析两种算法的参数反演效果，根据QPSO与PSO算法的概率积分法参数反演结果，绘制了两者的下沉曲线及水平移动曲线，如图3至图6所示。

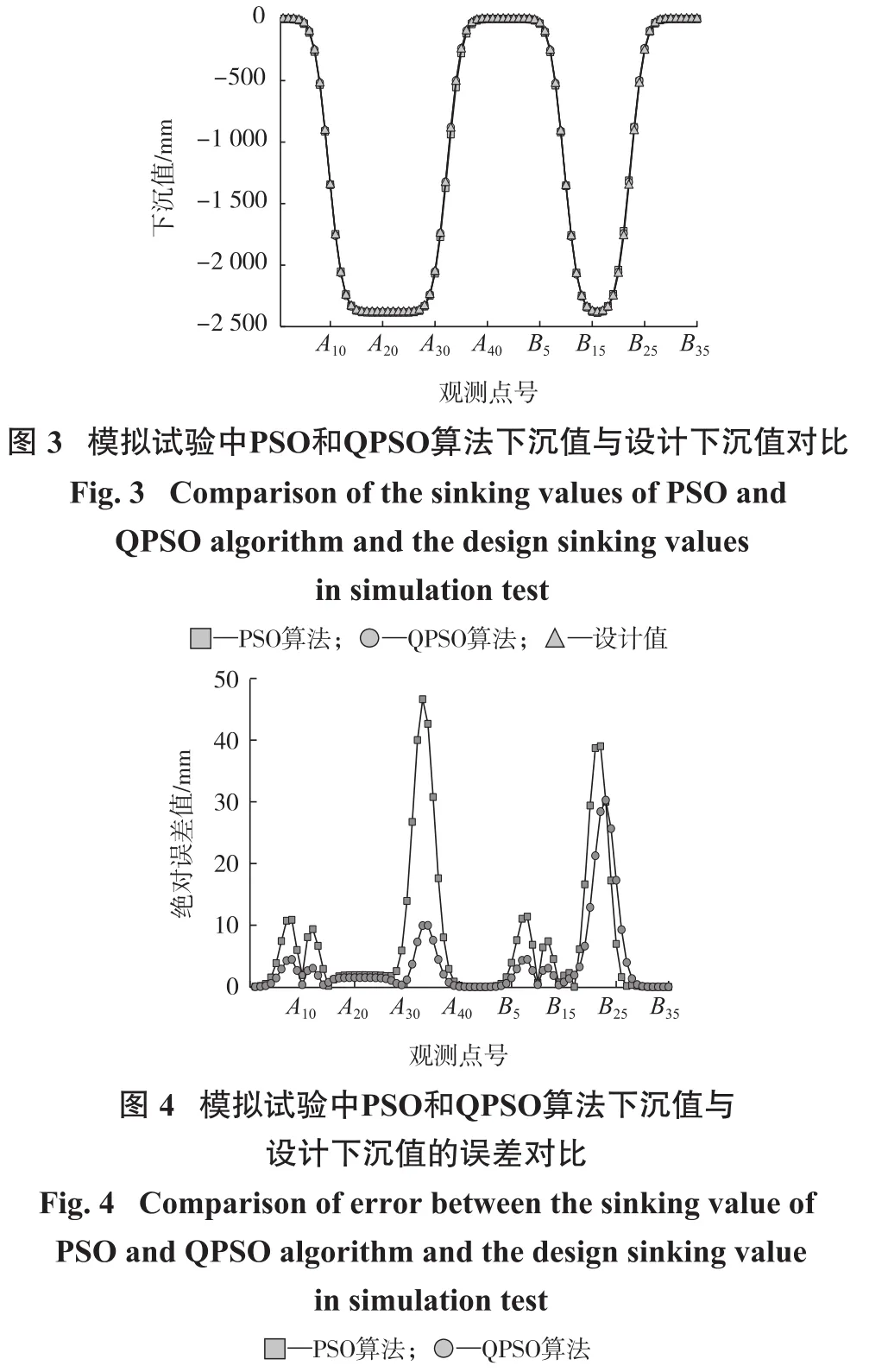
由图3至图6分析可知：PSO及QPSO算法的下沉及水平移动拟合效果均较好；QPSO算法的绝对误差波动小于PSO算法。通过模拟试验数据计算得PSO的参数取均值后求得的下沉值与水平移动值的拟合中误差为8.50 mm；QPSO的参数取均值后求得的下沉值与水平移动值拟合结果中误差为3.19 mm。可见，QPSO算法概率积分法参数反演精度优于PSO算法，并且QPSO算法的运行效率远高于PSO算法。

2.3 QPSO算法可靠性研究

对表1进一步分析可知：①利用QPSO算法进行10次概率积分法参数反演后，参数的最大相对误差不超过±4%，说明采用QPSO算法反演概率积分法参数精度较高；②与PSO算法相比，QPSO算法反演的概率积分法参数除了影响传播角θ拟合中误差略大外，其余参数的拟合中误差均小于PSO算法，说明QPSO算法稳定性优于PSO算法；③QPSO算法运行效率也明显优于PSO算法。模拟试验结果反映出QPSO算法可靠性较好。

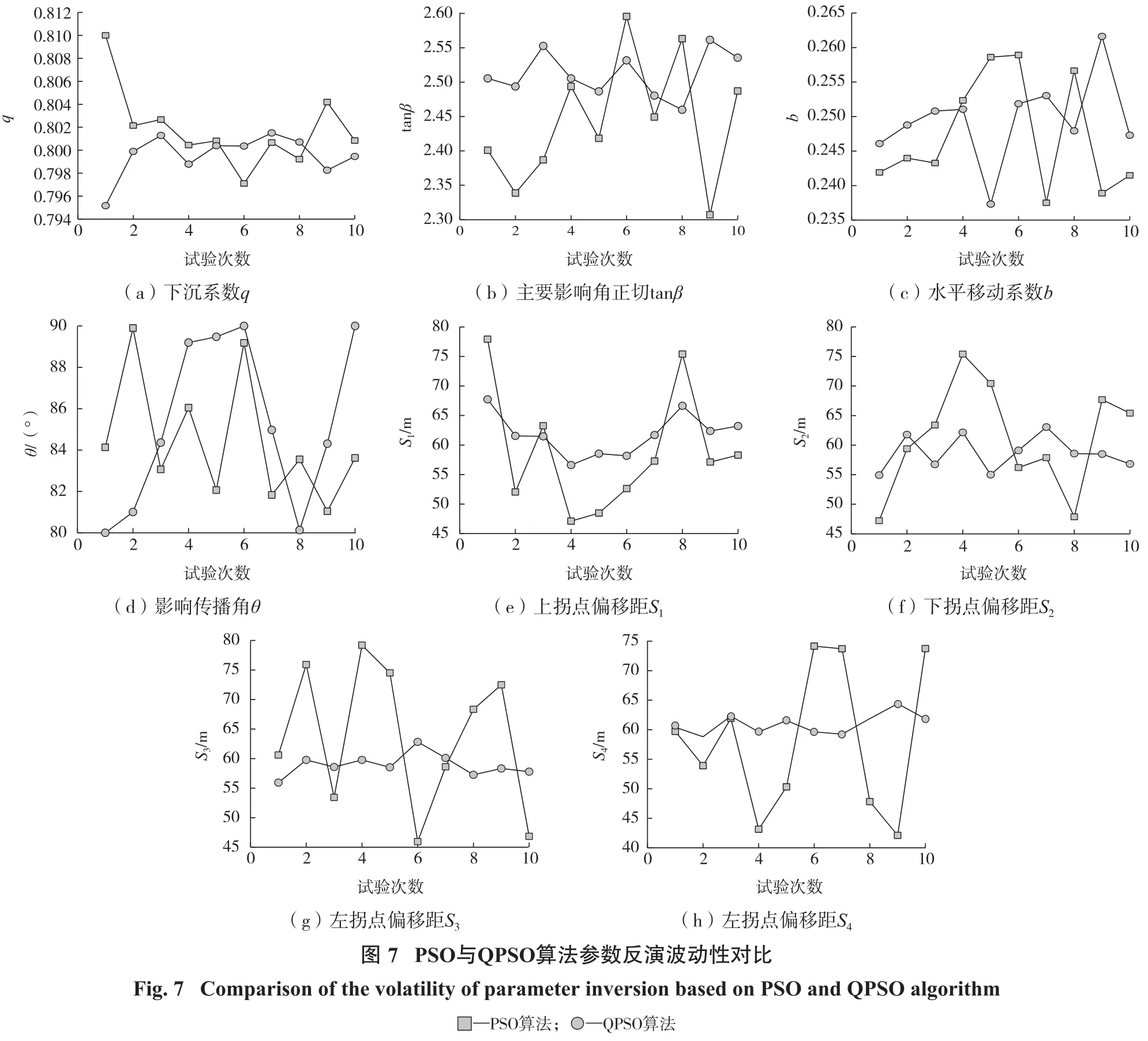
为了进一步分析QPSO算法的稳定性，本研究对PSO与QPSO算法反演的参数分别进行了波动性分析，结果如图7所示。

由图7可知：QPSO算法参数反演结果中除了影响传播角θ波动略大外，其余参数的波动性均小于PSO算法反演的各个参数。

3 工程实例

3.1 矿区概况

淮南顾桥矿南二采区1414（1）是该矿南区的首采工作面，该工作面采用后退式开采，机械化掘进，一次采全高，全部垮落法管理顶板。该工作面沿煤层走向布置，工作面开采尺寸为走向长度×倾向长度为2 120 m×251 m，工作面走向方向为充分采动，倾向方向为非充分采动，总体为非充分采动［22］。工作面平均采高为3.0 m，煤层倾角平均为5°，为近水平煤层。工作面平均深度为735 m，倾向观测线布置在距离切眼和停采线1 144 m和976 m处，共布设了3个控制点和50个监测点，点间距为30 m，倾向线长度为1 500 m。

3.2 试验结果及分析

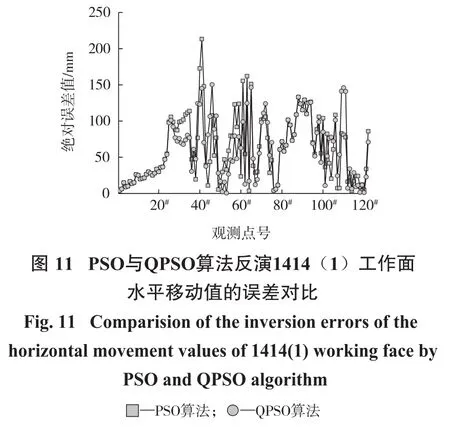
选取顾桥南矿1414（1）工作面122个监测点（走向线上75个监测点，倾向线上47个监测点）的实测数据为基础，分别采用基于QPSO、PSO算法构建参数反演模型对该工作面进行概率积分法参数反演，并对结果进行对比分析。两种模型分别进行了10次试验，将试验结果取平均值，并计算参数的拟合中误差，结果如表2所示，拟合结果分别如图8至图11所示。

由表2以及图8至图11分析可知：QPSO算法反演参数得到的拟合中误差均优于PSO算法，可认为QPSO算法稳定性较好，并且QPSO算法效率明显优于PSO算法；PSO与QPSO算法的拟合结果都较为精确，将两种智能优化算法反演的参数取平均值，计算出PSO算法下沉值、水平移动值与实测下沉值、水平移动值拟合中误差为70.93 mm，QPSO算法下沉值、水平移动值与实测下沉值、水平移动值拟合中误差为72.04 mm，两种算法的下沉值与水平移动值拟合精度相当。根据文献［9］分析可知，尽管二者的拟合精度都符合工程应用标准，但QPSO算法运算效率相对于PSO算法有明显优势，故QPSO算法对于实现概率积分法参数高效率、高精度反演有较好的适用性。

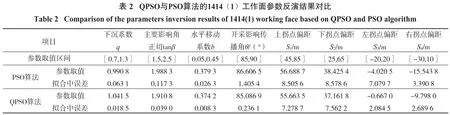
注：概率积分法参数取值区间是根据1414（1）工作面已有资料得出；10次试验中，PSO与QPSO算法运行耗时分别为1639.43 s和197.72 s。

4 结语

为实现对概率积分法预计参数的精确反演，提出了基于QPSO算法的参数反演模型。模拟试验以及顾桥南矿1414（1）工作面实例分析表明：QPSO算法模型反演参数的波动性略小于PSO算法模型，并且QPSO算法模型的运算效率明显优于PSO算法模型，对于实现概率积分法开采沉陷预计参数高效、精准反演有一定的参考价值。