岩体质量分级的改进模糊综合评价法

2020-08-15尹会永赵翠月马登贤丛顺明

金属矿山 2020年7期

尹会永赵涵徐琳赵翠月马登贤丛顺明

（1.山东科技大学地球科学与工程学院，山东青岛266590；2.山东省第八地质矿产勘查院，山东日照276826；3.山东黄金矿业（沂南）有限公司，山东临沂276317）

在地下工程建设中，岩体质量分级是地下巷道工程设计的基础，对岩体进行合理的质量分级，有助于认识岩体力学特性及选取合理的技术参数，对于保障地下工程安全施工、正常运行具有重要意义［1］。传统的岩体质量分级方法主要有BQ工程岩体分类法、RMR分级法、Q系统分级法等，这些方法选择不同的评价指标对岩体质量进行分级，形成了较为严谨的体系，推动了岩体质量分级理论的发展，在工程上应用较为普遍［2］。但这些传统分类方法也存在一定的不足：BQ法对于抗压强度这一指标过于敏感，并且弱化了修正因素所造成的影响，经过大量实践证明，其评价结果偏保守；RMR法采用分段评分，不具有连续性，容易造成最终得分的急剧变化［3］；Q分级法缺乏对岩体强度方面的考虑［4］，并且将岩体分为9类，过于繁琐。

近年来，随着岩石力学理论的发展，越来越多的岩体质量评价体系不断被建立，属性识别理论［5］、神经网络法［6］、灰色聚类法［7］、模糊综合评价法［8］、可拓学理论法［9］等理论被运用于围岩质量分级中，并取得了一定的成果。该类新型方法的共性在于：①所考虑的核心因素由岩体强度过渡到岩体结构特征；②由仅考虑岩体自身特征过渡到岩体所处的环境条件；③由定性分级过渡到定性与定量综合分级［10］。基于模糊数学理论的模糊综合评价法具有建模简单，易于掌握，对多因素、多层次的复杂问题评价效果好的特点［11］，对于岩体质量分级这类评价标准相对模糊的问题，具有很好的适应性，优势较明显。但是，传统的模糊综合评价法中权重赋值比较片面，并且多采用最大隶属度原则做决策，可能造成数据信息丢失与说服力不足的问题。因此，为了尽可能减少主观因素在确定评价指标权重时产生的影响，本研究通过熵权法确定权重系数，并在评价结果中引入有效度来对最大隶属度原则进行修正，建立了改进的模糊综合评价模型，使岩体质量分级评价结果更加精确合理。

1 模糊综合评价法基本原理

模糊数学理论的核心主要分为3个部分，即隶属度计算、权重赋值以及综合判定原则。

（1）确定模糊指标集和评价集。定义岩体质量评价的指标集U={u1,u2,…,un}，ui(i=1,2,…,n)是岩体质量评价因子；定义V为岩体质量评价的评价集，V={v1,v2,…,vm}，vj(j=1,2,…,m)是岩体质量评价的等级。

（2）建立单因子评价矩阵R。设rij表示第i种评价指标可以被评价为第j等级的可能性（即i对j的隶属度，它们的关系即为隶属函数［12］），可以得到总体评价矩阵：

（3）对各指标的权重进行赋值，计算出综合评价结果向量。由于指标集U中各评价指标在岩体质量综合评价中的作用、影响、贡献等重要程度不一，因此，需要对参与评价的各指标定义一个权重集：

通过复合运算将权重向量与总体评价矩阵相结合，得到模糊综合评价结果：

式中，∘为模糊合成算子；根据最大隶属度原则有b=max{bj}(j=1,2,…,m)，为岩体质量综合评价等级。

2 模糊综合评价法岩体质量分级过程

2.1 岩体质量影响参数选取

根据《工程岩体分级标准》（GBT 50218—2014）以及对各种岩体质量评价方法的对比与分析，综合选取5个指标作为分级评价依据，既考虑了岩体自身物理力学特性，又考虑了可能影响岩石强度的指标，既有经验判断，也有测试计算。所选取的指标为单轴饱和抗压强度Rc、完整性系数Kv、岩石基本质量指标RQD、结构面影响系数和地下水影响系数。其中，结构面影响系数和地下水修正系数为定性指标，通过实地考察与专家评分来使之定量化。结合选取的5个评价指标，将巷道围岩等级分为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ共5个等级，具体分级标准见表1。

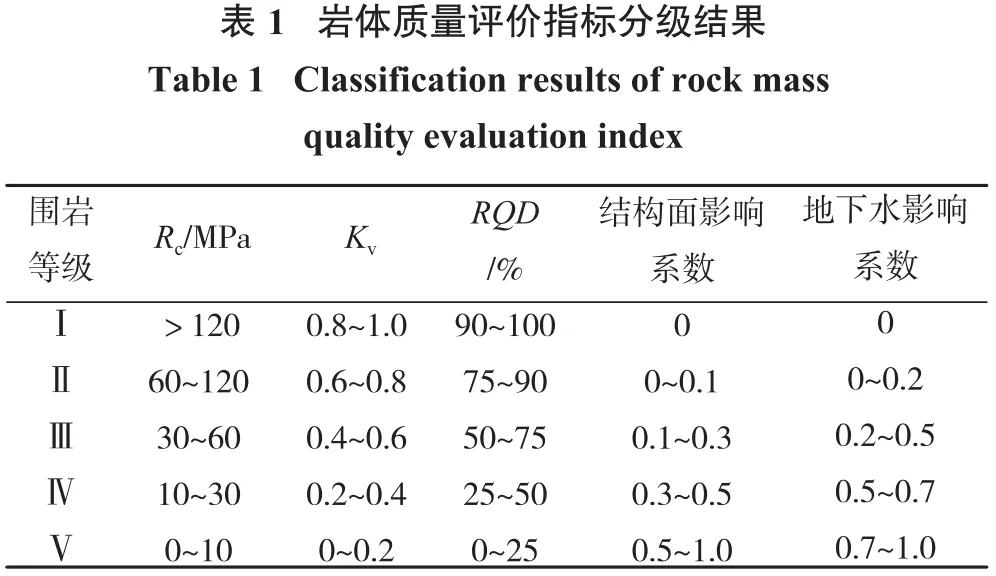
注：地下水修正系数分为潮湿、点滴出水、淋雨状出水、线流状出水、涌流状出水5个定性状态进行定量化表示；结构面影响系数通过对实测的节理间距和结构面长度进行专家打分，最好为0分，最差为1分。

2.2 确定隶属函数

对于定量化描述的岩体材料参数来说，每个等级区间存在一个指标，当因子取值靠近指标时，属于此等级的概率越来越大，最高为1，因此可以用正态分布函数来表示隶属函数［13］

式中，k、t为常数，k＞0、t＞0。

正态隶属函数模型如图1所示，图中V表示x取值隶属于当前等级的最大概率，通常为1。

式（4）中k、t值的计算过程如下：

（1）当x取某等级区间的中间值时，此时属于此等级概率为1，即，此时x=k，可得

式中，x上、x下为相应指标的上下界限。

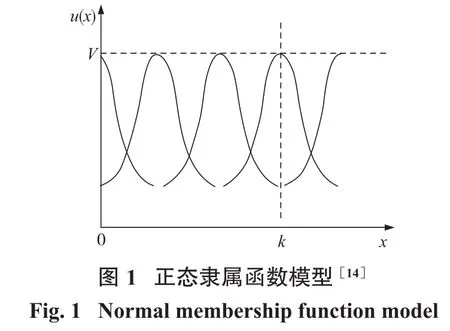
（2）当x取值介于两等级之间时，此时属于两种等级的概率相同，将式（5）代入（4），即，可求得

经过计算得出本研究所选定的5个指标的k、t值如表2所示。

2.3 确定各指标的权重

岩体质量分级是一种多指标的评价体系，对于多指标评价来说，客观确定各指标的权重对于评价结果有关键影响，确定权重的方法主要有层次分析法［15］、数理统计法、德尔菲法［16］、熵权法等。其中熵权法是一种将各指标信息进行量化综合然后赋予权重的方法，计算结果客观合理，已被广泛应用。故本研究采用该方法确定权重，步骤如下：

（1）假设有m个评价点(i=1,2,…,m)和n个评价指标(j=1,2,…,n)，可以构成一个初始判断矩阵Y：

（2）由于各评价表单位不同，量级尺度也不同，直接进行计算会对权重结果造成影响，为了消除这一影响，利用归一化原则将矩阵Y转化为归一化后的矩阵E，对于正向指标有：

对于逆向指标，则有：

（3）根据熵概念计算各指标的信息熵。公式为

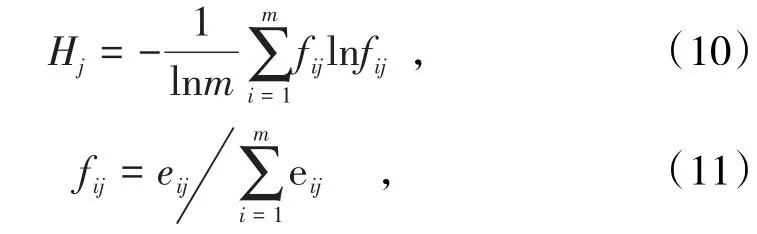
式中，Hj为j项指标的信息熵。为了避免fij等于0导致lnfij无意义，故而对fij进行了如下修正：

（4）计算各评价指标的熵权。信息熵越小，说明该指标在岩体质量评价中所起的作用越大［17］。第j项指标的权重ωj为

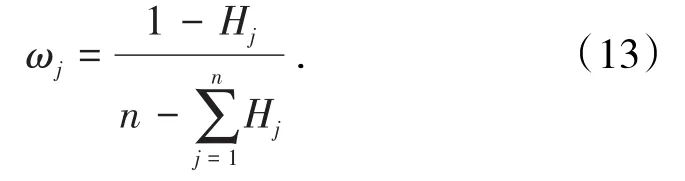
2.4 模糊综合评价

模糊算子的选择对于评价结果有重要影响，常用的运算模型有取小取大型、相乘取大型、相乘相加型、取小相加型［18］。由于取小取大型和相乘取大型强调主要质量指标的影响，容易造成数据丢失，取小相加型会忽视某项指标较大情况下的影响。因此本研究采用相乘相加型计算模型，兼顾所有指标对质量分级的影响，能够比较真实地反映出岩体质量的综合状况，所得出的模糊评价结果为

式中，W为权重矩阵；R为评价矩阵。

传统的模糊综合评价法一般根据最大隶属度原则来判断岩体质量等级，但是当综合评价矩阵B中有两个隶属度非常接近的情况下，使用最大隶属度原则就会影响评价结果的可靠性，使评价结果无法反映真实情况。因此定义最大隶属度原则的有效度α为［19］

式中，n为综合评价矩阵B中元素个数；β为最大隶属度；γ为第二大隶属度。

本研究设定当α≥0.5时，应用最大隶属度原则比较合理；α＜0.5时，最大隶属度原则的评价结果不可靠，此时采用加权平均原则求出对象的隶属等级［20］：

式中，bj为评价对象对于第j等级的隶属度；c为加权系数，一般取1或2，本研究取2，目的是控制较大的bj起作用。

本研究改进的模糊综合评价实现流程见图2。

3 应用实例

以山东黄金沂南金矿金场矿区为研究对象，矿区拟开拓巷道及采场位于马旺矿段及冶官墓矿段深部的断层破裂带中，岩体蚀变严重，节理裂隙极为发育［21］，围岩稳定性影响因素错综复杂。如何合理评价岩体质量等级，成为巷道掘进与支护最基本也是最关键的工程地质问题之一。本研究选取该矿右2巷道0～10 m、10～20 m、20～30 m、30～44 m、矿体上、矿体下共6段进行岩体质量分级。上述6段巷道围岩参数取值如表3所示。

通过式（7）至式（13）可求得权重集W：

W=(0.22,0.23,0.21,0.14,0.20)，

以第一段0～10 m巷道为例，根据式（4）及表3建立了单因子综合评价矩阵R：

则综合评价结果B=W∘R=(0.26,0.22,0.18,0.61,0.68)。

计算的有效度α=0.49＜0.50，说明最大隶属度原则在此时应用比较低效，故继续采用加权平均原则求出对象隶属等级BT=4.13。最终确定其岩体质量评价等级为Ⅳ级。

重复以上步骤，对所有巷道分段进行了模糊综合评价，结果见表4。

评价结果表明，右2巷道岩体质量整体较差，处于Ⅳ～Ⅴ级。为了验证改进的模糊综合评价法在巷道岩体质量分级中的可靠性和可行性，将分级结果与传统的模糊综合评价法和国标BQ分类法的分级结果进了行对比，结果见表5。

由表5可知：传统的模糊综合评价法根据最大隶属度原则会直接将所有分段的岩体质量归类为Ⅴ级，考虑不够全面且说服力不足，与BQ法的评价结果也存在较大差异。本研究改进的模糊综合评价法对巷道围岩质量的分级结果与BQ法的评价结果更为接近，同时解决了BQ法对抗压强度过于敏感，而弱化其他因素影响力的问题，使得其评价结果更为可靠。