基于随机投影和OMP的大规模稀疏线性回归算法*
2020-08-14祁德涛邹仕祥
祁德涛,杨 健,邹仕祥,郝 琳
(1.陆军工程大学,江苏 南京 210007;2.96037部队55分队,江苏 南京 210007)
0 引言
随着大数据时代的蓬勃发展,互联网技术突飞猛进,网络带宽、数据存储等技术等的提升让各行各业的数据都呈指数式增长,大数据分析与利用逐渐成为各领域角逐的焦点。在当前市场环境下,各行各业对其掌握的数据进行预测具有极高实用价值,大规模稀疏线性回归分析作为数据预测最基本手段也是当前学者们研究的热点。目前稀疏线性回归算法大多是基于梯度下降的算法,其在大规模问题求解上具有局限性。本文研究大规模稀疏线性问题高效求解方案。假设给定数据矩阵及其对应的观测值,其中元素xi∈ℝd表示数据矩阵第i个样本的特征,yi是其对应的观测值。稀疏线性回归要解决的问题是学习稀疏线性函数f(x)=XTβ使得每一个yi都能够被f(x)很好的近似,其问题的核心是求解由模型系数稀疏向量。本文研究数据特征维度大于样本个数的情形,即d>n。
对于稀疏学习领域,解决稀疏向量β求解问题可建模为经典的LASSO问题:

其中,λ为稀疏模型的正则化系数,||●||是向量l2范数。
近年来,很多求解式(1)优化问题方法尝试在非光滑凸优化算法上做出改进,提出了很多高效的优化算法。文献[1]中,作者提出适用于求解非光滑凸优化问题的修正邻近梯度法,算法的特点是采用自适应步长参数,并且该算法的线性收敛性不需要目标函数的强凸性作为前提。文献[2]中,为了解决更为复杂的可分块的凸优化lasso问题,采用分快思想,将目标函数转化为多个凸函数之和,借助邻近算子,利用交替邻近梯度法有效的解决了这一类问题。文献[3]提出了基于同伦策略的近端梯度下降算法,利用迭代策略,将问题转化为求解一系列形如式(1)的子问题。以上算法再解决过程中虽然都能达到一定的收敛速度,但由于其迭代都是以当前梯度为基准,每次迭代过程中对梯度的求解需要计算形如XXTβt的矩阵相乘,其计算量为O(nd),当数据样本与特征数都较大时,迭代运算复杂度过高。
本文以降维为出发点,借助了随机投影算法在大数据应用中的高效降维优势。由于随机矩阵算法在大数据应用中的高效性,现在的随机矩阵算法很多均被应用到了最小二乘[4]和低秩矩阵近似[5]等问题的快速求解上。最近有研究结果表明,相比传统的求解算法(比如,Cholesky分解,QR分解),基于随机矩阵的最小二乘问题近似求解以及矩阵的低秩近似算法的算法复杂度取得明显的降低。
具体的,近几年学者们提出了很多随机矩阵算法[6]用以加速大规模数据数据分析中的相关问题。他们通常通过构建数据矩阵X的低秩近似矩阵缩小原问题的规模,然后通过求解小规模问题获得原问题近似解。目前的随机矩阵算法根据构建随机矩阵的方式,主要分为两大类:基于随机采样的方法和基于随机投影的方法。基于随机采样的方法[7]中,构建的随机矩阵的每一列都是根据特定的概率从原始数据矩阵抽样得来。而基于随机投影的方法[8]中,随机矩阵的列元素都是原始数据矩阵列元素的线性组合。由于随机矩阵算法相对是一个较新的研究内容,在大规模稀疏学习模型训练算法中,暂时还没较多研究成果,最近的研究成果中文献[9]则利用随机投影的办法,结合基于同伦策略的近端梯度下降算法设计了一个复合的稀疏线性回归模型训练算法。利用随机投影首先降低了数据矩阵的规模,在一定程度上提高了算法整体效率。
综上所述,本文设计了一种基于随机投影的加速稀疏线性回归问题求解方法。算法分为两步:首先利用随机投影构建数据矩阵X的低秩近似矩阵其中从而使得梯度计算涉及的矩阵乘法XTXβt近似为WTQTQWβt。通过此方式,计算复杂度由O(nd)简化为O(dk+nk),当k<<min(n,d)时,效率提升非常明显;第二步,通过正交匹配追踪算法,利用最小二乘估计方法迭代地逼近已知支撑集下的稀疏向量。对于K-稀疏向量,OMP算法只需要K次迭代就能找到稀疏向量所有稀疏位置,最优地恢复稀疏向量。
通过上述的分析,本文的贡献主要以下两点:(1)提出利用经典的OMP算法求解稀疏线性回归问题,避免了基于梯度下降之类算法迭代计算梯度高复杂度的问题;(2)结合随机投影与OMP算法,提出面向稀疏线性回归问题的基于随机投影的OMP算法,大幅度提高了大规模稀疏线性回归问题求解效率。
1 基于随机投影的OMP算法
基于当前大规模数据稀疏线性回归算法存在的弊端,本文结合随机矩阵算法在大规模数据分析的优势以及OMP算法的优势,提出基于随机投影的OMP算法。首先利用随机矩阵算法对大规模数据进行k-低秩近似降维,达到减小规模的目的。考虑到本文待解决问题是欠定的,如果采用随机采样的方式,会导致问题更加欠定,因此本文利用随机投影的办法,算法第二步将k-低秩近似降维的数据矩阵和对应的观测值作为输入,利用OMP算法求解稀疏向量β。据目前所知,这是第一次将随机投影算法与OMP算法结合。算法流程如下:
基于随机投影的正交匹配追踪算法
1:输入:数据矩阵x、响应向量y、参数λ0和k
3:采样d×k随机矩阵Z,其中Zij服从正态分布N(0,1)
4:计算矩阵XTZ的QR分解,即XTZ=QR
5:计算x的低秩近似矩阵=(XQ)QT
6:计算稀疏向量β:
7:初始化β0=0
8:fort=0 tok-1 do
9:初始化残差r0=y
11:end for
12:输出β
2 算法理论分析
2.1 矩阵低秩近似的随机投影算法
考虑到本文与最小二乘问题和低秩矩阵近似的随机投影算法关联较大,本节首先介绍随机投影算法在经典最小二乘和低秩矩阵近似问题的原理。
引理2.1 对任意ε,δ∈(0,1)和正整数n,令d为正整数且满足:

定义A为上述随机投影,对于Γ上含有I个点的任意集合I,至少以1-δ的概率,对所有的,都有下述不等式成立,

这就是Johnson-Lindenstrauss引理,引理表明,高维数据能够通过满足一定性质的Lipschitz映射,将其映射到低维空间中,并且能较高概率近似地保持原始数据的几何形状。
针对最小二乘问题中随机投影的应用:


2.2 正交匹配追踪算法
本文第一部分利用随机投影预处理达到了降维的目的,然后利用OMP算法解决稀疏线性回归问题。之前的学者已经证明了OMP算法在压缩感知重构中良好的表现,OMP算法能够快速有效的在有限的步数内最优的恢复感知矩阵,那么基于压缩感知问题和稀疏线性回归的相似性,算法是否也能快速有效的在有限的步数内恢复出稀疏向量。本文的理论推理和实验结果最终证明其是可行的。
OMP算法是一种贪婪算法,贪婪算法是基于l0优化的启发式恢复算法。相比于凸优化算法,它具有简单、快速、高效的特点,其核心思想是贪婪的选取当前匹配测试中最匹配的原子,并在追踪下一次测试前去掉已选择原子带来的影响,直到算法收敛。它主要包括四个关键步骤:匹配测试、贪婪选取、追踪准则和停止准则。匹配追踪(MP)是最简单的贪婪算法,它每次迭代选择最匹配的原子,其追踪准则只是简单地利用相干投影系数不断地逼近稀疏信号,因而收敛速度慢、重构精度差。OMP算法则在追踪时用最小二乘估计的方法逼近已知支撑集下的稀疏信号,而最小二乘是当前支撑集下的正交的最优化估计,从而避免了在下次匹配测试中重复地选择已选择过的原子。对于K-稀疏信号,OMP算法只需要K次迭代就能找到所有的稀疏位置,并最优地恢复出信号。
假设对于K-稀疏向量β,其对应的稀疏支撑集为S={S1,…,SK}∈{1,…,N}和对应的数据矩阵X,由稀疏恢复公式得:


匹配测试是算法的核心,它根据残差与数据矩阵列原子的匹配程度来贪婪的选择稀疏原子,对于第t次选取,匹配测试为:

匹配测试能够准确的选择正确的稀疏位置的保证为|Tt∈S|>>|Tt∉S|。从上式可知,列原子的匹配程度与信号的稀疏度、噪声成分和数据矩阵列原子间的非相干程度有关。如果数据矩阵是N×N正交矩阵,那么原子间相干系数为:

因此在一定的信噪比下,|Tt∈S|>>|Tt∉S|必然成立。其中:

对于稀疏信号的数据矩阵来说。M×N的数据矩阵是冗余的,其列原子并不是正交的,而且具有较小相干系数。为保证匹配测试能够选择正确的稀疏位置,数据矩阵的列原子必须是近似正交的,在感知矩阵良好的非相干性保证下,匹配测试的成功概率随着信号稀疏度和信号噪声能量的增加而不断衰减。因而,对于同一数据矩阵,贪婪算法的恢复性能随着稀疏度的增加和信号信噪比的减小而减少。
本小结最后,对算法进行简要的总结:(1)算法更新过程中严格控制追踪准则避免出现当前最匹配原子地重复选取,对于K-稀疏信号,算法只需要迭代K次就能找到完整的稀疏位置,不再需要步长参数。(2)与PGH算法以及目前流行地基于梯度下降一类地算法相比,本算法更新过程中避免了迭代过程中的梯度计算,同时充分利用了随机投影在大规模数据矩阵的高效性,算法整体效率非常高。
3 实 验
上一节论述了算法的理论可行性。接下来通过实验验证算法的准确性。本文的实验结果将与文献[11]中PGH算法做对比。
PGH算法:当前最优,具有指数收敛速度
实验主要关注如下三点:(1)算法的收敛速度;(2)待解决模型稀疏度与算法迭代次数的的关系;(3)一定噪声水平下算法的收敛效果。
3.1 合成数据集上的实验
数据集:本实验采用合成数据集,具体产生方式如下。数据矩阵X:首先构造一个服从[-1,1]均匀分布的随机矩阵,然后对其进行QR分解。即U=QR,其中,。随后选取Q的前k项得到新矩阵通过该计算得到低秩矩阵最后在低秩矩阵上加上高斯噪声即得数据矩阵X=X0+eX。
稀疏向量β1:根据数据矩阵的特征数d,设置稀疏向量并随即从其中选取s个元素设为1,其余均为零。
响应值y:响应值y通过如下公式计算获得y=XTβ1+ey。其中噪声ey服从高斯随机分布
参数设置:实验中,具体的参数设置如下。对于训练数据集,d=10000,N=5000,k=500,s=25取噪声ex,ey的标准差为1。在PGH算法中,设置λopt=0.001,Lmin=10-9,δ=0.2。在OMP算法中,Lmin=0.001,γ=10-5。
实验目标:通过数据矩阵X和响应值y中恢复稀疏向量β。
算法评估标准:实验需要重点评估学习出来的稀疏向量β的准确性,所以采用相对于最优解的误差||β1-β||2,残差以及运行时间这三个衡量指标。每个实验重复100次,并将均值作为最终结果。
实验结果:如图1、2,展示了噪声水平设置为1时,随着迭代次数的增加,稀疏向量误差、响应值残差的变化情况。图1、2可以看出OMP算法与PGH算法相比,β以越来越快的速度提升质量,残差也相应的以越来越快的速度减小并在较小迭代次数内收敛。图3、4展示了运行时间与稀疏向量误差、观测值残差的关系。明显地发现OMP算法在整体时间效率上有绝对的优势,以更短的时间收敛,同时结合图1、2也说明OMP算法单次迭代效率更高,计算更加简单。

图1 迭代过程中稀疏向量相对误差变化

图2 迭代过程中残差变化

图3 算法运行时间与稀疏向量相对误差关系
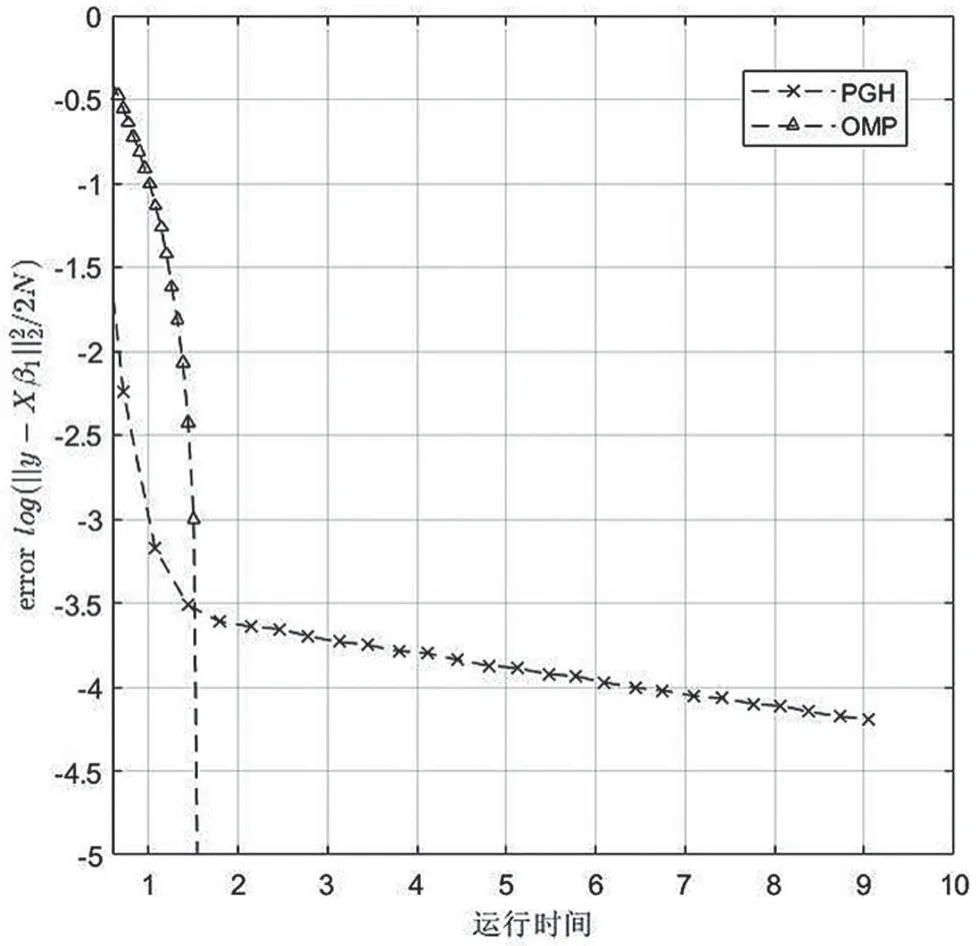
图4 算法运行时间与残差关系
为进一步说明对于K-稀疏向量OMP算法只需要进行K次迭代,实验设置了不同稀疏度的稀疏向量。如下图5展示,证明了OMP算法的迭代次数与稀疏度紧密相关,因此OMP算法求解小稀疏度模型会有更大的速度优势。
最后,为了观察不同噪声水平对两种算法运行结果的影响,实验设计了不同水平的噪声进行比较,相关结果以列表形式展示如表1所示。
实验结果表明对于不同噪声水平,OMP算法始终保持它的效率优势,且其残差和误差均比PGH低,说明其具备一定抗噪能力,收敛效果有保证。
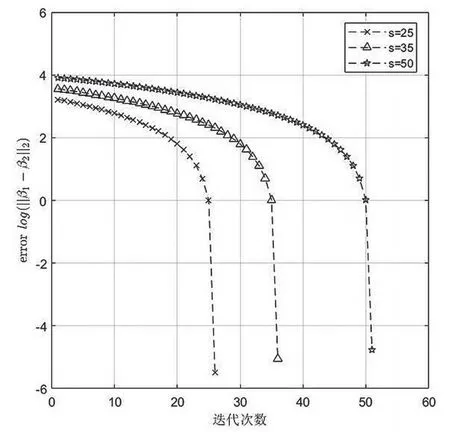
图5 不同稀疏度迭代次数情况
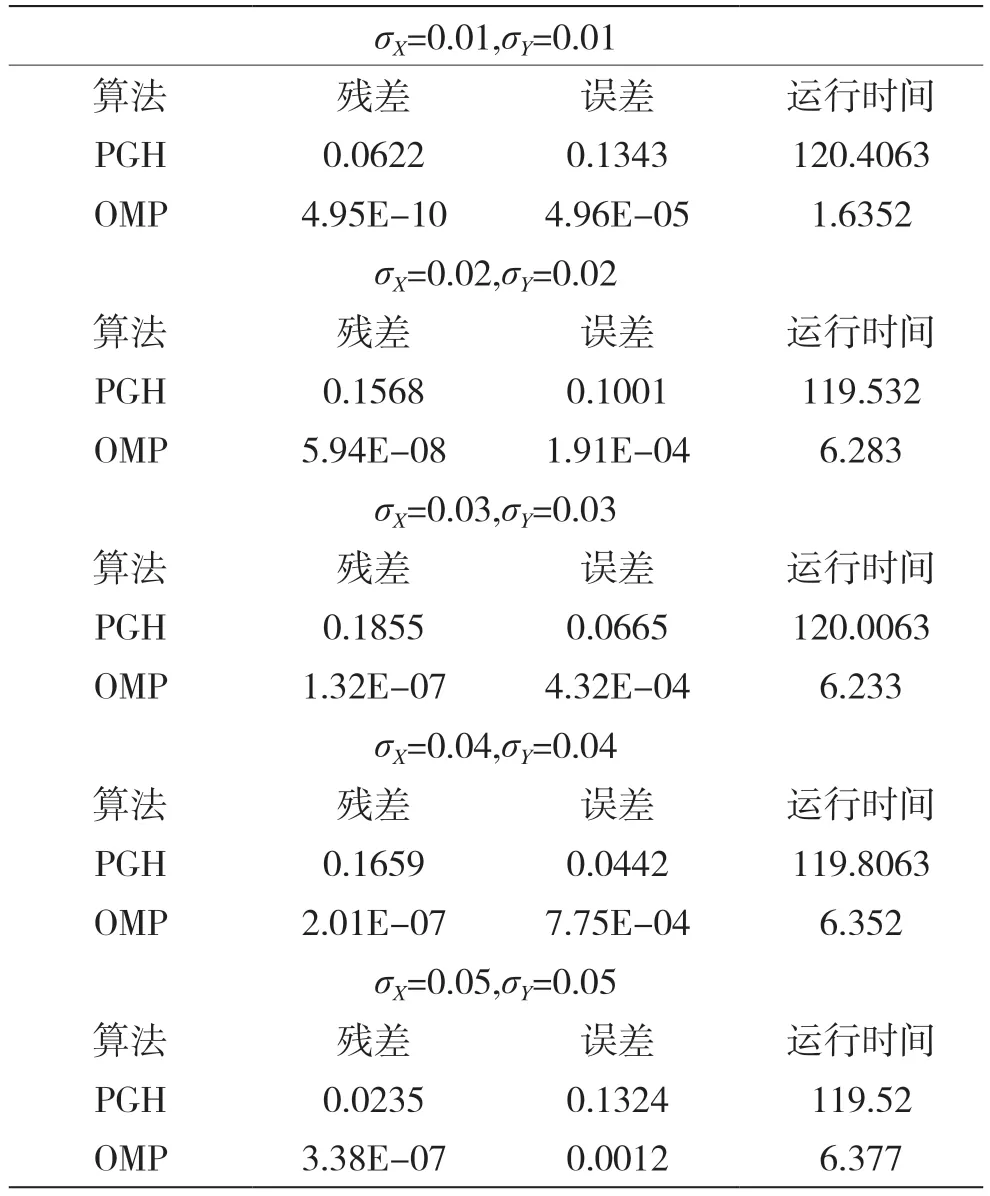
表1 当d=10000,N=5000,k=500时的结果
3.2 实际数据集上的实验
数据集:本文采用Minst数据集进行实验。MNIST数据集是由手写体数字的扫描图片组成的,数据集包含训练样本60 000个和测试样本10 000个。每个样本是一张28×28的图片,其维度是784。本实验,随机地从训练数据集中采集10 000个样本构成数据,然后从测试集中随机地抽取一个样本作为响应值
实验目标:学习出一个稀疏向量β使得y能够被XTβ较好的近似。
参数设置:实验中,k=100,其余参数设置如下。在PGH算法中,λopt=0.001,Lmin=10-9,δ=0.2,Tmax=500。在OMP算法中,Lmin=0.001,γ=10-5。每次实验均重复100次,取均值作为实验结果。
算法评估指标:对于此实验,由于β是未知的,所以采用响应值残差和时间效率作为评估标准,并将实验结果以表格形式展示如表2所示。

表2 当T=500时的结果
实验结论:通过对实验结果的分析,发现OMP算法在时间效率上有绝对的优势。同时,求得的残差与PGH算法相近,说明OMP算法在恢复效果上也是可靠的。
4 结语
本文提出了面向稀疏线性回归的基于随机投影的正交匹配追踪算法。算法首先利用高斯随机投影获得k-低秩近似矩阵,达到降维的目的,降低计算量。然后,提出将正交匹配追踪算法用于求解稀疏线性回归问题。通过理论分析和实验结果对比证明了该算法恢复准确,同时与基于梯度下降一类的算法相比有非常好的时间优势,特别是针对小稀疏度模型问题,算法在恢复效果和恢复效率上都有显著优势。
