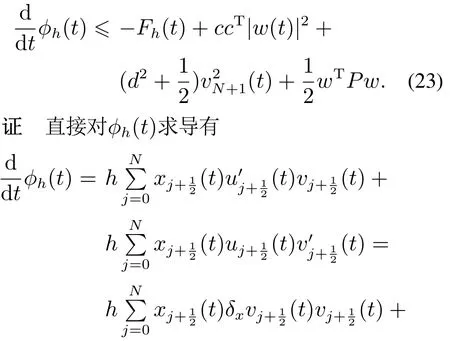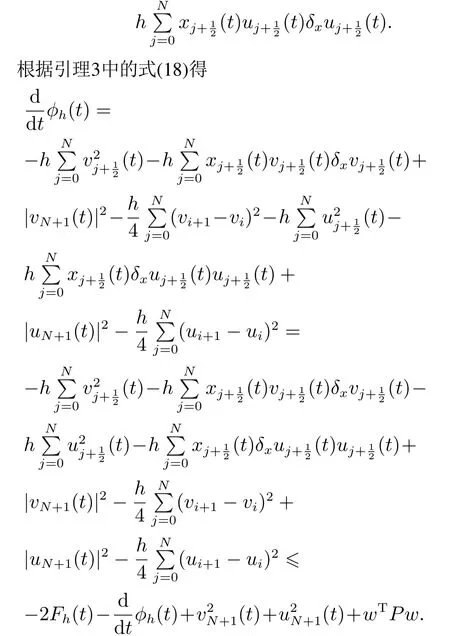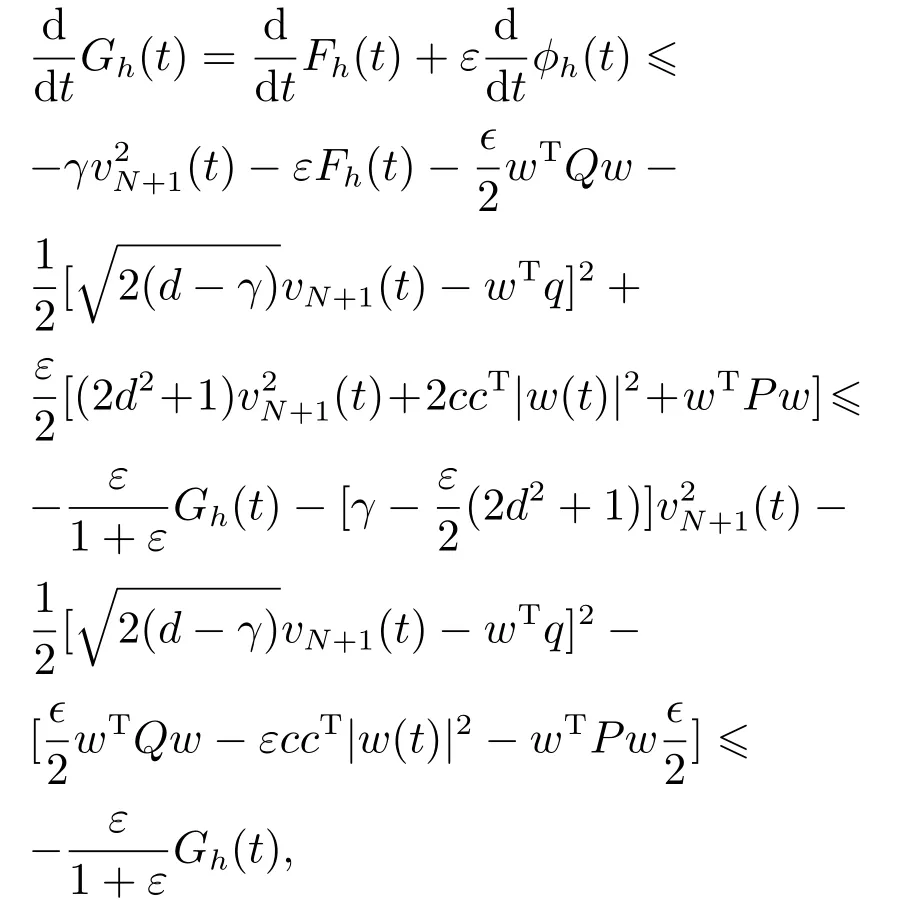具有动态边界阻尼的波方程的降阶型差分半离散化的一致指数稳定性

郑 福,李 艳

(渤海大学数理学院,辽宁锦州 121013)

1 引言

现有一根长度为1的震动的弦,令y(t,x)表示t时刻震动弦在x ∈(0,1)处的位置,弦的一端是固定的,在弦的另一端施加动态边界反馈控制.令为满足z(x)∈L2(0,1),∈L2(0,1),z(x)在闭区间[0,1]上绝对连续和z(0)0的z(x)全体形成的空间.设(y0(x),y1(x))∈(0,1)×L2(0,1)表示弦的初始状态,对∀t0,w(t)∈Rn是控制器的状态.令A ∈Rn×n是常数矩阵,b,c ∈Rn是列向量,d是正常数.则具有动态边界阻尼的震动弦可用如下具有初边值条件的一维波方程描述:

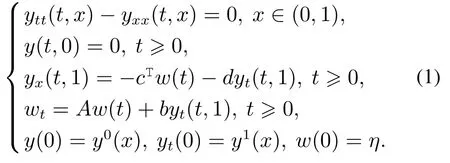
Morg¨ul对系统(1)及其变形进行了详细的研究,研究结果表明在合适的能量空间和条件下,系统(1)是指数稳定的[1–4].但是对于其数值逼近方面的研究几乎没有,然而在过去二、三十年间,如下具有边界阻尼的波方程的数值逼近问题得到广泛而深入的研究.

众所周知,系统(2)在能量空间中的解是存在唯一的且是指数稳定的[5–6],但是用经典的有限差分或者有限元对系统(2)的空间变量进行离散化,这些逼近格式都将产生高频病态伪特征模,致使相应的离散系统关于离散化参数不是一致指数稳定的[7–8].

为了克服传统有限差分和有限元逼近格式在恢复一致指数稳定性方面的不足,学者们做了大量细致而深刻的工作.比如1991年Banks等人引入混合有限元法(指的是用不同的基函数去逼近未知变量y(t,x)和yt(t,x)),利用连续系统类似的验证方法证明离散系统是一致指数稳定的[9].2001年,Fabiano在能量空间中引入与能量内积等价的内积,在新的空间中证明了Galerkin有限元空间半离散逼近格式可一致保持系统的指数稳定性[10].从2003到2007年,Zuazua,Tebou和M¨unch等人通过在有限差分格式中添加消失的数值粘性项,恢复了一维波动方程和二维矩形域中的波动方程的有限差分半离散化逼近的一致指数稳定性[11–13].近期,利用添加数值粘性项法来处理二阶双曲系统的一致稳定性或一致多项式稳定的结果可参看文[14–17].Li 和Sun[18]先将系统(2)看做Port-Hamiltonian系统[19],也就是通过引入合适的中间变量同时对系统(2)的空间变量和时间变量的导数进行降阶处理,然后再用有限差分法对空间变量半离散化,通过引入合适的李雅普诺夫函数和能量乘子法验证离散系统是一致指数稳定的.

受上述工作的启发,本文研究系统(1)的一致指数稳定性问题.通过对上述离散化方法比较后,本文采用的降阶型差分格式,此种方法的优点是不但得到的离散化格式简单,易于被工程技术人员理解和接受,而且完全可以逐步仿照连续系统的验证方法去验证离散系统的一致指数稳定性.研究一致指数稳定性的动机主要来源于两个方面,一是在数值逼近最优控制问题中验证一致指数稳定性是最困难且最重要的一步[9–14];另一个是在可观性的反问题的数值“back and forth”方法中,向前和向后方程的一致指数稳定性起着关键性的作用[20].对于半群或者离散格式的收敛性问题,即:离散系统的解依照某种拓扑收敛到连续系统的解,本文没有给出详细验证,因为这已经超出了控制理论的范畴,有兴趣的读者可从文[13]和文[21]查找相关的收敛性分析.

本文结构如下:在第2节,对系统(1)的指数稳定性给出了一种新的证明方法;在第3节,给出了系统(1)的半离散化逼近系统,利用连续系统的验证方法验证离散系统具有一致指数稳定性.

2 连续系统的指数稳定性

令Re z表示复数z的实部,假设:

H1:矩阵A的所有特征值有负实部;

H2:(A,b)是可控的和(c,A)是可观的;

H3:存在另一常数γ0使得dγ和

在这几个假设下,由此可知系统(2)的传递函数

是正实的,因而由Meyer-Kalman-Yakubovich引理(见文[1]P.1786)可知,对给定任意对称正定矩阵Q ∈Rn×n,存在对称正定矩阵P ∈Rn×n、向量q∈Rn、常数ϵ>0满足

为了达到降阶的目的,将系统(2)看做Port-Hamiltonian 系统的形式,由文[19]中定理9.1.3和例9.2.1可知系统(2)是指数稳定的.对系统(1)可进行同样的处理,为此引入两个中间变量:

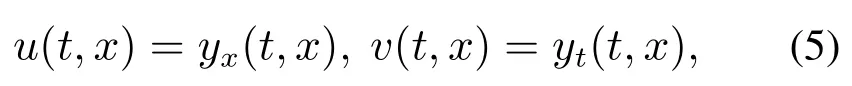
进而得到系统(1)的等价形式,即

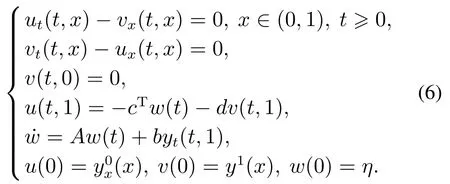
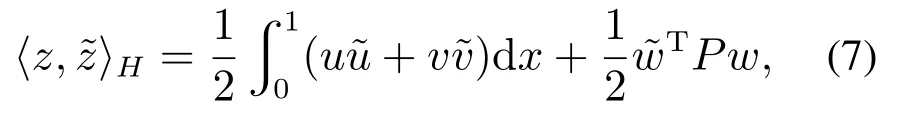
相应于上述内积导出的范数.

这样,可将系统(6)写成抽象微分方程形式:

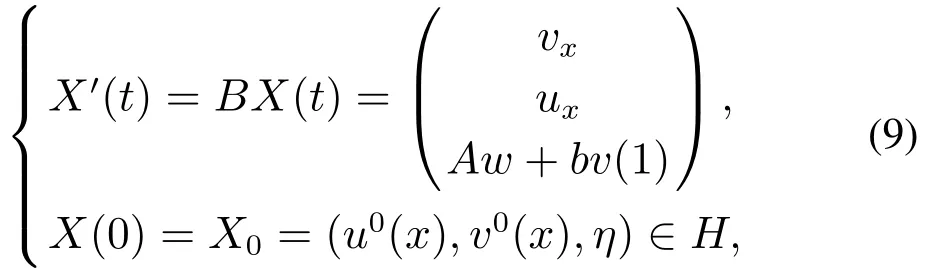
其中算子B的定义域为

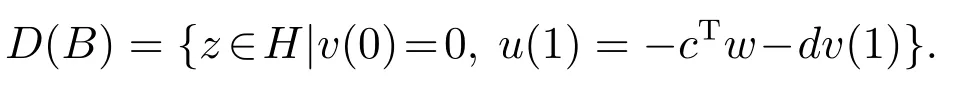
定理1算子B在H上生成的半群是收缩的C0半群.

证很容易看出,算子B是稠定闭算子,由直接计算得

定义域为

所以,B∗也是耗散算子,进而得出由算子B生成的半群T(t)是收缩半群(文[19],定理6.1.8).证毕.

定理1表明系统(6)的唯一解可以由T(t)X0给出,但是,为了得到系统(6)的指数稳定性,构造Lyapunov函数:G(t)F(t)+εϕ(t),其中ϕ(t)<ε<1是可以自由选取的参数.直接利用Cauchy不等式和三角不等式得如下引理.

引理1Lyapunov 函数G(t)等价于能量F(t),即

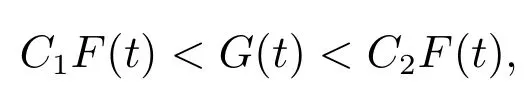
其中:C11 −ε,C21+ε.

引理2辅助函数ϕ(t)满足

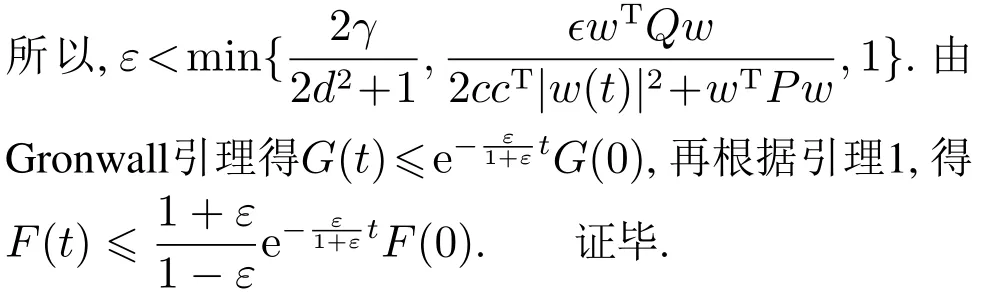
3 离散化系统的一致指数稳定性

在构造系统(6)的有限差分空间半离散化之前,先引入一些符号,对任意的N ∈N+,将区间[0,1]进行等距划分:

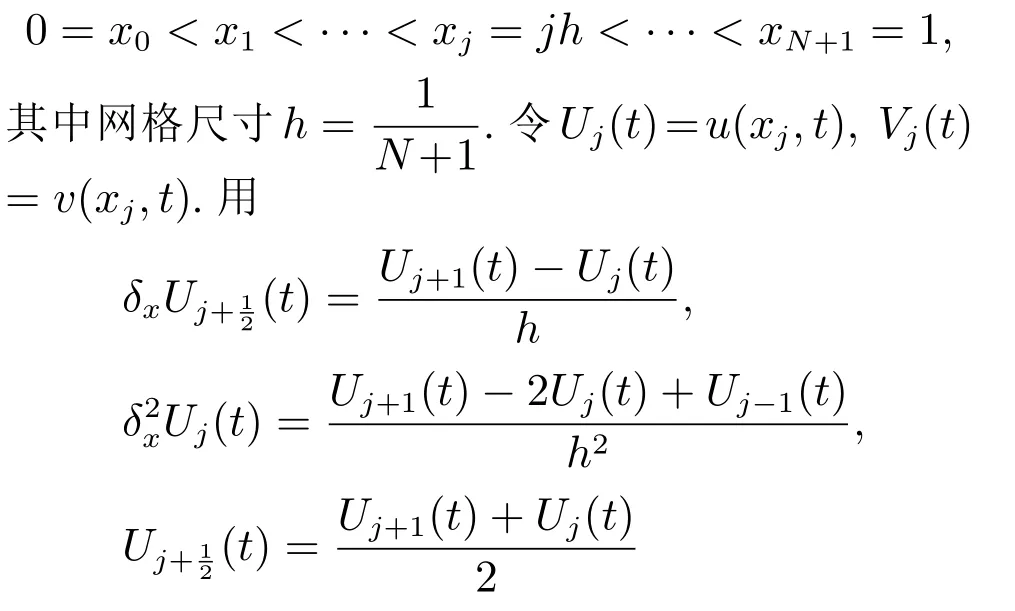
分别表示一阶差分算子、二阶差分算子和平均算子.

这样就可用有限差分方法对系统(6)进行离散化,由于系统(6)的第1个方程在是有意义的,即

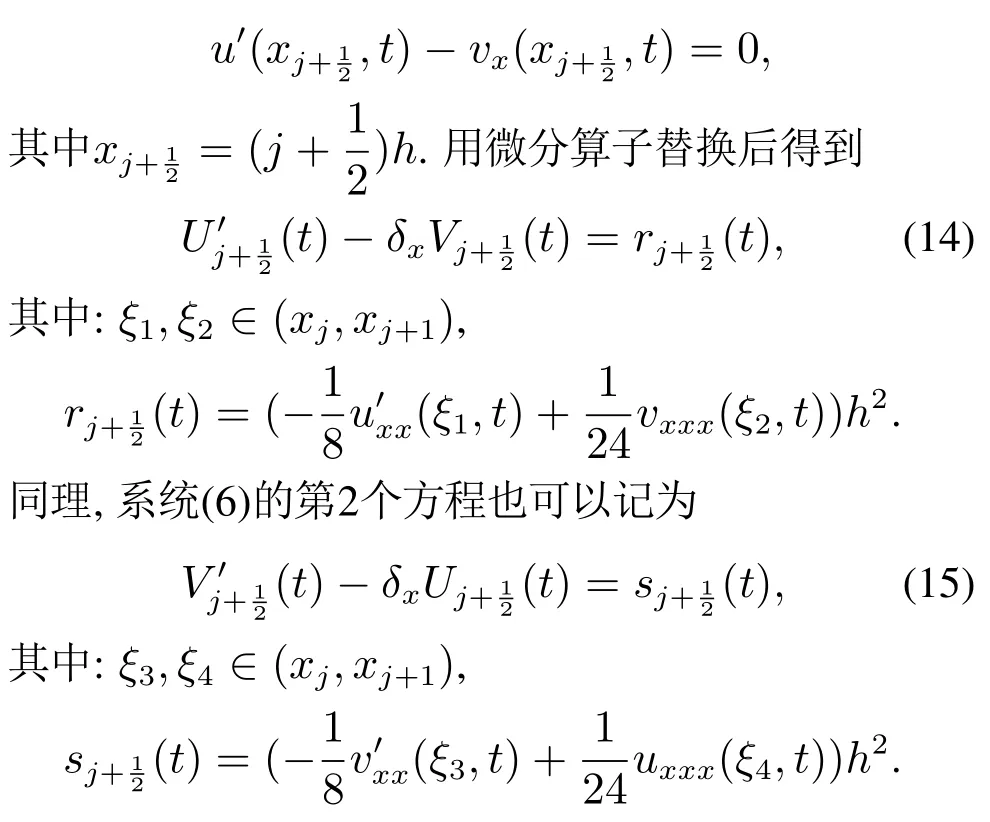
忽略方程(14)和(15)中的无穷小项,并分别用uj(t)和vj(t)代替Uj(t)和Vj(t),得到系统(6)的有限差分空间半离散化形式:

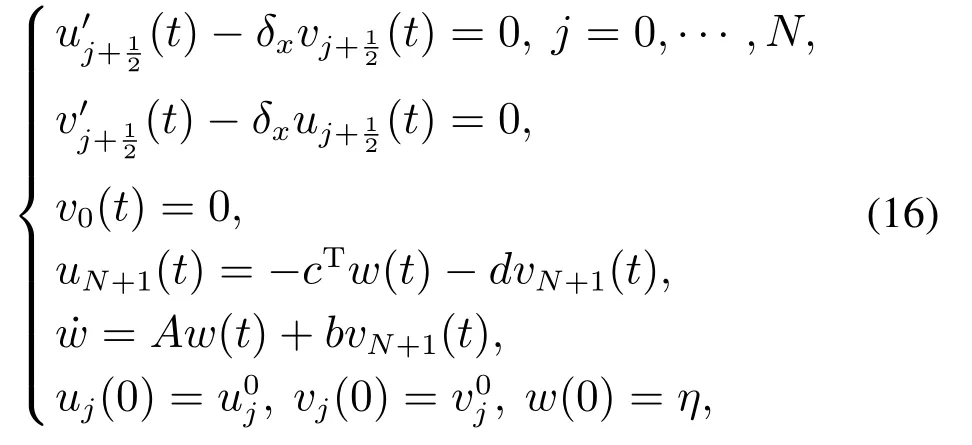
根据上述引入的记号和简单计算可得如下引理[18]:

引理3对任意的{Uj}j,{Vj}j,{Wj}j,有

有限差分系统(16)的离散能量记为

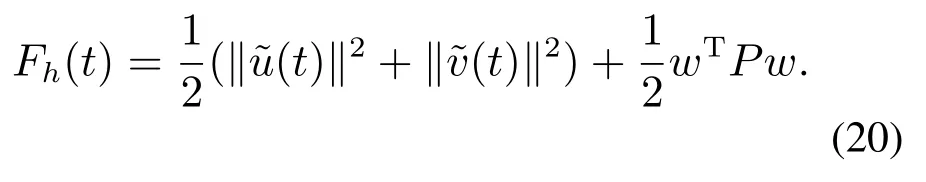
这里的Fh(t)是连续能量F(t)的有限差分半离散化形式.因而有如下定义:

定义1若存在与t和h无关的两个正数M和η使得

则称系统(16)是一致指数稳定的.

接下来用上节的方法验证离散化系统(16)的一致指数稳定性.

由引理3中的式(17)得

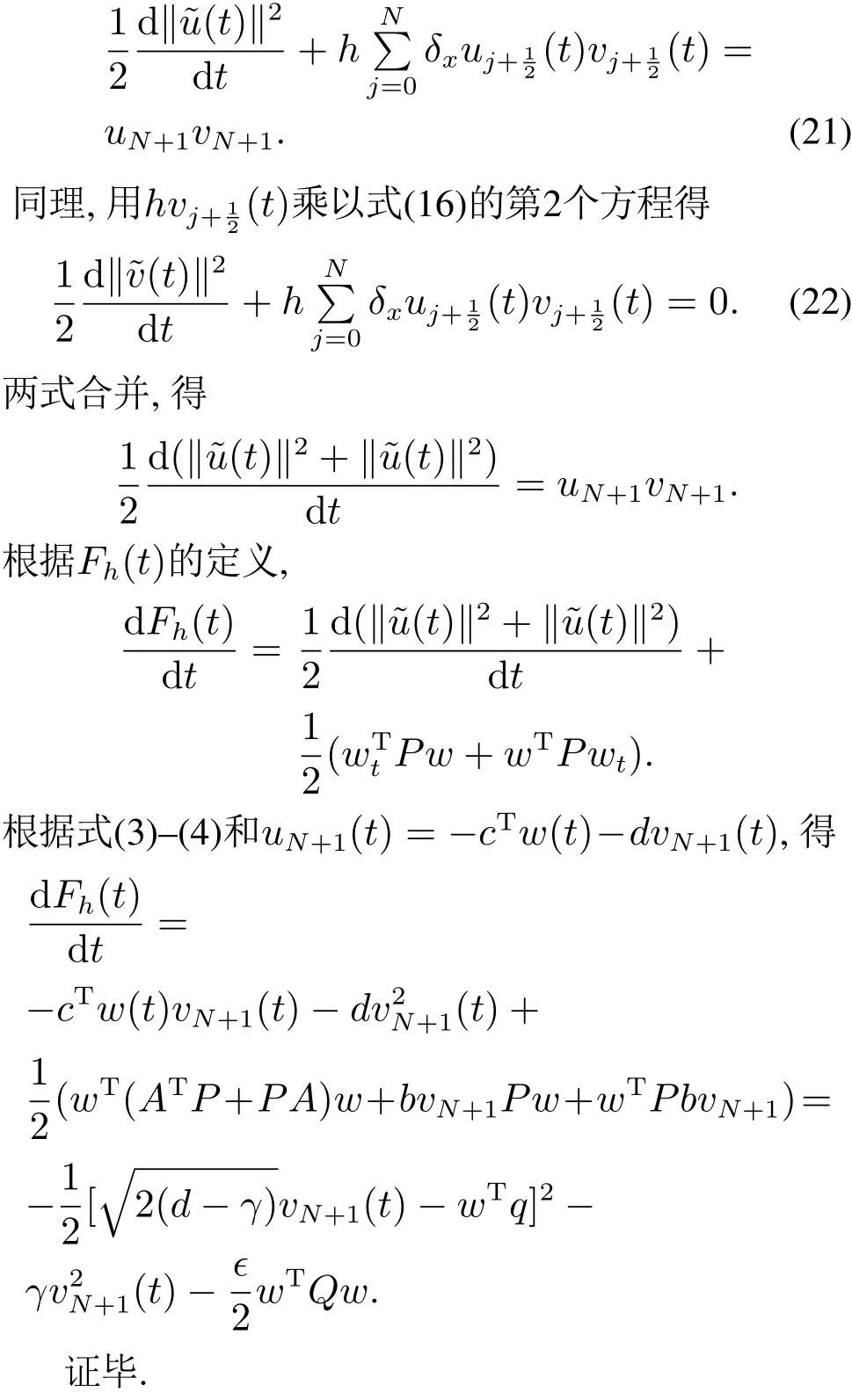
引理4表明系统的离散能量随着时间的增加而减少.与连续情形类似,为了得到离散系统能量的一致指数衰减率,需要构造如下Lyapunov函数: Gh(t)Fh(t)+εϕh(t), 0<ε<1,其中辅助函数ϕh(t)满足

与引理1类似,也有如下引理:

引理5Lyapunov函数Gh(t)等价于能量Fh(t),即C1Fh(t)

引理6辅助函数ϕh(t)满足

由于uN+1(t)−cTw(t)−dvN+1(t),所以有2ccTw2(t)+将其代入上述不等式即可得到式(23).证毕.

定理3系统(16)是一致指数稳定的.

证由引理4和引理6有

其中