波纹辊轧机辊系主共振时滞反馈控制

和东平,王 涛,任忠凯,冯 光,刘元铭

(太原理工大学机械与运载工程学院,山西太原 030024)

1 引言

铜/铝复合板、钢/铝复合板等层状双金属复合材料在保持基材特性的同时还具有“互补效应”,经过适当的配比组合可具有优异的综合性能,是国民经济建设中急需的一类重要新材料[1].金属复合板轧制生产的传统工艺是轧机的上下工作辊都分别采用平辊轧制实现两种金属的横向与纵向延伸,但是在实际的生产中,由于上下两种金属的延伸率不一样,很容易造成金属大曲率翘曲,不能连续化生产(如图1所示).金属层状复合板波纹辊轧制技术是一项变革性技术(如图2所示),可以促进异种材料更好的实现冶金结合,提高结合强度,实现连续化生产.通过波纹辊轧制铜铝复合板的实验表明:铜铝复合板界面处的晶粒得到明显细化;铝侧晶粒细化程度明显高于铜侧;相同等效压下率下,波纹轧后拉伸过程中界面结合良好,界面处存在韧窝[2].但是,波纹辊的辊型曲线为余弦函数曲线,在复合板的轧制过程中,轧制界面的非线性阻尼以及上下辊系之间的非线性刚度都可能导致上下辊之间主共振等参激振动的发生,造成辊缝的波动,从而影响复合板的生产质量和降低零部件的在线服役时间.

图1 平辊轧制翘曲现象Fig.1 Warping phenomenon of flat roll

图2 波纹辊轧制示意图Fig.2 Rolling diagram of corrugated roll

轧机辊系振动的现象在实际生产中普遍存在,是非线性动力学研究的重要领域之一.常常表现为“幽灵”式多态耦合振动,主要包含轧辊的垂直振动、水平振动、轴向窜动、带钢的横向和纵向振动、主传动系统的扭转振动和轴向振动等,不仅对轧件表面的粗糙度、轧制精度产生不利影响,严重的甚至造成设备的损坏和人员的伤亡[3–6].国内外的许多专家学者针对轧机的振动及控制方面做了大量的研究.Panjkovi V等认为负载钢材的规格和轧辊表面长期工作形成的表面氧化都是引起辊缝摩擦系数变化的原因,进而提出轧机辊缝的摩擦环境的变化是造成轧机系统颤振的一个原因[7].Kapil S等考虑移动板带振动导致的轧辊与轧件间的非线性参激特性,建立了一个单自由度的轧机非线性参激振动模型,并得到轧机振动的不稳定区域及幅频振动特性[8].Younes M A等将轧件等效为具有线性刚度的弹性零件,基于线性振动理论建立了轧机机座的线性垂振模型[9].Maccari A等研究了外激励下的Van der Pol振子在状态反馈时滞控制下如何通过适当的时间延迟和反馈增益来对振动控制和抑振[10].闫晓强通过对热连轧机的研究,发现轧机存在扭垂耦合振动、机电耦合振动和液机耦合振动现象,确定轧机振动的性质为机电液多态耦合振动[11].彭荣荣等建立了动态轧制力下的四辊冷连轧机非线性振动动力学模型,运用多尺度法求解得到了系统的超谐波共振和亚谐波共振[12].侯东晓等考虑冷轧机轧辊在垂直方向上振动位移动态变化影响,建立了一种动态轧制力模型[13].钱长照等对含有两个时滞参数、受简谐激励作用下的Vander Pol-Duffing方程进行了研究,着重分析了时滞参数对该类参数激励的主共振的分岔响应控制[14].刘灿昌等以衰减率为振动控制参数优化目标,以非线性振动系统振动稳定条件、幅值最值、最优时滞为约束条件,利用最优化方法计算获得最佳线性、非线性反馈控制参数[15].尚慧琳等利用Melnikov函数法获得时滞速度反馈控制相对转动系统产生混沌和安全域分岔的临界激励,在正的反馈增益系数下,时滞速度反馈能够有效地用于控制相对转动系统的混沌运动[16].赵艳影等通过对时滞状态反馈控制自参数动力吸振器减振系统的研究,发现在时滞的调节区间内存在一个时滞的“最大减振点”,能够在该反馈增益系数下最大程度地减小主系统的振动[17].到目前为止,国内外对轧机振动的研究已取得了一定的成绩,但是影响轧机振动的因素较多,涉及到振动理论、轧制理论、故障诊断理论等几大领域的交叉融合.波纹辊轧机是一个多变量、强耦合、非线性、多约束、时变性的系统,波纹辊轧机的振动问题影响着产品的质量和零部件的在线使用寿命,但是,目前还没有学者针对波纹辊轧机辊系的振动特性展开相关研究.

本文基于金属复合板波纹辊轧制成形技术,考虑了波纹辊轧机波纹界面间的非线性阻尼和非线性刚度,建立了波纹辊轧机两自由度垂直非线性主共振数学模型.利用奇异值理论和相平面法讨论了波纹辊轧机辊系自治下的稳定性,运用多尺度法求解了波纹辊轧机辊系在波纹界面激励下的主共振的解析近似解和幅频特性方程.分析了非线性刚度系数、非线性阻尼系数、系统阻尼系数、轧制力的幅值等参数对主共振的影响.设计了线性和非线性复合作用的时滞反馈控制器来对波纹辊系的稳态响应进行控制,并且通过数值仿真证明了当线性增益g1>0、非线性增益g2>0时,时滞反馈控制器可以对波纹辊轧机辊系的主共振现象进行合理的控制,避免分岔现象的发生,为抑制波纹辊轧机的辊系振动和升级改造提供了一定的理论指导.

2 波纹辊轧机辊系主共振数学模型

考虑波纹辊轧制界面的非线性阻尼以及波纹辊之间的非线性刚度,波纹辊轧机辊系可以简化为两自由度垂直非线性参激振动模型如图3所示.

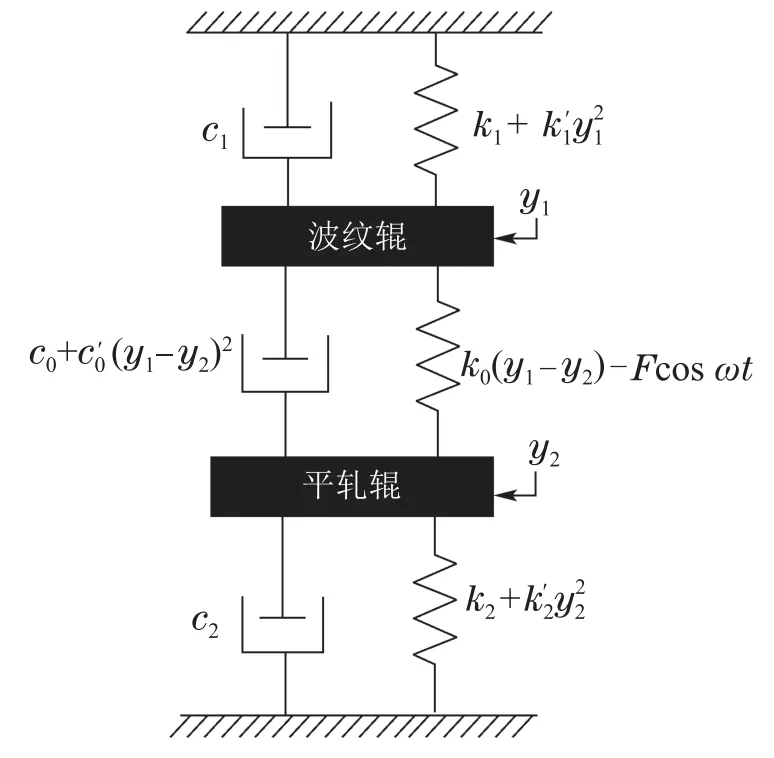
图3 波纹辊系参激振动数学模型Fig.3 Parametrically excited vibration mathematical model of corrugated roll

图3中,m1代表波纹辊的等效质量,m2代表平轧辊的等效质量,k1是波纹辊与机架之间的刚度,k2是平轧辊与机架之间的刚度,k0表示波纹辊轧机稳态过程中刚度的均值,F cos wt近似为轧制过程中的轧制力,c1为波纹辊与机架间的阻尼平均值,c2为平轧辊与机架间的阻尼平均值.考虑到波纹辊轧机的非线性阻尼和刚度特性,将Vanderpol振子定义为波纹辊轧机在轧制过程中由于辊型曲线的影响导致的上下工作辊之间的非线性阻尼,将Duffing振子k+k′y2定义为波纹辊系和机架间的非线性刚度项.波纹辊轧机主共振方程表示为

在波纹辊轧制复合板的过程中,上下辊系具有近似对称性.因此令m1m2,y1−y2,则式(1)可以简化为

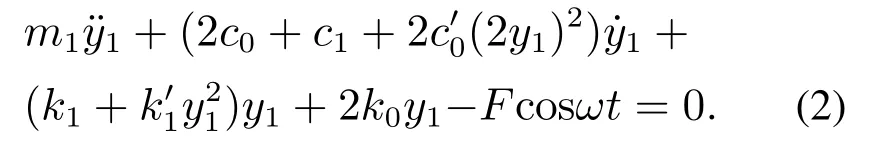
将上式无量纲化,其中y的导数是对时间τ的求导,为了习惯表达,仍用t代替τ.令

则两自由度非线性振动微分方程可以简化为

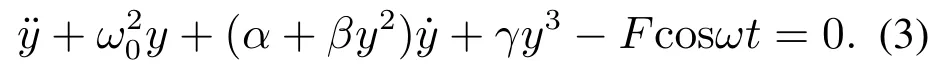
假设ε为小参数,将式(3)的非线性项冠以小参数ε,则有

3 波纹辊轧机辊系稳定性分析

波纹辊辊系的稳定性对复合板的生产质量有着重要的影响.基于奇异值理论和相平面法,对波纹辊辊系在自治状态下的稳定性进行分析[18],非线性刚度系数γ约定为正.

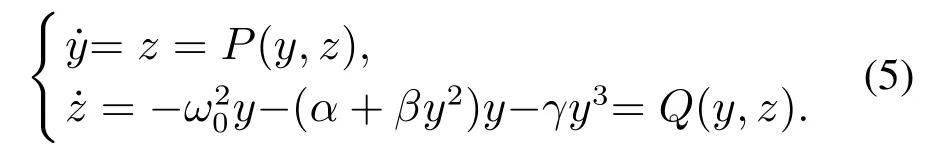
得到波纹辊轧机自治系统的雅克比矩阵为

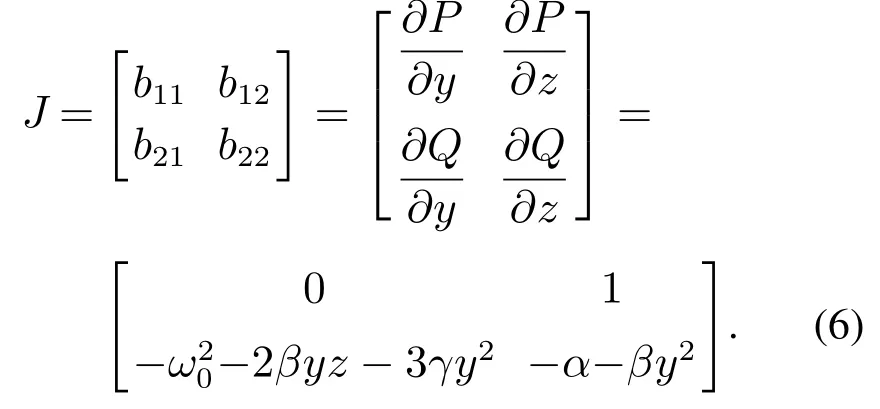
由式(5)可知,当γ >0时,自治系统的奇点为(0,0),带入式(6)得到

由奇异值理论和相平面法可知[19]

1)特征值均为负实数,奇点是稳定结点;

2)特征值均为正实数,奇点是不稳定结点;

3)特征值表示正负号相异的两个实数,奇点是鞍点;

4)特征值为实部为负的复数,奇点是稳定焦点;

5)特征值为实部为正的复数,奇点是不稳定焦点;

6)特征值为共轭的纯虚数,奇点称为中心点.

针对ω0和α分别取不同值的分析系统的运动状态,曲线轨迹如图4–10.

图4 ω0=1,α=6时的动态特性响应图Fig.4 Dynamic response diagrams and phase diagrams when ω0=1,α=6

图5 ω0=1,α=2时的动态特性响应图Fig.5 Dynamic response diagrams and phase diagrams when ω0=1,α=2

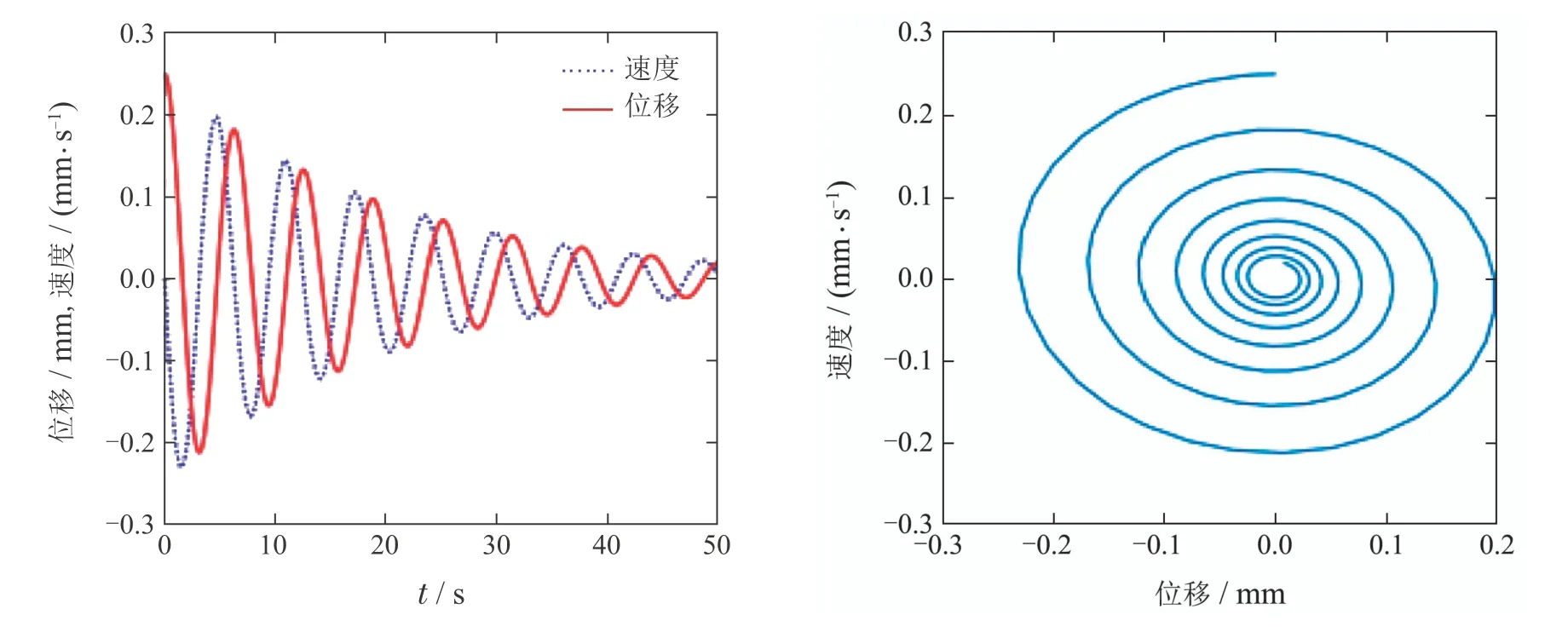
图6 ω0=1,α=1时的动态特性响应图Fig.6 Dynamic response diagrams and phase diagrams when ω0=1,α=1

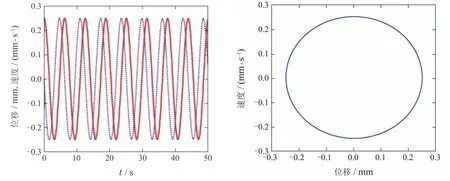
图7 ω0=1,α=0时的动态特性响应图Fig.7 Dynamic response diagrams and phase diagrams when ω0=1,α=0

图8 ω0=1,α=−1时的动态特性响应图Fig.8 Dynamic response diagrams and phase diagrams when ω0=1,α=−1

图9 ω0=1,α=−2时的动态特性响应图Fig.9 Dynamic response diagrams and phase diagrams when ω0=1,α=−2

1)当ω0>0,α>2ω0时,奇点是鞍点,由图4中相轨迹曲线可知系统渐进稳定.

2)当ω0>0,α2ω0时,奇点为稳定结点,由图5中相轨迹曲线可知系统渐进稳定.

3)当ω0>0,0<α<2ω0时,奇点为稳定焦点,由图6中相轨迹曲线可知系统渐进稳定. α的减小会降低波纹辊系的抗干扰性能.

4)当ω0>0,α0时,奇点为中心点,系统处于无阻尼运动状态,图7中相轨迹曲线为封闭的圆.

5)当ω0>0,−2ω0<α<0时,奇点为不稳定焦点,图8中相轨迹曲线以震荡方式“卷离”平衡点,并产生极限环.

6)当ω0>0,α−2ω0时,奇点为不稳定结点,由图9中相轨迹曲线可知系统逐渐发散直至产生极限环,并可能导致系统的振荡失稳.

7)当ω0>0,α<−2ω0时,奇点为鞍点,由图10中相轨迹曲线可知系统逐渐发散直至产生极限环,并可能导致系统的振荡失稳.

图10 ω0=1,α=−6时的动态特性响应图Fig.10 Dynamic response diagrams and phase diagrams when ω0=1,α=−6

4 波纹辊轧机辊系主共振特性分析

波纹辊轧机辊系振动是一个非线性系统,在轧制的过程中可能导致多种共振现象,如:内共振、主参数共振、倍共振.下面主要对波纹辊的轧制力的激振频率ω接近固有频率ω0时的主参数共振进行分析[20–24].

本文采用多尺度法对波纹辊轧机的参激振动进行分析.引入表示不同尺度的时间变量Tnεnt,其中n0,1,2,···,并把它们看成独立的自变量,而X为这些自变量的ε和t的函数,即

其中m为小参数的最高阶次,取决于计算的精度要求.

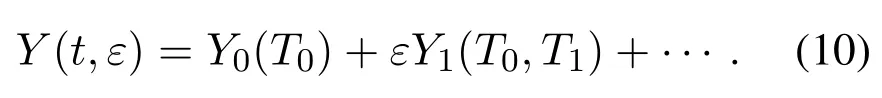
将不同尺度的时间变量视为独立变量,则X(t,ε)成为m个独立时间变量的函数,对时间的微分可利用复合函数微分式按ε的幂次展开,得到

其中Dn(n0,1,2,···,m)为偏微分算子,定义

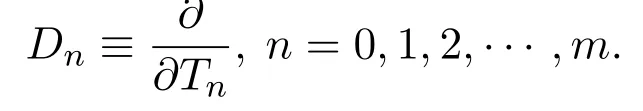
假设ζ为频率调制参数.讨论波纹辊轧制力的激振频率ω 接近波纹辊轧机固有频率ω0时[15–16],令

将式(10)–(12)代入式(4),展开后令两边ε的同次幂系数相等,得到各阶近似方程

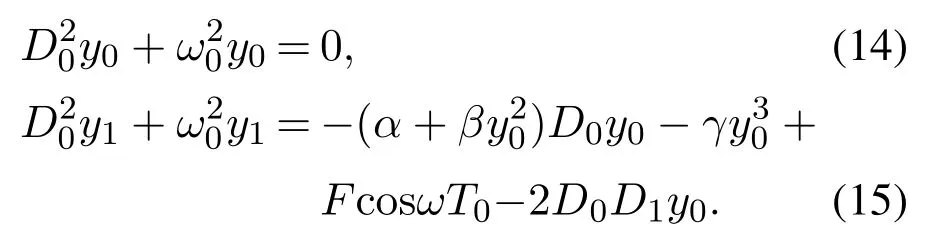
设零次近似方程(14)的解为

其中∆代表前一项的共轭复数.

将式(16)代入式(15),得到

为了避免出现久期项,必须使函数B满足

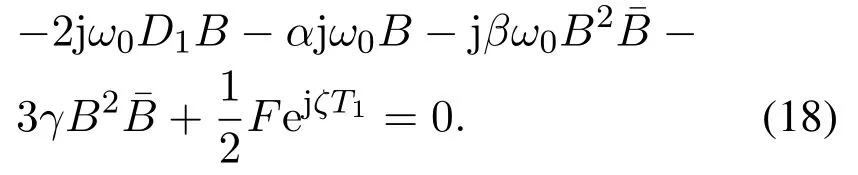
将B表示成复数形式,令

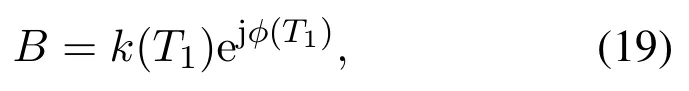
将式(19)代入式(18),分离实部与虚部,得到

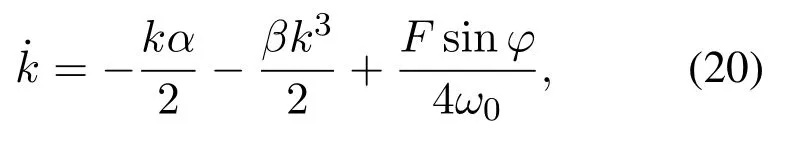
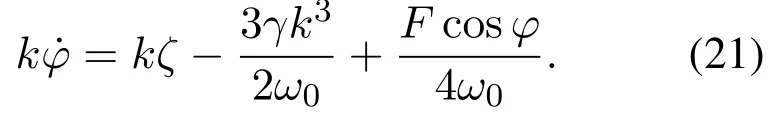
化简式(20)–(21)可得主共振一阶近似解

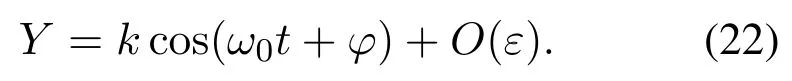
改变波纹辊轧机的非线性刚度系数γ(0.1,0.3,0.6,0.9),非线性阻尼系数β(0.01,0.03,0.06,0.09),系统阻尼系数α(0.02,0.04,0.06,0.08),轧制力的幅值F(0.1,0.3,0.6,0.9),可得不同的主共振幅频特性曲线(扰动频率ζ与振幅k之间的关系),如图11所示.

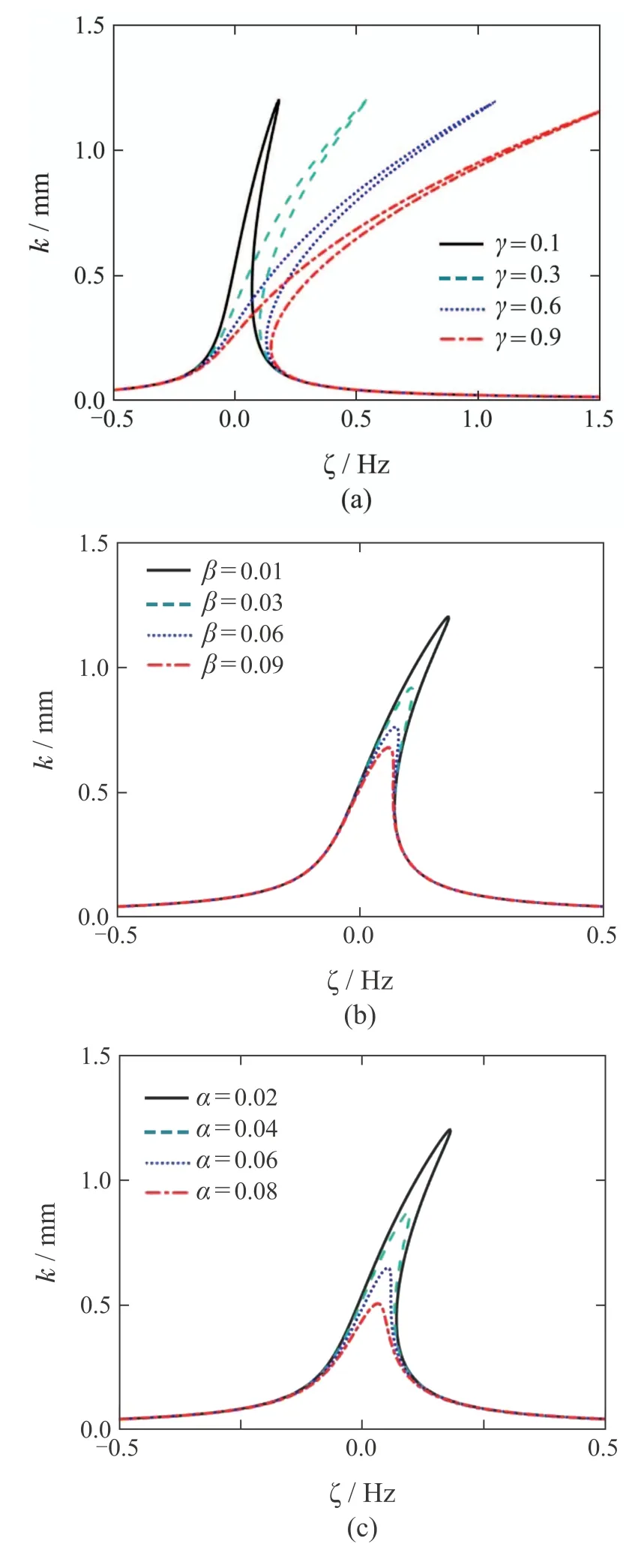
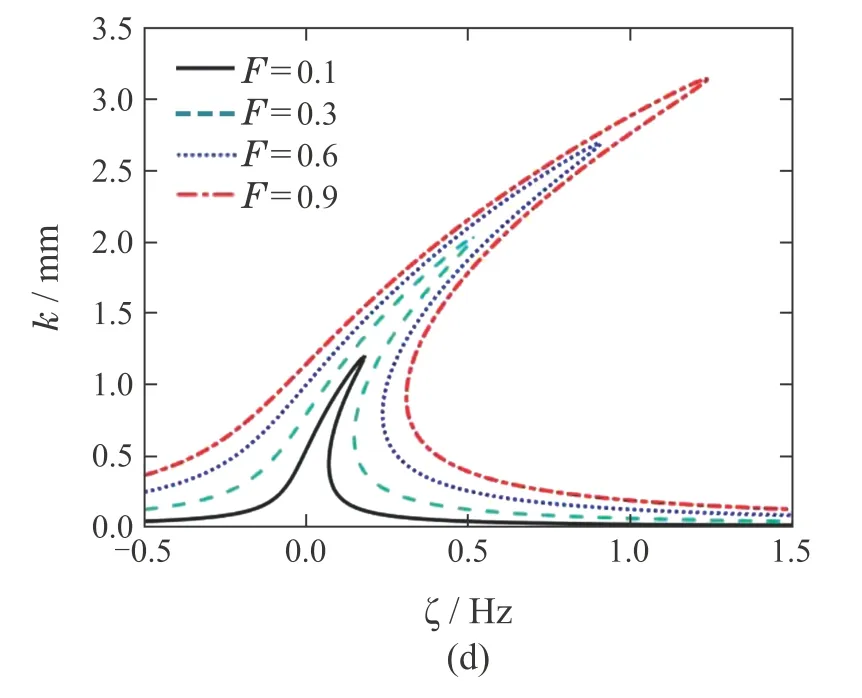
图11 不同参数对主共振幅频特性曲线的影响Fig.11 The amplitude-frequency characteristic curve of principal resonance with different parameters

如图11(a)所示,随着非线性刚度系数γ的增大,曲线右移而且弯曲程度增大.当扰动频率从负值到正值变化的时候,幅值出现跳跃,引起系统的振荡.如图11(b)所示,随着非线性阻尼系数β的增大,振幅减小且共振域减小.如图11(c)所示,随着系统阻尼系数α的增大,振幅减小且共振域减小.非线性阻尼系数β和系统阻尼系数α的变化不影响频响曲线的弯曲程度.如图11(d)所示,随着轧制力的幅值F的增大,系统的振幅和共振区域明显增大.因此,在波纹辊设计的过程中,应该合理优化波纹曲线来避免和减小轧制力幅值对主共振的影响.

5 波纹辊轧机辊系主共振时滞控制

波纹辊轧机辊系是一个高度非线性滞后系统,在复合板的轧制过程中,轧件的弹塑性变形过程是一种具有时滞特性的非线性变形过程.基于波纹界面的作用,轧制力的波动会使轧件处在加载和卸荷的交替中,处在塑性变形阶段的轧件的屈服极限不断变化、使得加载曲线和卸荷曲线不重合,从而会导致接触界面的非线性阻尼和非线性刚度表现出时滞特性.

时滞反馈控制方法是研究非线性系统分岔控制的有效方法之一.通过设计一种线性和非线性时滞联合作用下的反馈控制器[24]来对波纹辊轧机辊系的主共振响应进行控制,从而消除波纹辊轧机辊系的跳跃、滞后现象.设含有线性和非线性时滞联合作用的反馈控制器如下:

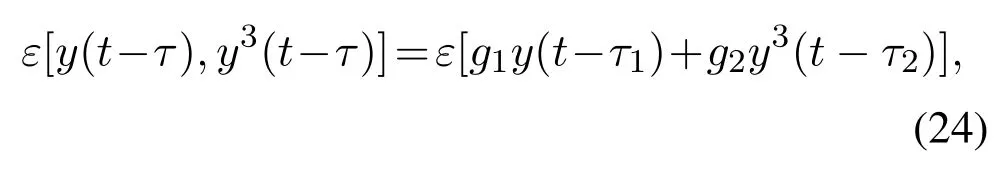
则式(4)可以写成如下形式:

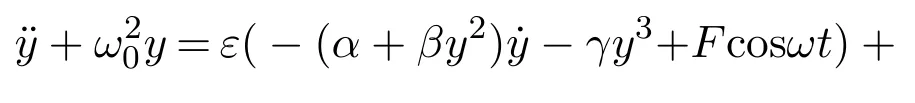
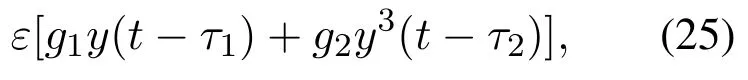
其中: τ1和τ2为时滞参数,g1为线性反馈增益,g2为非线性反馈增益.如果g1和g2为零,则系统为无控制系统.

仍采用多尺度法对改进后的方程(25)进行分析.将式(10)–(12)带入式(25),展开后令两边ε的同次幂系数相等,得到各阶近似方程

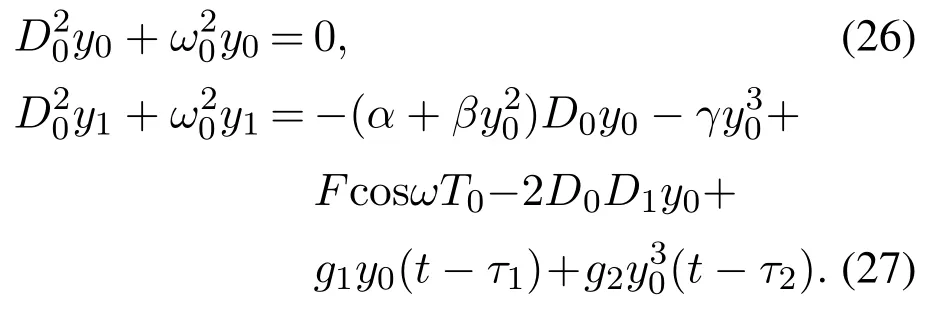
设零次近似方程(26)的解为

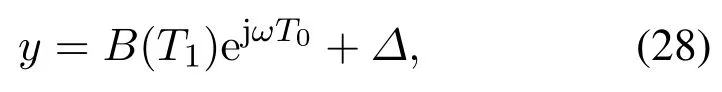
其中∆代表前一项的共轭复数.

将式(28)代入式(27),得到

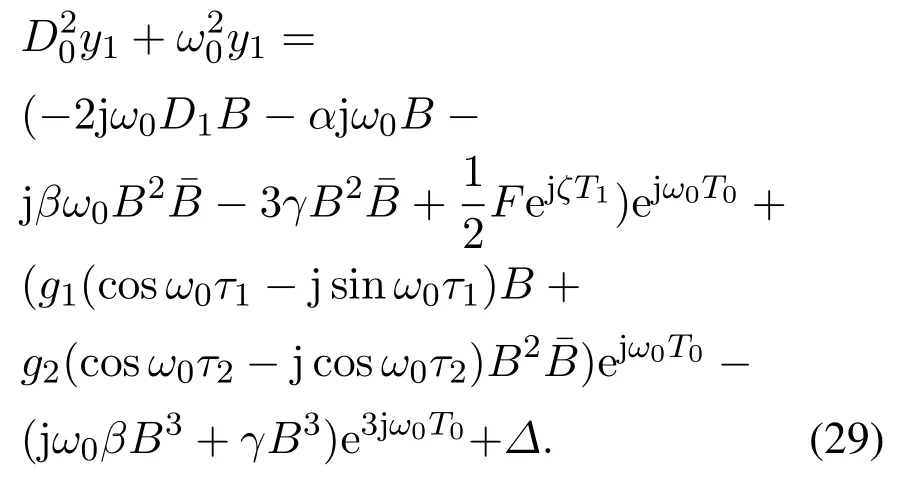
为了避免y1出现久期项须满足

将B表示成复数形式,令

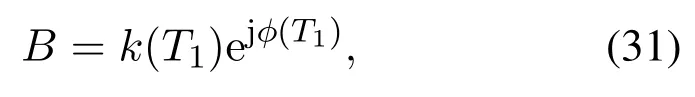
将式(31)代入式(30),分离实部与虚部,得到

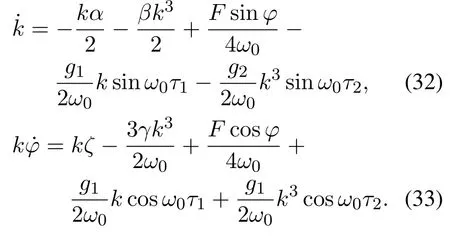
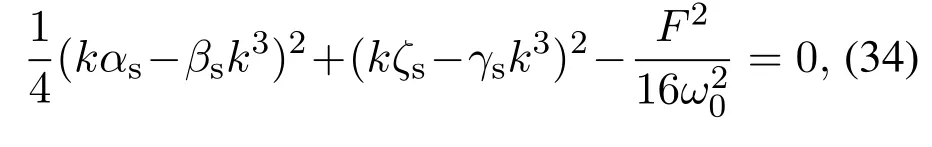
其中:

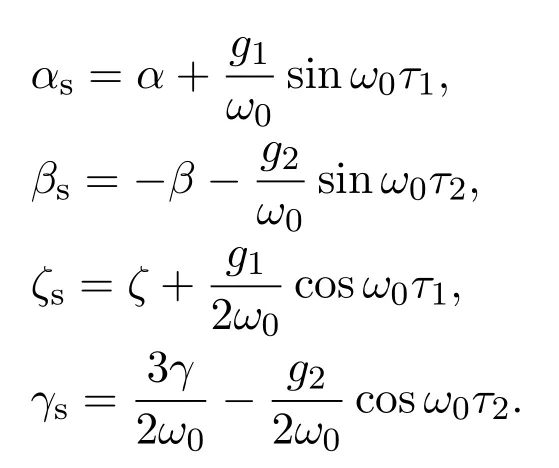
如图12所示,没有反馈控制时,主共振幅频特性曲线存在分岔现象.通过适当的调节时滞量(τ1,τ2)和增益系数(g1,g2)可以达到对主共振幅值和共振区域的控制,减小主共振分岔.通过对比发现同时调节时滞量(τ1,τ2)和增益系数(g1,g2)的控制效果优于单独分别调节线性反馈增益g1和非线性反馈增益g2的控制效果.其中,非线性刚度系数γ0.1,非线性阻尼系数β0.01,系统阻尼系数α0.02,轧制力的幅值F0.1.

图12 主共振时滞控制曲线Fig.12 The time delay control curve of principal resonance

如图13(a)所示,随着线性增益g1和非线性增益g2的逐渐增大,系统的振幅逐渐减小且共振域逐渐减小,消除了曲线分岔.以反馈控制增益作为控制参数时,同时增大线性和非线性反馈控制增益,可以使系统的主共振现象得到合理的控制.图13(b)可以看出,随着时滞参数τ1和τ2的逐渐增大,系统的振幅逐渐减小且共振域逐渐减小,但是调节时滞参数不影响曲线的弯曲程度.通过两幅图可以发现,以反馈控制增益作为控制对象的控制效果优于以时滞参数作为控制对象的控制效果.图13(c)可以看出,当线性增益g1<0和非线性增益g2<0时,不能消除曲线分岔,主共振现象得不到合理的控制.利用线性和非线性复合作用的时滞反馈控制器对波纹辊系的主共振进行控制时,线性增益g1>0,非线性增益g2>0.

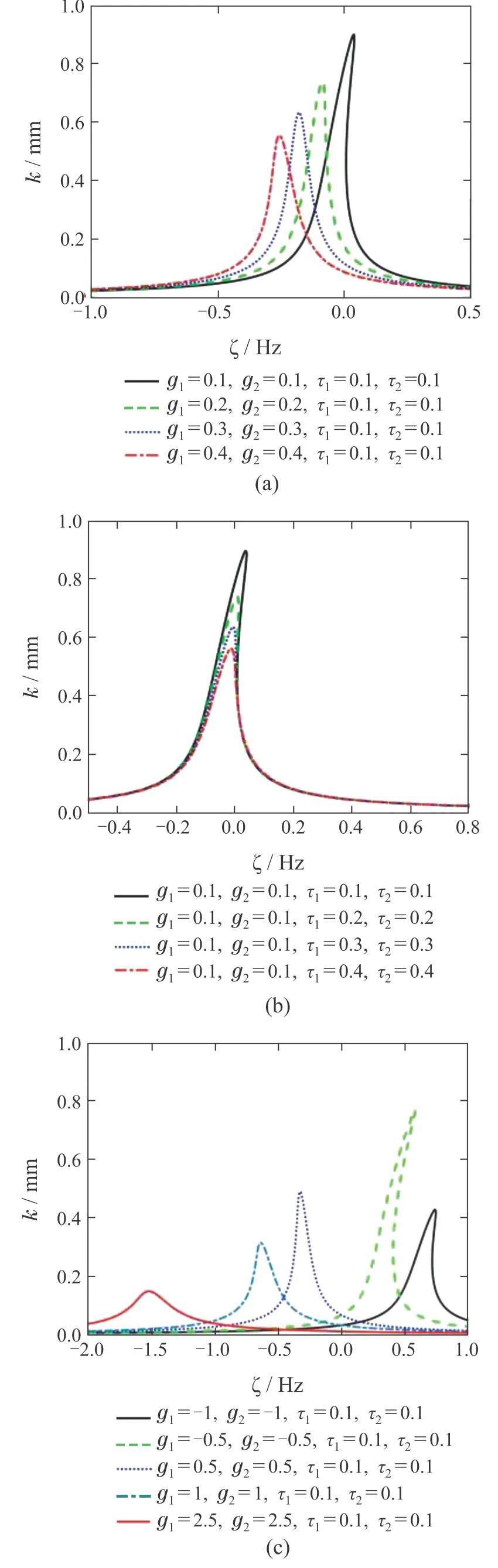
图13 不同控制参数对主共振时滞控制曲线的影响Fig.13 The time delay control curve of principal resonance with different parameters

6 结论

1)本文考虑了波纹辊轧机波纹界面间的非线性阻尼和非线性刚度,建立了波纹辊轧机两自由度垂直非线性主共振数学模型.利用奇异值理论和相平面法讨论了波纹辊轧机辊系自治下的稳定性,运用多尺度法求解了波纹辊轧机辊系在波纹界面激励下主共振的解析近似解和幅频特性方程.

2)通过数值仿真分析了非线性刚度系数、非线性阻尼系数、系统阻尼系数、轧制力的幅值等参数对波纹辊轧机辊系主共振的影响,验证了分析结果的正确性.通过设计时滞控制器来对波纹辊轧机辊系的主共振进行控制,通过适当调节时滞参数可以减小系统的响应幅值,避免分岔现象的发生.通过数值仿真验证了该控制器设计的正确性和可行性,为抑制波纹辊轧机的辊系振动和设计改造提供了一定的理论指导.

3)在波纹辊的设计过程中,可以通过减小波峰与波谷之间的距离、减少波纹的数量来对辊形曲线进行优化设计从而减小参激振动对轧制过程的影响.后续波纹辊轧机辊系主共振时滞反馈控制的研究将会通过最优算法来获得最佳线性和非线性反馈控制参数,并且结合智能抑振来对波纹辊的振动特性进行更深层次的研究.