比例阀控电液系统抗扰换向滞后补偿反步控制

刘胜斐,孙青林,陈增强,丁祉峰

(南开大学人工智能学院,天津 300350)

1 引言

电液系统因响应快、出力大、功率重量比大[1–7]在重型机械、机床制造、机器人等领域有广泛应用.常见的电液系统由电机驱动油泵将液压油吸入油管,采用伺服阀控制液压油的流量与压力,液压油流入油缸推动活塞带动负载移动,为了实现闭环控制,需要使用位移传感器和压力传感器分别检测位置信号和压力信号.

与伺服阀相比,比例阀制造成本低,对油液的清洁度要求低,抗污染能力强,为了降低电液系统成本,同时考虑到比例阀的控制精度与响应特性都能满足大多数工业控制系统实际需要[8],所以本文使用比例阀控制液压油的流量和方向.但是比例阀由于阀口重叠量而导致存在不灵敏区[9],进而引起换向滞后,负载移动过程中会受到外部干扰,液压油弹性模量随渗入油液的空气而变化,比例阀节流孔流量系数随雷诺数和阀口开度变化,以及液压系统中存在的未建模动态,这些因素使得采用比例阀实现电液系统精确位置控制的难度加大.

液压系统含有多种非线性特性[10],如流量压力非线性和负载与导轨间的摩擦非线性等,这些非线性特性加大了控制器设计难度.文献[11]使用反馈线性化方法实现了对油源压力波动的非线性电液系统精确位置控制.文献[12]设计自适应积分鲁棒控制器对双杆液压缸驱动的负载实现精确渐进跟踪.文献[13]研究了一种输出反馈非线性控制器,并将该控制器用于电液位置跟踪,使用奇异摄动理论分析了闭环系统的稳定性.文献[14]讨论了车辆电液制动系统在不同轮胎路面摩擦状况与初速变化下的鲁棒性,为电液制动系统设计了一种非线性模型预测控制器.文献[15]深入研究了电液主动悬架系统的非线性摩擦模型.

扰动会显著影响电液位置跟踪效果,文献[16]设计了一种二阶高通滤波器形式的扰动观测器用于估计扰动,采用变结构控制补偿扰动观测误差.为了使液压马达跟踪设定轨迹,文献[17]将未建模非线性摩擦和外部扰动看作总扰动设计了误差符号积分鲁棒控制器.文献[18]设计鲁棒柔顺控制器对含有关节角约束的电液机械臂实现角度控制.文献[19]提出一种鲁棒前馈观测器,用于飞行模拟器电液控制加载系统的感觉力控制.

为缩短比例阀换向滞后,使负载能迅速跟踪设定值并抑制干扰,本文使用线性扩张状态观测器对液压系统的外部扰动和内部扰动进行估计,将广义扰动看作扩张状态,进而为比例阀控电液系统设计抗扰反步控制器补偿参数不确定性和外部扰动,并分析了闭环系统的稳定性.

2 电液系统模型

图1为比例阀控电液系统原理图,该系统工作原理如下:电机驱动油泵从油箱中吸入液压油,油液通过过滤器和单向阀进入比例方向阀,控制器依据跟踪误差调整比例方向阀的控制电压,比例电磁铁得电后推动阀芯,比例阀的开度变化,液压油的流量和方向随之变化,油液通过比例方向阀进入液压缸,推动活塞移动,进而带动负载移动.比例阀控电液系统模型参数含义见表1.

根据牛顿第二定律,得到负载的动力学模型,如式(1):

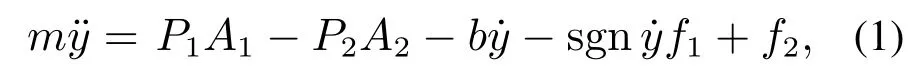
式中:m为负载质量,y为负载位移,P1为有杆腔压力,P2为无杆腔压力,A1为有杆腔活塞作用面积,A2为无杆腔活塞作用面积,b为活塞与液压缸之间的阻尼系数,sgn为符号函数,f1为负载与导轨之间的滑动摩擦力,f1µmg,µ为滑动摩擦系数,g为重力加速度,f2为未建模动态,包括未建模的摩擦非线性特性及其他难以建模部分.

液压缸动力学方程[20]如式(2):

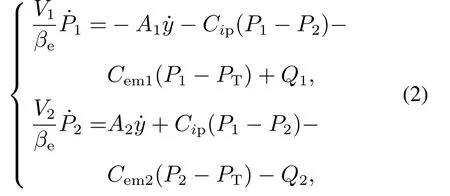
式中:V1,V2分别为有杆腔和无杆腔容积,βe为液压油弹性模量,Cip为液压缸内泄漏系数,Cem1,Cem2为液压缸外泄漏系数,PT为油箱压力,Q1,Q2分别为有杆腔流量和无杆腔流量.V1,V2如式(3):

式中V01,V02分别为有杆腔和无杆腔的初始容积.由于液压缸密封技术的进步,外泄漏系数可忽略,本文将Cem1,Cem2都取为0,于是得

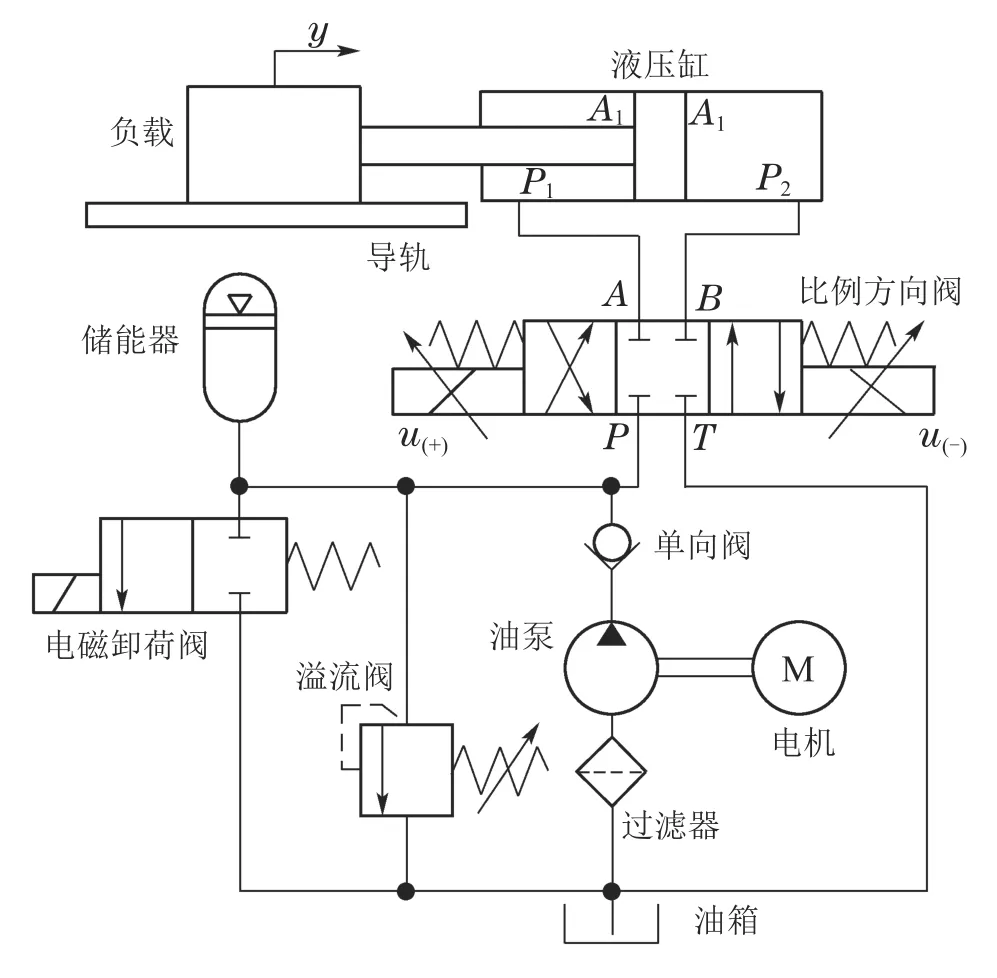
图1 比例阀控电液系统Fig.1 Proportional valve controlled electro-hydraulic system

表1 比例阀控电液系统模型参数含义Table 1 The meanings of parameters for the electrohydraulic system regulated by the proportional directional valve

本文使用三位四通比例方向阀调节液压油的流量和方向,液压油流量与比例方向阀阀芯净位移之间的关系[21]由式(5)–(6)描述为

式中:Cd,w,xnv分别为比例方向阀节流孔流量系数、节流孔面积梯度、阀芯净位移,ρ为液压油密度,PS为油泵压力.

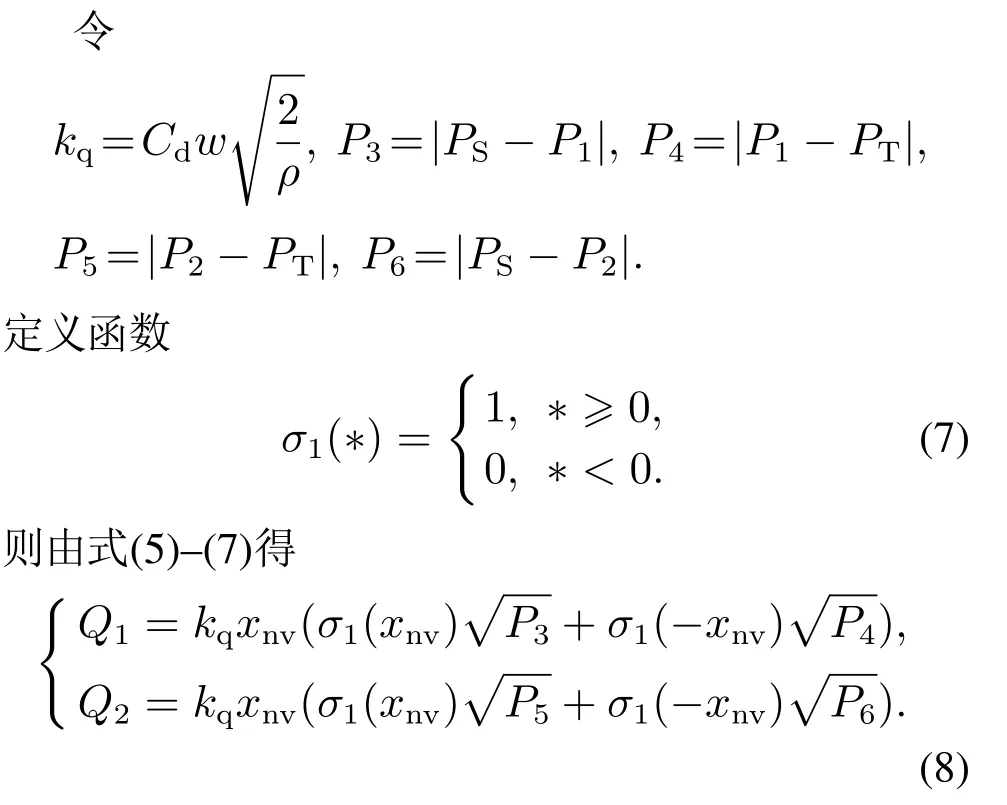
由式(8)知,调节比例方向阀的阀芯净位移可改变液压油的流量和方向.阀芯净位移和阀芯位移之间的关系[22]如式(9):

式中:xv为比例方向阀的阀芯位移,xvk0u,其中k0,u分别为比例方向阀的增益和控制电压,d1,d2为阀口的重叠量.阀芯净位移与控制电压之间的关系为

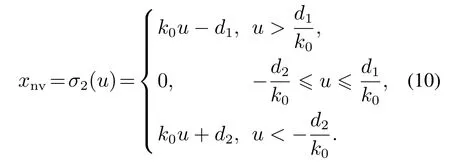
由以上分析可以得出单杆液压缸电液系统的输入输出关系为

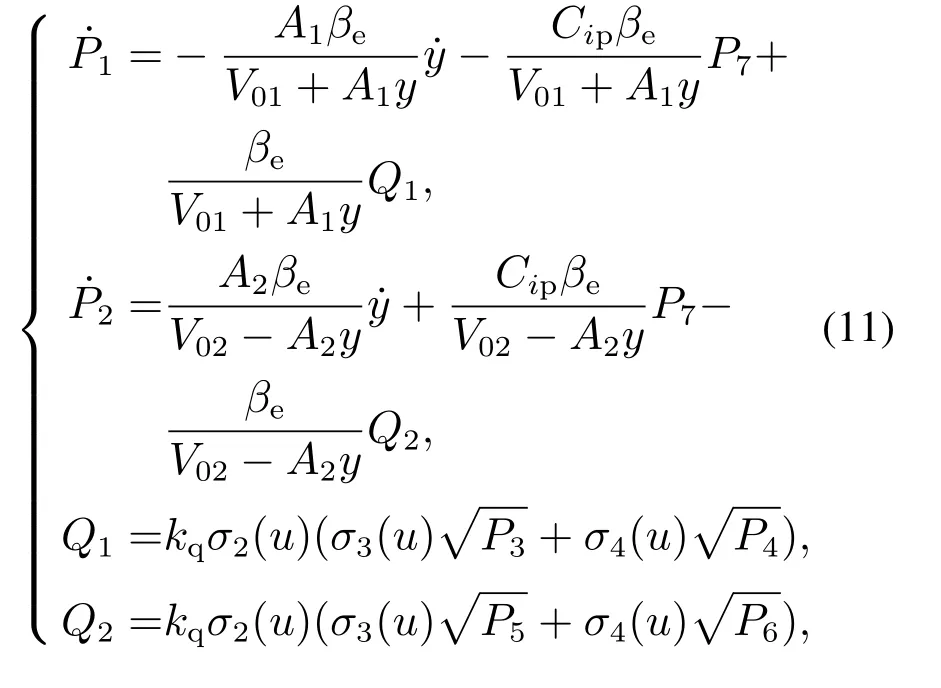
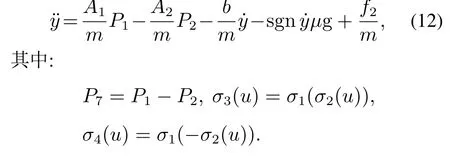
调节比例方向阀的控制电压可以改变阀芯位移,进而改变进入油缸的液压油流量和方向,而流量的大小决定了活塞移动的快慢,所以调节流量可以改变活塞移动的速度,进而改变负载移动的速度,负载位移随之改变.当控制电压为零时,阀芯回到中位,此时阀芯位移为零,油缸的进油口和回油口同时关闭,液压油流量为零,活塞停止移动,与活塞相连的负载停止移动.因此,调节比例方向阀的控制电压可以改变负载位移.

3 线性扩张状态观测器设计

扩张状态观测器[23–25](extended state observer,ESO)由我国著名系统与控制专家韩京清研究员提出,采用ESO可将难以处理的非线性、不确定因素看作总扰动,进而设计控制器对总扰动进行补偿[26–27],为了减小观测器的调试难度,文献[28]提出了观测器带宽,通过调整带宽可以确定线性扩张状态观测器(linear extended state observer,LESO)参数.由于比例阀控电液系统存在不灵敏区非线性、摩擦非线性与未建模动态,这些因素都会对负载位置造成影响,但很难测量,可将这些因素看作影响负载位置的扰动,进而将该扰动扩张成新的状态变量得到线性扩张状态观测器.本文使用线性扩张状态观测器根据测量到的比例方向阀控制电压和负载位置,估计电液系统受到的扰动,利用估计出的扰动信息设计控制器消除扰动对负载位置的影响.

由以上分析知:为了改变负载位移,需要调节比例方向阀的控制电压,而式(11)却不显含控制电压,因此需从式(11)中寻找与控制电压有关的量.由于比例方向阀调节的是液压油的流量与方向,而流量改变会引起活塞移动速度变化,进而引起负载速度变化,所以式(11)中与速度有关的量都与流量有关,进而都与控制电压有关,因此得

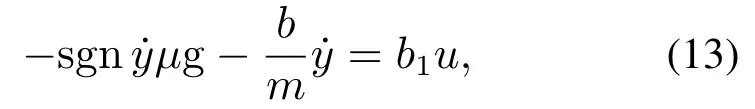
其中:b1是控制电压的放大系数,b10,可以根据控制效果确定b1.将式(13)代入式(11)得

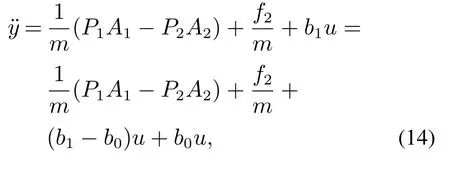
其中: b0是补偿因子,b0≈b1,uu1+w1,u1为控制器的输出,w1为外部扰动.因此,得

其中f为广义扰动,包含内部扰动、外部扰动和未建模动态.将广义扰动看作扩张状态,选取状态变量x1y,x2则式(17)可化为

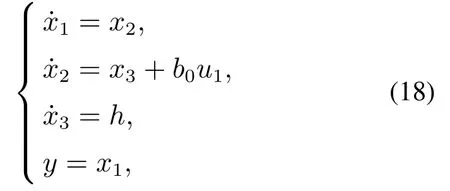
式中:x3是扩张状态,h式(18)可写成矩阵形式

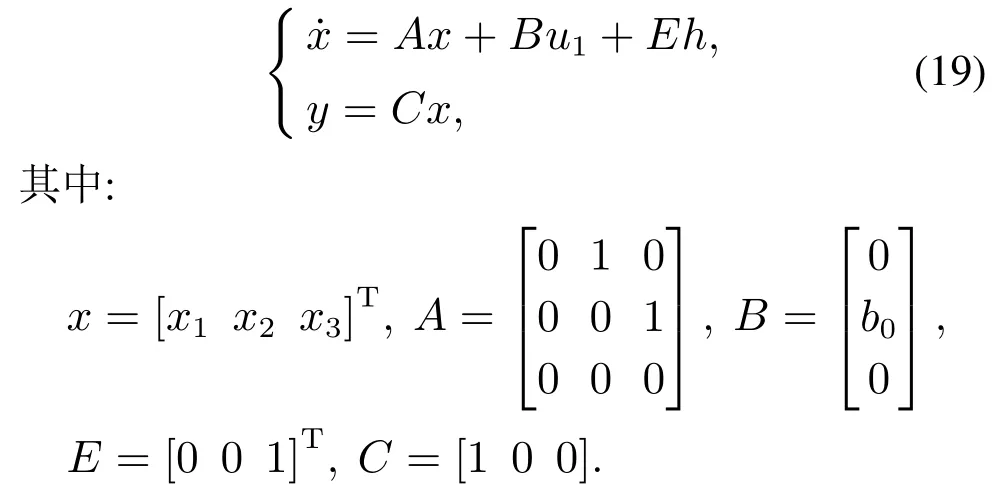
为系统(19)设计线性扩张状态观测器

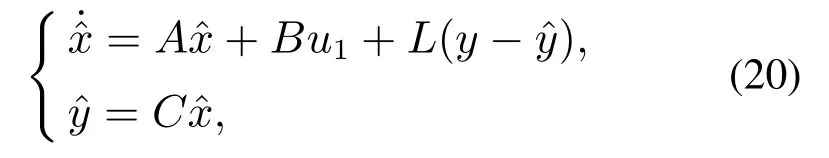
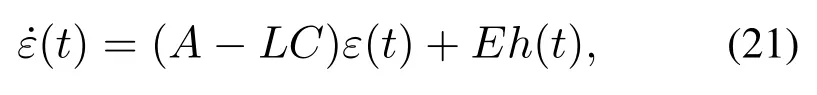
其中h(t)是广义扰动的导数,由式(16)知,h(t)有界,

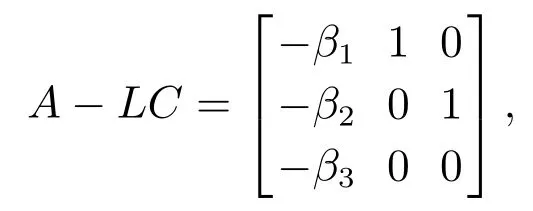
A −LC的特征多项式为

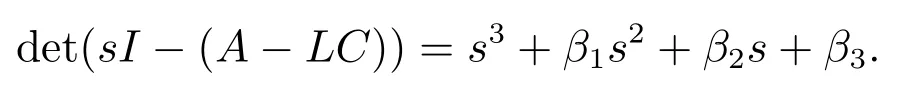
因为h(t)有界,为了线性扩张状态观测器有界输入有界输出稳定,需将A −LC的特征根都配置在左半复平面.用ωo(ωo>0)表示观测器带宽,可将A −LC的特征根都配置在−2ωo,

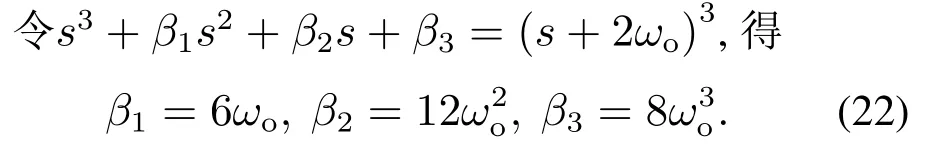
4 控制器设计

由于本文采用比例方向阀控制液压油的流量和方向,然而比例方向阀具有不灵敏区非线性特性,从而导致换向滞后,同时电液系统存在外部干扰,液压油弹性模量随渗入的空气而变化,这些因素增加了设计电液位置控制器的难度.可以使用反步法(backstepping)[29–30]为含有不确定性的非线性系统设计鲁棒控制器,本文使用线性扩张状态观测器实时估计电液系统中存在的内外扰动,进而设计抗扰反步控制器补偿比例阀的换向滞后与其他扰动,将所得控制电压作用于比例方向阀,缩短换向滞后并提高电液系统的抗扰能力.

本文使用正弦信号和阶跃信号作为电液系统的设定值.跟踪正弦信号时,r(t)A3sin(ωt),其中r(t)为设定值,A3,ω分别为正弦信号的幅值、频率;跟踪阶跃信号时,为了减少动态过程的超调,使用双曲正切函数对阶跃设定值进行柔化,如式(23)所示:

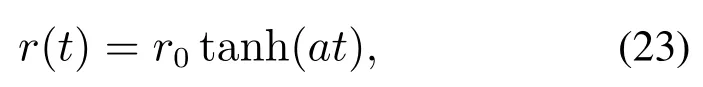
其中:r0为阶跃设定值,tanh为双曲正切函数,a(a>0)为柔化因子,调节a可改变收敛速度,r(t)为柔化后的设定值.由式(23)得式(24)–(26)

从式(24)–(25)看出,随着时间的推移,r(t)单调递增收敛至r0,因此只要负载能够跟踪r(t),负载最终必然到达设定位置r0.

为计算控制量u1,首先定义李雅普诺夫函数

其中跟踪误差ξ1r −y.由式(27)得

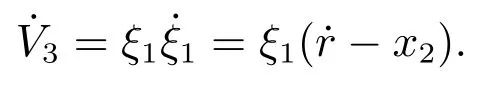
定义虚拟控制量ξ2为

其中:k为控制器增益,β为广义扰动的观测误差上界,

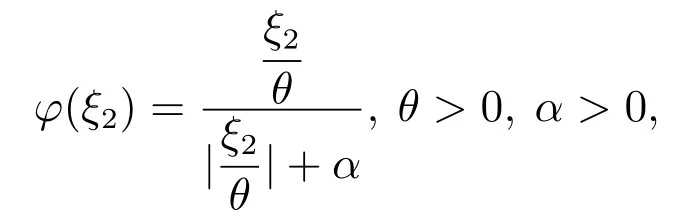
5 稳定性分析

为保证比例阀控电液系统长期稳定运行,需要进行稳定性分析.由于本文的控制器设计与扰动的估计值有关,所以首先对线性扩张状态观测器的观测误差作分析,然后分析电液系统的跟踪误差.通过稳定性分析,可以找到与观测误差和跟踪误差有关的控制器参数[31],进而选择合适的参数取值范围,确保电液系统能稳定运行,同时提高系统的跟踪精度.

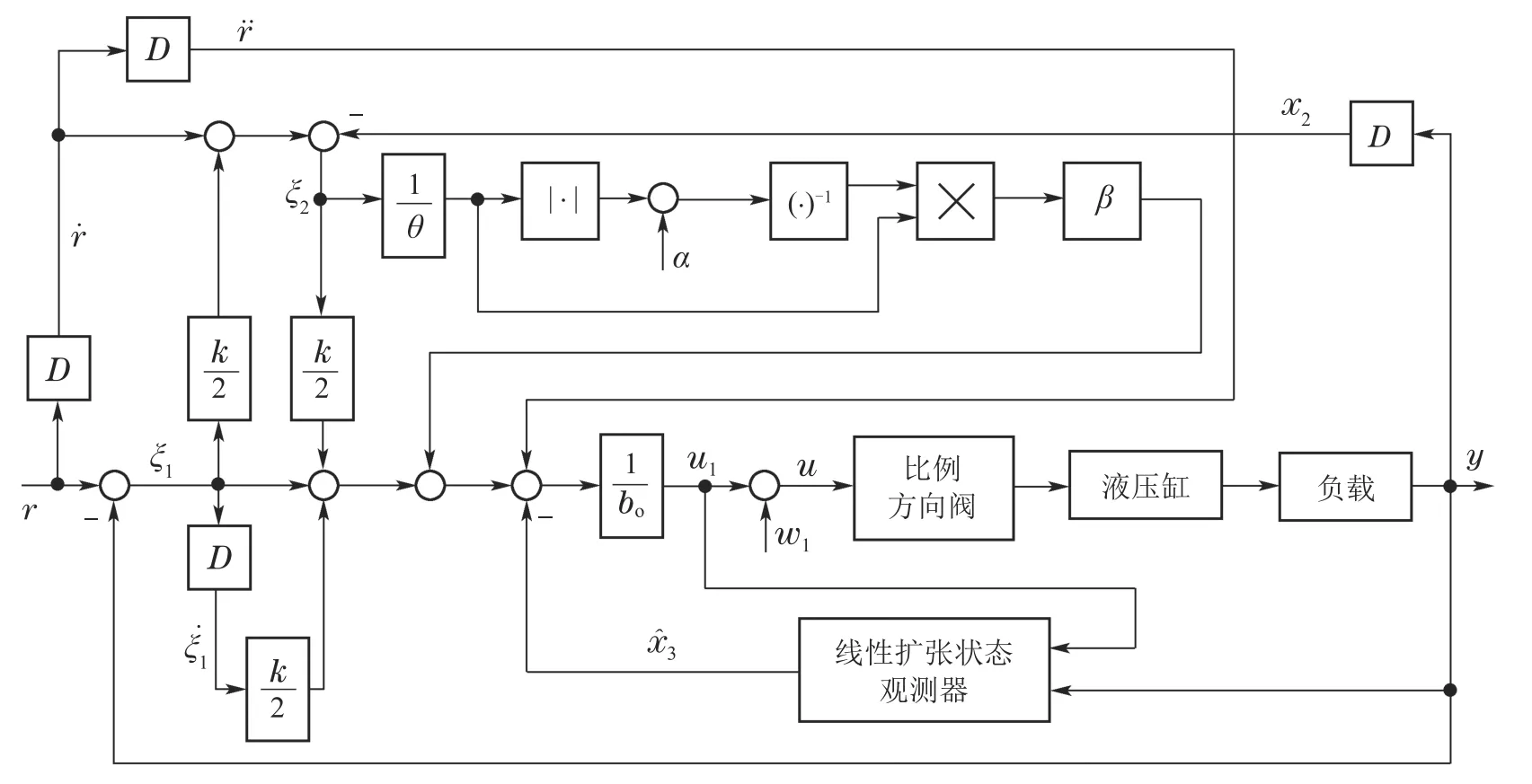
图2 比例阀控电液系统结构图Fig.2 Block diagram of the electro-hydraulic system

5.1 观测误差分析

参考文献[32]的分析方法,下面讨论当观测器增益取值为式(22)时的观测误差.由式(20)得

将式(22)代入式(36),得

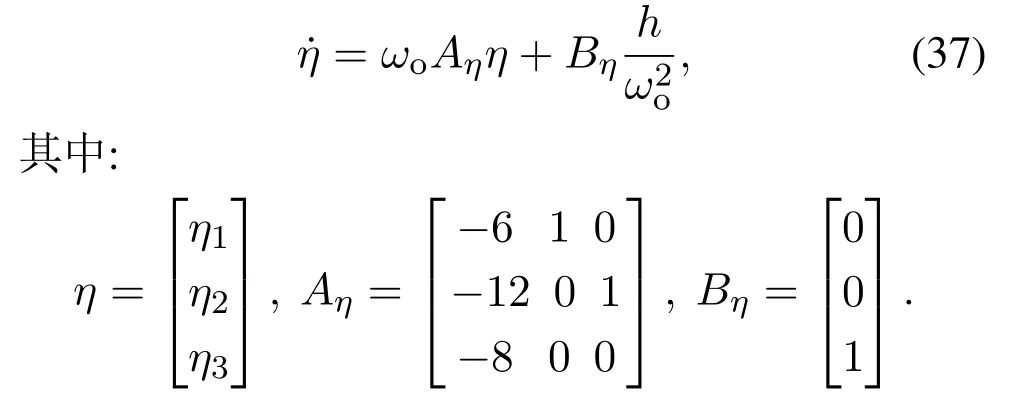
定理1假设h有界,则存在一个正数Mi(i1,2,3),及有限时间T1>0,当tT1时,|εi(t)|Mi;Mi与ωo有关,且其中:

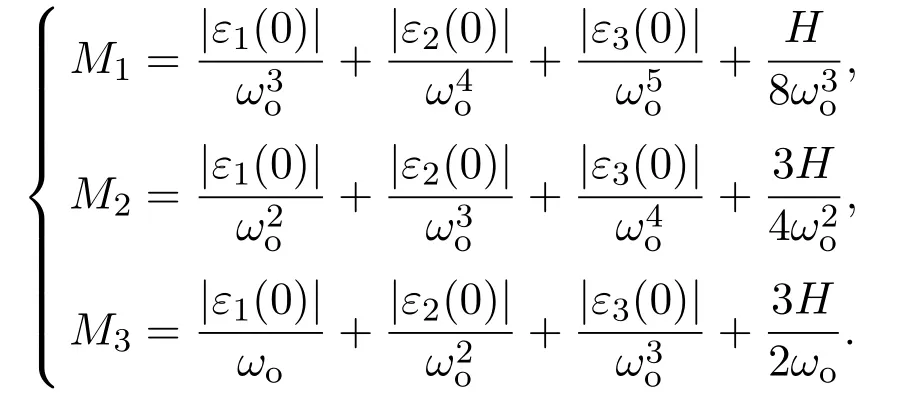
证微分方程组(37)的解为

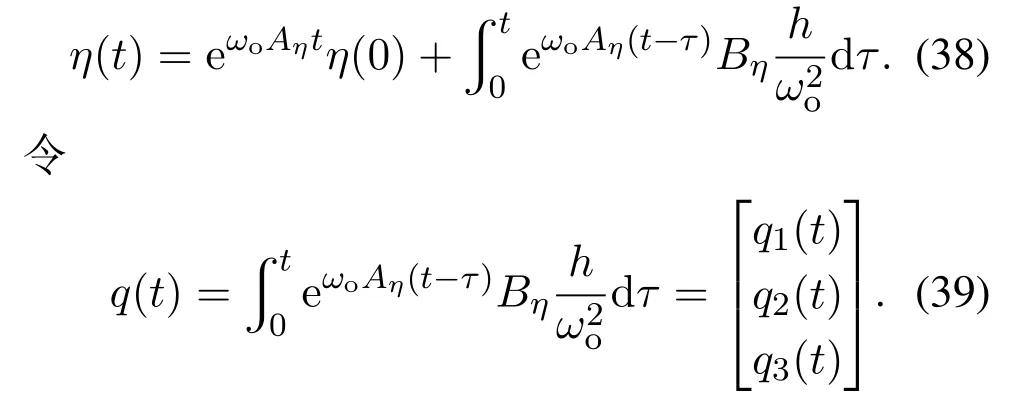
由于Aη的特征根是−2(三重),所以ωoAη的特征根是−2ωo(三重),得

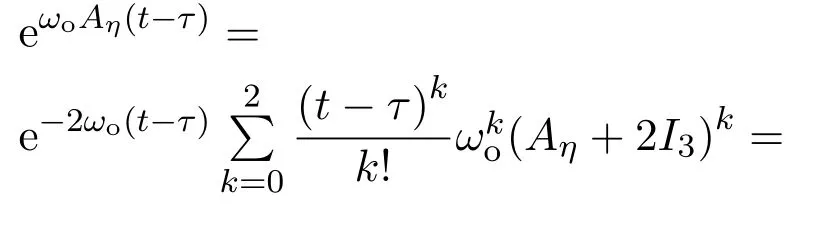
其中: I3为3阶单位矩阵,

将式(40)代入式(39),得

同理可得

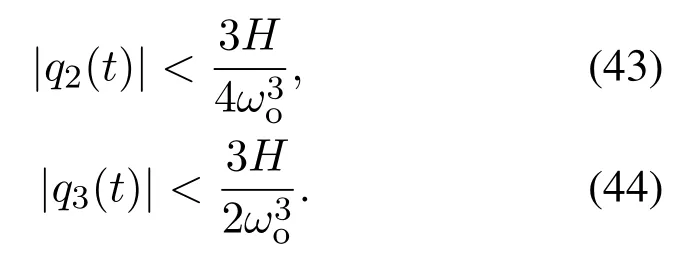
因为ωoAη的特征根是−2ωo(三重),所以

将式(39)(45)代入式(38),得

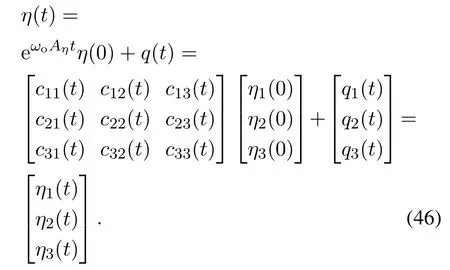
首先分析状态变量x1(t)的观测误差上界.当tT1时,由式(42)知|q1(t)|所以

从以上分析知,当扰动导数有界时,线性扩张状态观测器的观测误差也是有界的,增大观测器带宽可减小观测误差,当观测器带宽增大时,观测误差趋近于零.证毕.

5.2 跟踪误差分析

为了分析比例阀控电液系统的跟踪误差,需要以下引理.

引理1对于任意z ∈R,θ >0,α>0,有

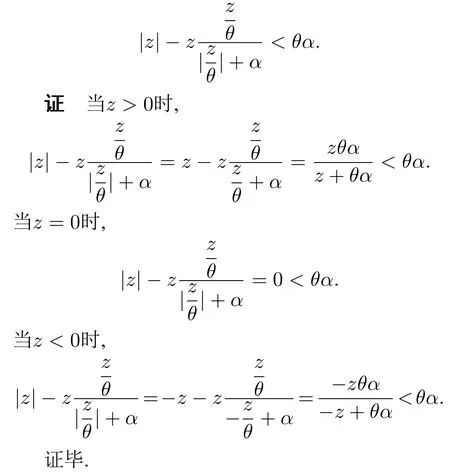
定理2假设h有界,则控制量u1使电液系统的跟踪误差ξ1与跟踪误差导数最终一致有界.

证将式(32)代入式(31),得

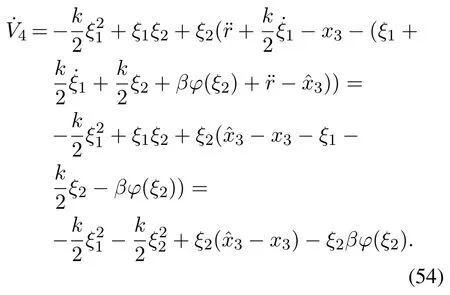
因为h有界,由定理1知,存在M3>0,T1>0.n 当β,进而有ξ2β|ξ2|,所以

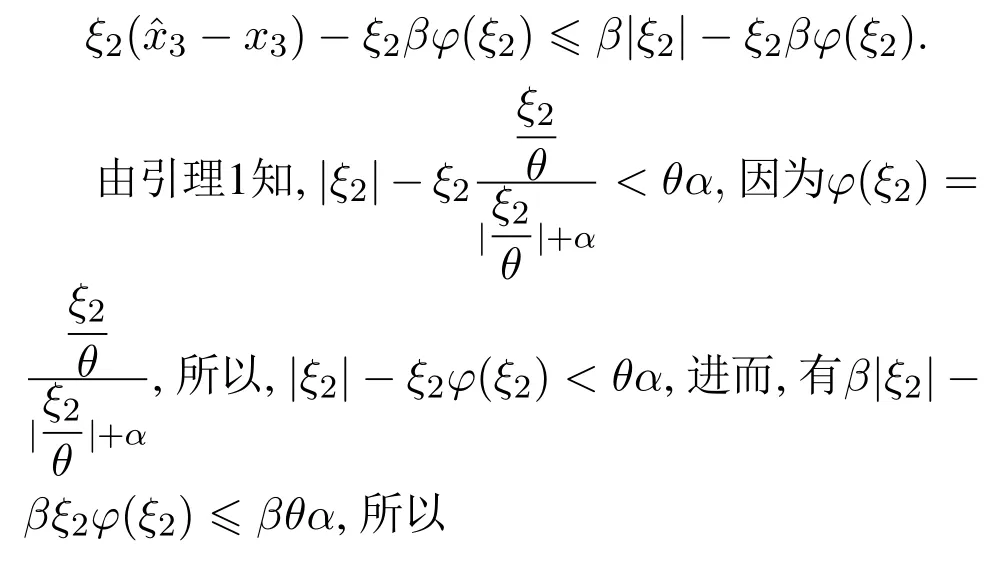
由式(56)知,为了减小跟踪误差,需要增大k,由式(59)知,当k >2时,随着k增大,跟踪误差导数的上界增大,从而引起振荡,为减小振荡,需要减小θ,α.由上述分析知,当扰动导数有界时,控制量u1使电液系统的跟踪误差与跟踪误差导数最终一致有界,调整控制器参数k,θ,α可使跟踪误差收敛到原点附近.证毕.

6 仿真

为了验证电液位置的控制效果,本文进行了MATLAB仿真,仿真采用的电液系统参数如表2.跟踪阶跃信号时,为减少负载位置的超调,本文使用双曲正切函数对设定值进行柔化.

表2 电液系统参数表Table 2 Parameters for the electro-hydraulic system

如图3所示,设定值为20 mm,若未对设定值柔化,在0.25 s时负载到达22.02 mm处,超调量为10.1%,而采用双区正切对设定值柔化后可显著减小负载位置超调量.

图3 对设定值柔化后的跟踪效果图Fig.3 Tracking the smoothed set value

调节柔化因子可以改变负载位置收敛到设定值的速度,如图4所示.

图4 调节柔化因子改变收敛速度Fig.4 Changing the convergence rate by adjusting the smooth factor

在图4中,a为柔化因子,从图中可以看出在0.8 s时,若a0.8,则负载移动到11.8 mm处,若a1.5,则负载移动到16.9 mm处,若a3,则负载移动到19.3 mm处.因此,增大柔化因子可加快收敛速度.

若观测器带宽ωo50,补偿因子b012,跟踪柔化后的阶跃信号时,位置x1,广义扰动x3与相应的观测值如图5–6所示.

由图5知,在0.306 s时位置信号x1与估值分别为13.76 mm,13.83 mm;在0.317 s时位置信号x1与估值分别为14.16 mm,14.22 mm;在0.752 s时位置信号x1与估值分别为19.21 mm,19.22 mm.

由图6知,在0.921 s时广义扰动x3与估值分别为47.75 m/s2,55.90 m/s2;在0.967 s时,x3与估值分别为93.86 m/s2,97.36 m/s2;在1.912 s时,x3与估值分别为60.50 m/s2,60.93 m/s2.

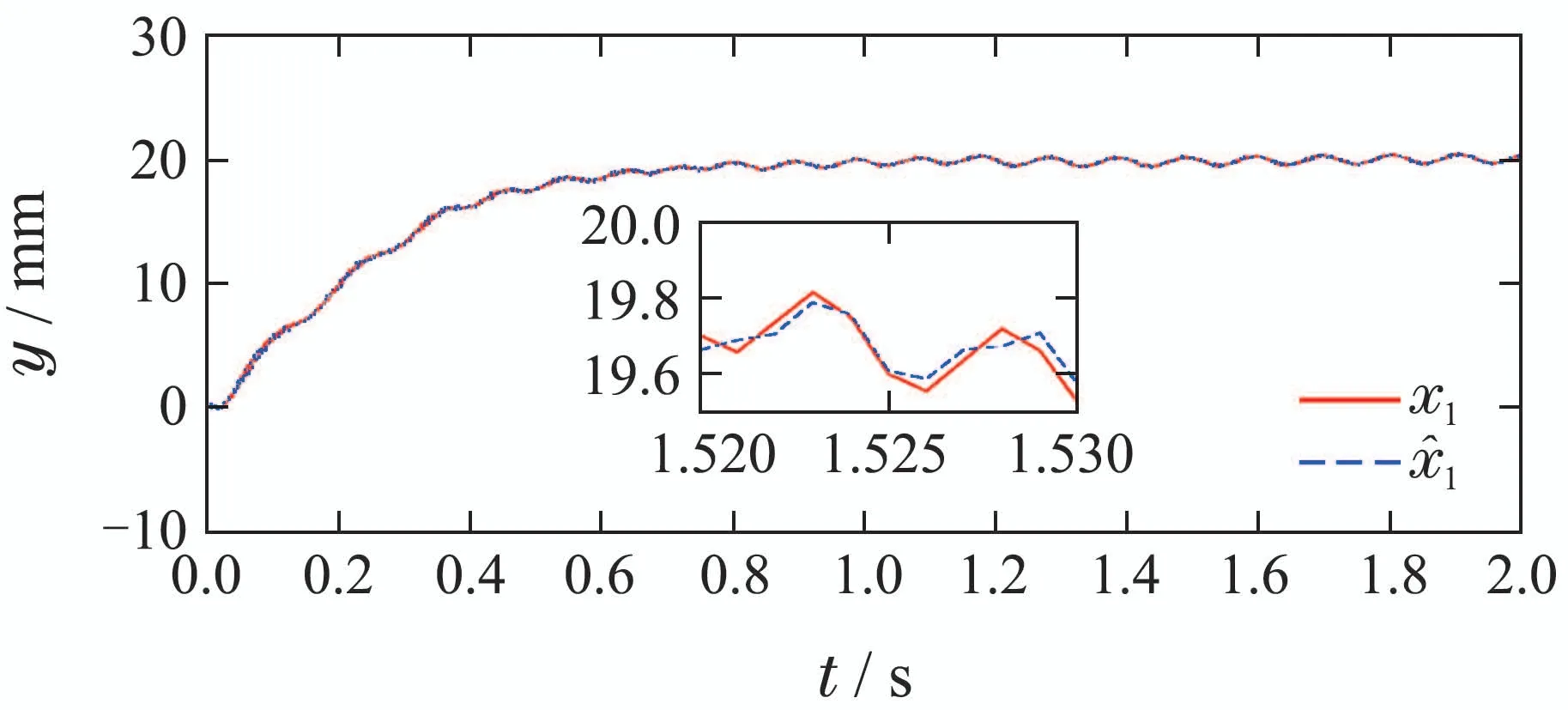
图5 跟踪阶跃信号时的x1与估值Fig.5 x1 and its estimate when tracking step signal

图6 跟踪阶跃信号时的x3与估值Fig.6 x3 and when tracking step signal

由图5–6知,跟踪阶跃信号时,ESO能准确估计位置和广义扰动.

通过调整控制器参数k,θ,α可以改变跟踪误差,如图7所示.

图7 调整控制器参数改变跟踪误差Fig.7 Changing the tracking error by adjusting the controller parameters

液压油弹性模量随渗入油液的空气而变化.在图8中,液压油弹性模量在2.43×108Pa 和2.97×108Pa之间变化.当弹性模量如图8变化时,采用比例积分微分(proportional integral derivative,PID)控制器和本文设计控制器的跟踪误差如图9所示.

由图9知,在0.36 s时,PID控制器和本文设计控制器的跟踪误差分别为20 mm和5.38 mm,在3.1 s时,PID 控制器和本文设计控制器的跟踪误差分别为5.50 mm和0.05 mm.

图8 液压油弹性模量发生变化Fig.8 Variation in the oil effective bulk modulus

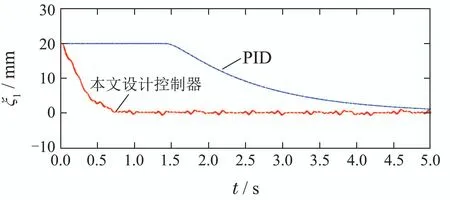
图9 弹性模量发生变化时的跟踪误差Fig.9 Tracking error with the variation in the effective bulk modulus

因此与PID控制器相比,本文设计的控制器在弹性模量发生变化时的跟踪误差更小,从而有更强的鲁棒性.由式(10)知,比例阀的阀口有重叠量,使用PID控制器难以快速跟踪设定值.

为验证控制器的抗扰能力,本文对控制器的输出电压加入干扰信号,进而用含有扰动信号的控制电压驱动比例阀.本文设计控制器与PID控制器的抗外扰能力比较如图10所示.PID控制器参数: kP160,kI120,kD0.01.本文设计控制器参数:ωo50, k30, β60, θ0.001, α0.002,b012.

由图10知,从0 s至2 s,PID控制器的跟踪误差由20 mm减小为13.3 mm,而同一时段内,本文设计控制器的跟踪误差由20 mm减小为0.07 mm,说明本文设计控制器比PID控制器的跟踪速度快;在7.5 s时,由于对控制电压加入3.2 V扰动,负载偏离设定值,PID控制器作用下负载最大偏离16.7 mm,而本文设计控制器作用下负载最大偏离6.2 mm;在8 s时,PID控制器的跟踪误差为−16.6 mm,而本文设计控制器的跟踪误差为−0.1 mm,表明与PID控制器相比,本文设计控制器的抗扰能力更强,跟踪精度更高.

图10 本文设计控制器与PID控制器的抗外扰能力比较Fig.10 Comparison of the external disturbance rejection ability between the proposed controller and PID controller

比例方向阀由于阀口重叠量而导致换向滞后,以跟踪正弦信号r(t)20 sinmm为例,PID控制器与本文设计控制器的跟踪效果分别如图11–12所示.PID控制器参数kP180,kI150,kD0.02;本文设计控制器参数k30,θ0.001,α0.001,β60,ωo60,b012.

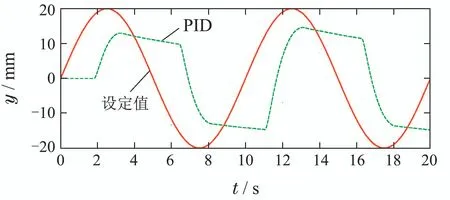
图11 PID控制器跟踪正弦信号Fig.11 Tracking the sinusoid signal with PID controller

图12 本文设计控制器跟踪正弦信号Fig.12 Tracking the sinusoid signal with the proposed controller

由图11–12可知,在2.5 s时发生换向,设定值为20 mm,PID控制器和本文所设计的控制器作用下的负载位置分别为9.3 mm和19.7 mm;在7.5 s时再次发生换向,设定值为−20 mm,PID控制器和本文所设计的控制器作用下的负载位置分别为−9.6 mm和−19.9 mm.

因此,在发生换向时,PID控制器的跟踪误差较大,存在较大的换向滞后,而本文设计的控制器能较好补偿换向滞后,迅速跟踪设定值.跟踪正弦信号时,位置x1,广义扰动x3与相应的观测值如图13–14所示.由图13可知,在0.159 s时,位置x1与估值分别为2.02 mm,2.31 mm;在0.253 s时x1与估值分别为3.38 mm,3.13 mm;在15.26 s时x1与估值分别为−3.33 mm,−3.29 mm.由图14 可以看出,在6.176 s时,广义扰动x3与估值分别为61.80 m/s2,58.17 m/s2;在8.395 s时,x3与估值分别为39.21 m/s2,38.20 m/s2;在16.326 s时,x3与估值分别为13.16 m/s2,12.65m/s2.

图13 跟踪正弦信号时的x1与估计值Fig.13 The position signal x1 and its estimate when tracking sinusoid signal

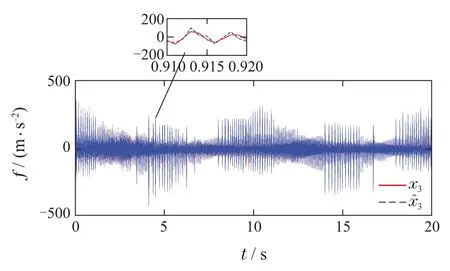
图14 跟踪正弦信号时的x3与估计值Fig.14 x3 and its estimate when tracking sinusoid signal

由图13–14知,在跟踪正弦信号时,ESO能准确估计负载位置和广义扰动.

7 实验

本文在实验台上验证了控制器的性能,实验台如图15所示.本实验台采用博世力士乐4WREE6E 08–2X/G24K31/A1V比例方向阀,该比例阀含有内置驱动放大电路,电源电压为直流24 V,最大电流2 A,最大流量80 L/min,最大压力315 bar;负载质量为3.65 kg,油泵压力为6 MPa,使用功率为0.75 kW的交流电机拖动油泵,电机转速为1400 r/min;油缸外径,行程分别为40 mm,200 mm;活塞与活塞杆的直径分别为32 mm,16 mm;使用型号为米朗KTC–300的直线位移传感器测量负载位移;采用型号为易福门PT5402压力传感器测量油缸压力;使用阿尔泰科技USB3120数据采集卡实现计算机与电液系统间的测量信号与控制信号传输,该采集卡采样率为2.5×105sps,转换精度16位.使用计算机计算比例方向阀的控制信号,CPU主频2.5 GHz,内存8 GB,采用C++语言编写控制程序,采样周期10 ms.

图15 比例阀控电液系统实验台Fig.15 Experimental bench for the electro-hydraulic system

在跟踪阶跃信号时,为了减小超调量,本文使用双曲正切函数安排过渡过程,对设定值进行柔化,跟踪效果如图18所示.控制器参数为ωo33,k32,β60,b09,θ10−5,α10−7.

由图16知,设定值为30 mm,在1.1 s时,若未对设定值柔化,则负载位置为36.7 mm,超调量为22.3%;若采用柔化因子为1.2的双曲正切对设定值柔化,则负载位置为27.0 mm.因此,使用双曲正切柔化阶跃设定值可显著减小超调量.

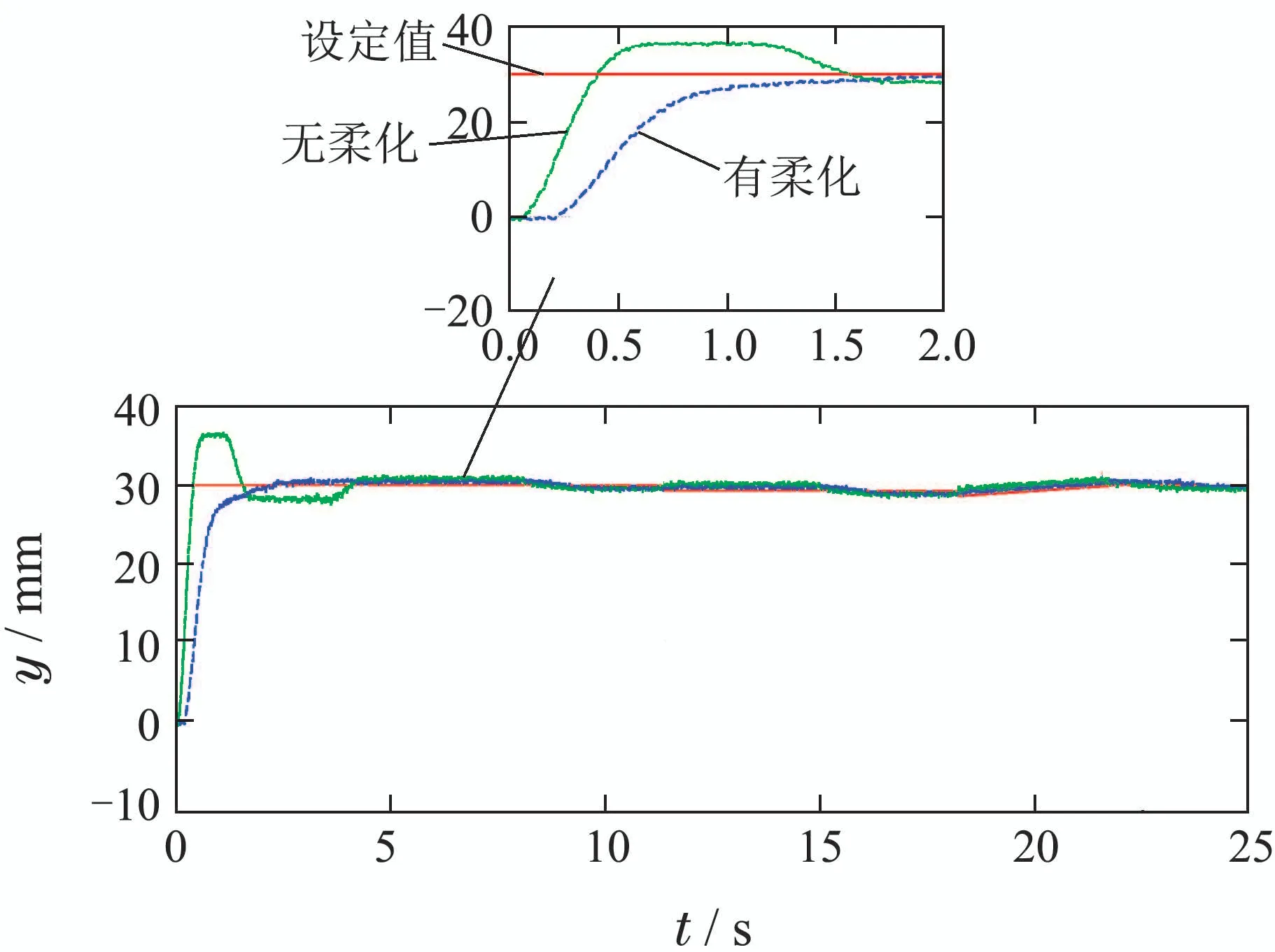
图16 使用双曲正切安排过渡过程Fig.16 Arranging transition process with hyperbolic tangent

本文设计控制器与PID控制器抗外扰能力比较如图17所示.本文设计控制器参数为ωo35,b010,β60,k80,θ10−6,α10−8;PID控制器参数为kP200,kI160,kD0.01.

图17 控制器抗外扰能力比较Fig.17 Comparison of external disturbance rejection ability of controllers

由图17知,设定值为60 mm,为比较控制器的抗扰能力,在20 s时,对比例阀的控制信号加入−2.1 V扰动,在该扰动作用下,负载偏离设定值,本文设计控制器和PID控制器作用下负载位置最大偏差分别为4.2 mm和8.0 mm.若误差带取±2%,则扰动发生后,本文设计控制器和PID控制器的调节时间分别为0.3 s和4.1 s.因此,本文设计控制器能使负载很快恢复到设定值,具有很强的抗扰能力.

本文设计控制器与PID控制器跟踪正弦信号时的负载位置如图18–19所示.正弦信号在1个周期内发生2次换向,设定值为60 sinmm.

本文设计控制器参数为ωo30,k60,β60,θ0.001,α0.001;PID控制器参数为kP120,kI110,kD0.001.

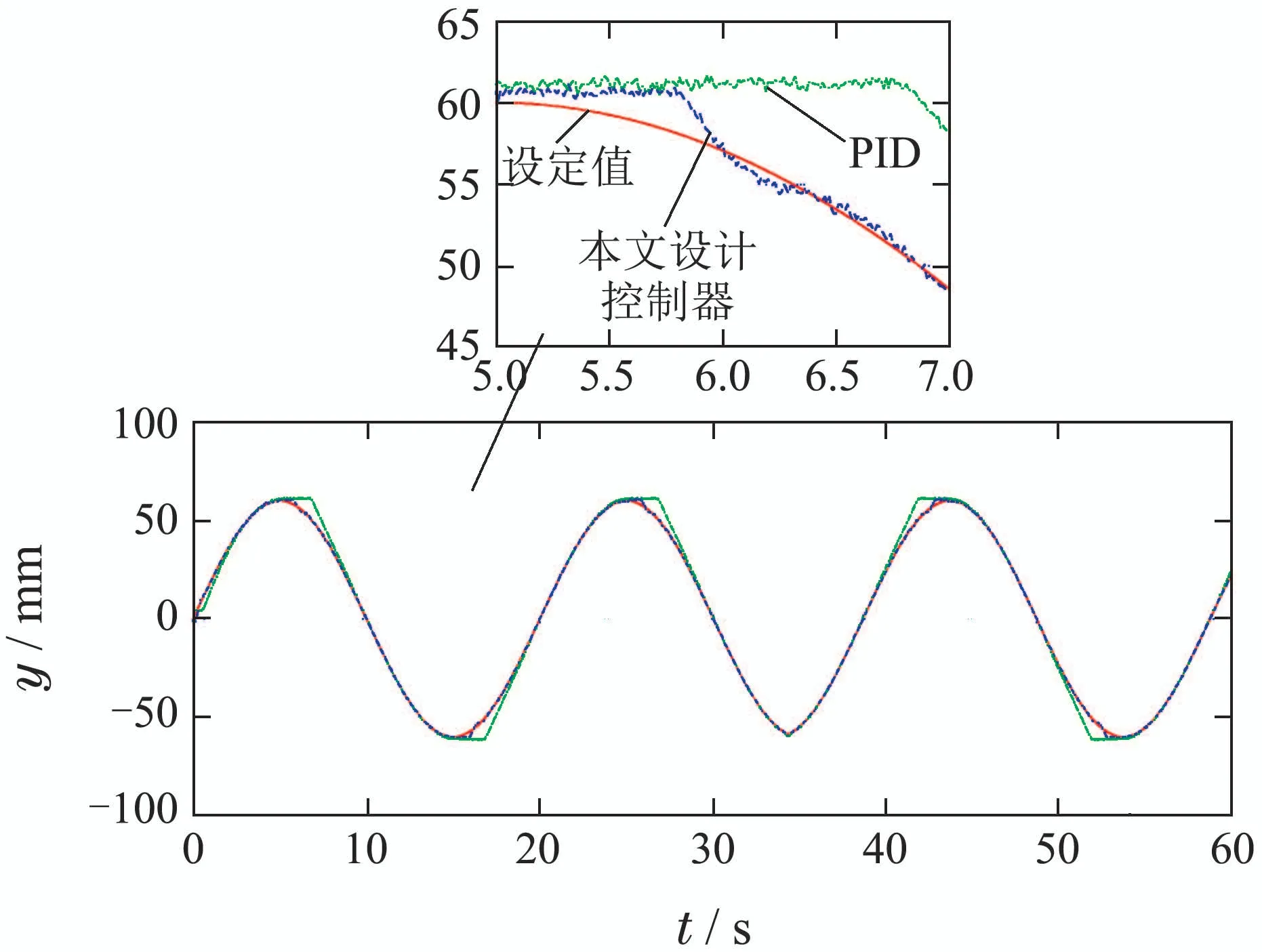
图18 第1次换向发生时跟踪效果比较Fig.18 Comparison of tracking result with the first direction switch

由图18知,在5 s时,正弦信号发生第1次换向,在6 s时,本文设计控制器和PID控制器作用下的负载跟踪误差分别为−0.5 mm和−4.1 mm.

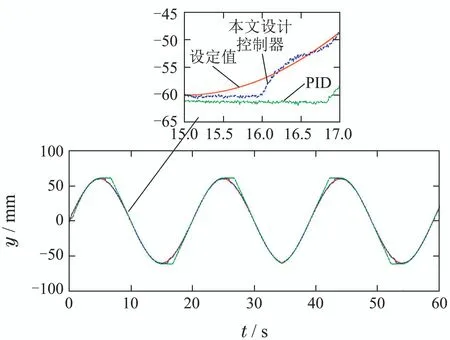
图19 第2次换向发生时跟踪效果比较Fig.19 Comparison of tracking result with the second direction switch

由图19知,在15 s时发生第2次换向,在16.2 s时,本文设计控制器和PID控制器作用下的负载跟踪误差分别为0.007 mm和5.5 mm.因此,本文设计控制器可以缩短换向滞后,使负载迅速跟踪设定值.

为了减小跟踪误差,需要调整控制器参数,设定值取为20 mm,负载初始位置为0 mm,在不同控制器参数下的跟踪误差如图20–22所示.通过比较图20–22在1.5 s后的跟踪误差,可以发现调整控制器参数会引起跟踪误差发生显著变化.

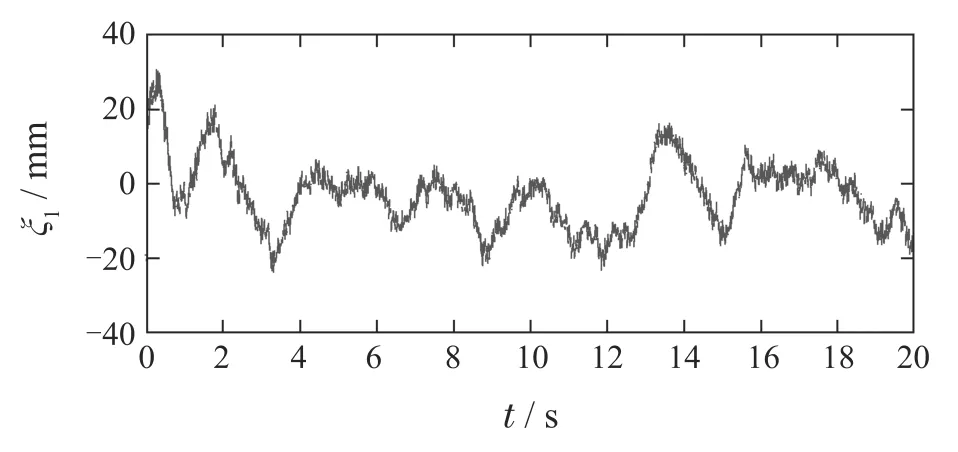
图20 k=5,θ=0.008,α=0.007时的跟踪误差Fig.20 The tracking error when k=5, θ=0.008,and α=0.007

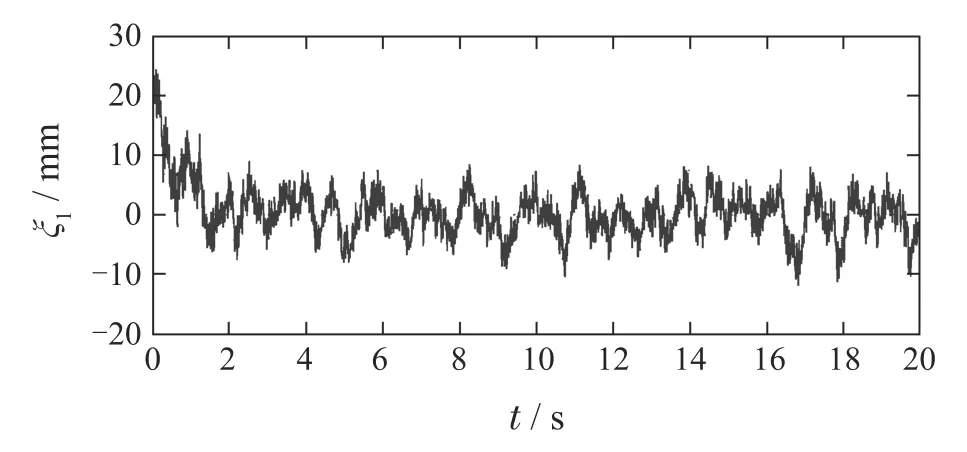
图21 k=30,θ=0.008,α=0.007时的跟踪误差Fig.21 The tracking error when k=30, θ=0.008,and α=0.007

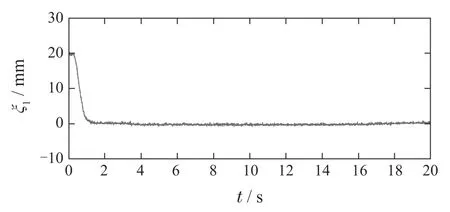
图22 k=30,θ=10−6,α=10−5时的跟踪误差Fig.22 The tracking error when k=30, θ=10−6,and α=10−5

8 结论

本文采用线性扩张状态观测器实时估计电液系统存在的难以测量的比例阀阀口重叠量和液压油弹性模量,外部扰动与未建模动态,设计抗扰反步控制器对总扰动进行补偿,使用双曲正切安排过渡过程,从而显著减小超调,研究了电液位置控制系统的稳定性,证明在扰动导数有界的前提下,观测误差和跟踪误差都有界.仿真和实验表明:控制器增益k增大到一定值时,非线项参数θ,α越小,跟踪误差越小,进而收敛到原点附近,与PID控制器相比,本文设计控制器可快速跟踪设定轨迹,在外扰发生时,能迅速恢复到设定值,缩短比例阀换向滞后,进而实现负载位置精确控制.