大跨距细长型复合丝杠结构动态特性分析
2020-08-14杨灵均张志强王黎钦
杨灵均 张志强 殷 琪 王黎钦
0 引言
丝杠传输结构常用于进给结构或伺服定位结构的进给和定位中,是一种运动形式转换的结构,具备较好的承载能力、抗冲击性、环境适应能力。对于该大跨距细长型复合丝杠结构,由于丝杠结构在运行过程中极易出现振动等现象,从而使得细长型丝杠产生大变形与振动,从而对传输位置的准确性、系统的稳定性,甚至其使用寿命产生影响。
为研究丝杠结构系统的动态特性,建立完整的丝杠、转子的动力学模型至关重要。Velinsky 等[1]研究了典型的行星滚柱丝杠结构的弹性变形,表明了弹性变形对丝杠结构的动态传输效率有着重要的影响。党金良等[2]等建立了典型的行星滚柱丝杠结构的多体动力学模型。通过仿真分析发现,随着外部载荷的变化对其接触载荷有着重要的影响。Schinstock 等[3]分析动态载荷对丝杠结构的影响,结果表明在允许静载荷范围内的动态载荷也可能导致结构的损坏。
除此之外,丝杠结构的振动状态对系统的动态特性有着重要的影响。其中运行摩擦力矩的稳定性是丝杠结构产生振动的主要原因,反之,系统的振动也会影响到结构的摩擦力矩大小及稳定性。Olofsson 等[4]研究发现丝杠螺母结构振动与自激振动有关,而自激振动受摩擦系数、滑动速度、润滑、固有频率等因素的影响。Dupont 等[5-6]利用单自由度模型很好地解释了丝杠结构振动现象,发现结构的稳定性与螺母及丝杠的质量、摩擦系数及螺旋角有关。通过建立数学模型和3D 模型对丝杠螺母结构振动和稳定性问题的研究也有较大的发展。[7-9]张武等[10]通过对其丝杠螺母运动副模型的建立,分析了运转中摩擦系数变化对其稳定性的影响。结果表明,摩擦系数的减小有利于结构的稳定性。周勇等[11]采用集中参数法建立考虑扭转振动与轴向振动的滚珠丝杠副进给结构动力学模型,进行动力学特性模拟,提出滚珠丝杠滚振的概念。Chen[12]和Wang[13]等针对丝杠结构的振动问题,提出了一种分析模型来研究预载荷对滚珠丝杠非线性动力学特性的影响。研究发现,适当的预紧力可以抑制振动,提高稳定性。
目前,针对丝杠结构在偏心状态下的支撑载荷及摩擦力矩研究较少。本文将通过对某丝杠结构多体动力学模型的建立,在大长径比、低转速及多点支撑的特点下,研究了其动力学特性,分析了轴承磨损造成转子偏心的情况对轴承作用力及啮合区摩擦力矩的影响。
1 模型建立
大跨距细长型复合丝杠结构主要由细长型丝杠、大跨距转子、滚轮、支撑轴承以及浮动支撑等组成。其中,三个支撑轴承等间距分布在转子上,轴承外圈固定,内圈与转子相连,并以低转速进行旋转。转子旋转的同时,通过丝杠与滚轮之间的螺纹啮合(局部放大区),从而实现丝杠沿竖直方向的上下移动。
为建立模型的方便性及计算的快速性,对丝杠及轴承进行了相应的简化,建立了基于ADAMS 的多体动力学模型。图1 为轴承模型的简化模型。
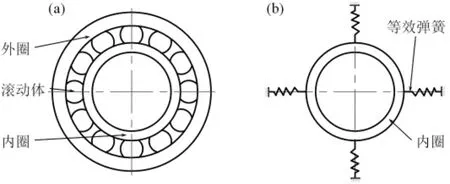
图1 轴承等效模型示意图
1.1 轴承简化
由于轴承是由多个组件构成的部件,因此在结构模型中很难建立轴承的多体动力学模型。考虑到轴承转速较低,忽略轴承自身的阻尼大小及旋转刚度,采用等效刚度的非线性弹簧来进行代替轴承静态刚度。通过拟静力学计算得到轴承的等效刚度曲线如图2 所示。
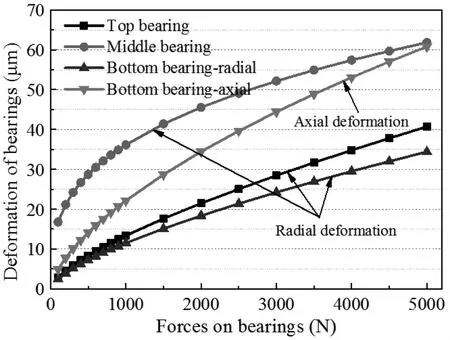
图2 轴承刚度曲线图
1.2 丝杠等效原则
由于丝杠的螺纹结构,其在划分网格及计算过程中存在较大的影响,因此对丝杠螺纹结构的简化处理是必要的。通过一个光杆(保留啮合区的部分螺纹结构)来代替丝杠进行动态特性研究,改变杆件的直径及密度以保证光杆与丝杠之间刚度及质量的等效,从而保证其模态的等效。通过计算,简化处理的丝杠其等效直径和等效密度分别为26.20 mm 和9.059×103kg/m3。
1.3 转子结构的偏心
细长型丝杠较易发生大变形、振动,甚至不稳定,加之轴承自身磨损,从而导致转子产生偏心的现象。转子的偏心改变了转子与励磁线圈之间的励磁间隙,使得作用在转子上的电磁拉力改变。分布在转子上的径向拉力加剧了轴承的磨损,而轴承的磨损反过来又加剧了转子的偏心,产生了转子偏心与轴承磨损之间的相互耦合。
2 结果与讨论
针对建立的大跨距细长型复合丝杠结构多体动力学模型,本文着重分析在轴承磨损之后导致转子发生偏心的情况下,轴承所受作用力变化及啮合区摩擦力矩的变化情况。
2.1 轴承受力
轴承的受力大小与转子的偏心量直接相关,而转子的偏心量又取决于轴承的磨损厚度。上轴承的单边磨损厚度大于下轴承的单边磨损厚度,中间轴承的磨损厚度取决于上下两个轴承的磨损厚度。同时,轴承的初始间隙大小已包含在轴承磨损厚度中,因此当中间轴承的磨损厚度小于轴承的初始间隙时,需要使用初始间隙代替磨损厚度。
图3 为转子的偏心距对轴承作用力的影响,图中使用上轴承的磨损厚度大小δ1 来表示转子的偏心程度。从图中可以看到,对于上下两个轴承,其轴承力随着偏心距的增加而迅速增加,表明了转子的偏心与轴承受力相互影响,形成恶性循环,使得轴承的工作条件更加恶化。其主要的原因是转子的偏心产生了额外的径向磁拉力,其作用于轴承上,加速了轴承的磨损。中间轴承的作用力并未呈现随偏心距的增加而增加,主要原因是中间轴承的磨损厚度与上下轴承的磨损厚度相关。
2.2 滚轮-丝杠啮合区摩擦力矩
图4 为转速对啮合区摩擦力矩大小的影响。从图中可以看到,啮合区摩擦力矩随转速呈现线型增加,且偏心距越大,摩擦力矩增加地越快,即转速的增加加剧了单位时间的摩擦损耗。同时可以发现,较小的偏心距产生较大的摩擦力矩,其主要原因是较小偏心距使得接触区接触面积增加所致。
图5 为不同偏心距下摩擦力矩的变化图。可以看到,摩擦力矩随着偏心距的增加呈现先减小后增加的趋势,并且在偏心距达到0.8 mm 左右时,其达到了最小值。当偏心距逐渐增加时,啮合区接触面积开始减小,摩擦力矩逐渐减小。当偏心距再增加时,较大的偏心使得啮合区的接触力迅速增加,进而使得摩擦力矩开始呈现上升趋势。
3 结论
本文通过建立细长型大跨距丝杠结构多体动力学模型,分析了转子的偏析、转速的变化等对轴承作用力和啮合区摩擦力矩大小的影响。通过分析,我们得到以下结论。
(1)转子转速的变化对轴承作用力的影响不大。
(2)偏心对轴承力影响显著,轴承作用力随偏心距的增加而增加。
(3)摩擦力矩随转速的变化呈现线型变化,而随着偏心距的增加呈现先减小后增加的变化趋势,存在摩擦力矩的最小值。
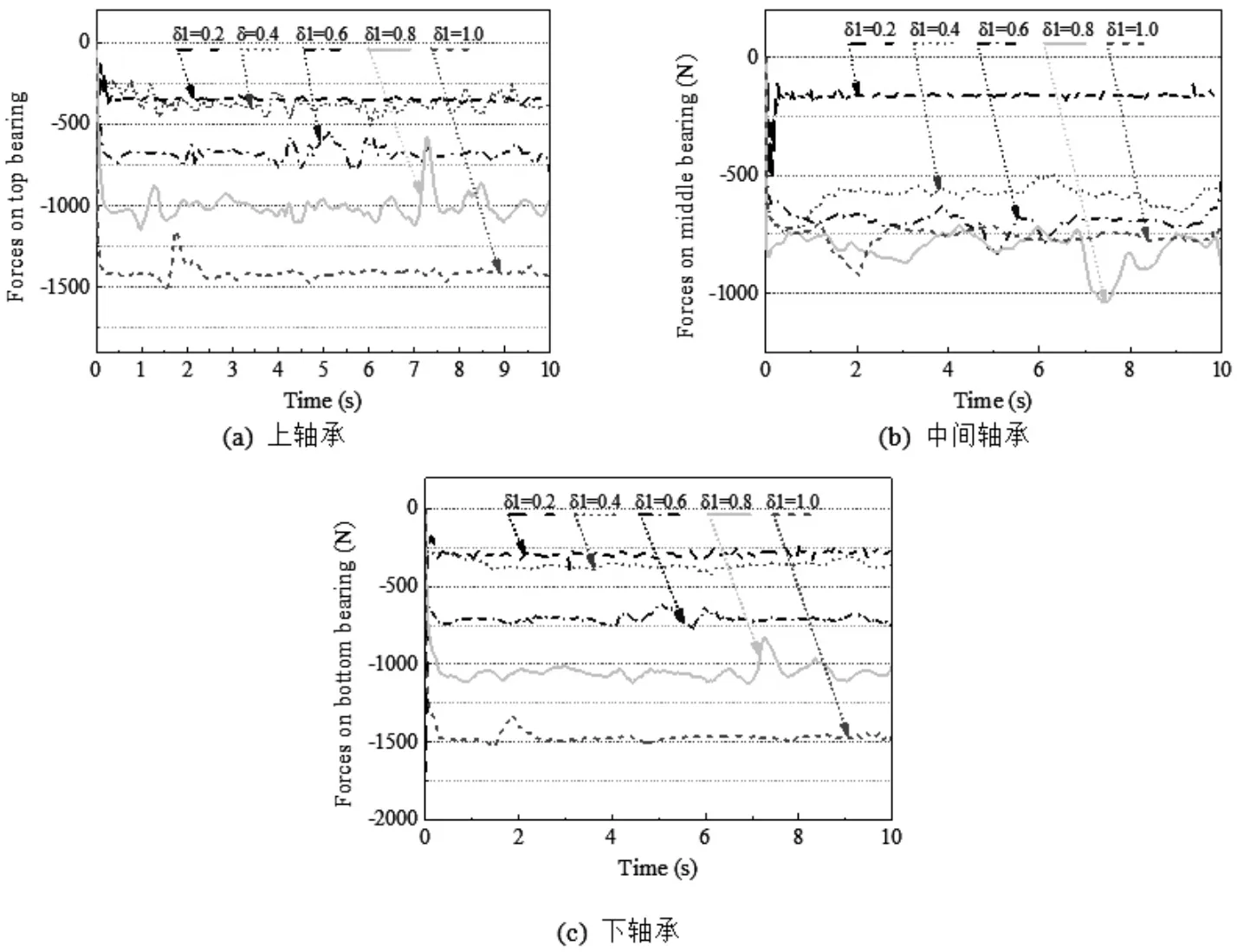
图3 转子偏心距对轴承力的影响
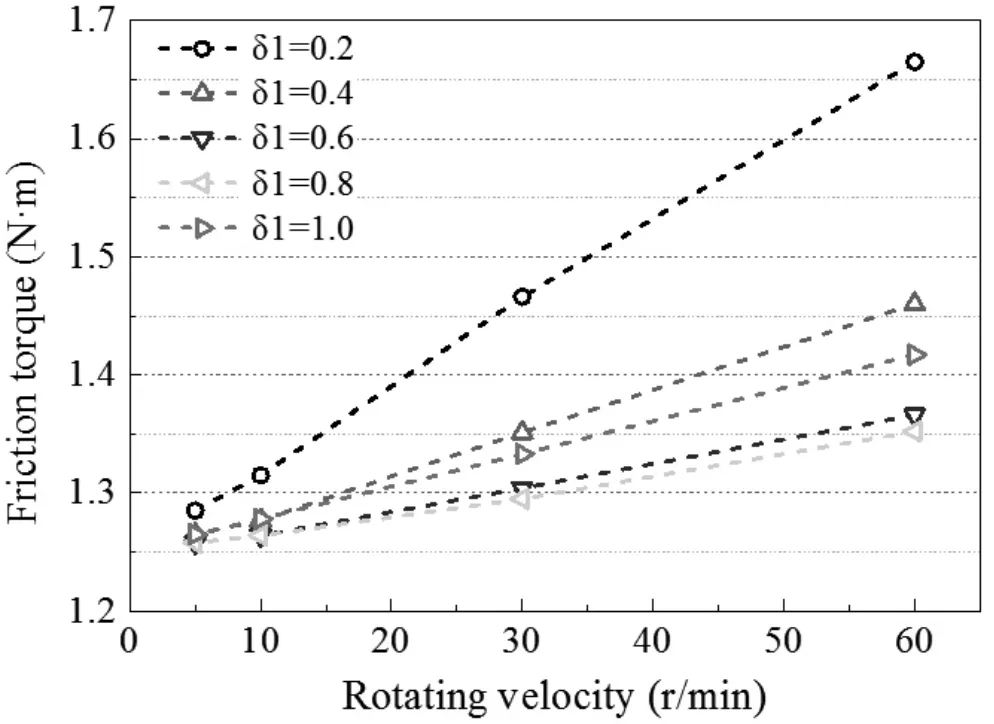
图4 转速对摩擦力矩的影响
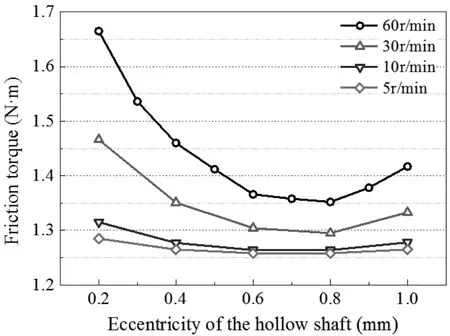
图5 摩擦力矩随偏心距变化
