不同网格加筋壳承载能力比较及影响因素研究

董曼红，胡正根，刘观日，李 斌，阮小鹏

（北京宇航系统工程研究所，北京，100076）

0 引 言

贮箱作为贮存燃料的部段，同时又承受轴向载荷，在火箭设计中起到至关重要的作用。贮箱由前短壳、前底、筒段、后底和后短壳组成，前底、筒段和后底焊接成一个封闭的容器用来贮存燃料，与前后短壳焊接，再通过前后短壳与相邻部段连接[1]。

本文对正置正交网格及等边三角形网格加筋壳筒段在不同直径和内压的承载能力进行分析，得出工程计算方法以及计算结果分析。

1 不同网格加筋壳在运载火箭上的应用

因为火箭结构的特点和载荷方式，贮箱筒段会受到内压、轴向力和弯矩的作用。在贮箱设计中，会对载荷进行综合分析来确定贮箱筒段的设计载荷，以内压作为设计载荷时，筒段会采用光筒结构形式；以轴压为设计载荷，筒段会采用网格形式。

目前国外常用的网格形式主要有正置正交、斜置正交和正置等边三角形网格等。20世纪70年代美国麦道宇航公司针对正置正交网格加筋壳结构的抗扭刚度低、斜置正交加筋壳结构的轴压刚度低等缺点，率先提出了正置等边三角形网格加筋壳结构，其后世界各国开始研究和应用正置等边三角形加筋壳体，例如美国德尔它4、宇宙神5火箭，欧洲阿里安5和日本H2系列运载火箭贮箱均广泛采用三角形网格加筋结构。目前，Φ5 m直径及以下的国外普遍采用正置等边三角形网格，Φ9 m级左右的网格加筋壳普遍采用正置正交网格加筋壳。

中国运载火箭设计中，以轴压为设计载荷的筒段，传统型号一般采用化铣的斜置正交结构，随着技术的发展，在新型运载火箭设计中，为了提高结构承载效率，降低结构质量，火箭贮箱壳段网格加筋壳的选择主要集中在正置正交网格壳和等边三角形网格壳[1,2]。

为了给贮箱筒段设计提供正确的设计依据，需要对正置正交网格壳和等边三角形网格壳进行计算方法的确认以及分析。贮箱及筒段结构如图1、2所示。

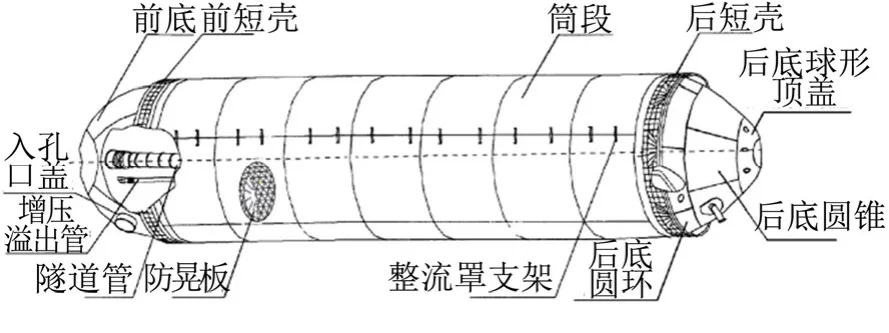
图1 贮箱结构示意Fig.1 Tank Structure

图2 筒段结构示意Fig.2 Tube Structure

2 不同网格加筋壳承载能力计算方法

2.1 计算方法

等效刚度法（Equivalent Stiffness Method，ESM）是一种针对加筋筒壳结构的解析等效方法，是传统的加筋筒壳结构抹平方法，对于加筋单胞构型复杂的情况难以实现准确解析公式，而且筋条只能承受轴向载荷的假设导致其分析结果误差较大。针对轴内压工况网格加筋筒壳，为了获得高效率、高精度的承载能力工程计算方法，通过商业软件实现的快速数值求解方法—渐近均匀化方法（Novel Numerical Imрlementation of Asymрtotic Homogenization Method, NIAH），在计算三维和二维周期性微结构的材料等效性质方面已经具有成熟的理论和算法，计算方法的有效性已被蔡园武和程耿东等人验证[4]。本文采用渐近均匀化方法作为工程计算方法，对网格加筋壳筒段进行分析计算。这种计算方法针对于加筋筒壳结构，计算流程为：

a）从加筋筒壳中划分出代表性单胞结构，建立其有限元模型；

b）基于渐近均匀化方法计算单胞结构的等效刚度系数Aij、Bij和Dij；

c）将上述等效刚度系数代入瑞利-里兹公式，计算得出整体型屈曲载荷值和屈曲模态波数。

传统计算方法[5]计算A、B、D矩阵是简化后的计算结果，而这种快速数值求解方法利用有限元强大的计算程序。把网格按照循环对称划分，只精确计算局部单胞的A、B、D矩阵，再代入工程计算，优点有：a）A、B、D矩阵精确；b）适合各种循环网格，可以把正置正交网格、竖三角形网格和横三角形网格合成集合计算，同时可以计算筋条不等宽的网格加筋壳的承载能力。

2.2 快速数值求解方法精度验证

2.2.1 算例验证

以典型竖置三角网格加筋壳为例，验证这种计算方法的精度。模型几何参数如下：网格加筋壳直径为Φ4000 mm，网格加筋壳高度L=6000 mm，蒙皮厚度ts=5.5 mm，壁板高度H=50 mm，筋条宽度tw=13 mm，筋条间距bs=135 mm。基于商用软件AВAQUS建立网格加筋壳有限元模型，采用四节点壳体减缩积分单元S4R进行离散，蒙皮处的单元尺寸选为50 mm，筋条高度方向划分两个单元。设置简支边界条件，并基于子空间法计算线性屈曲载荷。有限元算法所得失稳波形如图3所示，快速数值求解方法、线性有限元方法和等效刚度法的承载力计算结构的对比如表1所示。

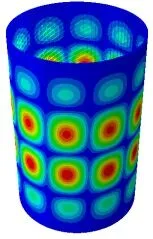
图3 整体失稳示意Fig.3 Вucking Instability

表1 失稳模式及计算时间对比Tab.1 Table of Instability Mode and Calculation Time

由表1可知，针对该模型，有限元法计算耗时960.37 s，得出的屈曲载荷为146 834 kN，环向半波数为9，纵向半波数为4；快速屈曲分析方法耗时21.92 s，计算得出的屈曲载荷为152 572 kN，其相较于有限元法的等效误差为3.76%，环向半波数为9，纵向半波数为4；采用等效刚度分析方法耗时3.18 s，计算得出的屈曲载荷为157 029 kN，其相较于有限元法的等效误差为6.94%，环向半波数为10，纵向半波数为2。

对比这 3种算法可知：快速数值求解方法相较于有限元方法，屈曲载荷计算结果仅差 3.76%（等效刚度分析方法等效误差为 6.94%），计算效率提高了 44倍，同时捕捉到轴向屈曲半波数与环向屈曲半波数与有限元结果相同；快速数值求解方法相较于等效刚度法，计算精度更高，同时捕捉到的轴向屈曲半波数与环向屈曲半波数更精准。

快速数值求解方法与传统的等效刚度法的等效刚度阵中的A阵基本一样，B阵和D阵相差较大。这是因为传统的等效刚度法对筋条进行等效，难以准确描述筋条与蒙皮之间的耦合关系。快速数值求解方法与传统等效刚度法的A、B、D阵误差分析如表2所示。

表2 快速数值求解方法与传统等效刚度法的ABD阵误差分析Tab.2 AВD Matrix Error of NIAH and ESM

2.2.2 样本比较

针对数值模型的设计变量，抽取 100个采样点计算，运用快速数值方法和等效刚度法对其进行计算，快速数值求解方法较有限元方法的相对误差均在 10%以内，其中81个样本点的相对误差在5%以内；等效刚度法较有限元方法有94个样本点的相对误差在10%以内，有6个采样点的相对误差超过10%，最大误差可达40.23%。说明快速数值求解方法更能准确地计算网格加筋壳的承载能力，可以用于新型运载火箭中贮箱筒段的设计。

3 不同网格加筋壳直径和内压对承载能力的影响

3.1 不同网格加筋壳算例确定

网格加筋壳优化条件为：a）弹性模量E=68 246 MPa，泊松比υ=0.33，屈服强度σs=363 MPa，极限强度σb=435 MPa，密度ρ=2.7×103kg/m3；b）载荷为纯轴压载荷；c）直径为Φ9500 mm。

快速数值求解方法的优化目标：筒段长度12 000 mm，质量8000 kg左右，承载能力最大。有限元分析方法的优化目标：筒段长度12 000 mm，质量14 700 kg左右，承载能力最大。网格加筋壳的优化结果如表3、4所示，后文的计算结果均基于这组网格参数。

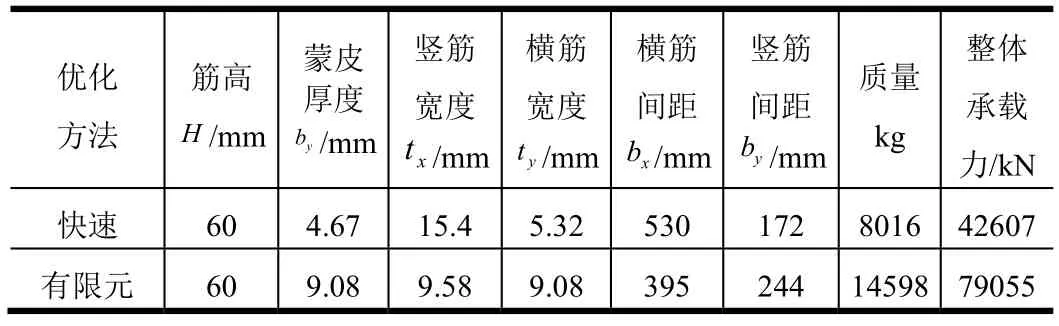
表3 正交正置网格优化结果Tab.3 Oрtimization Results of Orthogonal Mesh

表4 等边三角形网格优化结果Tab.4 Oрtimization Results of Eрuilateral Triangular Mesh

3.2 快速分析方法计算结果

正交正置网格筒段各个直径筒段在网格参数相同的情况下，纯轴压作用下，承载能力相当，直径关系不大；内压对承载力有好处，内压越大，承载能力越大，而且随着直径减小，内压的好处随着减小。

三角形网格筒段在纯轴压载荷作用下，竖置三角型网格筒段相对横置三角形网格筒段有优势，但是优势不大；在网格参数相同的情况下，内压和直径对承载能力影响不大，与纯轴压承载能力相当。

3.3 有限元分析结果

a）模型说明。

贮箱包括前后底、筒段和前后短壳，筒段只是贮箱的一部分，为了准确模拟边界条件，有限元模型由前后底、前后短壳和筒段组成。筒段作为关键模型，高度为12000 mm；前后短壳高500 mm，前后底为椭球结构，短壳和前后底给出足够刚度，保证不先与筒段失稳，筒段材料为铝合金2219。

b）模型边界条件。

有限元模型为4节点壳单元（单元节点有3个平动自由度和3个转角自由度），采用显式动力学对筒壳结构进行非线性后屈曲分析。

轴压作用时，约束下端面所有自由度和上端面除轴向外的其他5个自由度；内压和轴压作用时，约束下端面所有自由度和上短壳除轴向其他5个自由度，内压和轴压分两个步骤施加：a）施加内压，内压初步取 0.1 MPa；b）以位移的形式施加轴压，总位移为120 mm，根据轴压时筒壳力位移曲线获得网格加筋筒壳结构的极限承载力，从而计算得到承载效率。

c）结果分析。

正交正置网格筒段：在网格参数相同的情况下，纯轴压作用下，承载能力随直径的减小而减小；直径不大于Φ3350 mm时，内压对承载能力几乎没有影响；直径大于Φ3350 mm时，承载能力随内压的增加先增加后减小，直径不小于Φ7000 mm时，下降速度加快；快速分析方法计算中给的是整体失稳，所以失稳载荷几乎不变，而有限元中给的是蒙皮筋条整体先失稳的载荷，随直径增加而增大，与前文分析一致。

三角形网格筒段，竖置和横置变化趋势一致：在网格参数相同的情况下，纯轴压作用下，承载能力随直径的减小而减小；当直径不大于Φ3350 mm时，内压对承载能力几乎没有影响；当直径大于 Φ3350 mm时，承载能力随内压得增加而下降，当直径不小于Φ7000 mm时，下降速度加快；三角形网格与正交正置网格筒段相比较，除正交正置网格筒段在直径大于Φ3350 mm时随着内压增加有一段先升后降的趋势外，其余变化趋势一致，而这个内压在0～0.3 MPa之间。

3.4 直径和内压对不同网格加筋壳承载能力的影响

3.4.1 纯轴压作用

工程计算结构承载能力与直径关系不大，而有限元与直径关系密切，这是因为：a）工程计算中计算结果是总体失稳载荷，而有限元计算的是整体失稳载荷、蒙皮失稳载荷、筋条失稳载荷的最小值。有限元模型Φ9500 mm直径，对结构参数进行优化，整体先失稳，蒙皮和筋条后失稳，而随着直径的减小，网格参数没有变化，导致蒙皮和筋条先失稳，这样，随着直径的减小，承载能力减小；b）工程计算是线性计算，而有限元给的是非线性计算结果。

为此，选取正交正置网格筒段进行各个直径下的承载能力计算：a）利用快速分析方法计算整体失稳载荷、蒙皮失稳载荷、筋条失稳载荷。在网格参数不变的情况下，整体失稳载荷随直径变化不大，而蒙皮和筋条失稳载荷随直径的减小而减小。取最小承载能力后，结果与有限元结果趋势一致。b）对相同网格参数进行有限元的线性计算，当直径大于Φ6000 mm时，工程方法与线性有限元法的结果基本相同；当直径在Φ3350～5000 mm之间，计算结果相差10%以内；当直径小于Φ3350 mm时，相差较大。这是因为各个直径下，筒壳长一致保持12 m，直径过小会导致结构由中长壳变为长壳而使结果不够准确，这个问题可以通过更改模型长度解决。c）结果进一步证明，快速分析方法应用于初步设计是合理的，大直径加筋壳筒段更适合这种快速分析方法。

3.4.2 轴压和内压联合作用

正置正交网格网格加筋壳筒段快速数值求解方法计算结果是：内压对轴压承载能力有好处，直径越大，好处越大；有限元计算当直径小于等于Φ3350 mm时，内压对承载能力几乎没有影响，直径大于Φ3350 mm时，承载能力随内压的增加先增加后减小；在小内压大直径时，工程计算和有限元计算结果变化趋势一致。

三角形网格加筋壳筒段，竖置和横置三角形网格变化趋势一致。快速分析方法计算结果是：内压和直径对承载能力影响不大，与纯轴压承载能力相当；有限元分析结果是当直径小于等于Φ3350 mm时，内压对承载能力几乎没有影响，当直径大于Φ3350 mm时，承载能力随内压得增加而下降，当直径大于等于Φ7000 mm 时，下降速度加快；也就是说，在小直径时，工程计算和有限元计算结果变化趋势一致。

为了比较两种计算方法计算结果，确保计算结果正确。对Φ9500 mm直径下的正置正交网格加筋壳筒段进行线性有限元计算，并与快速数值求解方法进行比较，如图4所示。

图4 正置正交网格快速分析方法和线性有限元计算结果对比Fig.4 Load-bearing Ability of Orthogonal Grid NIAH and Linear Finite Element

由图4可知，有限元线性计算结果与工程计算结果变化一致。因为在纯轴压下结构已发生塑性失稳，随着内压增加，内压带来的初始应力越大，快速分析方法只能考虑线性屈曲，无法识别非线性塑性失稳，导致两种方法对规律总结不一致。因此建议采用快速数值求解方法确认结构初步网格参数，根据各工况设计载荷进行非线性有限元计算复核结构承载能力。

3.5 扭矩对不同网格加筋壳承载能力的影响

正置正交网格及等边三角形网格加筋壳承载力随扭矩的变化如图5所示。在扭矩逐渐增大的过程中，加筋筒的承载力都在减小；正置正交网格承载能力直线下降，等边三角形网格加筋壳筋壳在小于 20 kN·m时，下降缓慢。因此，在扭距小于20 kN·m时，推荐采用三角形网格加筋壳设计。

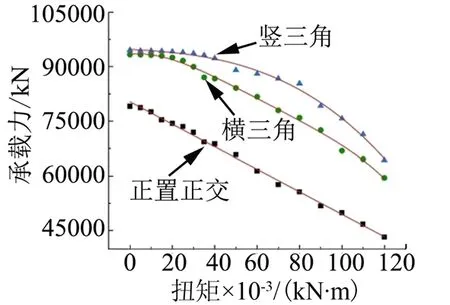
图5 网格加筋筒承载力随扭矩的影响Fig.5 Load-bearing Ability of Grid Reinforced Shell with Rejection

3.6 不同网格加筋壳承载能力比较

网格参数是在纯轴压Φ9500 mm直径下进行优化的，因此，对Φ9500 mm直径3种网格的承载能力进行数值分析。快速数值求解方法计算结果和有限元计算结果都表明：纯轴压作用下，三角形网格加筋承载力优于正置正交网格加筋筒，其中竖置等边三角形网格加筋壳承载效率稍优于横置等边三角网格加筋筒的承载效率。但根据有限元计算，正置正交网格加筋壳在小内压作用下，承载能力会有较小的增加，而等边三角形网格加筋壳承载能力下降，因此，小内压作用下，正置正交网格及等边三角形网格加筋壳承载能力的大小，还需要根据具体载荷进行进一步的确认。

4 结 论

为了对大直径贮箱筒段工程计算方法进行确认分析，本文对正置正交网格及等边三角形网格加筋壳筒段计算结果进行分析研究，分析了直径和内压对网格筒段承载能力的影响：a）直径小于等于Φ3350 mm，工程计算采用线性计算：正置正交网格内压对承载能力有好处，但变化趋势缓慢，非线性有限元计算结果内压增加承载能力变化不大；竖直和横置等边三角形网格工程计算和非线性有限元计算结果都是内压增加承载能力变化不大。b）直径大于Φ3350 mm，工程计算采用线性计算，正置正交网格内压对承载能力有好处，但变化趋势缓慢，三角形网格几乎不变；而非线性有限元计算中随着内压的增加，正置正交网格先升后降，三角形网格则下降。进而说明，通常认为的内压对承载能力有好处是存在一定的条件的。c）正置正交网格及等边三角形网格加筋壳承载力随扭矩的增加而减小，但等边三角形网格加筋在扭距小于 20 kN·m时下降趋势缓慢，因此在扭距较小时，推荐采用等边三角形网格加筋壳设计。