硅光子晶体结构参数对其带隙宽度影响分析

王婷婷 杨运兴 李支新 孙晶

摘  要：借助光子晶体的理论知识和平面波展开法理论方法，依托Matlab、Comsol等计算分析软件，分析了二维三角晶格硅光子晶体结构参数对带隙宽度的影响。就基元形状与旋转角度等结构参数调整对光子带隙宽度的影响进行模拟以及研究。结果发现，在一种固定晶格的光子晶体中，其他条件为定量时，基元形状所占的空间比例越大，光子带隙显现出的结构越好;基元面积固定时，其旋转角度的改变只和带隙宽窄有关，而对带隙的中心频率无影响，或者影响不大。

关键词：硅光子晶体;二维三角晶格;结构参数;带隙宽度;平面波展开法

中图分类号：O734 文献标志码：A         文章编号：2095-2945（2020）24-0020-03

Abstract： Based on the theoretical knowledge of photonic crystals and the theoretical method of plane wave expansion method， the influence of the structural parameters of two-dimensional triangular lattice silicon photonic crystals on the band gap width is analyzed by using Matlab， Comsol and other kinds of calculation and analysis software. The influence of structural parameters such as element shape and rotation angle on photonic band gap width is simulated and studied. The results show that in a fixed lattice photonic crystal， when other conditions are quantitative， the larger the proportion of space occupied by the primitive shape， the better the structure of the photonic band gap appears; when the element area is fixed， the change of its rotation angle is only related to the width of the bandgap， but has no or little effect on the center frequency of the band gap.

Keywords： silicon photonic crystal; two-dimensional triangular lattice; structural parameter; width of the bandgap; plane wave expansion method

1 概述

目前电子领域发展面临集成和微型化极限，颇难突破瓶颈，急需通过选择其他有良好性能且符合需求的器件材料实现性能提升[1-2]。在经过大量的尝试和探索后发现，硅基光子晶体有以下几点特性：一是损耗低;二是成本少;三是能效高;四是易制备。因此，这类晶体凭借其多种优良的特性得以发展[3]。

光子晶体内部光子受到周期性的约束和影响，且其具有光子带隙[4-6]（photonic band gap，PBG）。PBG中是禁止任何光入射并传播的，其对于光子晶体掌控光的能力起决定性作用，它的宽度越宽，表明光子晶体掌控光的频域范围越大。针对此，结构参数是PBG的一个重大影响因素，通过对预先设计好的光子晶体结构改变参数变量并不断优化，得到更为理想的PBG，从而达到满足高集成、小尺寸的工艺目标。但面对硅光子晶体器件结构的设计和应用以及实现部分功能的问题上，由于缺乏相关结构参数的理论研究分析，研究过程显得尤为缓慢[7-8]。

本文首先通过光子晶体的理论基础和平面波展开法，建立了二维三角晶格硅光子晶体模型;定量分析了三角晶格内基元形状以及旋转角度等结构参数因素对其带宽的影响;最后总结了模拟计算得出的结果分析并对今后实验研究提供一定的参考依据。

2 理论方法

3 数值分析

3.1 计算模型

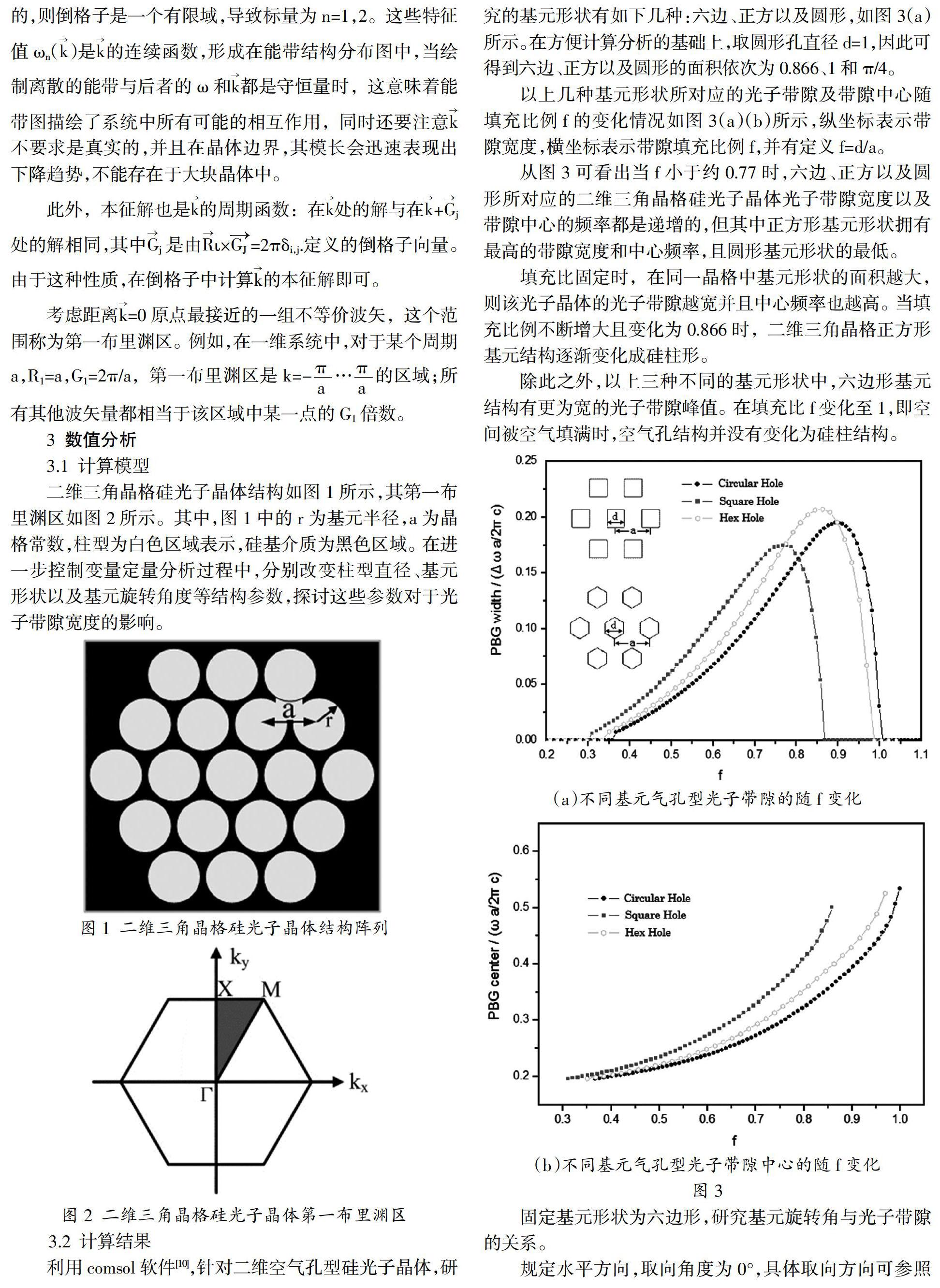
二维三角晶格硅光子晶体结构如图1所示，其第一布里渊区如图2所示。其中，图1中的r为基元半径，a为晶格常数，柱型为白色区域表示，硅基介质为黑色区域。在进一步控制变量定量分析过程中，分别改变柱型直径、基元形状以及基元旋转角度等结構参数，探讨这些参数对于光子带隙宽度的影响。

3.2 计算结果

利用comsol软件[10]，针对二维空气孔型硅光子晶体，研究的基元形状有如下几种：六边、正方以及圆形，如图3（a）所示。在方便计算分析的基础上，取圆形孔直径d=1，因此可得到六边、正方以及圆形的面积依次为0.866、1和π/4。

以上几种基元形状所对应的光子带隙及带隙中心随填充比例f的变化情况如图3（a）（b）所示，纵坐标表示带隙宽度，横坐标表示带隙填充比例f，并有定义f=d/a。

从图3可看出当f小于约0.77时，六边、正方以及圆形所对应的二维三角晶格硅光子晶体光子带隙宽度以及带隙中心的频率都是递增的，但其中正方形基元形状拥有最高的带隙宽度和中心频率，且圆形基元形状的最低。

填充比固定时，在同一晶格中基元形状的面积越大，则该光子晶体的光子带隙越宽并且中心频率也越高。当填充比例不断增大且变化为0.866时，二维三角晶格正方形基元结构逐渐变化成硅柱形。

除此之外，以上三种不同的基元形状中，六边形基元结构有更为宽的光子带隙峰值。在填充比f变化至1，即空间被空气填满时，空气孔结构并没有变化为硅柱结构。

固定基元形状为六边形，研究基元旋转角与光子带隙的关系。

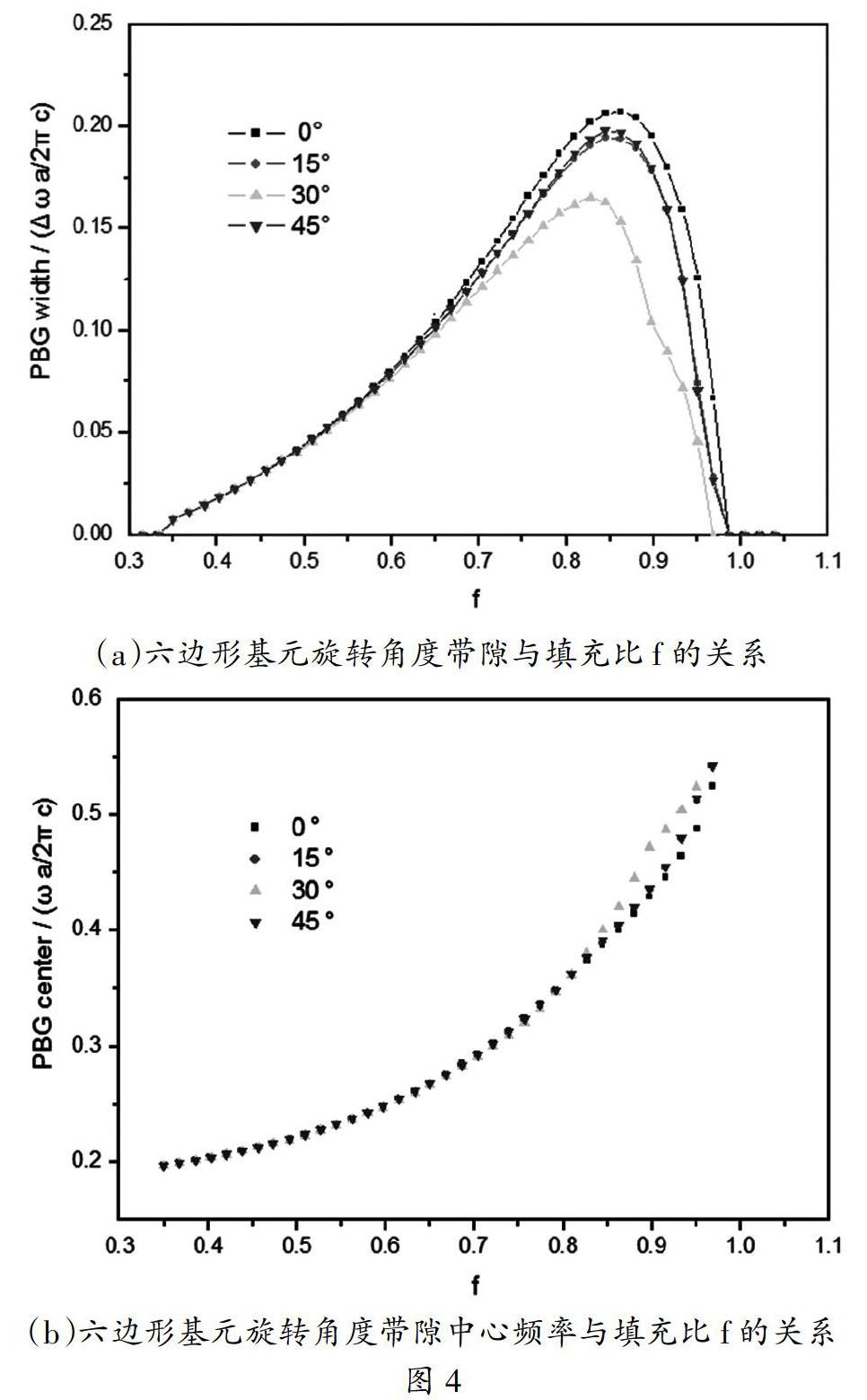
规定水平方向，取向角度为0°，具体取向方向可参照图3（a）。研究在旋转角度分别为0°、15°、30°以及45°时带隙宽度随着填充比f的关系。计算结果如图4（a）所示，可看出，六边形基元的带隙宽度随旋转角度变化既满足旋转对称性以及周期性又同时有各向异性。0°旋转角，任何填充比对应的光子带隙宽度都为最大值，可认为旋转角为0°时，是六角形基元对于二维三角晶格的最优取向。

图4（b）是六边形基元在不同旋转角度时，带隙中心随着填充比f的变化关系。从图中可看出，在基元面积不变的情况下，带隙中心频率基本相同，基元旋转角度的改变对该结构中光子的束缚能力没有变化。

4 结论

在微电子领域面临提高集成度、运行效率，降低损耗和成本的背景下，硅光子晶体得到大量且广泛的研究，使得相关技术的突破成为可能。而光子带隙作为光子晶体中尤为重要的一大特性，对实现硅光子器件的优化升级有极其重要的作用。本文通过计算软件模拟了二维三角晶格硅光子晶体的物理模型，对基元形状做出调整，分析了六边、正方以及圆形形状对于光子带隙宽度及带隙中心频率的影响;在一种固定晶格的光子晶体中，其他条件为定量时，基元形状所占的空间比例越大，光子带隙显现出的结构越好。在填充比例变大的过程中，基元的取向固定的条件下，基元形状为六边形的二维三角晶格硅光子晶体带隙表现更加优秀。因此，在实验研究过程中，建立在结构上，可通过充分的填充来更好地实现对光子的控制，对今后的研究应用有指导意义。

参考文献：

[1]Kapil Debnath，Marco Clementi，Thalía Domínguez Bucio，et.al.Ultrahigh-Q photonic crystal cavities in silicon rich nitride[J]. Optics Express，2017，25（22）：27334.

[2]Yi L，Xiaohai B，Dongxian L，et al.Research Progress of Infrared Stealth Materials Based on Photonic Crystals[J]. Laser &Optoelectronics Progress，2019，56（8）：080003.

[3]Ruda H E，Matsuura N.Properties and applications of photonic crystals[J].Optical Properties of Materials and Their Applications， 2019，30（6）：251-268.

[4]Guo Y，Pu M，Ma X，et al.Advances of dispersion-engineered metamaterials[J].Opto-Electronic Engineering，2017，44（01）：3-22.

[5]陈义万，杜海霞，陈昭蓉，等.二维光子晶体带隙与结构的关系[J].湖北大学学报（自科版），2016，38（3）：19.

[6]Limei Qi，Ziqiang Yang，Xi Gao，等.Analysis of two-dimensional photonic band gap structure with a rhombus lattice[J].中國光学快报（英文版），2008，6（4）：279-281.

[7]方云团.光子晶体计算方法和传输特性[J].安庆师范大学学报：自然科学版，2019，17（2）：16.

[8]蔡青，黄昌清，梁培，等.基于平面波展开法的二维光子晶体表面模式研究[J].光子学报，2012，041（4）：430-435.

[9]黄晓泽，周琦，饶黄云.利用平面波展开法在matlab中计算一维光子晶体的带隙结构[J].科技创新与应用，2019，9（13）：29-31.

[10]邱伟彬，林志立.利用COMSOL仿真进行二维光子晶体的教学[J].高教学刊，2019，5（7）：66-69.