基于改进k-均值聚类方法的风电场解析模型

李从飞 侯继海 史杰 张乐涛

摘  要：风电场解析模型的建立是利用解析法或非序贯蒙特卡洛模拟法进行发电系统充裕度评估的基础。提出了利用改进的k-均值聚类算法建立多级水平风电场概率模型;利用解析法对RBTS可靠性测试系统进行了算例分析。算例结果表明，基于所提出的聚类算法得出的风电场概率模型具有很高的计算精度和收敛速度，适合用于风电并网发电系统的充裕度评估。

关键词：风电场;概率模型;k-均值聚类;充裕度;解析法

中图分类号：TM712 文献标志码：A         文章编号：2095-2945（2020）24-0007-04

Abstract： The establishment of wind farm analytical model is the basis of evaluating the generation system adequacy when the enumeration method or non-sequential Monte Carlo method is employed. The improved k-means clustering method is proposed to model the multi-step wind farm output power probabilistic characteristic. The proposed modeling algorithm is validated in the RBTS by enumeration method. Case studies indicate that the wind farm models from the proposed algorithm has high calculation accuracy and convergence speed， and is appropriate for the generating adequacy evaluation containing wind power.

Keywords： wind farm; probabilistic model; k-means clustering method; adequacy evaluation; enumeration method

引言

在传统一次能源日益枯竭、环境问题日渐突出以及各国政府对风电发展的政策扶持的背景下，风力发电在世界范围内得到了快速的发展。同传统发电系统相比，风能具有间歇性和波动性的特点，风电接入系统比例的不断增加将会给电网的安全运行带来极大的挑战。一些学者分别从继电保护[1]、电力系统稳定性[2]、低频振荡[3]、电力系统调度[4]等不同角度研究了风电大规模接入对电力系统的影响，本文从可靠性的角度研究了风电间歇性和随机性对电力系统充裕度的影响。

进行电力系统充裕度评估的方法分成确定性的方法（如常用的N-1准则）和概率性方法两类[5]。确定性的方法具有实现方便的特点，能对系统充裕度作粗略的估计，但是不能反映电力系统行为、负荷变化以及元件故障等方面的概率属性。概率性方法能够统计故障行为发生和负荷变化等不确定性因素带来的影响，能够更科学、更准确地反映电网实际运行状况，從而获得更为准确的可靠性指标。概率性的方法又分为解析法和蒙特卡洛法两类，二者的根本区别在于获取系统随机状态及其概率分布的方法不同，其中蒙特卡洛可以进一步分为序贯和非序贯蒙特卡洛模拟两类。

在利用解析法或非序贯蒙特卡洛模拟法进行风电并网发电系统的可靠性评估时，通常将风电场等值成一个多状态的常规机组[6]，而风电场等值状态数目以及各状态的出力水平的确定对风电场建模的精度有很大的影响。其中风电场等效状态的数目，应该在对计算精度和计算工作量进行综合权衡之后做出合适的选择。文献[7-8]分别采用5状态和6状态的风电场解析模型进行充裕度评估，算例表明这两种风电场多状态模型均具有较高精度，而文献[9]则进一步指出风速状态数目至少是4阶时才能保证较好的精度。因此在本文算例研究中将风电场等值状态的数目确定为6个。

而针对风电场各等值状态出力水平的确定问题，文献[10-12]采用任意指定划分的方法，即首先任意指定风电场各等值状态的出力水平，然后采用线性舍入法将风电场时序出力归类到相应的等值状态出力水平。这种指定划分方法的缺点在于难以选择合适的等值状态出力水平，难以准确反映风电场的概率分布。本文提出利用改进的k-均值聚类技术对风电场输出时序功率进行聚类，利用聚类的方法来建立多状态风电场模型。并根据解析法进行发电充裕度评估的原理，以RBTS测试系统为例进行了算例验证。算例结果表明，采用改进k-均值聚类技术建立的风电场解析模型在进行充裕度评估时具有较高的计算精度。

1 风电场解析模型

1.1 基于划分的风电场概率模型

根据风电场风速时间序列和风电机组的功率特性曲线，可以得到风电场输出功率的时间序列。将每小时的风电场输出功率划分到指定风电场输出功率的水平之后，进行统计计算即可得到各级水平的风电场出力概率。形成风电场概率模型主要包括以下几个步骤：

1.1.1 风电场风速时间序列的获取

通常采用ARMA预测模型或Weibull分布模拟产生某一地区的风速时间序列。本文根据国内某风电场历史实测数据，将威布尔分布参数分别取值为c=8.03，k=2.02时，模拟得出典型的年风速时序图如图1所示。

1.1.2 求取单台风机输出功率的序列值

根据小时风速序列，结合风电机组功率特性曲线，即可得到单台风机的输出功率小时序列值，典型的风电机组功率特性曲线如图2所示。

1.1.3 求取风电场输出功率的概率模型

文献[12]的研究表明风电机组的故障率对系统可靠性指标影响很小，因此本文在进行风电并网电力系统可靠性评估时忽略风电机组的随机停运，由相同类型的风机构成的风电场输出功率时间序列值可以直接由单台风机的输出功率时序值乘以风机台数获得。具体的获取风电场输出功率时间序列的步骤如下：

（1）将风电场出力划分为N个状态，指定各状态的风电场出力水平。

（2）根据风速时序值和风电机组功率特性曲线，计算单台风机输出功率时序值。

（3）计算时序风电场出力，并按照线性舍入法将时序风电场出力划分到各指定状态出力水平中。

（4）统计划分到各状态的时序风电场功率个数，从而得出各状态的概率。

1.2 基于改进k-均值聚类方法的风电场概率模型

采用划分的方式来对风电场出力进行聚类时，对于风电场各出力水平的选取具有主观任意性，选取不当有可能会导致风电场的解析模型精度较差。为了避免风电场出力水平选择过程中的任意性和提高风电场模型精度，考虑采用k-均值聚类算法来建立风电场概率模型。

k-均值聚类方法是划分聚类算法的一个典型的算法[14-15]，它通过不断计算k个类别的聚类中心，并对样本点进行最近距離分类的聚类算法。算法的一般步骤为：首先将所有样本点随机的分为k个类别（其中k是事先指定的类别个数），然后计算每个类别的样本中心点，求取每个样本点与k个中心点的距离并重新归类到距离最近的类别中间。重复上述步骤直到算法收敛或者到指定的迭代次数为止。

k-均值聚类方法属于迭代的方法，当样本数据比较密集、类与类之间的区分特别好的时候， k-均值聚类算法的效果较好。但是当样本数据含有差别很大、带有孤立点数据的类时，聚类效果较差，并且对初始值的选取较敏感。而风电场的风速具有非均匀性的特点，因此对风速初始聚类中心的随机选取有可能会导致得出聚类效果较差的结果。为了避免聚类中心初始值选取不当可能造成聚类结果不稳定、聚类精度不高的问题，本文提出采用基于层次聚类的k-均值聚类改进算法来进行风电场出力的聚类。即先应用层次聚类算法得到一个初始的划分，计算每个类内对象的均值并将它作为k-均值聚类算法的初始聚类中心。这种聚类中心初始化方式能够利用数据中的类结构信息，使得初始聚类中心在空间分布上与数据实际分布相一致，因此聚类质量相对于随机初始化时的平均质量有显著的提高。基于层次聚类改进的k-均值聚类算法的步骤如下[16]：

（1）确定聚类个数k;

（2）对数据集进行层次聚类分析;

（3）根据层次聚类结果的每个对象的标示，将同样标示的数据对象累加在一起，并对数据对象个数计数，得到层次聚类分析后k个类的均值，并将其作为初始聚类中心;

（4）根据每个聚类对象的均值，计算每个对象与这些聚类中心的距离，并将该对象归入离它最近的那个聚类中心所代表的簇;

（5）重新计算每个簇的聚类中心;

（6）重复（4）和（5），直到每个对象所属类不再发生变化为止。

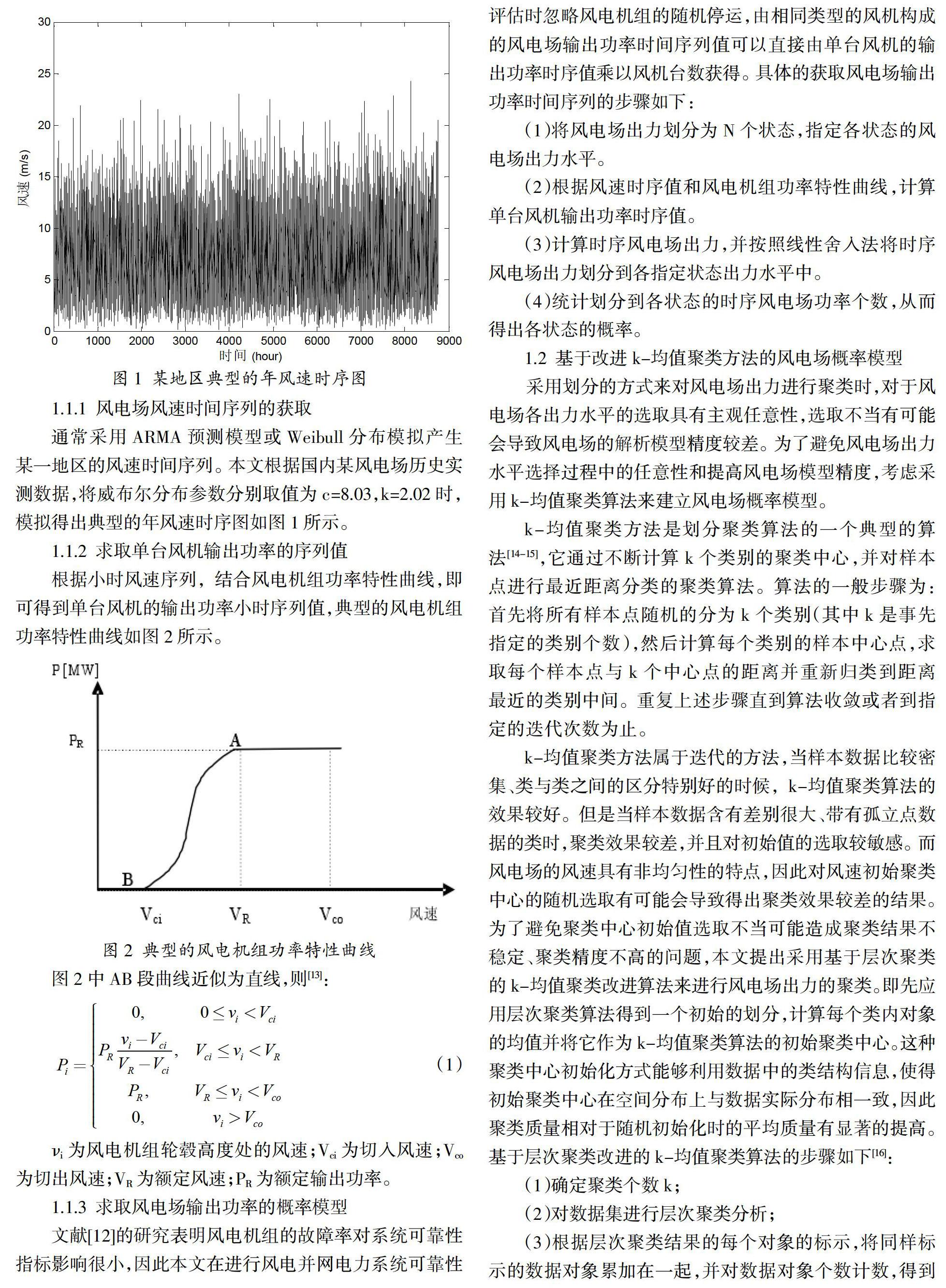
在利用改进k-均值聚类算法对风电场出力序列聚类之前，可以先将风电场出力序列按照递增的顺序排列，这样只需对两个临近的聚类计算距离从而加快了聚类速度。利用改进k-均值聚类算法进行风电场出力序列聚类的流程图如图3所示。

2 解析法计算发电充裕度

在进行风电并网后的发电系统可靠性评估时，可以将风电场等效成一个具有多个降额状态的常规机组，而风电机组处于各个出力水平状态的概率则可通过前述的聚类算法得到。将多降额状态的风电场概率模型同常规机组概率模型相结合，可得出风电并网后的发电系统容量停运概率表;将发电容量和负荷水平概率进行卷积运算，即可得出发电可靠性指标。电力不足时间期望（Loss of Load Expectation，LOLE）、电量不足期望（Loss of Energy Expectation，LOEE）是发电系统充裕度评估中最常用的两种指标，可以通过下面的卷积公式分别求得[17]：

式中，Li是第i级负荷水平，Pi是第i级负荷水平概率，NL是负荷水平分级数，Gj是第j级发电容量，Pj是第j级发电容量的概率，NG是发电容量分级数，T是负荷持续曲线时间总长度。

3 算例分析

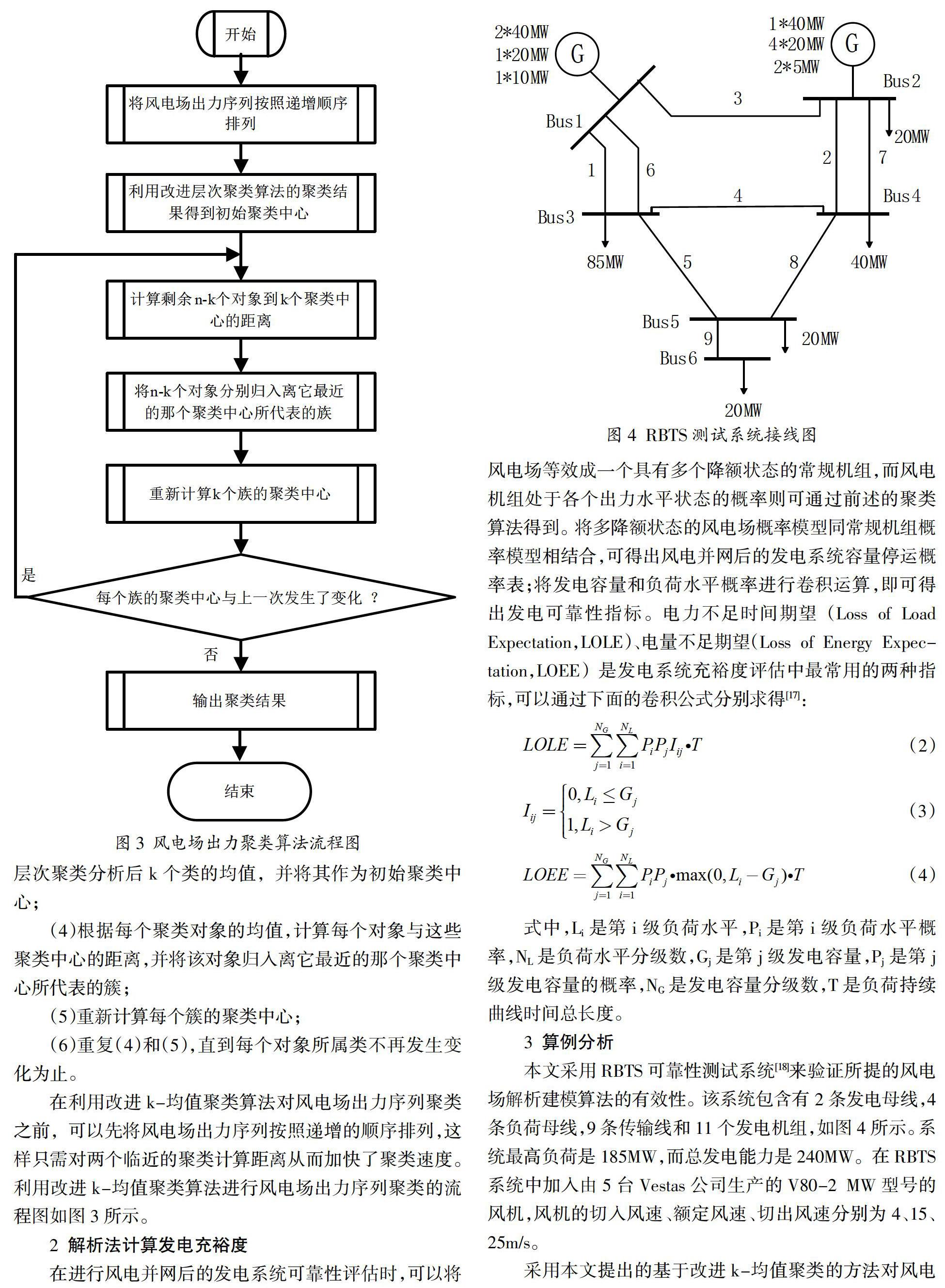
本文采用RBTS可靠性测试系统[18]来验证所提的风电场解析建模算法的有效性。该系统包含有2条发电母线，4条负荷母线，9条传输线和11个发电机组，如图4所示。系统最高负荷是185MW，而总发电能力是240MW。在RBTS系统中加入由5台Vestas公司生产的V80-2 MW型号的风机，风机的切入风速、额定风速、切出风速分别为4、15、25m/s。

采用本文提出的基于改进k-均值聚类的方法对风电场输出功率进行聚类，利用Matlab7.0编制程序，得到10MW风电场多级水平概率模型如表1所示。表1中风电场可用容量的单位为MW。

采用表1中的风电场概率模型，利用解析法计算发电充裕度指标的程序，得到的发电系统LOLE、LOEE指标如表2所示。表2中LOLE以小时/年计，LOEE以MWh/年计，计算时间以秒计。表2中还给出了在不对风电场出力采取任何聚类技术时的充裕度指标。

由表2结果可见，采用改进k-均值聚类所得的风电场解析模型具有较高的计算精度，同时大大地节省了计算时间，适合用于含风力发电的电力系统可靠性评估。

4 结论

本文提出了利用改进k-均值聚类方法建立风电场解析模型的方法，即先对时序功率曲线进行升序排列，然后利用层次聚类算法得到k-均值聚类中初始聚类中心，接着利用k-均值聚类算法得到风电场出力的解析模型。算例结果表明，采用改进k-均值聚类方法能够获得计算精度较高的风电场可靠性模型，适合用于采取解析法或非序贯蒙特卡洛方法进行电力系统充裕度评估时的风电场的概率建模。

参考文献：

[1]韩璐，李凤婷，王春艳，等.风电接入对继电保护的影响综述[J].电力系统保护与控制，2016，44（16）：163-169.

[2]何廷一，李胜男，吴水军，等.大规模风电接入对电力系统暂态稳定风险的影响研究[J].电测与仪表，2017，54（20）：17-22.

[3]杨悦，李国庆.大规模风电并网对互联电力系统低频振荡影响研究[J].太阳能学报，2017，38（10）：2665-2674.

[4]卢锦玲，张津，丁茂生.含风电的电力系统调度经济性评价[J].电网技术，2016，40（8）：2258-2264.

[5]孙腾飞，程浩忠，张立波，等.基于改进混合抽样与最小切负荷计算的电力系统可靠性评估方法[J].电力系统保护与控制，2016，44（13）：96-103.

[6]王森，仉志华，薛永端，等.风电场多状态出力的概率性评估[J].太阳能学报，2016，37（6）：1611-1616.

[7]Billinton R， Yi G.Multistate Wind Energy Conversion System Models for Adequacy Assessment of Generating Systems Incorporating Wind Energy[J].Energy Conversion，IEEE Transactions on，2008，23（1）：163-170.

[8]Karki R， Po H， Billinton R.A simplified wind power generation model for reliability evaluation[J].IEEE Transactions on Energy Conversion，2006，21（2）：533-540.

[9]Mehrtash A， Peng W， Goel L.Reliability evaluation of restructured power systems with wind farms using Equivalent Multi-State models[C].2010.

[10]Liang W， Jeongje P， Jaeseok C， et al.Probabilistic reliability evaluation of power systems including wind turbine generators using a simplified multi-state model： A case study[C].Calgary， AB：2009.

[11]汪海瑛，白曉民.大规模风电场的发电充裕度与容量可信度评估[J].电网技术，2012，36（6）：200-206.

[12]Dobakhshari A S， Fotuhi-Firuzabad M.A Reliability Model of Large Wind Farms for Power System Adequacy Studies[J].Energy Conversion， IEEE Transactions on，2009，24（3）：792-801.

[13]祝锦舟，张焰，杨增辉，等.一种含风电场的发电系统可靠性解析计算方法[J].中国电机工程学报，2017，37（16）：4671-4679.

[14]邵必林，边根庆，张维琪，等.采用k-均值聚类算法的资源搜索模型研究[J].西安交通大学学报，2012，46（10）：55-59.

[15]杨春蓉，赵小勇.利用改进的最优聚类算法边缘提取方法研究[J].计算机应用与软件，2012，29（12）：295-297，328.

[16]段明秀.层次聚类算法的研究及应用[D].中南大学，2009.

[17]Li W.Risk Assessment of Power Systems： Models， Methods， and Applications [M].2nd ed.New Jersey，USA： Wiley-IEEE Press，2014：560.

[18]Billinton R， Kumar S， Chowdhury N， et al.A reliability test system for educational purposes-basic data[J].IEEE Transactions on Power Systems，1989，4（3）：1238-1244.