基于蒙特卡洛方法的非负矩阵分解初始化

陈红莉

(武汉大学数学与统计学院,湖北武汉 430072)

1 引言

非负矩阵分解(NMF)是1999年由Lee和Seung[1]首次提出的,有着比较广泛的应用,如图像处理[1]、文本聚类[2]和社区发现[3]等.相较于其他的矩阵分解,由于元素的非负性,所以可解释性很强.比如:在处理图像时,负的像素点是没有意义的;在文本聚类时,正值代表文档以一定概率属于某个主题,负值则没有任何实际意义.

非负矩阵分解数学描述如下:给定非负矩阵A∈Rm×n,希望找到两个非负矩阵W∈Rm×k和H∈Rk×n,使得A≈WH.可以通过以下优化问题来找到W和H,

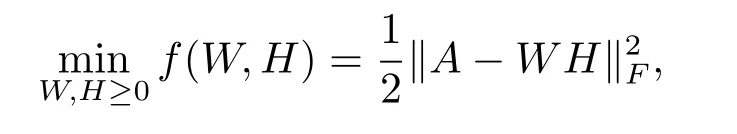
解决非负矩阵分解的方法有很多,比较常见的是由Lee和Seung在2001年提出的基准算法(Multiplicative Update Rules)[4]、Lin在2007年提出的投影梯度法[5]以及Kim和Park在2008年提出的交替非负最小二乘法(ANLS)[6].

不同于某些迭代算法,非负矩阵分解初始值的选择对于算法效果有很大影响.由Qiao提出的SVD-NMF[7]和Boutsidis等人提出的NNDSVD[8]算法都是基于矩阵A的奇异值分解,但是当矩阵A的维数很大时,对A直接进行奇异值分解是耗时的.不同于这两种方法,本文不直接对原矩阵A进行奇异值分解.本文利用Frieze等人[9]的思想,通过抽样构造一个更小的矩阵,对这个小矩阵来做奇异值分解,从而实现对W和H的初始化,这大大节省了算法的计算时间.

2 预备知识

首先,介绍一种最为经典的非负矩阵分解算法,即由Lee和Seung在2001年提出的基准算法(Multiplicative Update Rules)[4],以下简称MU算法.在本文的数值实验部分,将会用到MU算法.MU算法步骤如下

步骤1初始化,∀i,a,b,j.

步骤 2对于k=1,2,···,

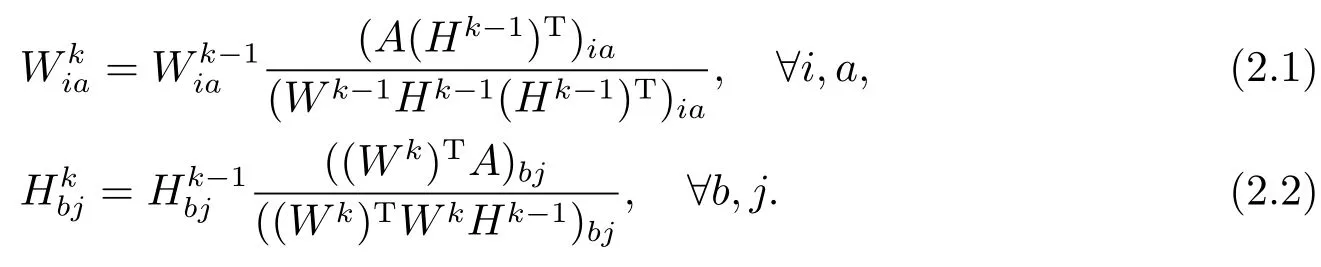
从式子(2.1)和(2.2)中可以看出,如果在第k次迭代中W和H是非负的,那么在第k+1次迭代中,MU算法依然能够保证W和H是非负的.并且,Lee和Seung[4]已经证明在MU算法下,目标函数f(W,H)是非增的,即f(Wk,Hk−1)≤f(Wk−1,Hk−1),f(Wk,Hk)≤f(Wk,Hk−1).

由于本文提出的算法涉及到抽样,下面给出对向量和矩阵进行抽样的假设.

假设2.1[10]给定向量x∈Rn,假设可以根据分布Dx来对i∈{1,2,...,n}进行抽样,也就是说i被抽中的概率为

假设2.2[10]给定矩阵A∈Rm×n,假设满足以下假设

1.可以对矩阵A的行标i∈{1,2,···,m}进行取样,矩阵A的第i行被选中的概率为

2. 对于任意的i∈{1,2,···,m},可以根据分布DA(i,·)来对矩阵A的列标j∈{1,2,···,n}进行抽样,也就是说j被抽中的概率为

定理2.3[9]给定矩阵A∈Rm×n,独立的按照概率分布

从行标中取p个样本:i1,···,ip.记S∈Rp×n为规范化后的子矩阵,即对于t∈{1,···,p},则对于任意给定的θ>0,满足

在第3节,会根据定理2.3说明本文提出的初始化方法(KFV-NMF)的可行性.

3 NMF初始化算法

由定理2.3,可以看出,若按照满足假设2.2的概率分布来抽样:假设抽取了矩阵A的p行,并按照定理2.3所说的构造一个p×n阶的矩阵S,则可以用STS来近似ATA.A的奇异值分解可以通过ATA的谱分解得到,尽管这里可以从STS的谱分解入手,但并不打算这样做,因为STS是一个n×n阶的矩阵,维数也是很大的.这里可以对S的列进行同样的操作,从S中抽取p列,类似的得到一个p×p阶的矩阵W,则WWT近似SST,故最终可以直接对一个p×p阶的矩阵W做奇异值分解,从而近似得到矩阵A的右奇异向量,这大大减少了计算时间.这种思想是Frieze等人[9]提出的,本文借鉴这种思想提出了一种更节时的非负矩阵分解初始化方法,记此算法为KFV-NMF.

下面,给出算法的具体流程.

1 FKV-NMF初始化输入:A,p,k,images/BZ_7_413_771_440_805.png.1.对A的行进行取样:独立的按照满足假设2.2的概率概率分布P=(P1,P2,···,Pm).抽取p个行标,记为i1,i2,...,ip,即Pi=kA(i,·)k2 kAk2.F构造 p × n 阶矩阵 S,其中 S(t,·)=A(it,·)/p pPit,t=1,2,···,p.2.对S的列进行抽样:独立的按照满足假设2.1的概率概率分布P0=(P01,P02,···,P0n).抽取 p 个列标,记为 j1,j2,···,jp,即P0j=pX DA(it,·)(j)/p.t=1 q构造 p × p 阶矩阵 W,其中 W(·,t)=S(·,jt)/pP0 jt,t=1,2,···,p.3.计算矩阵W前k个奇异值ˆσ1,ˆσ2,···,ˆσk以及对应的左奇异向量ˆu1,ˆu2,...,ˆuk.4.构造n×k阶矩阵ˆV:ˆV=(STˆu1ˆσk).5.令W0=max(†,AˆV),H0=max(†,ˆVT).输出:W0和H0.ˆσ1,STˆu2 ˆσ2,...,STˆuk

下面,给出一个定理,并以此来说明算法FKV-NMF中第2步的具体实施方法.

定理3.1假设矩阵A∈Rm×n满足假设2.2,S和W如算法FKV-NMF中第1和2步所构造,则

证由有

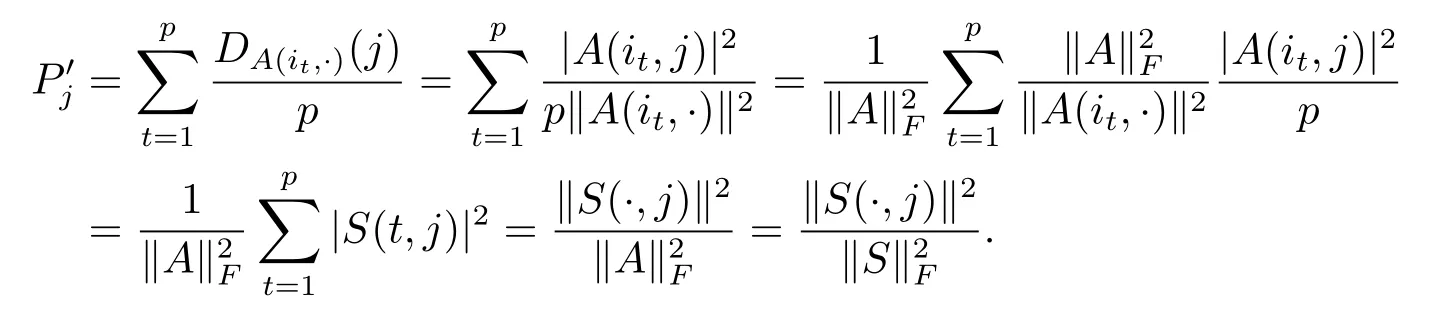
由算法FKV-NMF的流程可以看出,本文提出的初始化算法FKV-NMF的数值计算时间大大减少的原因在于:本文不是对原矩阵A直接进行奇异值分解,而是通过抽样构造一个更小的矩阵W,对小矩阵W做奇异值分解,这使得算法FKV-NMF在奇异值分解上花费的时间大大减少,而现有的基于奇异值分解的初始化算法都是直接对原矩阵A进行奇异值分解,这是本文提出的算法数值计算时间较其他算法减少的原因.另外,通过简单计算可以发现:算法FKV-NMF中矩阵中的每一列可以近似看作矩阵A的右奇异向量,Frieze等人在其文章[9]中也说明了这一点,这也是算法FKV-NMF的理论依据.

当然,算法FKV-NMF也有弊端:此算法虽然在奇异值分解上节省了很多时间,但是它还要计算用于抽样的概率分布P和P0,这是有点耗时的.一般来说,基于奇异值分解的初始化算法使用的都是截断奇异值分解,比如前文提到的初始化算法SVD-NMF和NNDSVD.随着k值的减小,截断奇异值分解所使用的时间也在不断减少,当k小到某一程度时,算法FKV-NMF在进行奇异值分解上节省的时间便不再占优势.但是,这也是算法FKV-NMF可以进一步改进的地方,比如可以考虑使用其他更加快速有效的抽样方法.

4 数值实验

在本次实验中,测试了两组数据:第一组是随机生成的服从均值为0、方差为1的高斯分布的随机数,这里取绝对值来保证矩阵元素的非负性,即A=|N(0,1)|,维数是500×300.第二组是人脸数据库ORL,ORL数据库一共包含400张92×112像素的图片,一共40个人,每人10幅不同表情的脸.在计算不同算法的时间和误差的实验中,将这400张人脸图像组成了一个10304×400的矩阵,作为算法的输入.在进行人脸重构实验时,选取其中360张图像作为训练集,40张图像作为测试集.

在实验中,将本文提出的算法FKV-NMF与两种比较常见的基于SVD的初始化算法SVD-NMF和NNDSVD作了比较.非负矩阵分解算法采用的是经典的MU算法.误差采用公式

在表1和表2中,分别计算了在k等于不同值时,SVD-NMF、NNDSVD和FKV-NMF三种不同的初始化算法所用的时间和所产生的误差.另外,由于本文提出的算法涉及到抽样技术,所以算法效果会有稍许波动,为公平起见,实验重复20次,取平均值.

表1 三种不同的初始化算法所用的时间

表2 三种不同的初始化算法所产生的误差

从表1和表2中,可以看出:就时间来方面说,本文提出的FKV-NMF初始化算法所用的时间要比SVD-NMF和NNDSVD小的多.就误差方面来说,初始化误差比NNDSVD要大一些,但是比SVD-NMF要小.所以本文提出的初始化算法在大大节约了时间的同时,误差也在可接受的范围内.

图1 使用不同初始化算法后,随着迭代次数增加,MU算法误差变化情况

在图1中,展现了SVD-NMF、NNDSVD和FKV-NMF三种不同初始化算法对于非负矩阵分解算法误差的影响.图中曲线表示随着迭代次数增加,误差的变化情况.从图1中可以看出,在使用SVD-NMF、NNDSVD和FKV-NMF三种不同的初始化算法后,使用MU算法进行非负矩阵分解时,随着迭代次数的增加,误差均在减少,直到达到一个平稳值.NNDSVD的初始化误差虽然最小,但误差很快便不再下降.在随机生成的数据(Random)上,大约100次迭代后,误差几乎不再下降,在ORL数据集上,大约200次迭代后,误差几乎也不再下降,而且最终误差比其他两种方法都要高的多.本文提出的FKV-NMF虽然最终误差比SVD-NMF稍高,但是相差并不多.而且在迭代的最初始阶段,使用本文提出的FKV-NMF初始化方法的误差要比SVD-NMF低一些.

下面,展示了使用不同初始化算法后,MU算法迭代次数为1000时,ORL数据库部分人脸图像的重构情况.图2是人脸的重构图像,第1到第3行使用的初始化算法依次是SVDNMF、NNDSVD和FKV-NMF.在表3中,计算了重构图像的信噪比(SNR),第1到第7列分别表示7个重构图像.信噪比是用来衡量图像质量的一种方式,信噪比越大,表示重构的人脸图像质量越好.这里信噪比的计算公式为:其中g(i,j)表示原始图像的灰度值,f(i,j)表示重构图像的灰度值.

图2 ORL数据集人脸的重构图像

表3 重构图像的信噪比(SNR)

从图2和表3中,可以看出:从重构图像的清晰度来看,使用SVD-NMF和本文提出的FKV-NMF初始化算法图像清晰度相差无几,而使用NNDSVD初始化算法的重构图像效果则稍差.从SNR的值来看,使用SVD-NMF和本文提出的FKV-NMF初始化算法图像的SNR值相差并不多,而使用NNDSVD初始化算法的重构图像SNR值要明显小于其他两者.

通过以上数值实验,可以看到:本文提出的初始化算法FKV-NMF的运行时间较SVDNMF和NNDSVD大大减少,也在一定程度上保持了精度.