Hopfield神经网络平衡点的存在性和稳定性
2020-08-13邢青红何景婷
太原师范学院学报(自然科学版) 2020年3期
邢青红,何景婷
(太原工业学院 理学系,山西 太原 030008)
0 引言
神经网络在许多领域都有应用,如模式识别、遥感图像超分辨率识别等,Hopfield神经网络平衡点的存在性和稳定性已有大量研究成果,本文构造新的Lyapunov函数扩大稳定性的条件[1-2].
Hopfield神经网络的模型(1):
(1)
初始条件:xi(s)=φi(s),s∈[-τ,0].τ=max{τji},i,j=1,2,…,n.
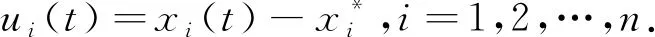
则模型(1)式变为(2):
(2)
(H1)ai>0,bji,cji,Ii∈R,τji∈[0,+∞).
(H2) 行为函数fj:R→R满足lipschz连续,
即
|fj(x1)-fj(x2)|≤hj|x1-x2|,x1,x2∈R
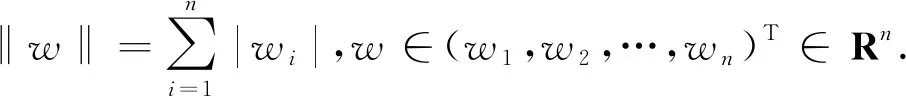
1 平衡解的存在性和稳定性
引理[3]设N是正整数和B是Banach空间,若映射ΦN:B→B是压缩映射,则Φ:B→B在B上有唯一的平衡点.这里ΦN=Φ(ΦN-1).

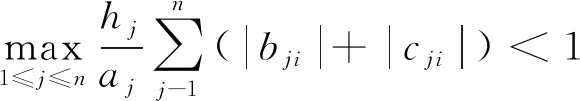

(3)
为了证明(3)式有唯一解,设
Φ:Rn→Rn的映射.

由已知α<1,可得Φ:Rn→Rn是压缩映射,由压缩映射原理知(1)式存在唯一平衡解.
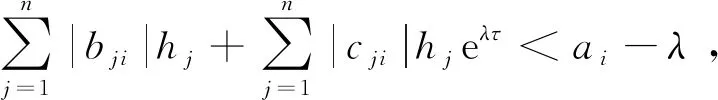
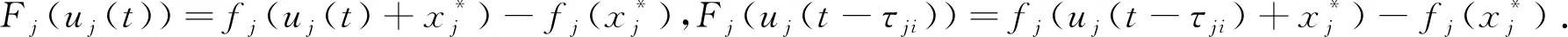
设Lyapunov函数为Vi(t)=|ui(t)|eλt
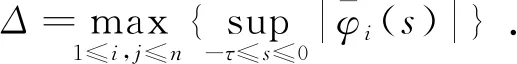
Vi(t1)=Δ.Vi(t)<Δ.对于t∈[0,t1],


可知,当t≥0时,Vi(t)<Δ.