北斗系统QMBOC信号无模糊多径抑制算法研究
2020-08-13王森王雪霍翔饶永南陈校非卢晓春
王森,王雪,霍翔,饶永南,陈校非,卢晓春,4
北斗系统QMBOC信号无模糊多径抑制算法研究
王森1,2,3,王雪1,2,3,霍翔1,2,3,饶永南1,2,陈校非1,2,3,卢晓春1,2,4
(1. 中国科学院 国家授时中心,西安 710600;2. 中国科学院 精密导航定位与定时技术重点实验室,西安 710600; 3. 中国科学院大学 电子电气与通信工程学院,北京 101408;4. 中国科学院大学 天文与空间学院,北京 101408)
北斗全球卫星导航系统B1C信号采用正交复用二进制偏移载波(QMBOC)调制,具有更高的跟踪精度。但在非理想信道传输过程中,QMBOC信号多峰特性存在跟踪模糊的问题,同时,多径效应引起的信号畸变会影响定位精度。基于QMBOC信号研究了Bump-Jump、双重估计(DET)跟踪算法,基于窄相关器、高分辨率相关器(HRC)机理推导了多径误差表达式,提出了HRC与DET组合的无模糊多径抑制算法,对比分析了不同组合算法在多径干扰下的跟踪精度,仿真了不同多径误差表达式参数变化下的多径误差包络。研究结果表明,HRC鉴相器与DET组合方法比窄相关技术抗多径能力改善了39%,DET与HRC组合方法对QMBOC信号跟踪稳定性最优,实现了QMBOC信号无模糊多径抑制跟踪。
BDS正交复用二进制偏移载波(QMBOC)信号;Bump-Jump;双重估计(DET);窄相关技术;高分辨率相关器(HRC);无模糊跟踪;多径抑制
0 引言
卫星导航信号体制决定导航系统先天性能,是系统设计和升级过程中考虑的重要因素[1]。随着卫星导航系统的需求和应用逐渐扩展,在同一频点播发多路导航信号是信号体制发展的重要趋势。现代化卫星导航系统广泛地采用了二进制偏移载波(binary offset carrier,BOC)调制和混合二进制偏移载波(multiplexed binary offset carrier,MBOC)调制,具备更强的跟踪精度和抗干扰性能[2-3]。然而BOC、MBOC信号自相关函数的多峰特性,容易导致跟踪环路发生误锁现象,影响导航信号的测距性能。其次,多径效应对信号产生的误差难以通过差分等技术消除,也会导致导航信号的测距性能恶化[4]。
针对BOC信号自相关函数多峰特性造成的误锁现象,P. Fine等人研究了跟踪BOC信号的Bump-Jump技术,但在低载噪比(carrier to noise ratio,C/N0)、多路径等情况下跟踪稳定性不足[5-6]。双重估计(dual estimate technology,DET)跟踪算法通过增加独立的子载波锁定环(sub-carrier locked loop,SLL),对二维相关函数进行锁定,解决了BOC信号跟踪模糊的问题,提高了跟踪稳定性[7-8],但DET算法没有考虑接收信号受多径效应的影响,当接收信号中包含多径信号时,可能会影响DET算法的跟踪效果。针对多径效应影响导航信号测距性能现象,国内外对多径抑制技术展开了研究工作,抑制多径干扰的方法一般可分为两类。第一类是改进天线技术,包括采用双极化天线代替单极化天线抑制多径反射信号的影响[9],以及采用天线阵列技术减轻多径效应的影响[10],但天线技术的改进在一定程度上增加了硬件设计的复杂度和成本。第二类是优化信号接收相关算法,包括改进相关器、多径参数估计以及对观测量后处理。文献[11]提出改进的窄相关技术,采用动态窄相关器跟踪接收信号,降低多径效应造成的测距误差,但受限于相关器的数目以及相关间距的宽度,多径抑制性能不足。文献[12]提出Strobe鉴相器,采用窄相关与宽相关结合的方式抑制多径干扰,具有更强的抗多径性能,但此方法不能直接适用于具有多峰特性的BOC信号。文献[13]基于粒子滤波算法估计多径参数,利用每个粒子信息加权计算多径参数,多径估计参数的准确性对多径干扰下的定位精度有重大影响。文献[14]采用码相关参考波形(code correlation reference waveform,CCRW)技术和优化的Bump-Jump技术确保BOC信号的抗多径性能,但改变CCRW不能普遍适用于导航信号的接收。文献[15]基于频域滤波器采用短时傅里叶变化(short time Fourier transformation,STFT)计算频谱,提取峰值频率,通过插值和逆傅里叶变换,有效消除功率谱峰值的影响,降低多径效应对测距性能的影响,但此方法提高了计算复杂度。基于解决BOC信号多峰特性造成误锁现象以及抑制多径干扰的研究,在不改变天线设计和减小计算复杂度的情况下,本文提出了一种针对QMBOC(quadrature multiplexed BOC)信号的无模糊多径抑制算法,采用DET跟踪算法实现QMBOC信号的无模糊跟踪,并在跟踪环路中采用高分辨率相关器(high resolution correlator,HRC)提高抗多径性能,实现了QMBOC信号无模糊多径抑制跟踪。
本文以BDS(BeiDou Navigation Satellite System)全球系统B1频点正交复用BOC信号作为研究对象,研究了Bump-Jump、DET跟踪算法与窄相关器、HRC机理及多径误差表达式,对Bump-Jump、DET跟踪算法与窄相关器、HRC开展组合算法研究,对比分析了不同组合算法在多径干扰下的跟踪精度,实现了QMBOC信号无模糊多径抑制跟踪。
1 信号调制

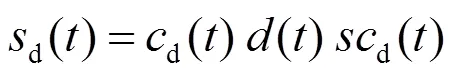

图1为自相关函数和功率谱密度。如图1所示,与BPSK信号相比,BOC和QMBOC信号自相关函数主峰较窄,且功率谱密度具有更多的高频分量,说明BOC和QMBOC信号码跟踪精度更高、多径抑制能力更强[7]。传统跟踪环路对接收的B1C信号跟踪处理时,BOC和QMBOC信号自相关函数多峰特性给信号跟踪带来困难,同时使针对BPSK信号研究的多径抑制技术应用到BOC和QMBOC信号时性能下降。

图1 自相关函数和功率谱密度
2 多径建模及误差分析
本节对多径信号建模,推导不同鉴相器的多径误差近似表达式,定量分析多径效应造成的误差。
2.1 多径信号模型
多径信号可由信号经反射和散射后形成,其中散射信号产生的测距误差很小,在多径误差分析中一般考虑反射信号的影响[18],多径信号表达式为
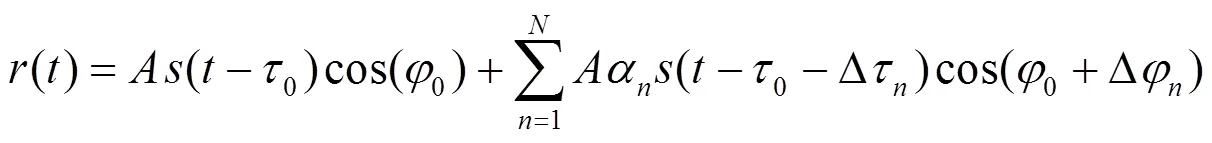
图2是多径效应造成BOC(1,1)信号自相关函数畸变。如图2所示,多径效应对导航信号产生的多径误差使得接收信号与本地参考信号的相关函数发生畸变,影响信号的准确跟踪。

图2 多径效应造成BOC(1,1)信号自相关函数畸变
2.2 多径误差分析
多径效应引起的测距误差指在多径干扰下鉴相器输出零值点与真实零值点之间的差值。在单反射路径信号下,忽略多径环境下信号载波相位误差,非相干超前减滞后(early minus late,EML)鉴相器输出表示为
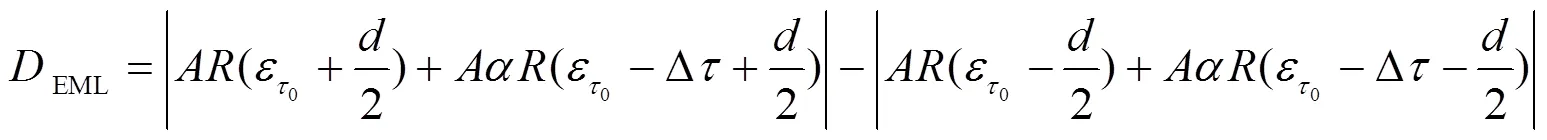
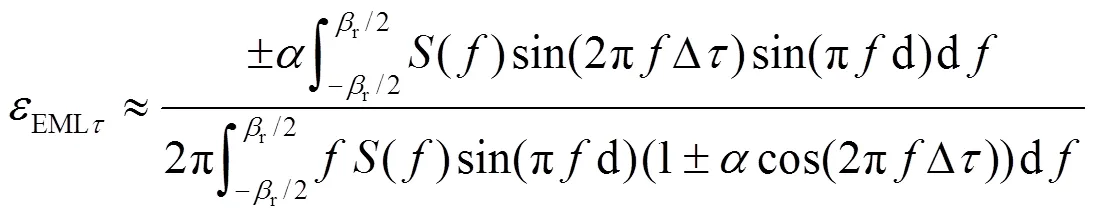

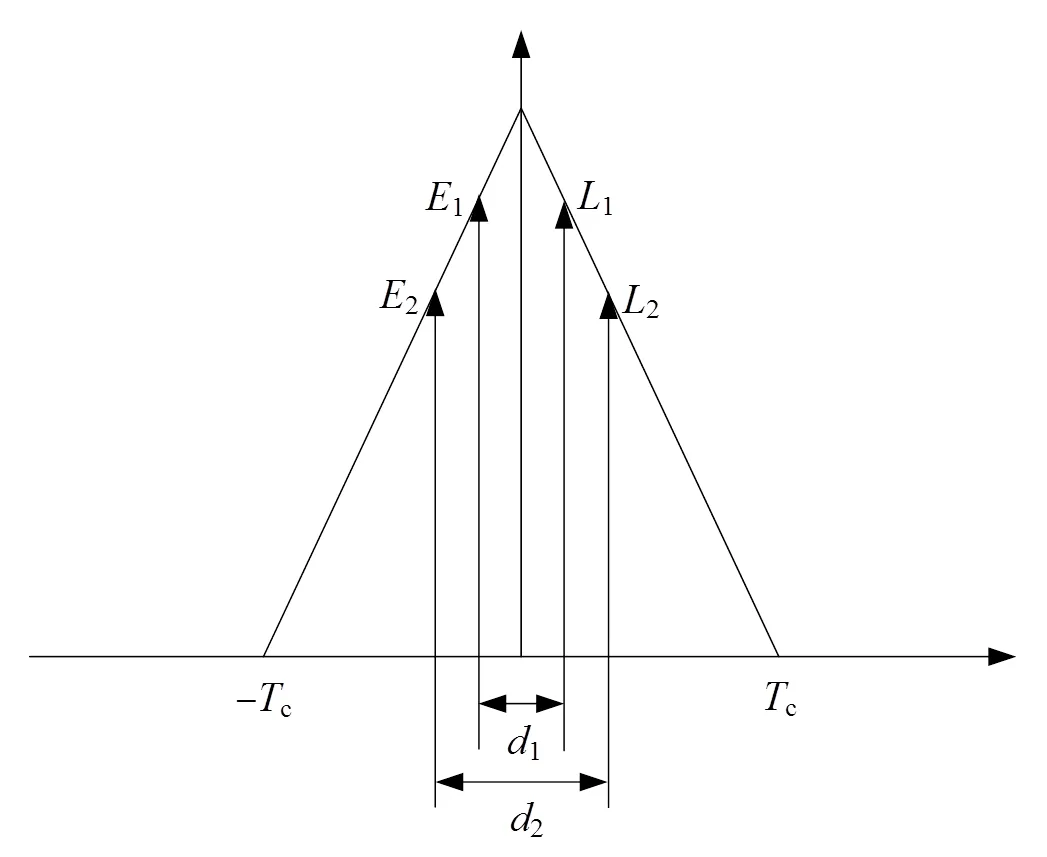
图3 HRC鉴相器配置示意图
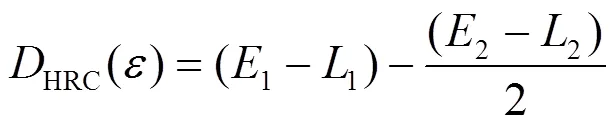
忽略带限信号对鉴相器输出产生的非线性误差,在鉴相器输出零值点附近一阶泰勒展开,HRC输出多径误差近似表达式为
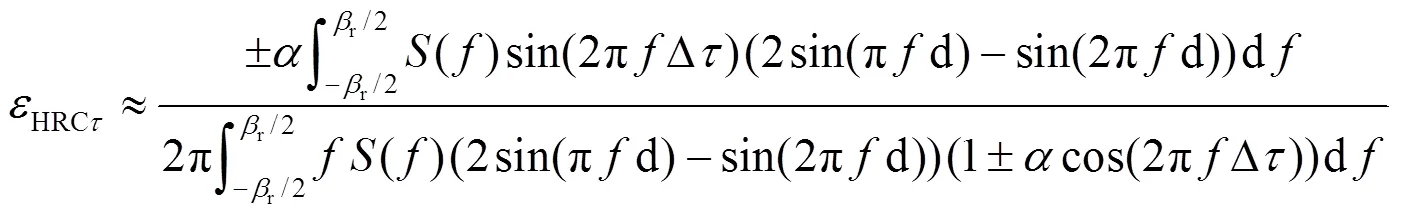
多径误差包络体现码跟踪环路中鉴相器对多径信号的敏感程度,误差包络面积越小,抗多径性能越好[20]。多径误差包络面积表达式为
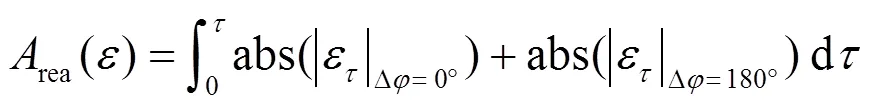
平均多径误差由多径误差包络绝对值累积得到,同样反映了多径抑制性能,其表达式为
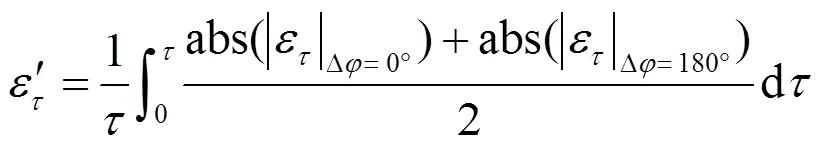
3 QMBOC信号跟踪算法
为解决QMBOC信号跟踪模糊的问题且提高多径抑制性能,提出了HRC与DET组合的无模糊多径抑制算法。
3.1 Bump-Jump
BOC信号自相关函数的多峰特性,容易导致信号在跟踪过程中发生误锁现象。Bump-Jump技术是一种利用旁峰检测是否正确锁定主峰的模糊性跟踪算法,如图4所示,在传统跟踪环路基础上,Bump-Jump技术增加了超超前(very early,VE)和超滞后(very late,VL)两路相关器检测是否发生误锁现象。超前(early,E)、滞后(late,L)支路输出作为主鉴别器输入跟踪码相位,当E、L支路输出相等时,根据VE、VL两路相关器输出,判断是否正确锁定主峰。
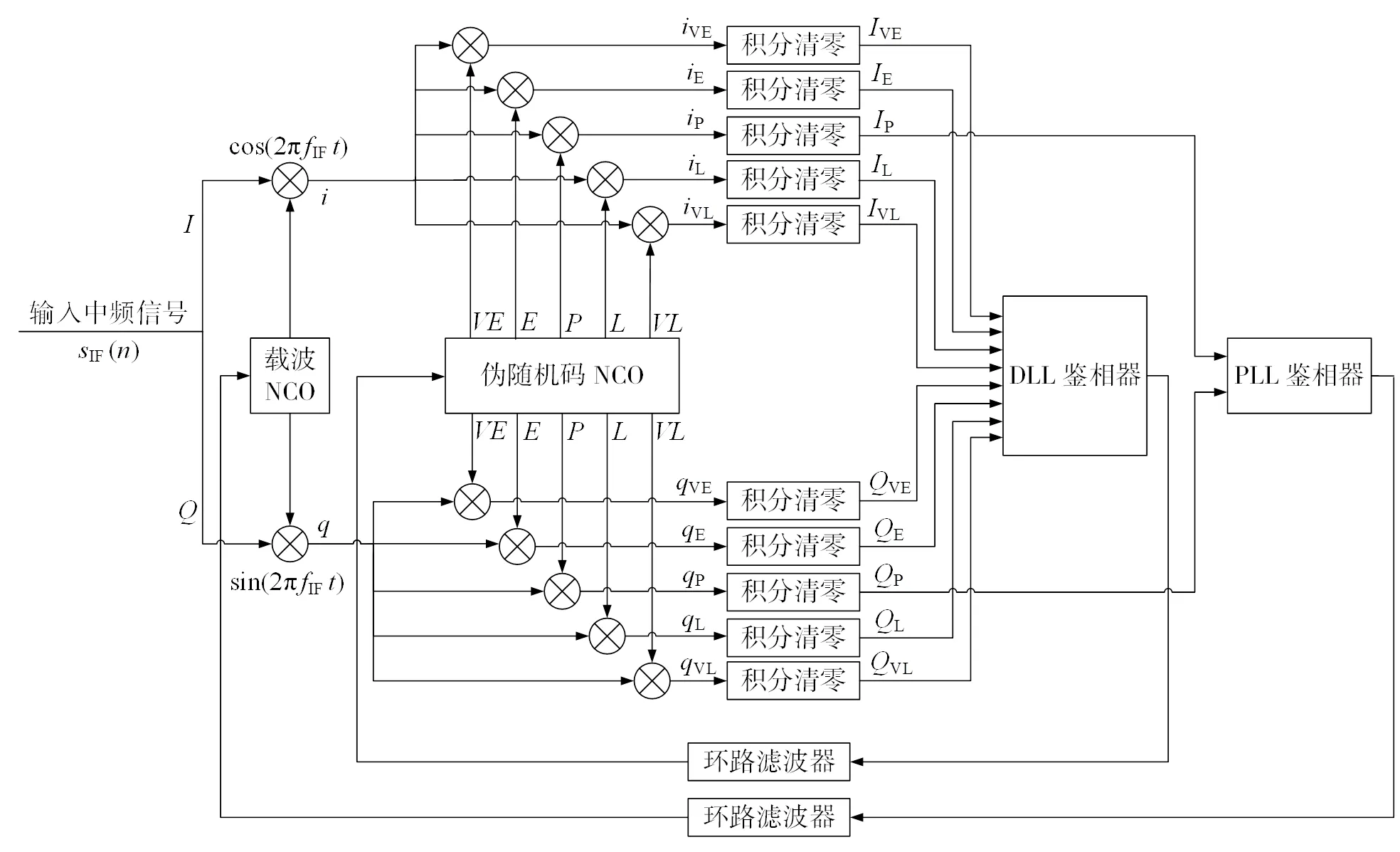
图4 Bump-Jump跟踪环路
在Bump-Jump跟踪环路基础上,为减轻多径效应影响,利用HRC来跟踪接收信号。将式(6)应用到Bump-Jump码跟踪鉴相器中,鉴相器表达式为
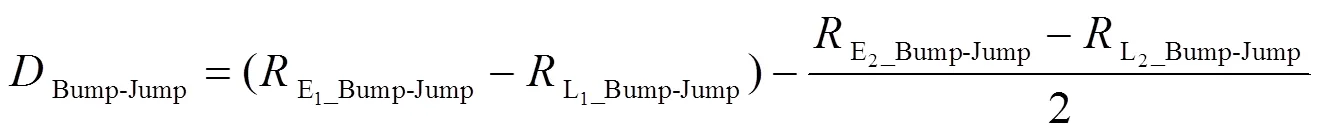

3.2 DET跟踪算法
DET算法是利用多个相关器输出检测信号是否正确锁定的无模糊跟踪算法,适用于各种调制阶数的BOC信号。DET算法将测距码与子载波看作两个独立的变量,增加了SLL结构。接收信号与本地伪随机噪声(pseudo random noise,PRN)码、本地复现子载波做相关运算,得到二维相关函数,其表达式为

图5为二维相关函数。如图5(b)所示,二维相关函数在测距码维度是无模糊的,码周期内仅一个相关峰,相关峰宽度较宽,测距码相位延迟估计值精度较低;如图5(c)所示,子载波维度是周期性且有模糊的,子载波相位延迟估计值等于实际的子载波相位与子载波周期数的和,码周期内有多个相关峰,相关峰宽度较窄,子载波相位延迟估计值精度较高。DET算法锁定二维相关函数时,组合SLL高精度的相位延迟估计值与延迟锁定环路(delay locked loop,DLL)无模糊的相位延迟估计值修正信号相位延迟估计值,得到与SLL精度一致、无模糊的修正信号相位延迟估计值(如式(12)所示),解决了跟踪模糊的问题,跟踪环路结构如图6所示。
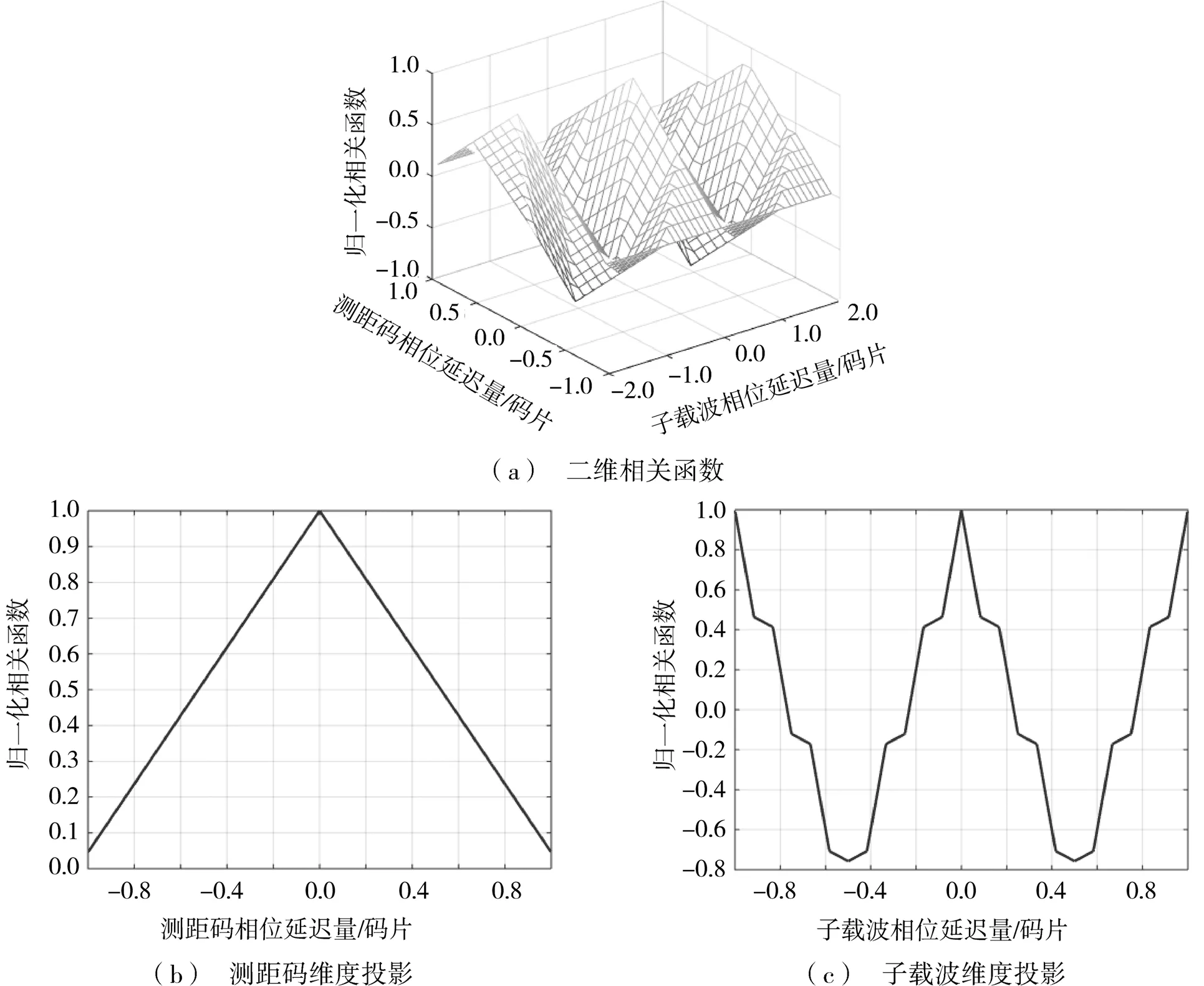
图5 二维相关函数
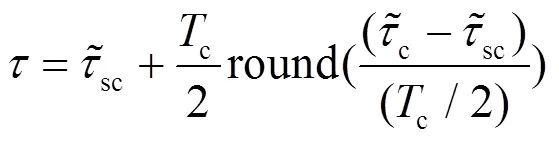
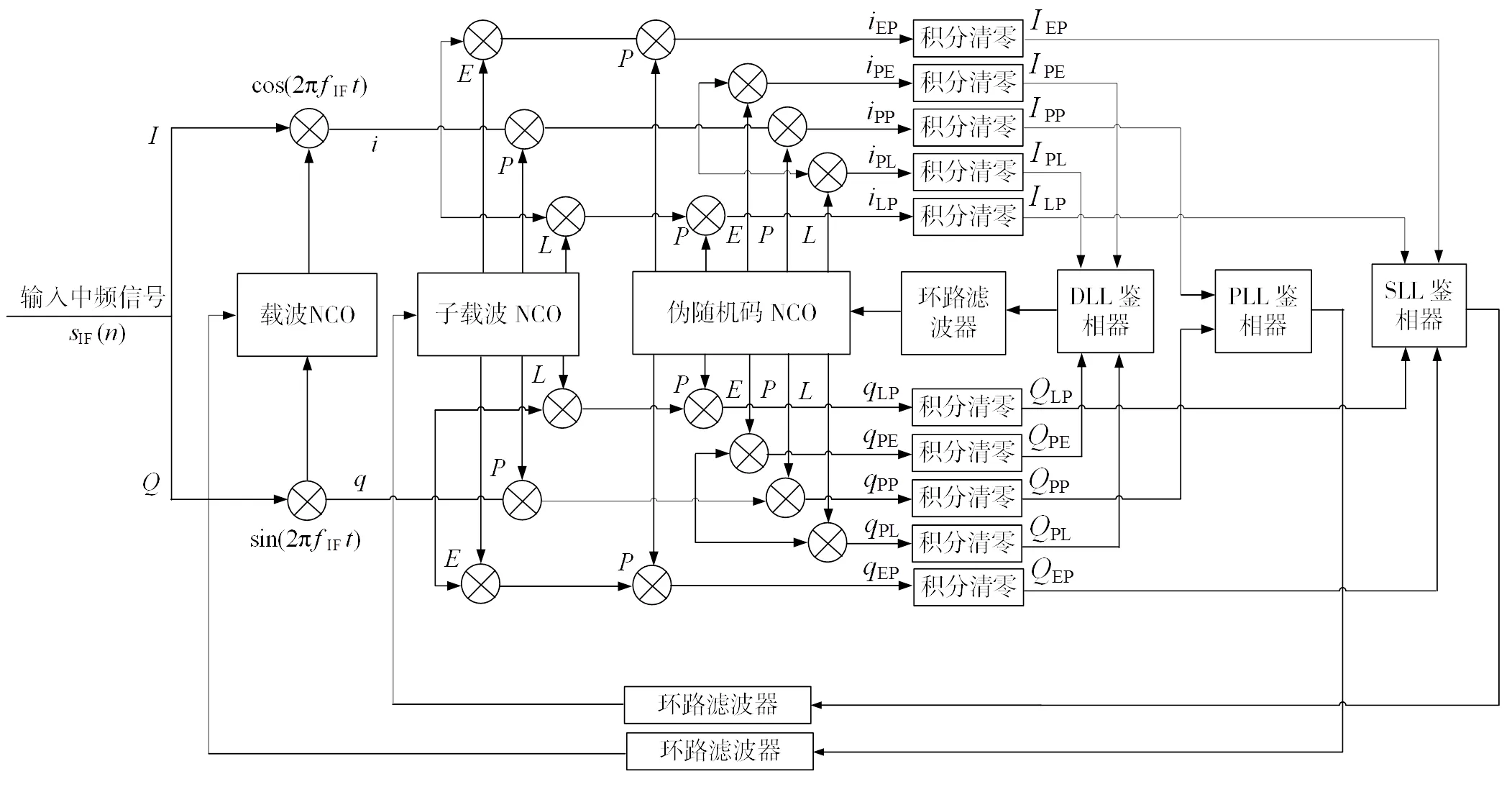
图6 DET跟踪环路
如图6所示,DET算法中的SLL结构与DLL结构一致,存在E,P和L 3路子载波相关输出
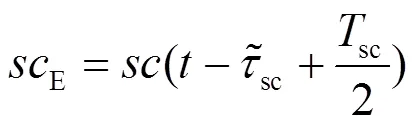

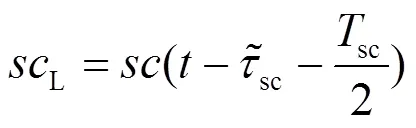
DET算法同相支路相关器输出表达式为

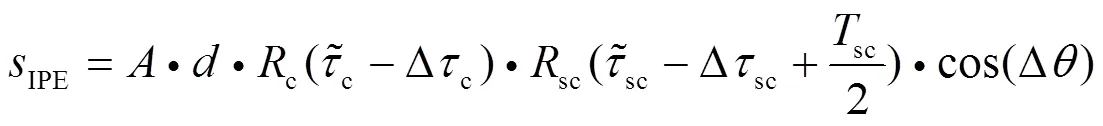
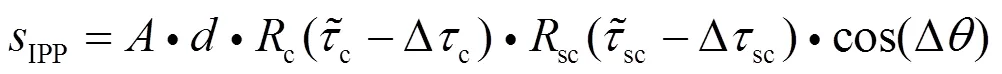
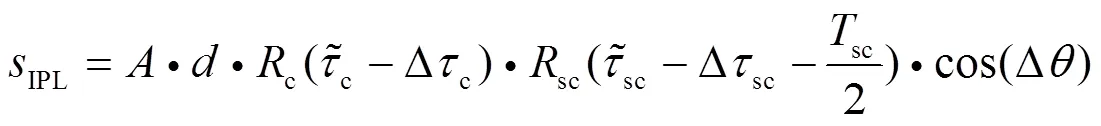
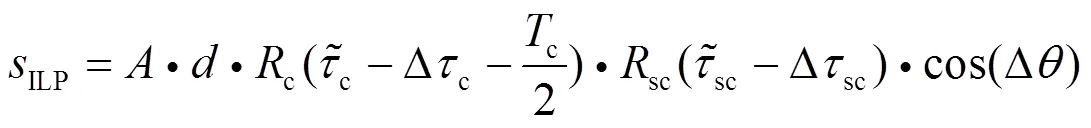
3.3 HRC与DET组合算法
为实现QMBOC信号的无模糊多径抑制跟踪,组合HRC与DET跟踪算法。将式(6)分别应用到DET的DLL、SLL结构中,鉴相器表达式分别为:
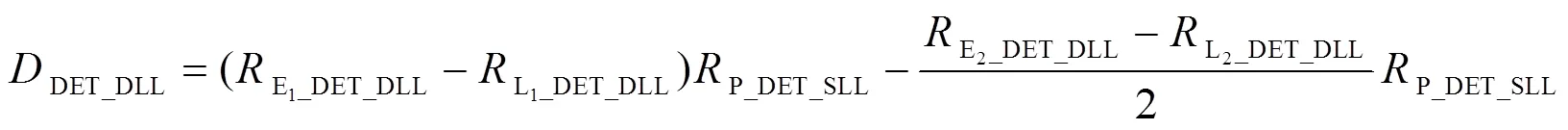
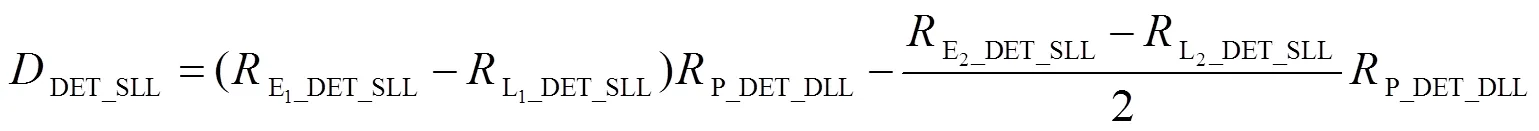
图7为QMBOC信号PRN码EML和HRC鉴相曲线。如图7所示,在(-0.5,0.5)延迟码相位范围内,HRC鉴相器与EML鉴相器对比,相同多径干扰条件下,鉴相器输出结果较小,并在(-0.1,0.1)延迟码相位范围以外输出为零。
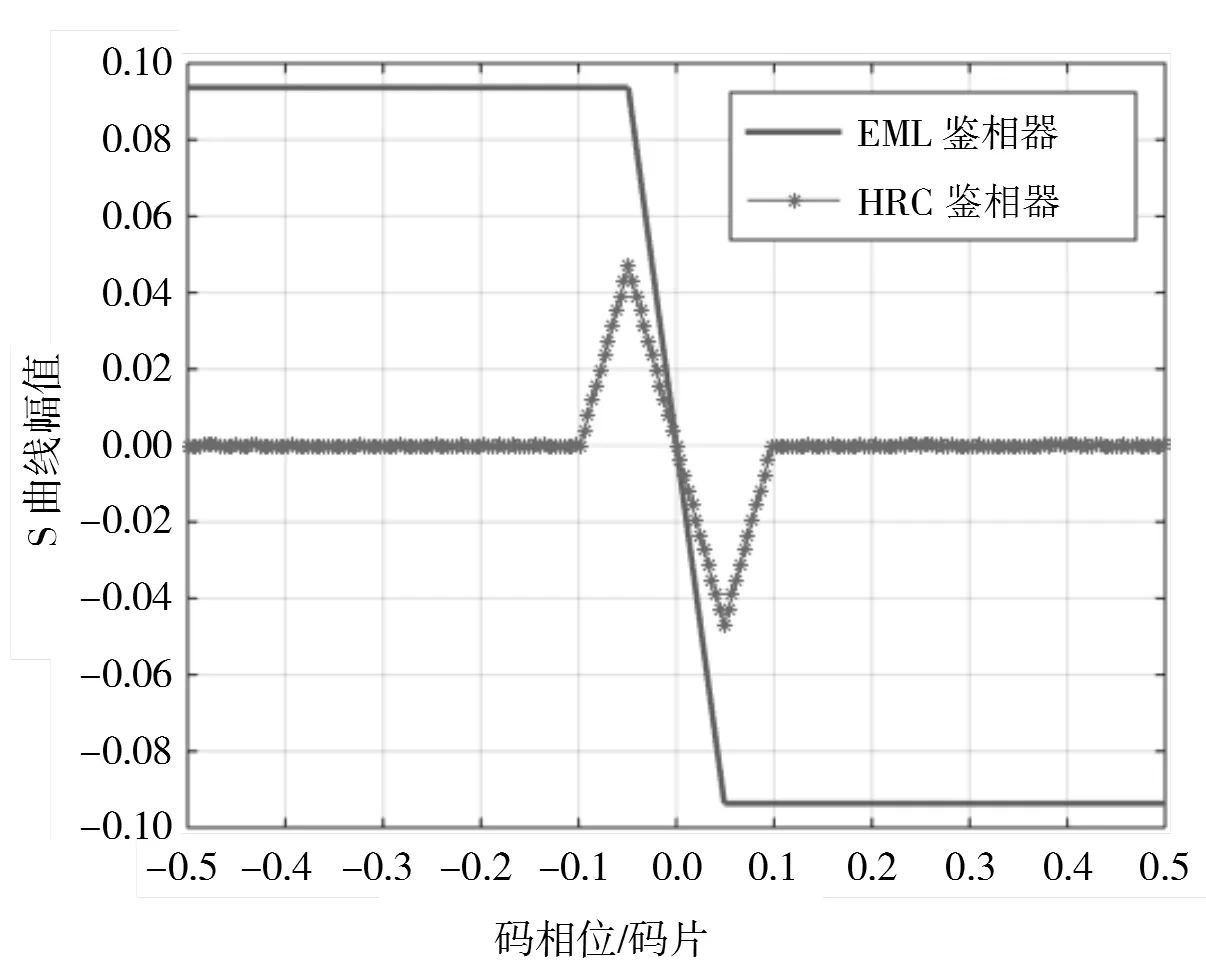
图7 QMBOC信号PRN码EML和HRC鉴相曲线
图8为QMBOC信号子载波EML和HRC鉴相曲线。如图8所示,HRC鉴相器与EML鉴相器对比,相同多径干扰条件下,在(-0.1,0.1)延迟码相位范围内鉴相器输出幅值范围较小。
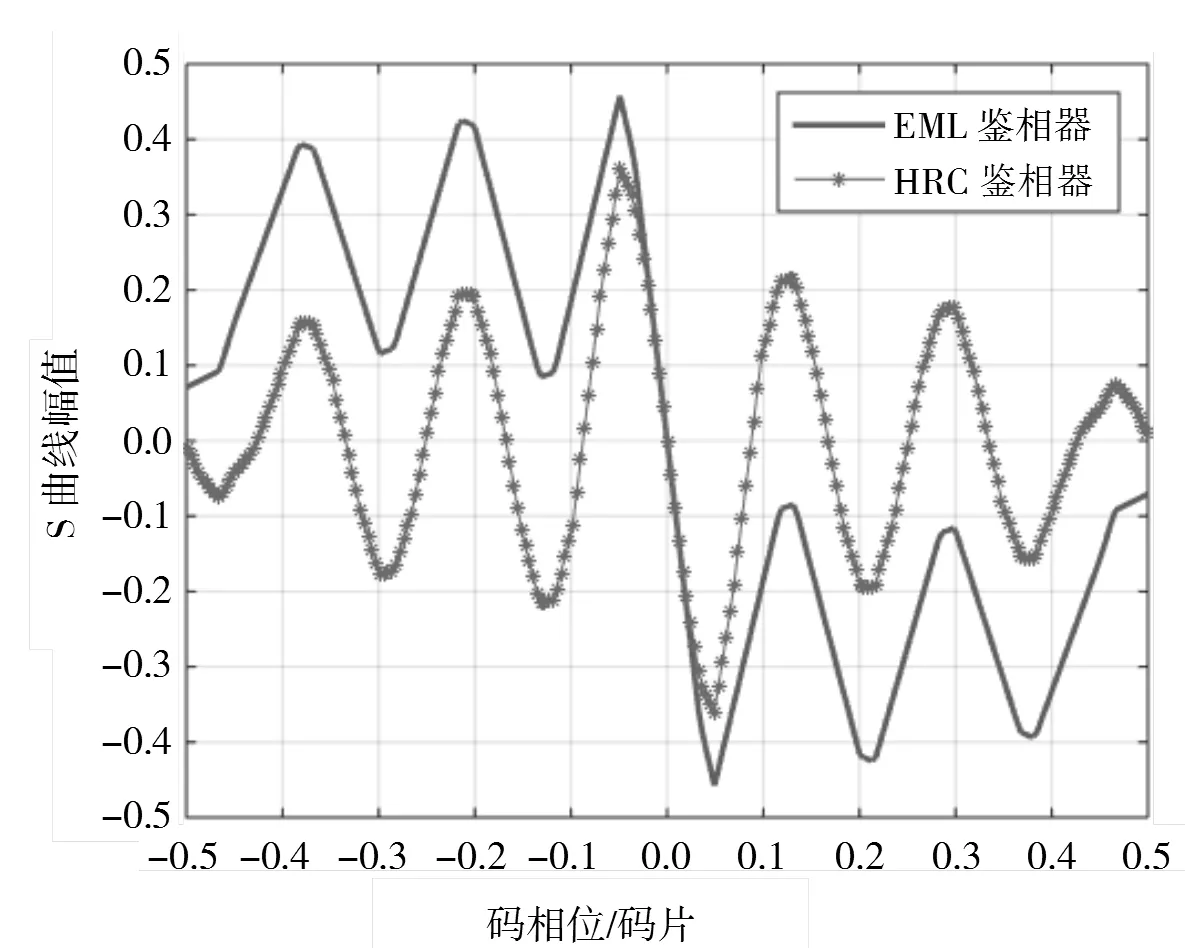
图8 QMBOC信号子载波EML和HRC鉴相曲线
将HRC技术和DET跟踪算法组合应用到DLL、SLL跟踪环路结构中,不仅解决了QMBOC信号跟踪模糊的问题,同时提高了多径抑制性能。
4 仿真分析
根据EML与HRC鉴相器输出多径误差近似表达式,对式(5)和式(7)中引起多径误差变化的MDR、前端带宽、相关间隔、多径延迟长度4个参数进行仿真分析。同时,在多径干扰条件下,对比分析不同组合算法的跟踪精度。
4.1 多径误差仿真分析
仿真不同MDR参数下的多径误差,分别为-3,-6和-10dB,前端带宽为24 MHz,相关间隔分别为0.1和0.01码片,具体仿真条件如表1所示。
表1 不同MDR参数的仿真条件
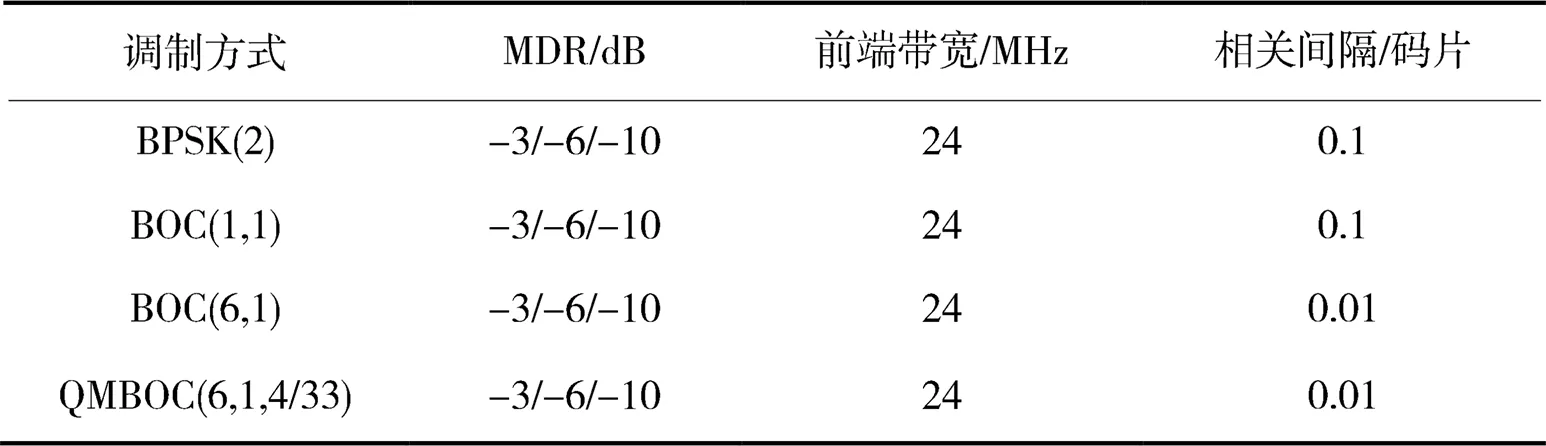
注:MDR为多径信号相对直达信号幅度比。
根据式(5)和式(7),在不同MDR参数下仿真多径误差,多径误差包络如图9所示。

图9 多径误差包络随MDR的变化
对图9所示的多径误差包络绝对值取平均,得到图10所示在不同MDR参数下的平均多径误差。

图10 平均多径误差随MDR的变化
仿真结果表明,不同调制方式的多径误差包络均随MDR变化,MDR越小,多径误差包络面积越小;高阶BOC信号相对BPSK信号有更强的多径抑制能力。相同MDR条件下,HRC比窄相关技术得到的多径误差包络面积更小,多径抑制性能更好,但由于高阶BOC信号具备更强的多径抑制性能,提高精度有限。
仿真不同前端带宽参数下的多径误差,分别为4,10和24 MHz,MDR为-10 dB,相关间隔分别为0.1和0.01码片,具体仿真条件如表2所示。
表2 不同前端带宽参数的仿真条件
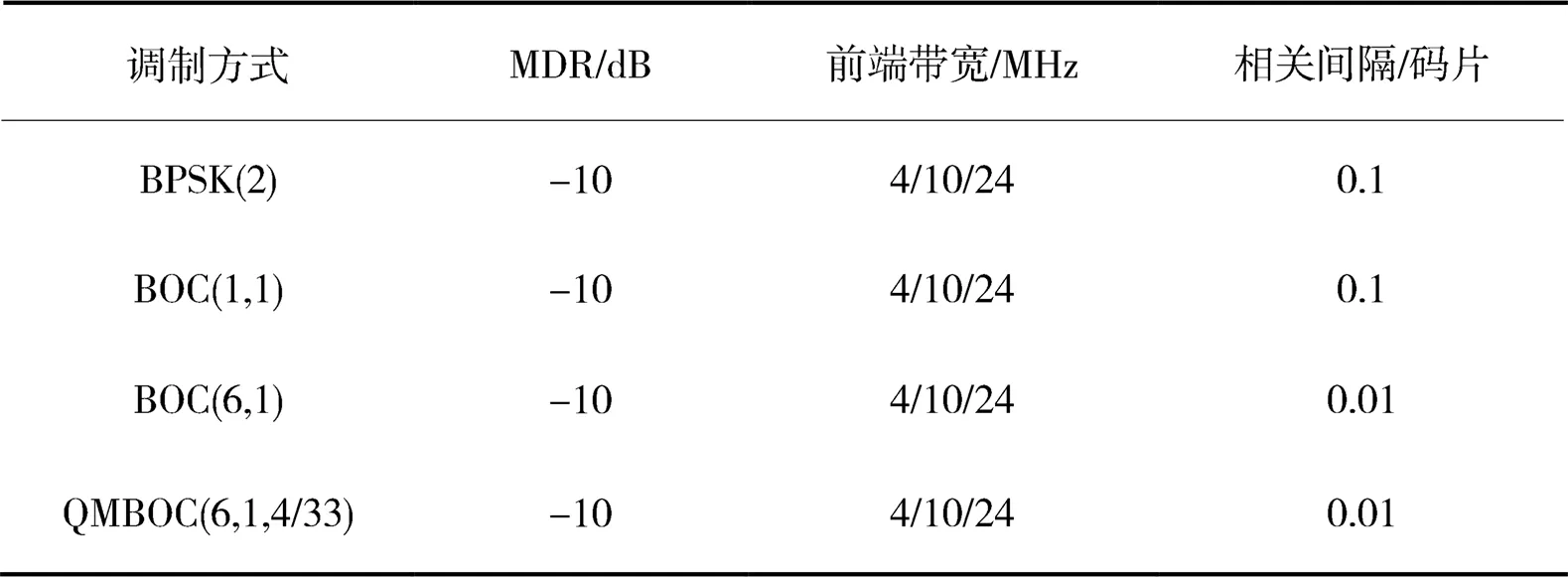
注:MDR为多径信号相对直达信号幅度比。
根据式(5)和式(7),在不同前端带宽参数下仿真多径误差,多径误差包络如图11所示。

图11 多径误差包络随前端带宽的变化
对图11所示的多径误差包络绝对值取平均,得到图12所示在不同前端带宽参数下的平均多径误差。
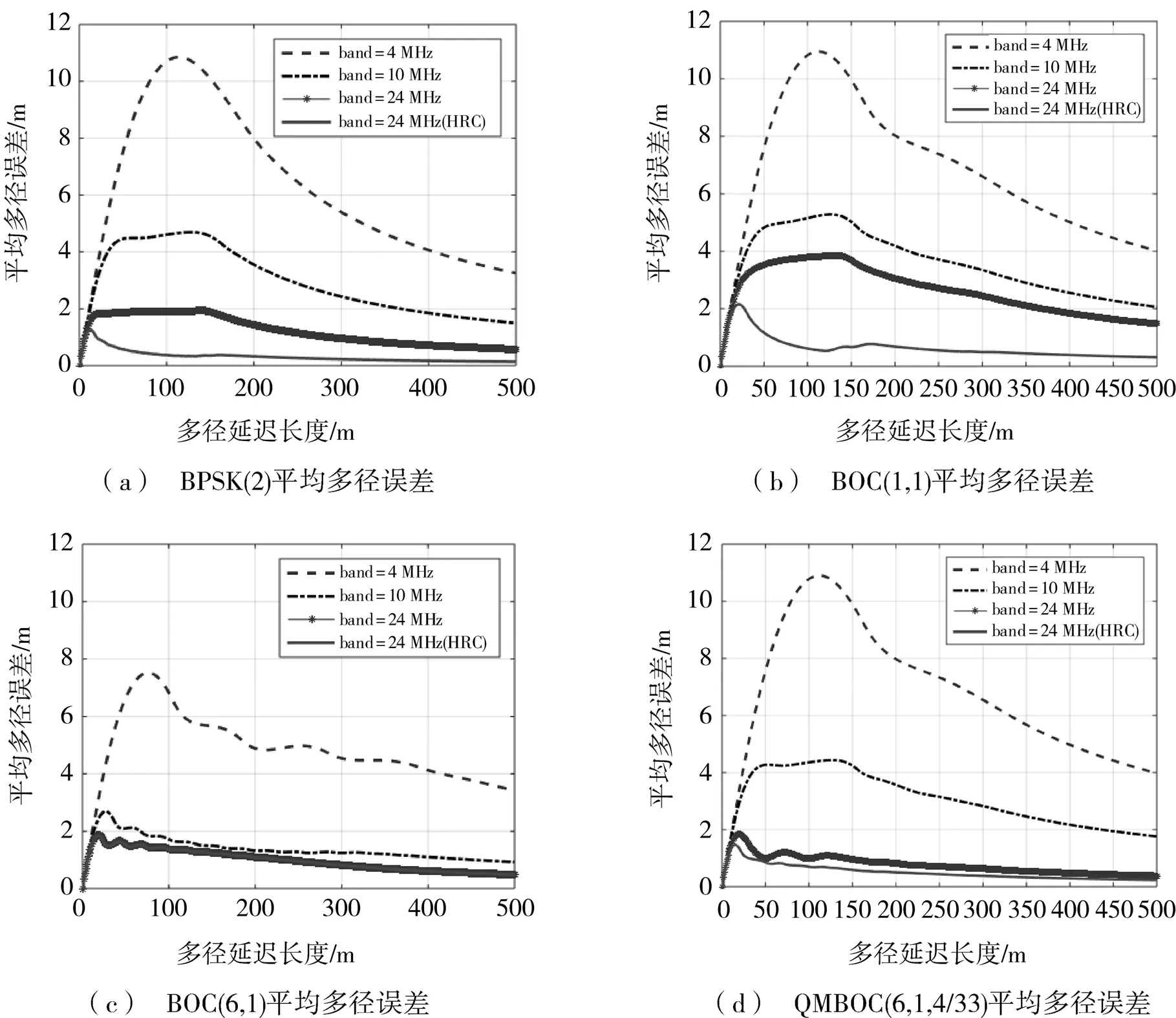
图12 平均多径误差随前端带宽的变化
仿真结果表明,增大前端带宽,不同调制方式下的多径误差包络面积均减小,且高阶BOC信号在同等带宽条件下收敛速度更快,多径误差包络面积更小。相同前端带宽条件下,HRC比窄相关技术得到的多径误差包络面积更小,抗多径性能更好。
仿真不同相关间隔参数下的多径误差,分别为0.01,0.02,0.05和0.07码片,MDR为-6 dB,前端带宽为24 MHz,具体仿真条件如表3所示。
表3 不同相关间隔参数的仿真条件
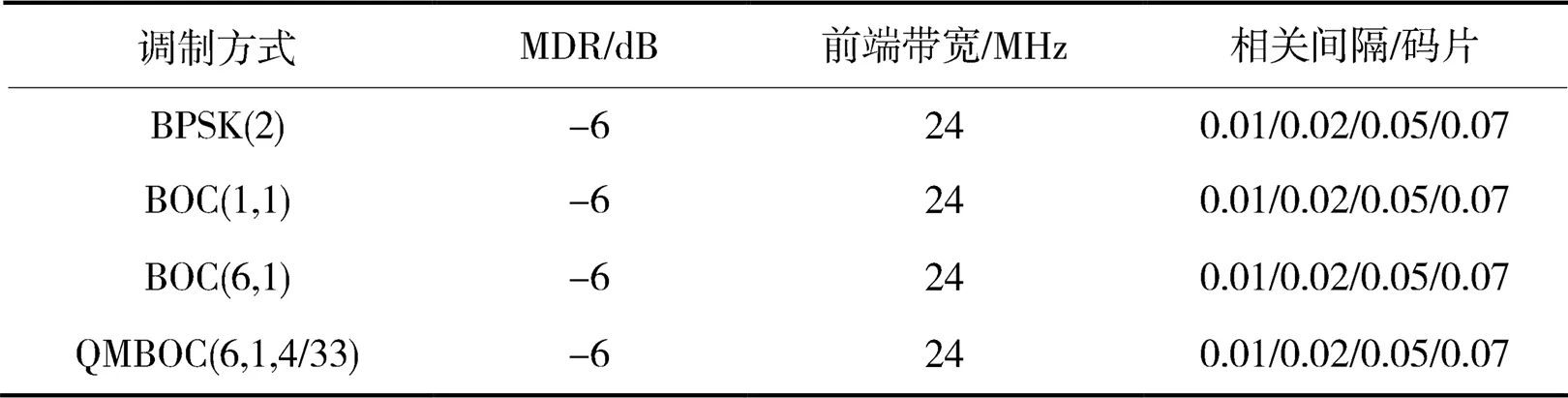
注:MDR为多径信号相对直达信号幅度比。
根据式(5)和式(7),在不同相关间隔参数下仿真多径误差,多径误差包络如图13所示。
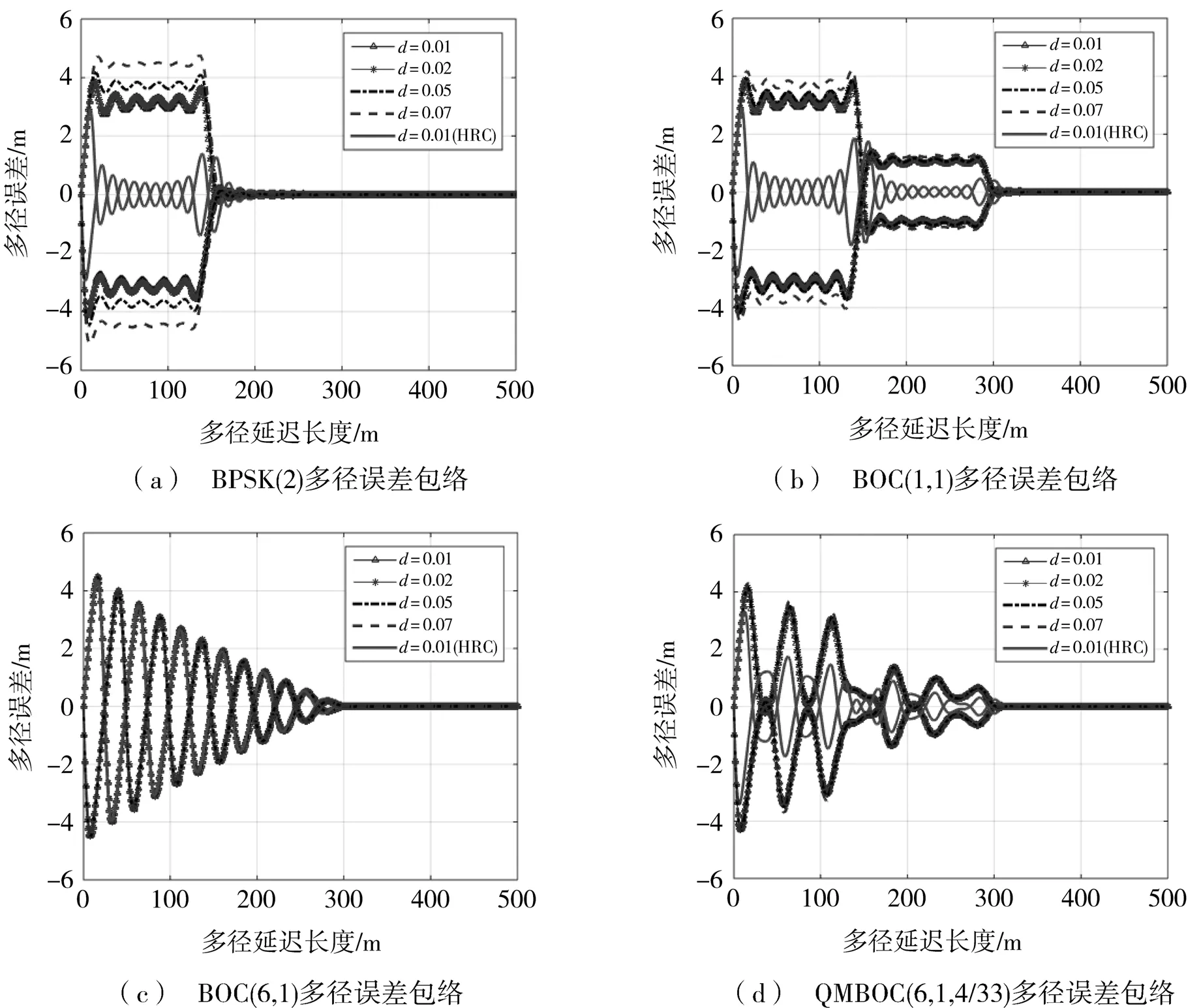
图13 多径误差包络随相关间隔的变化
对图13所示的多径误差包络绝对值取平均,得到图14所示在不同相关间隔参数下的平均多径误差。
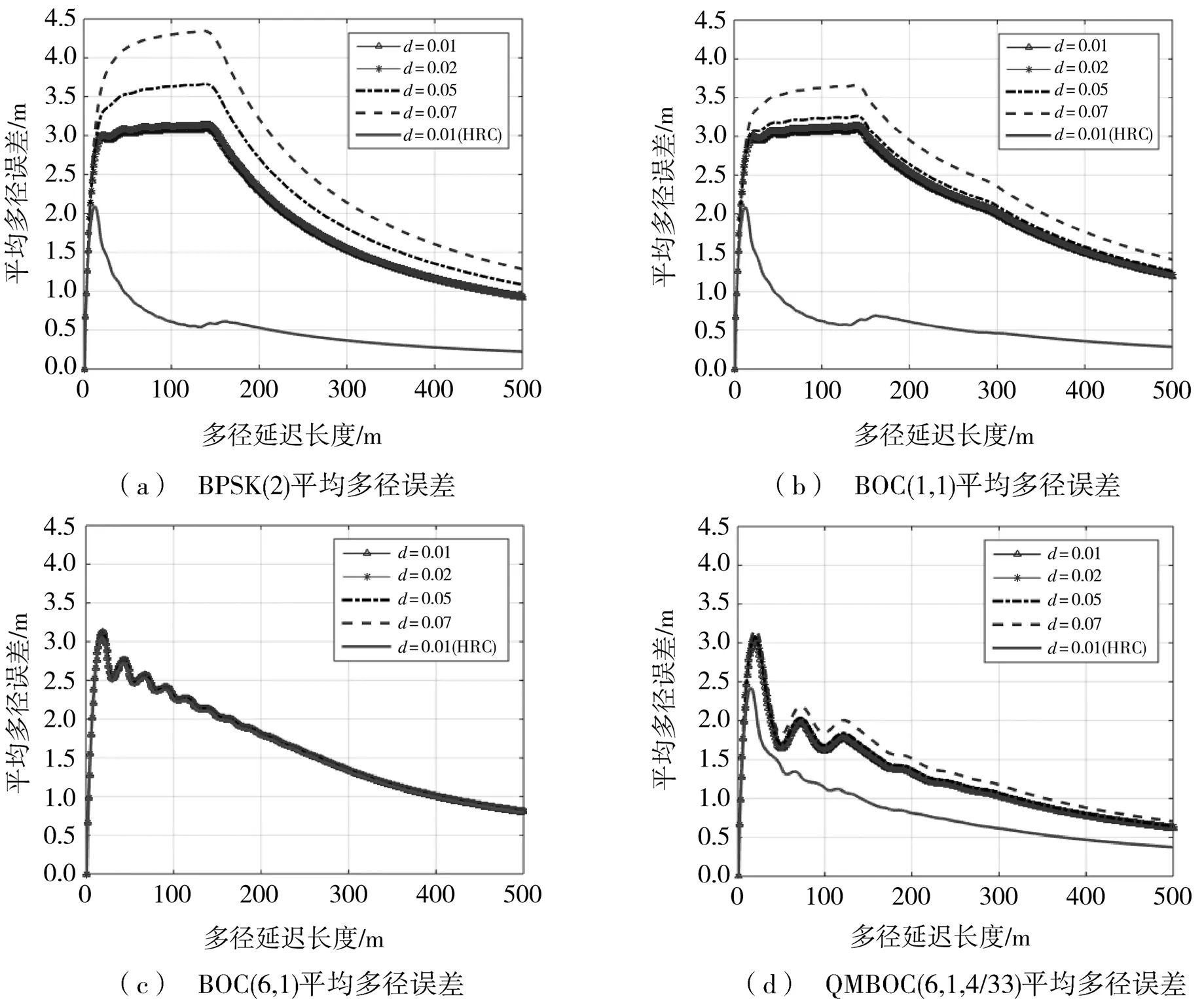
图14 平均多径误差随相关间隔的变化
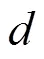
根据表3所示仿真条件,取相关间隔为0.01码片下窄相关与HRC鉴相器的多径误差包络,利用式(8)分别计算窄相关、HRC鉴相器的多径误差包络面积并求其差值,以表明在相同仿真条件下,HRC鉴相器比窄相关器多径误差包络面积的减少程度。将其差值相比于窄相关器多径误差包络面积,以表明HRC鉴相器可在窄相关器基础上对多径误差包络面积的改善程度,分析结果如表4所示。
表4 相关间隔为0.01码片下HRC多径误差包络面积

由上述的仿真结果可知,针对BPSK(2)、BOC(1,1)、QMBOC(6,1,4/33)信号,HRC比窄相关器多径误差包络面积分别改善了86%、76%、39%。
4.2 跟踪算法仿真分析
针对QMBOC信号开展Bump-Jump、DET跟踪算法与HRC、窄相关器组合算法研究,在多径干扰及噪声环境下对比码跟踪精度。仿真C/N0为44 dB·Hz的多径直达信号,MDR为-6 dB。分别在DET与HRC、DET与窄相关器、Bump-Jump与HRC、Bump-Jump与窄相关器组合算法下对不同调制信号进行跟踪验证,鉴相器输出结果如图15所示。
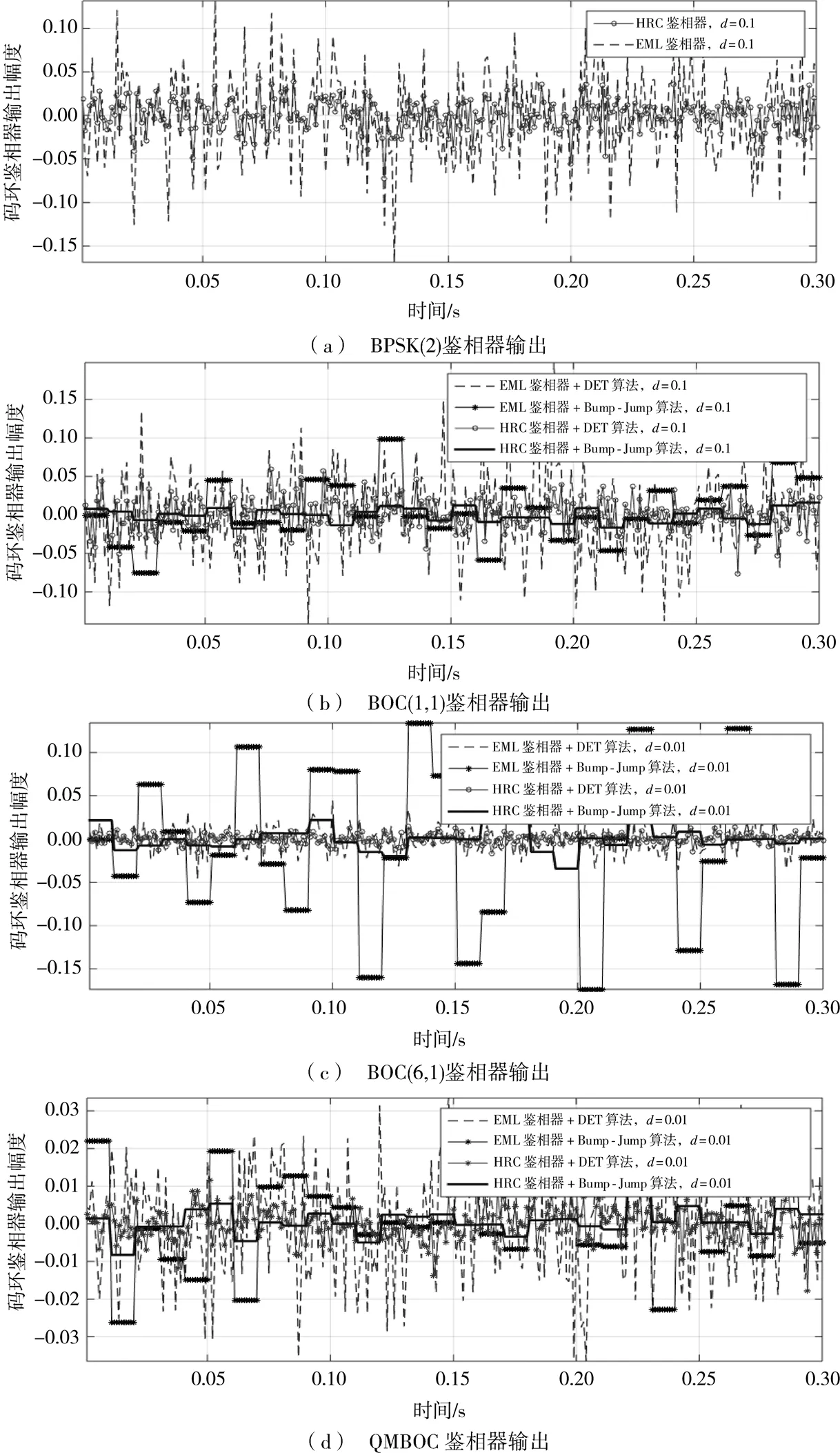
图15 不同组合算法的鉴相器输出
仿真结果表明,由于QMBOC信号中BOC(1,1)分量明显多于BOC(6,1)分量,在匹配跟踪且没有误锁情况下,HRC与DET、Bump-Jump组合的码跟踪精度基本一致,且抗多径性能均优于窄相关技术组合。针对QMBOC信号各分量而言,在没有发生误锁的条件下,基于HRC组合跟踪BOC(1,1)信号的码跟踪精度更高,说明HRC抗多径性能优于窄相关技术;跟踪BOC(6,1)信号时,HRC与DET组合码跟踪精度最高,具有更强的多径抑制性能和解决高阶BOC信号自相关函数多峰特性导致跟踪模糊的能力,跟踪稳定性最优。
综上所述,在多径干扰及噪声环境下,DET与HRC组合跟踪QMBOC信号,有效解决了跟踪模糊问题,同时提高了多径抑制性能,跟踪稳定性最优。
5 结语
本文以QMBOC信号为研究对象,在研究Bump-Jump、DET跟踪算法与窄相关器、HRC鉴相器机理基础上,提出了HRC与DET组合的无模糊多径抑制算法,仿真分析了不同前端带宽、相关间隔、MDR参数变化下的多径误差包络,对比分析了不同组合算法在多径干扰及噪声环境下的码跟踪精度。分析结果表明,不同调制信号下HRC比窄相关器的多径误差包络面积更小,抗多径性能更优;DET跟踪算法实现了QMBOC信号的无模糊跟踪,HRC鉴相器可减轻多径效应对测距性能的影响;在多径干扰及噪声环境下,DET与HRC组合算法,在保证跟踪精度的同时提高了抗多径性能,跟踪稳定性最优。通过以上研究,DET与HRC组合算法用于跟踪QMBOC信号,能够有效解决跟踪模糊问题且提高抗多径干扰性能,可以作为复杂环境下高精度接收机多径抑制设计参考。
[1] 卢晓春, 贺成艳, 王雪, 等. 卫星导航信号评估系统设计及信号性能评估[J]. 时间频率学报, 2016(3): 225-246.
[2] MON A K M, TUN B P T, SHUKLA C M A P. Study and analysis on binary offset carrier(BOC) modulation in satellite navigation systems[J]. IOSR Journal of Electronics and Communication Engineering, 2016, 11(5): 115-123.
[3] HUANG X M, ZHAO X, ZHU X W, et al. MC-BOC: a new interoperable modulation and performance analysis for BeiDou B1 signal[C] // China Satellite Navigation Conference, Singapore: Springer, 2018: 211-220.
[4] KARAIM M, ELSHEIKH M, NOURELDIN A, et al. GNSS Error Sources[M]. Multifunctional Operation and Application of GPS, Intech, 2018: 69-85.
[5] YANG D J, RAO Y N, SHI H H, et al. Quality assessment of Galileo E1A signal[C] // China Satellite Navigation Conference, Singapore: Springer, 2019(1): 410-420.
[6] LI T, TANG Z P, WEI J L, et al. Unambiguous tracking technique based on combined correlation functions for sine BOC signals[J]. The Journal of Navigation, 2019, 72(1): 140-154.
[7] QU B, LI L L, BIAN L, et al. An unambiguous multipath mitigation method based on double-delta correlator for BOC modulation signal[C] // China Satellite Navigation Conference(CSNC) 2016 Proceedings, Singapore: Springer, 2016(1): 571-581.
[8] GAO Y, YAO Z, LU M Q. Theoretical analysis of unambiguous 2-D tracking loop performance for band-limited BOC signals[J]. GPS Solutions, 2018, 22(1): 1-13.
[9] XIE L, CUI X W, ZHAO S H, et al. Mitigating multipath bias using a dual-polarization antenna: theoretical performance, algorithm design, and simulation[J]. Sensors, 2017, 17(2): 359.
[10] VAGLE N, BROUMANDAN A, JAHROMI J A, et al. Performance analysis of GNSS multipath mitigation using antenna arrays[J]. The Journal of Global Positioning Systems, 2016, 14(1): 4-9.
[11] RGHAIF A A, SALMAN S A, ALSHAMARY H A J. Design an adjustable narrow correlator to track GPS signals[J]. Periodical Polytechnical Electrical Engineering and Computer Science, 2019, 63(4): 312-319.
[12] WU J H, DEMPSTER A G. Multipath Mitigation Performance Comparison of Strobe Correlators in GNSS Receivers[C]//Proceedings of International Symposium on GPS/GNSS, Tokyo: [s.n.], 2008: 963-972.
[13] QIN H L, XUE X, YANG Q. GNSS multipath estimation and mitigation based on particle filter[J]. IET Radar, Sonar & Navigation, 2019, 13(9): 1588-1596.
[14] AI P Y, LI C G, GUO X Y, et al. Research on multipath mitigation method for BOC signal based on CCRW technology[C] // 2018 IEEE 4th International Conference on Computer and Communications(ICCC), Chengdu: IEEE, 2018: 1319-1325.
[15] YU S Q, GUO F, ZHANG X H, et al. A new method for GNSS multipath mitigation with an adaptive frequency domain filter[J]. Sensors, 2018, 18(8): 2514.
[16] 中国卫星导航系统管理办公室. 北斗卫星导航系统空间信号接口控制文件公开服务信号B1I[S]. 3.0版. 北京: 中国卫星导航系统管理办公室, 2019.
[17] 中国卫星导航系统管理办公室. 北斗卫星导航系统空间信号接口控制文件公开服务信号B1C[S]. 1.0版. 北京: 中国卫星导航系统管理办公室, 2017.
[18] 唐祖平, 胡修林, 黄旭方. 卫星导航信号设计中的抗多径性能分析[J]. 华中科技大学学报(自然科学版), 2009, 37(5):1-4.
[19] MA C J, TANG X M, LIU Y X, et al. A method of carrier phase multipath based on punctual code correlation reference waveform[C] // China Satellite Navigation Conference, Singapore: Springer, 2018: 477-487.
[20] 刘荟萃, 程肖, 倪少杰, 等. 一种基于误差包络的多径抑制性能评估准则[J]. 国防科技大学学报, 2011, 33(1): 72-75.
Unambiguous multipath mitigation algorithm for BDS quadrature multiplexed binary offset carrier signal
WANG Sen1,2,3, WANG Xue1,2,3, HUO Xiang1,2,3, RAO Yong-nan1,2, CHEN Xiao-fei1,2,3, LU Xiao-chun1,2,4
(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;2. Key Laboratory of Precise, Positioning and Timing Technology, Chinese Academy of Sciences, Xi’an 710600, China;3. School of Electronic and Communication Engineering, University of Chinese Academy of Sciences, Beijing 101408, China;4. School of Astronomy, University of Chinese Academy of Sciences, Beijing 101408, China)
The B1C signal of BeiDou global navigation satellite system used the quadrature multiplexed BOC (QMBOC) modulation, which with higher tracking accuracy. However, in the transmission process of non-ideal channel, the multiple side-peaks caused by QMBOC modulation will cause the ambiguous tracking. In addition, the signal distortion caused by multipath effect will influence the positioning accuracy. This paper studied the tracking algorithms of Bump-Jump and dual estimate technology (DET) based on the QMBOC signal. In addition, the mechanisms of narrow correlator and high resolution correlator (HRC) were also studied, the expressions for multipath error of narrow correlator and HRC discriminator were deduced. Finally, we proposed an unambiguous multipath mitigation algorithm which combined with HRC and DET for QMBOC signal. Based on this algorithm, the tracking accuracy of different combinations was compared and analyzed, and the multipath error envelope with different multipath error expression parameters was simulated. The results show that the multipath mitigation performance based on the combination of DET and HRC discriminator is improved by 39% compared with the narrow correlator technology. What’s more, the combination of DET and HRC has much better tracking stability, and it realizes the unambiguous multipath mitigation tracking for QMBOC signal.
BDS quadrature multiplexedbinary offset carrier (QMBOC) signal; Bump-Jump; dual estimate technology (DET); narrow correlator technology; high resolution correlator (HRC); unambiguous tracking; multipath mitigation
10.13875/j.issn.1674-0637.2020-02-0153-16
2019-11-19;
2020-01-18
中国科学院青年创新促进会人才资助项目
王森,男,硕士,主要从事卫星导航信号基带算法研究。
