星载原子钟频率跳变检测方法仿真分析研究
2020-08-13秦晓伟孙云峰杜二旺王国永
秦晓伟,孙云峰,杜二旺,王国永
星载原子钟频率跳变检测方法仿真分析研究
秦晓伟,孙云峰,杜二旺,王国永
(中国空间技术研究院 西安分院,西安 710000)
卫星导航系统中原子钟的频率跳变直接影响着导航、定位、授时的精度,因此,有必要研究具有实时性、准确性的频率跳变检测方法。首先,通过仿真分析比较基于Kalman滤波器的频率跳变检测方法和基于最小二乘拟合频率跳变检测方法的优缺点,然后结合卫星导航系统中频率跳变检测实时性、准确性的要求,分析、讨论两类检测算法的适用性和可行性。其仿真分析结果表示,单次测量误差信号的差分法可以有效地降低频率跳变检测过程中的误警率,同时提高检测能力;基于Kalman滤波器的频率跳变检测方法能够实时、精确地检测频率跳变,而基于最小二乘拟合的频率跳变检测方法的检测精度很大程度依赖于多项式模型拟合的精度,多项式模型拟合的精度是频率测量值样本数的函数,频率测量值样本越大,多项式拟合模型的精度越高,同时基于最小二乘拟合的频率跳变检测方法的检测能力与判据器的长度有关。因此,基于Kalman滤波器的频率跳变检测方法更适合导航卫星系统中原子钟频率跳变的快速、准确的检测。
频率跳变;卫星导航;Kalman滤波器;最小二乘法
0 引言
在卫星导航系统中,星载原子钟信号的连续性、稳定性直接影响着导航、定位和授时的精度。由于星载原子钟工作环境的变化、空间辐照、老化以及内部的不稳定等因素的影响,导致原子钟输出信号的频率中可能出现异常扰动[1-3]。
由于星载原子钟的频率中存在异常扰动现象,例如频率快变、频率慢变,这些异常扰动直接影响着卫星导航系统的性能以及用户的使用,因此,卫星导航系统中应实时检测星载原子钟的频率跳变,并及时修正频率的异常变化,从而保证用户的正常使用。星载原子钟的频率跳变检测方法应具有实时性和准确性。目前,针对原子钟频率跳变检测的主要方法有块平均法[4]、序列平均法[4]、动态阿伦方差法[5-8]、最小二乘拟合[9]以及基于Kalman滤波器的频率跳变检测的方法[3, 10-14]。块平均和序列平均都是比较常用的方法,但是它们的检测时间比较长,而序列平均方法不能区分频率漂移和频率跳变的现象。动态Allan方差法可以检测任何类型的频率跳变,但不能区分频率跳变的类型,且需要非常大的计算量。
本文针对原子钟频率跳变常用的基于Kalman滤波器的频率跳变检测方法和基于最小二乘拟合检测方法进行仿真分析,从导航卫星对于时钟信号频率跳变检测的实时性和准确性的要求两方面进行算法评估和比较,进而研究两类算法之间的优缺点和两类算法在导航卫星上使用的可行性。
1 原子钟频率跳变检测算法
GNSS系统中常用的原子钟有铷钟、氢钟和铯钟,而这3种原子钟均主要包含3种噪声[3, 15-22]:频率白噪声、频率闪烁噪声和频率随机游走噪声。原子钟噪声模型描述了原子钟独有的特性,文中基于Kalman滤波器建立了GNSS系统中原子钟通用的噪声模型。根据原子钟噪声模型,建立原子钟频率跳变模型,结合原子钟频率变化规律,从而构建原子钟频率跳变检测的模型。
1.1 原子钟噪声模型
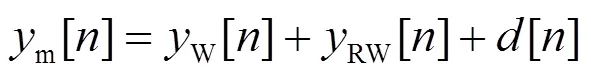
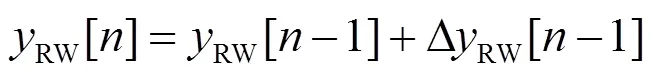

1.2 原子钟频率跳变检测模型
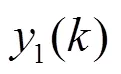
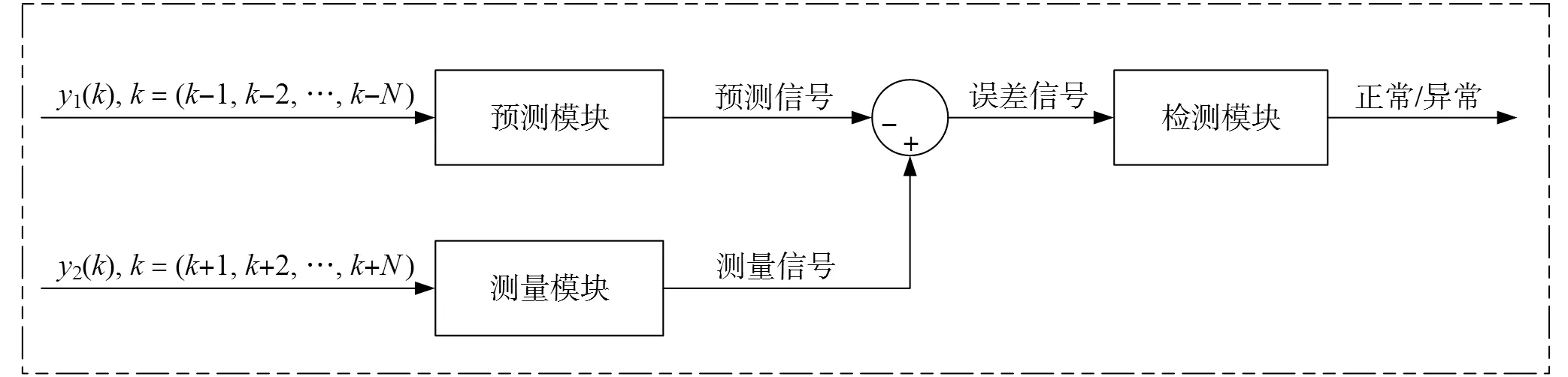
图1 原子钟频率跳变检测模型
图1中预测模块常用的方法有基于Kalman滤波器的频率预测方法[3, 7-9]、基于最小二乘拟合的频率预测方法[6]等。检测模块中常用的判决器有单次测量值法、平均值法、能量累积法、绝对值法[3, 6-9]等。
2 仿真分析与比较
根据GNSS卫星对于原子钟10MHz信号故障检测实时性、准确性的要求,文中主要从故障检测能力、误警率和检测时间3个方面评估故障检测算法优缺点,而故障检测算法选取比较常用的基于Kalman滤波器的频率跳变检测方法和基于最小二乘拟合的频率跳变检测方法。
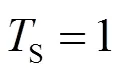
2.1 基于Kalman滤波器的频率跳变检测方法

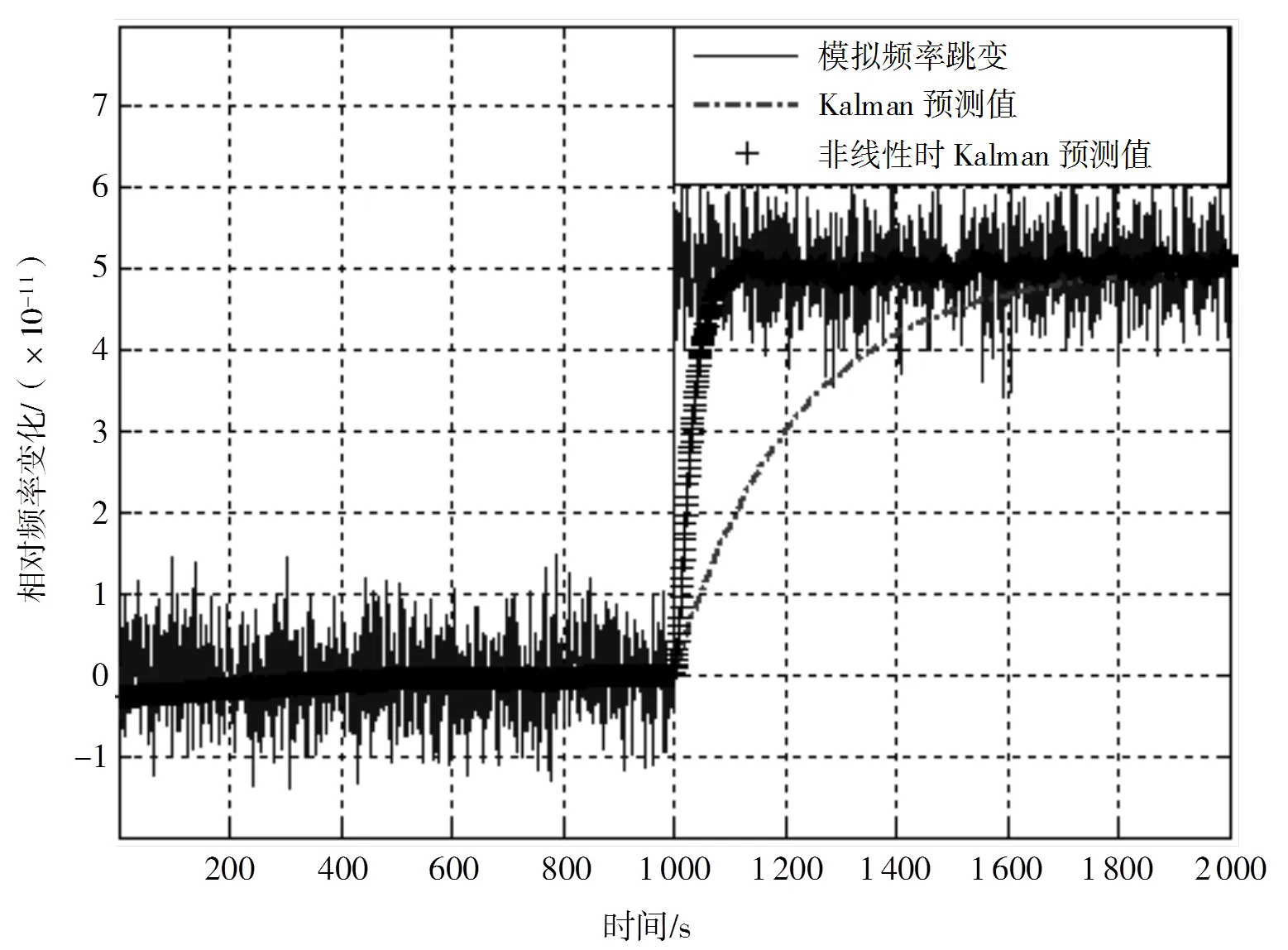
图2 Kalman滤波器预测值

图3 误差信号
图2中Kalman滤波器的响应时间过长,导致图3中误差信号在发生频率跳变处存在比较长恢复时间。由于检测器使用单次测量结果作为频率跳变的判断依据以及Kalman滤波器具有比较长的响应时间,导致该方法具有很高的误警率和比较低的检测能力,如图4(a)所示。
文献[11]在文献[10]的基础上,提出了一种非线性的操作,当原子钟频率存在异常跳变时,通过增大Kalman滤波器的增益,使Kalman滤波器获得更短的响应时间,从而提高检测能力、降低误警率,然而,增加Kalman滤波器的增益导致预测值的噪声增加,如图2中非线性时Kalman预测值。由于Kalman增益是过程噪声和测量噪声的函数,因此仿真过程中Kalman增益的变化是通过调整过程噪声值实现的。表1中给出了2 000次测量过程中,Kalman增益变化与误警次数之间的关系,由表1可知,当原子钟频率发生频率跳变时,适当增加Kalman增益可以有效地降低误警率。图4(b)给出了频率跳变过程中,Kalman增益非线性变化时,阈值参数与误警次数之间的关系。


表1 Kalman增益变化与误警次数之间的关系
当原子钟频率发生频率跳变时,通过增加Kalman增益使得Kalman滤波器具有非常短的响应时间,从而减少误差信号的恢复时间,但是这种非线性的操作导致预测值的噪声增加。


图5 检测信号与滑动窗N长度之间的关系
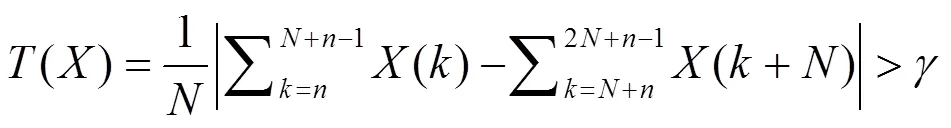
图6中给出了滑动窗长度与检测信号之间的关系,由图可知,滑动窗长度越大,检测信号越大,检测时间越长。图7中给出了原子钟发生频率跳变过程中,Kalman增益变化与检测信号之间的关系,其中Kalman增益的调整是通过值的变化实现的,由图7可知,通过非线性调整Kalman滤波器的增益能够使检测信号变大,提高检测能力,但大大增加了检测时间。由频率跳变检测判据可知,使用长度的滑动窗,则检测时间至少为2×s。
图6 滑动窗长度与检测信号之间的关系
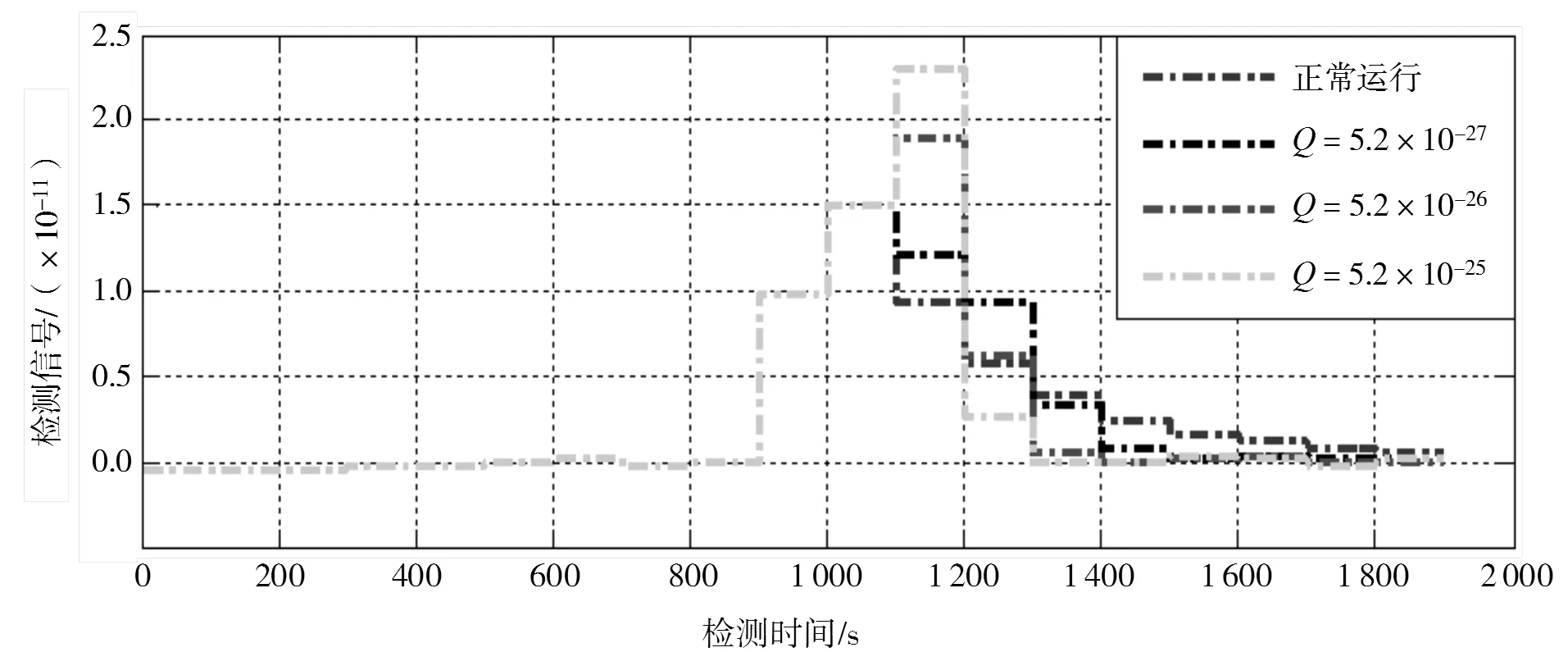
图7 Kalman增益变化与检测信号之间的关系
2.2 基于最小二乘拟合的频率跳变检测方法
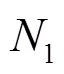

图8 滑动窗的长度与预测值关系
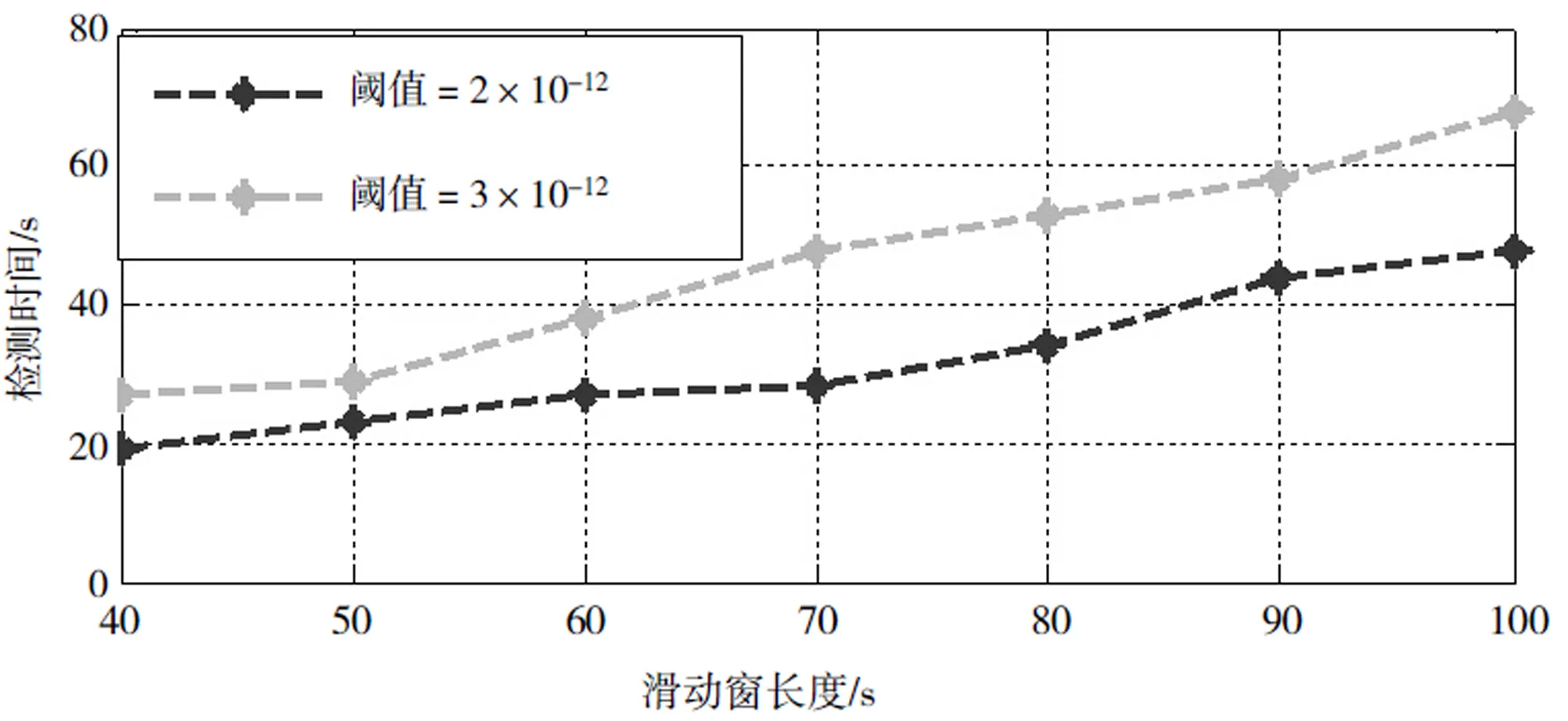
图9 滑动窗长度与检测时间之间的关系
3 结语
通过仿真分析可知,通过对基于Kalman滤波器频率跳变检测方法中单次测量误差信号进行差分,然后利用差分后的误差信号作为检测信号可以有效地降低误警率,提高检测能力。
GNSS卫星要求星载原子钟10 MHz信号的故障检测应具有实时性、准确性,通过对基于Kalman滤波器频率跳变检测方法和基于最小二乘拟合的频率跳变检测方法的仿真分析和比较可知,基于Kalman滤波器的频率跳变检测方法具有实时性,根据采取的频率跳变检测判据不同,检测时间略有不同;而基于最小二乘拟合的频率跳变检测方法需要较长时间的频率测量值拟合二项式模型,且模型需要及时修正。因此,基于Kalman滤波器的频率跳变检测方法更适合GNSS卫星中原子钟10 MHz信号的频率跳变检测。
[1] LEE S W, KIM J, LEE Y J. Protecting signal integrity against atomic clock anomalies on board GNSS satellites[J]. IEEE Transaction on Instrumentation and Measurement, 2011, 60(7): 2738-2745.
[2] KAPLAN E D, HEGARTY C J. Understanding GPS: Principles and Applications[M]. 2nd ed. Boston, Ma: Artech House, 2006.
[3] HUANG X M, GONG H, OU G. Detection of weak frequency jumps for GNSS on board clocks[J]. IEEE Transaction Ultrasonics Ferroelectrics Frequency Control, 2014, 61(5): 747-755.
[4] RILEY W J. Algorithms for frequency jump detection[J]. Metrologia, 2008, 45(6): S154-S161.
[5] GALLEANI L, TAVELLA P. The characterization of clock behavior with the dynamic Allan variance[J]. IEEE International Frequency Control Symposium, 2003: 239-244.
[6] GALLEANI L, TAVELLA P. The dynamic Allan variance[J]. IEEE Transaction Ultrasonics Ferroelectrics Frequency Control, 2009, 56(3): 450-464.
[7] GALLEANI L. The dynamic Allan variance II: A fast computational algorithm[J]. IEEE Transaction Ultrasonics Ferroelectrics Frequency Control, 2010, 57(1): 182-188.
[8] SESIA I, GALLEANI L, TAVELLA P. Application of the dynamic Allan variance for the characterization of space clock behavior[J]. IEEE Transaction Aerospace Electronics System, 2011, 47(2): 884-895.
[9] GALLEANI L, TAVELLA P. Robust detection of fast and slow frequency jumps of atomic clocks[J]. IEEE Transaction Ultrasonics Ferroelectrics Frequency Control, 2017, 64(2): 475-485.
[10] GALLEANI L. Detection of atomic clock frequency jumps with the Kalman filter[J]. IEEE Transaction Ultrasonics Ferroelectrics Frequency Control, 2012, 59(3): 450-464.
[11] MOHAMED E M, SHALASH A F, KAMAL H A. Fast accurate detection of frequency jumps using Kalman filter with non linear improvements[J]. International Journal of Electrical, Computer, Energetic, Electronic and Communication Engineering, 2014, 8(2): 469-473.
[12] KHARE A, ARORA R, ALAK B, et al. Autonomous rubidium clock weak frequency jump detector for onboard navigation satellite system[J]. IEEE Transaction Ultrasonics Ferroelectrics Frequency Control, 2016, 63(2): 326-335.
[13] SONG H J, DONG S W, WU W J. Detecting an atomic clock frequency anomaly using an adaptive Kalman filter algorithm[J]. Metrologia, 2018, 55(3): 350-359.
[14] DAVIS J A, GREENHALL C A, STACEY P W. A Kalman filter clock algorithm for use in the presence of flicker frequency modulation noise[J]. Metrologia, 2005, 42(1): 1-10.
[15] HUANG X M, GONG H, OU G. Detection of weak frequency anomalies for atomic clocks with a Kalman filter[J]. Metrologia, 2014, 51(3): 183-190.
[16] TAVELLA P. Statistical and mathematical tools for atomic clocks[J]. Metrologia, 2008, 45(6): S183-S192.
[17] PANFILO G, TAVELLA P. Atomic clock prediction based on stochastic differential equations[J]. Metrologia, 2008, 45(6): S108-S116.
[18] RILEY W J, HOWE D A. Handbook of frequency stability analysis[K]. 2007.
[19] GALLEANI L, SACERDOTE L, TAVELLA P, et al. The mathematical model for the atomic clock error: an overview[J]. Metrologia, 2003,40(3):257-264.
[20] KAY S M. Fundamentals of Statistical Signal Processing, Volume 2: Detection Theory[M]. New Jersey: Prentice Hall, 1998.
[21] NUNZI E, GALLEANI L, TAVELLA P, et al. Detection of anomalies in the behavior of atomic clocks[J]. IEEE Transaction on Instrumentation and Measurement, 2007, 56(2): 523-528.
[22] GALLEANI L. A tutorial on the two-state model of the atomic clock noise[J]. Metrologia, 2008, 45(6): S175-S182.
The research on simulation analysis of on-board atomic clock frequency jump detection method
QIN Xiao-wei, SUN Yun-feng, DU Er-wang, WANG Guo-yong
(China Academy of Space Technology (Xi’an), Xi’an China, 710000)
The frequency jump of atomic clock in satellite navigation system directly affects the precision of navigation, positioning and timing. Therefore, it is necessary to study the frequency jump detection method with real-time and accuracy. Firstly, the advantages and disadvantages of the frequency jump detection method based on Kalman filter and least squares fitting are compared by simulation analysis. Then, combined with the requirements of real-time and accuracy for frequency jump detection in satellite navigation system, the applicability and feasibility of two types of detection algorithms are analyzed and discussed. The simulation analysis results shown that the difference method for the single measurement error signal can effectively reduce probability of false detection and improve detection capabilities. Frequency jump detection method based on Kalman filter can detect frequency jump in real time and accurately. However, the detection precision of the frequency jump detection method based on least squares fitting depended largely on the precision of the polynomial fitting model as the precision of the polynomial model fitting is a function of the number of samples of the frequency measurement, the larger the frequency measurement sample, the higher precision of the polynomial fitting model. In addition, the detection capability of the frequency jump detection method based on least squares fitting is related to the length of the criterion. Therefore, the frequency jump detection method based on Kalman filter is more suitable for fast and accurate detection of atomic clock frequency jump in navigation satellite systems.
frequency jump; satellite navigation; Kalman filter; least-squares
10.13875/j.issn.1674-0637.2020-02-0113-08
2019-11-25;
2020-01-21
国家自然科学基金青年基金资助项目(11803023);国家自然科学基金国家重大科研仪器研制资助项目(61627817)
秦晓伟,男,工程师,主要从事导航卫星时间基准研究。
