提升超深层超高压气藏动态储量评价可靠性的新方法<br/>——物质平衡实用化分析方法

提升超深层超高压气藏动态储量评价可靠性的新方法
——物质平衡实用化分析方法

2020-08-13孙贺东李原杰燕朱松柏付小涛孟广仁

天然气工业 2020年7期

孙贺东曹雯李君贾伟李原杰吴燕朱松柏付小涛杨敏孟广仁

1. 中国石油勘探开发研究院 2. 中国石油塔里木油田公司

0 引言

随着勘探开发技术的不断进步，中国石油天然气股份有限公司（以下简称中国石油）近年来在四川盆地、塔里木盆地库车山前构造带相继发现并开发了一批超深层大气田（气藏中部埋藏深度超过4 500 m）。其中仅在塔里木盆地探明天然气地质储量就超过1×1012m3，天然气年产量已接近300×108m3。由于超深层大气田一般具有高压超高压、基质致密、裂缝发育等特点，采用动态法计算的储量（以下简称动态储量）具有较强的不确定性，动、静态储量比介于37%～94%[1-2]，压缩系数、气藏采出程度、基质供气能力、裂缝性水侵是影响超深层超高压气田动态储量评价结果准确性的主要因素。压降法是评价气藏动态储量的常用方法[3]，由于压缩系数难以确定，使得气藏动态储量的计算误差大，甚至会超过100%[2,4]；若未达到采用压降法计算动态储量的起算条件（pD—Gp关系曲线偏离直线），误用该方法，亦会造成严重偏差。为此，笔者基于高压超高压气藏物质平衡方程，深入分析了岩石有效压缩系数（Cf）、岩石累积有效压缩系数的相关关系，进而优选出适合于高压超高压气藏动态储量评价的物质平衡分析方法；然后，基于非线性回归法确定了动态储量评价的起算条件，针对未达到起算条件的情形建立了半对数典型曲线拟合法，并在3个超高压气田（藏）进行了应用。可靠的动态储量评价结果将为合理制订高压超高压气藏开发技术对策奠定坚实的基础。

1 高压超高压气藏物质平衡方程

1.1 物质平衡方程的形式

对于封闭型高压超高压气藏，若不考虑水侵量及注气量，物质平衡方程表示为[5]：

式中p表示平均地层压力，MPa；Z表示天然气偏差因子，无量纲；表示气藏累积有效压缩系数，MPa－1；Gp、G分别表示累计产气量和动态储量，108m3；下标i表示原始状态。

式中Swi表示原始含水饱和度；表示地层水累积压缩系数，MPa－1；表示岩石累积有效压缩系数，MPa－1；M表示水体倍数。

若不考虑水体的影响，即M＝0，式（2）简化为：

国内外学者在计算高压超高压气藏动态储量时，习惯于用气藏有效压缩系数（Ce）简单代替即假设开发过程中高压超高压气藏近似不变[6-14]，岩石累积有效压缩系数、地层水累积压缩系数被视为常数。

Ce计算式为：

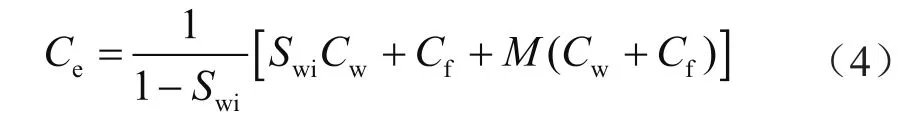
式中Ce表示气藏有效压缩系数，MPa－1；Cw表示地层水压缩系数，MPa－1；Cf表示岩石有效压缩系数，MPa－1。

1.2 不同形式的压缩系数

为了正确应用物质平衡方程计算高压超高压气藏动态储量，首先要弄清的定义及其相互关系。Cf定义为压力每变化1 MPa条件下单位孔隙体积的变化率，即

式中Vp、V分别表示岩石孔隙体积和岩石体积，m3；φ表示孔隙度。

对于常压气藏，若不考虑孔隙度的应力敏感性，通常认为Cf是不随地层压力变化而改变的参数；而对于高压超高压或裂缝性气藏，由于受到孔隙度应力敏感性的影响，其Cf值远高于常规气藏的Cf且随地层压力变化将发生改变。由于受到实验室条件的限制，在室内很难获取Cf在实际地层条件下的变化规律。在应用式（1）计算高压超高压气藏的动态储量时，用Ce代替而Ce由式（4）计算得到，其中Cf的不确定性会造成动态储量计算结果不确定，从而导致开发工作者难以做出正确的决策。例如选取克深2气藏29块全直径岩心，通过覆压测试得到Cf在原始地层条件下介于 5×10－4～ 25×10－4MPa－1[7],相应的动态储量计算结果介于800×108～440×108m3，计算结果最大值与最小值的比值为182%。

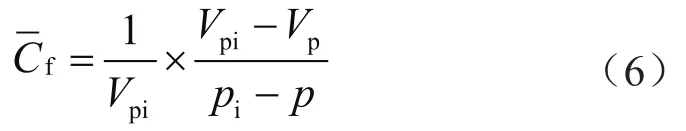
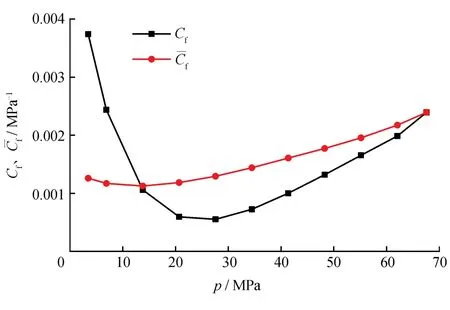
图1 Cf、与p关系曲线图

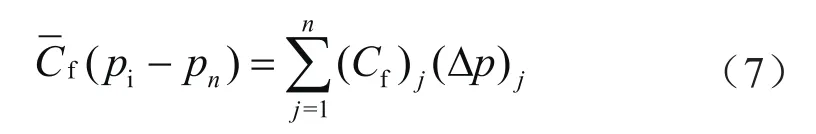
式中下标n、j表示时刻。

综上所述，基于物质平衡方程计算高压超高压气藏动态储量时，不能将Cf与混为一谈，也不能简单地用Ce代替。与采用Ce计算超高压气藏动态储量的结果类似，的取值对动态储量计算结果影响也很大。

2 高压超高压气藏动态储量评价方法

2.1 评价方法优选

物质平衡法是计算动态储量的传统方法，按是否需要压缩系数可以划分为两类（表1）。由于Ce和难以准确计算出，因此不宜采用需要Ce的方法进行动态储量评价；在不需要Ce的方法中，线性回归法对原始地层压力敏感性强，抛物式拟合法对于大型气藏误差大。因此，推荐选用非线性回归法计算此类气藏的动态储量。

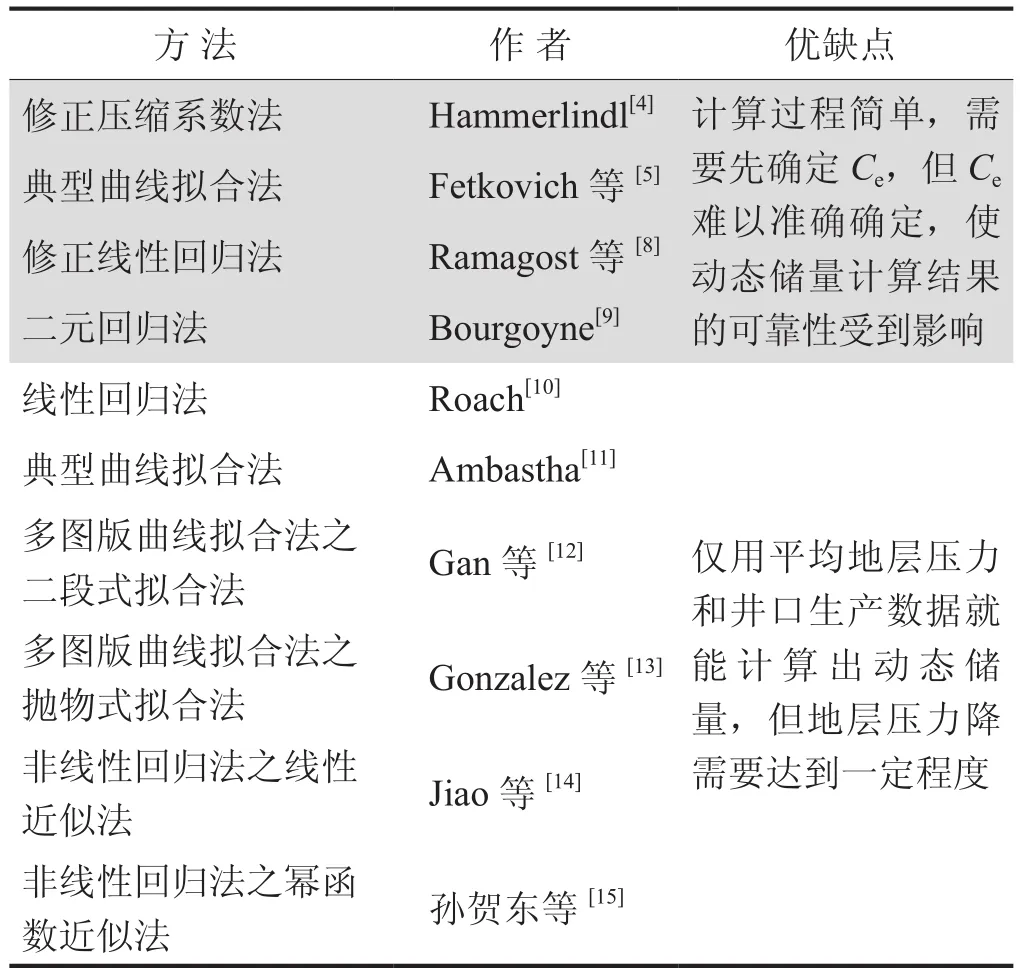
表1 计算高压、超高压气藏动态储量的物质平衡分析方法统计表

以图版拟合分析方法为代表的现代产量递减分析技术是评价气藏动态储量的新方法[16-18]，但也需要先确定Ce，因此不宜采用该方法计算高压超高压气藏的动态储量。

2.2 非线性回归法评价动态储量的起算点

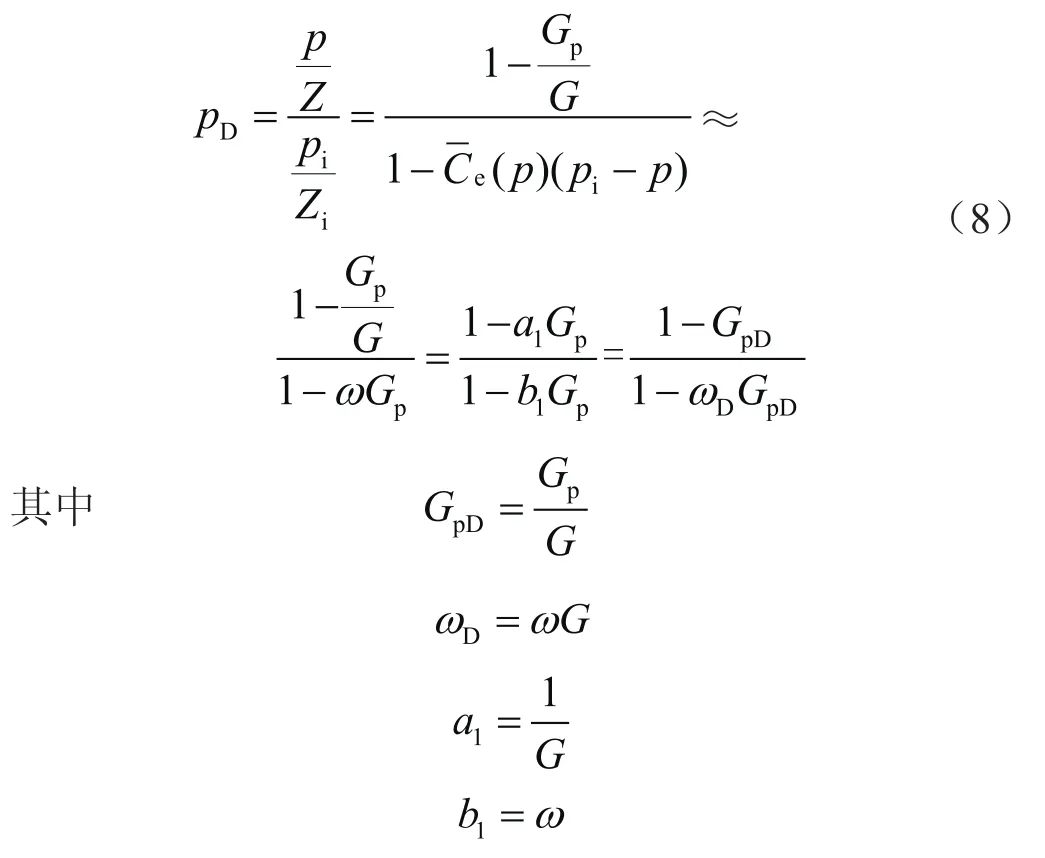
式中ω表示线性系数，(108m3)－1；a1、b1表示非线性回归系数，(108m3)－1。

ωD是的函数。若假设与GP符合幂函数关系[15]，且气藏无水侵现象产生，幂函数经验值为1.028 47，式（8）可以表示为：

对于产生水侵现象的气藏，幂函数经验值为1.115 67。计算实例表明幂函数经验值虽然来源于国外20个已开发中小型高压超高压气藏的统计分析，但对大型气藏也同样适用[15]。由此绘制出pD—Gp关系曲线，如图2所示，在开发早期，pD下降幅度较小，pD—Gp近似呈线性关系，将其回归结果称为视地质储量（Gapp），与G相比该值明显偏大；若pD下降幅度较大，pD—Gp呈非线性关系，a1、b1可通过非线性回归的方式得到，进而得到G。

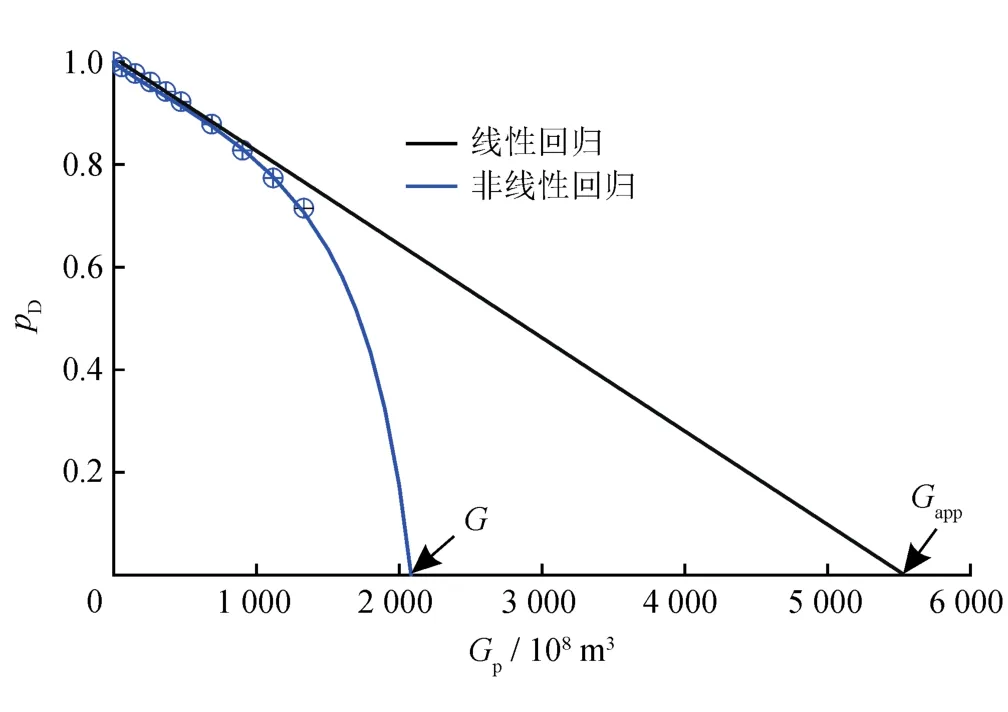
图2 某高压气藏pD—Gp数据点偏离早期直线段前后的线性、非线性回归曲线图

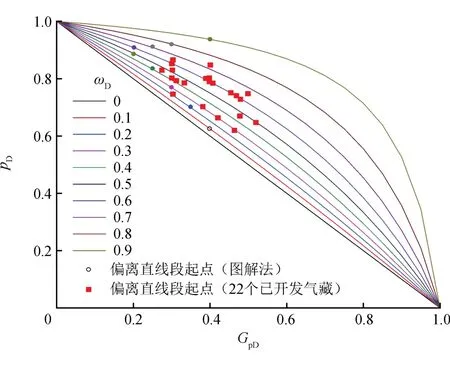
图3 pD—GpD曲线偏离早期直线段的起始点分布图

由于偏离pD—Gp曲线早期直线段的起始点无解析解，因此无法通过理论计算得到。根据式（8），绘制出pD—GpD关系曲线图版（图3），笔者采用图解法求取该点，先将pD—GpD早期数据点进行线性回归，进而确定线性回归曲线的斜率和截距，然后根据以下两个判别条件来共同判定拐点位置，分别为：①pD—GpD线性回归曲线的截距值与1.0的相对误差小于0.25%；②拐点横坐标GpD对应的pD线性回归拟合值和拐点实际pD值的相对误差小于0.50%。ωD取值不同，pD—GpD曲线偏离早期直线段的起始点位置差异明显，其对应的视地层压力衰竭程度（1－pD）介于0.06～0.38。对国内外22个已开发高压超高压气藏[15]进行统计，发现ωD介于0.20～0.75，偏离早期直线段的起始点对应的（1－pD）介于0.14～0.38，与笔者采用的图解法计算结果较一致（图3）。

如图3所示，对于处于试采早期的高压超高压气藏，即使试采时间长达1 a、压降幅度达到原始地层压力的3%～5%甚至更高，偏离早期直线段的起始点仍未出现，不能达到采用物质平衡法计算动态储量的起算条件。根据图3中不同ωD情形下pD—GpD关系曲线上偏离早期直线段的起始点，确定相应的数值；绘制关系曲线（图4-a）；采用线性回归，得到式（10），若采用非线性回归，得到式（11），即

统计分析国内外22个高压超高压气藏的开发数据[15]，得到关系曲线（图4-b），可以看出，关系曲线变化趋势基本一致。是ωD的函数，且与式（11）对应的

2.3 半对数典型曲线拟合法（未达到起算条件）

将图3中GpD采用常用对数形式来展示（图5），借鉴试井分析原理，采用图版拟合分析法来确定动态储量（G）。具体步骤如下：①基于实际生产数据，在pD—Gp半对数曲线图上绘制出系列数据点（Gp,pD），将其叠放在pD—GpD半对数典型曲线图版（图5）上；②上下移动数据点，使纵坐标轴对齐,然后左右移动数据点，使其与pD—GpD半对数典型曲线图版中某ωD对应的曲线拟合上，从而确定ωD，在此基础上，任取一点并分别读取其在pD—Gp、pD—GpD半对数曲线图上的坐标值（Gp,pD）、（GpD,pD）,进而根据前述式（8）中无量纲参数定义式计算得到G和ω；③若生产时间较短，对pD—Gp曲线图中数据点进行线性回归，求得Gapp，然后结合步骤②拟合得到的ωD，根据式（10）或式（11）确定进而得到G。

图4 pD—GpD曲线偏离早期直线段起始点对应的关系曲线图

图5 pD—GpD半对数典型曲线图版

3 实例分析

3.1 Anderson“L”气藏（达到起算条件）

美国Anderson“L”气藏中部埋藏深度为3 404.5 m，压力系数为1.907，采用容积法计算的气藏储量为19.68×108m3，生产数据详见本文参考文献[15]。该气藏虽然不属于超深层气藏，但属于超高压气藏，视地层压力衰竭程度（1－pD）为0.43，满足采用物质平衡法计算超高压气藏动态储量的起算条件。采用非线性回归法计算得到的动态储量为19.9×108m3（图6）。采用笔者提出的半对数典型曲线拟合法进行拟合，如图7所示，ωD拟合结果为0.4，在pD—Gp半对数曲线图上选取点m（2.0×108, 0.8），该点在pD—GpD半对数曲线图上的坐标为（0.1, 0.8），动态储量计算结果为20.0×108m3，计算过程为：

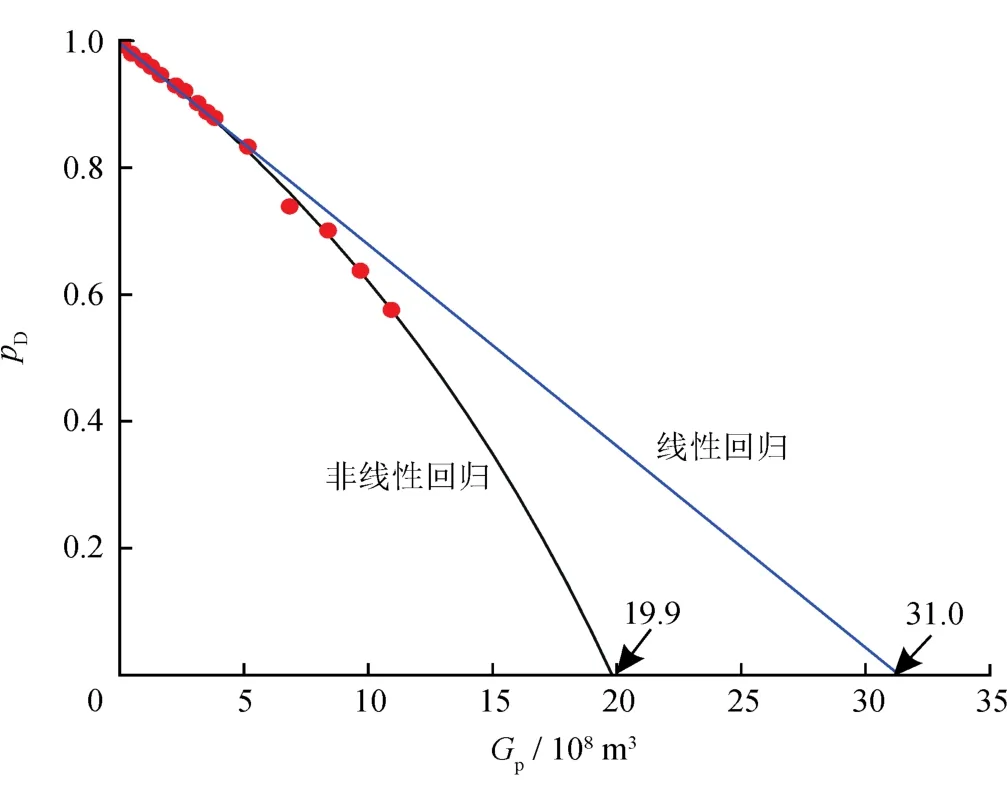
图6 Anderson“L”气藏pD—Gp数据点线性与非线性回归结果对比图

图7 Anderson“L”气藏pD—GpD半对数曲线拟合图

结合ωD的拟合结果（0.4），代入式（11）计算得到然后将pD—Gp曲线图中早期数据点进行线性回归，得到Gapp为31.0×108m3，从而得到G为20.4×108m3。该计算结果与采用其他方法计算的结果[15]基本一致，从而证实笔者提出的半对数典型曲线拟合法可靠。

3.2 迪那2气田（未达到起算条件）

迪那2气田产层位于古近系苏维依组与库姆格列木群，储层岩性以粉砂岩、细砂岩为主，属于低孔低渗储层，气藏中部埋藏深度为5 000 m，压力系数为2.16[19]。该气藏原始地层压力为105.89 MPa、地层温度为132 ℃；目前地层压力为79.04 MPa，累计产气量为426×108m3，视地层压力衰竭程度（1－pD）为0.11，不满足采用物质平衡法计算超高压气藏动态储量的起算条件。

采用笔者提出的半对数典型曲线拟合法进行拟合，如图8所示，ωD拟合结果为0.6，在pD—Gp半对数曲线图上选取点m（175.0×108, 0.8），该点在pD—GpD半对数曲线图上的坐标为（0.1, 0.8），动态储量计算结果为1 750.0×108m3，计算过程为：

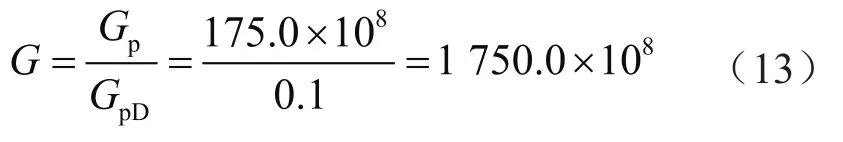
图8 迪那2气田pD—GpD半对数曲线拟合图

结合ωD的拟合结果（0.6），代入式（11）计算，得到然后将pD—Gp曲线图中数据点进行线性回归，得到Gapp＝3 750×108m3（图9），进而得到G＝1 751.2×108m3，与该气藏探明地质储量（1 704×108m3）较一致。

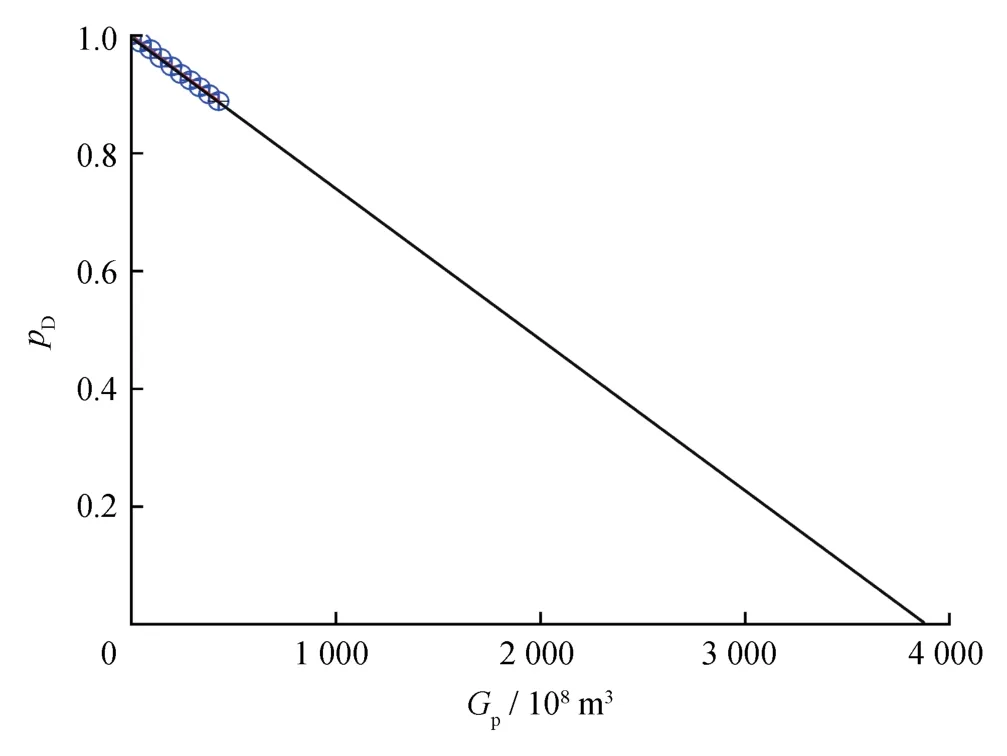
图9 迪那2气田pD—Gp数据点线性回归结果图

3.3 克深2气藏（未达到起算条件）

克深2气藏产层位于下白垩统巴什基奇克组，砂体厚度大，介于280～320 m，储层物性较差，岩心孔隙度介于2%～8%，平均值为4.1%，基质渗透率介于0.001～0.100 mD，平均值为0.05 mD[20]；气藏中部埋藏深度为6 640 m，压力系数为1.79[21-22]，在开发过程中气藏压力下降均衡、气产量递减快，表现出裂缝型储层的产出特征[23]；原始地层压力为116.42 MPa、地层温度为168 ℃，目前地层压力为84.45 MPa，累计产气量为95.8×108m3，单位压降产气量为3.0×108m3/MPa，视地层压力衰竭程度（1－pD）为0.10，不满足采用物质平衡法计算超高压气藏动态储量的起算条件。

图10 克深2气藏pD—GpD半对数曲线拟合图

采用笔者提出的半对数典型曲线拟合法进行拟合，如图10所示，ωD拟合结果为0.6，在pD—Gp半对数曲线图上选取点m（36.0×108, 0.8），该点在pD—GpD半对数曲线图上的坐标为（0.1, 0.8），动态储量计算结果为360.0×108m3，计算过程为：

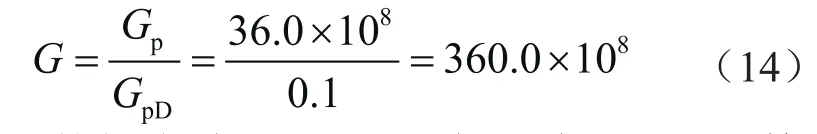
结合ωD的拟合结果（0.6），代入式（11）计算得到然后将pD—Gp曲线图中数据点进行线性回归，得到Gapp＝784.0×108m3（图11），进而得到G＝366.1×108m3，该数值与克深2气藏开发方案中的容积法储量（1 428×108m3）差异大。

图11 克深2气藏pD—Gp数据点线性回归结果图

图12 克深气田X井压力恢复双对数曲线图

由典型井的试井解释结果（图12）可以看出，压力导数曲线后期斜率介于0.5～1.0，测试400 h都未出现径向流特征，地层系数只有0.43 mD·m[23]，储渗空间类型为基质致密的裂缝型，基质对与井筒连通的裂缝系统的供气能力不强。同时，该气藏在关井检修的3个月期间，单井井底压力在0.5～2.0 h就迅速恢复到平均地层压力水平，但此后近100天关井期间平均地层压力仅上升了1.0 MPa，转换为pD则仅上升了0.01，也证实了基质的供给能力较弱。如图13所示，在开发早期该气藏的动态储量随累计产气量增大而逐渐增大，从早期的250.0×108m3增长到366.1×108m3；长时间关井后采用压降法计算Gapp＝ 875.0×108m3，相应G＝ 408.6×108m3，较之前仅增加42.5×108m3。当（1－pD）大于0.07后，动态储量基本保持稳定，即此时采出程度的提高对动态储量计算结果影响很小。