复合材料层合板冲击损伤等效模型研究
2020-08-11田媛杨宇王志刚张盛
田媛,杨宇,王志刚,张盛
(中国飞机强度研究所 陕西 西安 710065)
0 前言
复合材料因其比强度高和比刚度高、可设计性强等优良的性能在飞机结构中得到了广泛的应用,其应用的主要结构形式为层合板和加筋壁板,但复合材料层合板在冲击载荷作用下极易造成分层损伤。飞机复合材料结构在制造、安装和使用维护过程中,经常会受到冲击载荷,例如安装维护过程中工具的跌落,服役过程中的冰雹,起飞和着陆过程中跑道的沙砾,以及鸟撞等。受到冲击后,复合材料层合板内部容易产生基体开裂和分层等损伤,但低速冲击造成的损伤面积小,失效形式大多为层间分层。如果分层发生在中间层,这类损伤在日常检测中不易被发现,却会导致结构的强度大幅下降,严重削弱复合材料结构的承载能力,特别是压缩强度,继而影响其继续使用。因此,研究复合材料层合板的低速冲击损伤和剩余强度(CAI)问题对保证飞机复合材料结构的安全性至关重要[1]。
迄今对复合材料低速冲击及冲击后压缩问题已有较多的研究,但对冲击后层合板的压缩破坏机理并不完全了解,目前有4种压缩破坏分析方法。开口等效法,用一个圆孔或椭圆孔取代冲击损伤,之后用孔边断裂韧性等准则来判定层合板的破坏。子层屈曲法,将冲击损伤看作大小不同的多个规则形状的分层,认为压缩破坏过程是各个子层不断发生屈曲失效的过程,当所有子层都屈曲时,结构发生破坏。损伤累积法,利用动态有限元计算层合板的冲击损伤,以其对应的退化后的刚度作为层合板的初始损伤,再用损伤累积法模拟层合板的压缩破坏过程,并计算剩余压缩强度。软化夹杂法,将冲击损伤等效成规则形状的软化夹杂,然后用应力准则、应变准则或其他准则判定层合板的失效。
本文采用的方法为开口等效法。Qi和Ei-zein等认为可以把层合板的冲击损伤看作是含有椭圆孔或软化夹杂的含缺陷层合板,通过Lekhnitskii给出含有椭圆形夹杂的无限宽板的解进行剩余强度预测。Soutis和Curtis把层合板受冲击后的损伤近似看作一个圆孔,该方法可以成功地预测受冲击后背面有可见损伤的层合板的剩余强度。Avva和Padmanaha将冲击损伤模拟为一个嵌入的圆孔,根据动能和特征尺寸,应用平均应力准则得出预测剩余强度的表达式,进行剩余强度的预测[2]。本文研究了两种不同的计算复合材料层合板冲击后剩余强度的工程评估方法,并进行了试验验证。
1 改进的Whitney-Nuismer准则的层合板剩余强度评估方法
1.1 冲击损伤等效
一般地,低速冲击损伤可以等效为开口孔,等效孔几何形状为椭圆形,可以通过两个主轴的长度来确定,即2a和2b,如图1所示。实际中,真实损伤的尺寸2A和2B可以通过超声扫描确定。如图1所示。
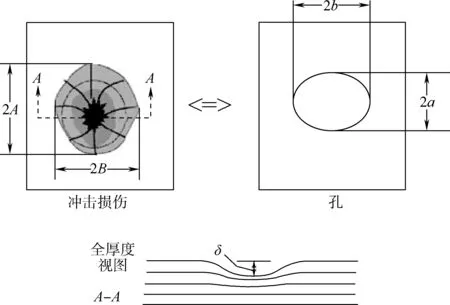
图1 冲击损伤等效为椭圆孔
在冲击后压缩的工况下,首先定义2b为垂直于压缩载荷方向的主轴尺寸,大小等于2B,2a为平行于压缩载荷方向的主轴尺寸,大小由下式确定:
(1)
当2a与2b相差不大时,可以将冲击损伤等效为圆孔(本程序以等效为圆孔来计算剩余强度,后续计算都以圆孔为例),如果2a与2b相差较大,仍然可以用该模型及准则,但需要将算法中孔边应力分布的表达式用各向异性弹性解表示。有了2a和2b,即可以应用带孔层合板剩余强度的计算方法进行评估。
1.2 带孔有限宽板剩余强度评估方法
1.2.1 无限宽板孔边应力分布
不考虑孔边损伤引起孔边应力重分布时,无限宽板孔边应力分布(θ=90 °时)由下式确定:
(2)
式中:
(3)
其分布如图2所示。
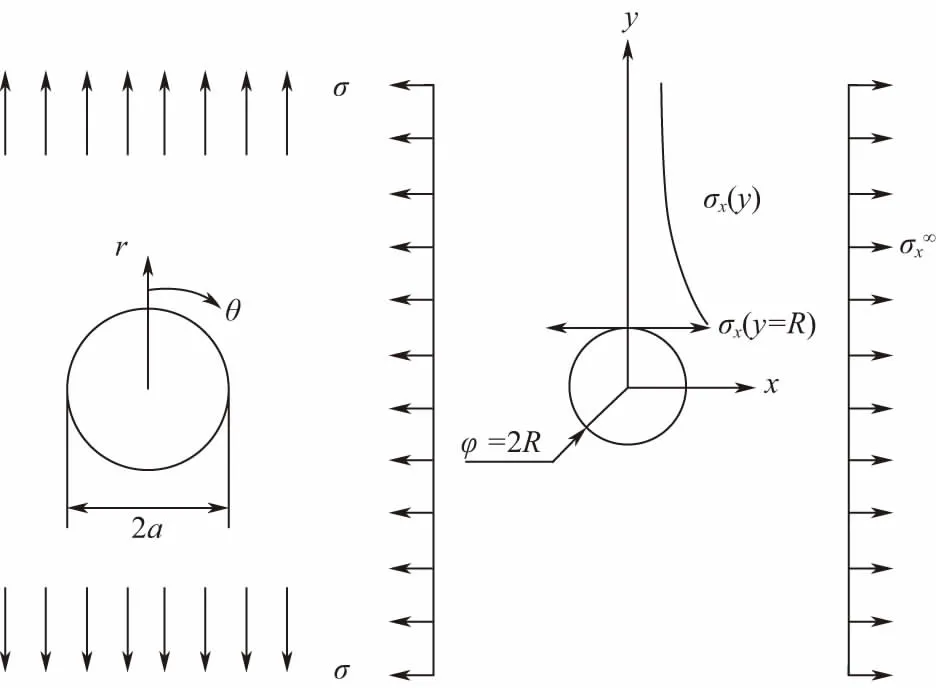
图2 带孔无限宽板拉伸坐标定义及孔边应力分布
1.2.2 带孔无限宽板失效判据——基本的Whitney-Nuismer方法
根据实际孔边应力分布,及A点与线性解垂直连接的假设,结合孔边应力分布的线性解,Whitney-Nuismer提出了点应力判据和平均应力判据:
(4)
其中:σf为无孔层合板的强度;d0和a0分别为点应力判据和平均应力判据对应的特征长度,该特征长度可以由试验确定,且只与层合板有关(材料、铺层等),在满足w/2-R>a0条件时,不同大小同一种层合板应具有相同的特征长度。满足上式时,对应的远场应力σ0即为该层合板的剩余强度[3]。
1.2.3 带孔有限宽板剩余强度评估——改进的Whitney-Nuismer方法
作为上一节基本Whitney-Nuismer方法的改进,本方法在于解析确定特征长度a0,而不需要通过试验计算,如图3所示,且考虑有限板宽的影响进一步改进剩余强度评估的精度。
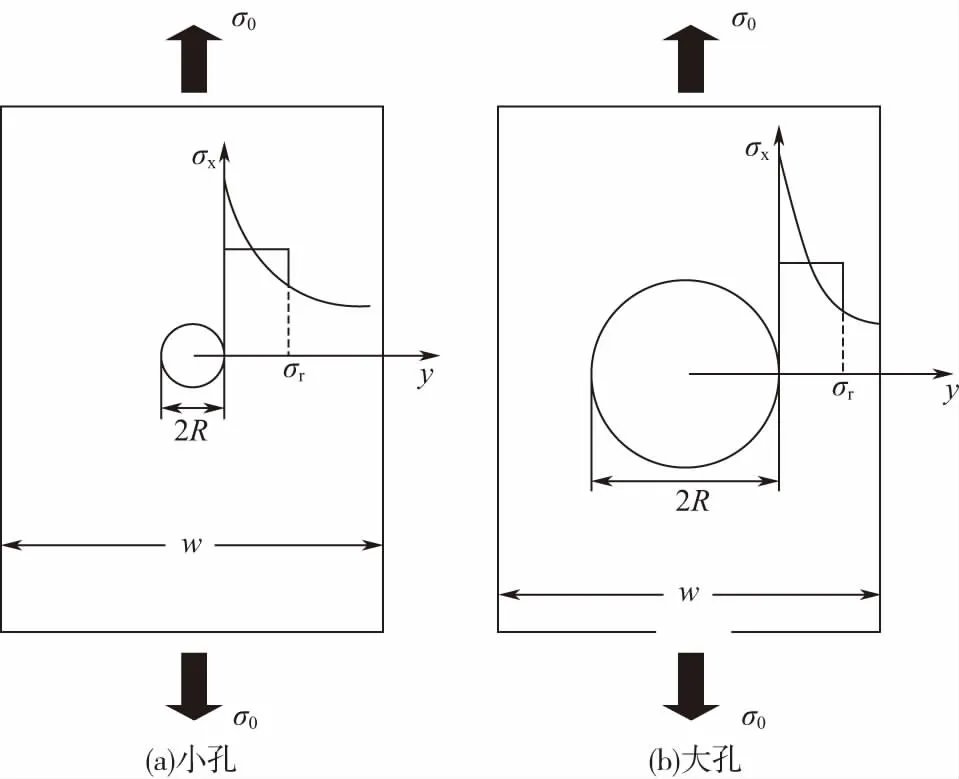
图3 不同大小孔的层合板拉伸
带孔有限宽板的应力分布根据无限宽板的结果进行有限宽度的修正,修正的原则主要基于无限宽板应力分布的两个重要特点决定:
σx(x=0,y),从y=R处到无穷远积分,其平均应力始终等于σ0。
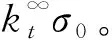
因此,有限宽板也必须遵守上面两个原则,但需要进行相应的修改以反映有限宽板的特点。故在有限宽板下两个特点修改为:
σx(x=0,y),从y=R处到w积分,其平均应力应等于σ0/(1-2R/w)。
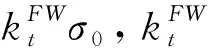
同时,假设带孔有限宽板的孔边应力分布与无限宽板孔边应力分布表达式具有相同的形式:
(5)
因此,为满足第一个要求,可得平均应力计算如下:
(6)
根据要求(a),σavg=σ0/1-2R/w,可得:
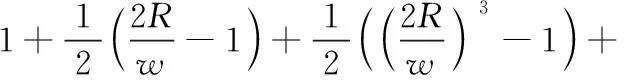
(7)
根据要求(b),可得:
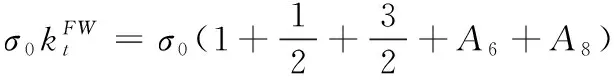
(8)
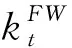
(9)
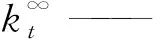
式(9)为一种较为精确的有限宽板孔边应力集中系数修正方法。至此,联立上述式(7)和式(8)即可求出系数A6和A8,最后得到有限宽板孔边应力分布表达式。
1.2.4 特征长度a0的确定
在上一节中提到,只要特征长度a0满足:w/2-R>a0,不同大小的同一种层合板具有相同的特征长度a0。因此,以极限情况为例,假设:
w/2-R=a0
上式可进一步表达为以下形式:
(10)
其中,s=a0/R。
在此条件下,根据Whitney-Nuismer模型,结构失效时,有限宽板平均应力即为无孔层合板的强度σf,在该拉伸工况下即为无孔层合板拉伸强度Ftu。从而Ftu可以表示为:
(11)
其中,A6和A8可根据之前方法计算确定,故为已知。但Ftu未知,且σ0不定。为了解析的求解特征长度a0,且不依赖于Ftu和σ0,需要引入Tan文献[4]中一种已知的求解带孔有限宽板的剩余强度计算公式,
将2R/w=1/(1+s)代入,联立上述两式即可得到:
(12)
式中,只有一个未知量s=a0/R。至此,通过求解式(11)得到s,最终可以确定特征长度a0的值。
因此,在该方法中特征长度a0的计算只与上述4个表达式有关,特征长度a0求解的本质即为联立求解式(7)~式(11)。如果将式(7)、式(8)中2R/w=1/(1+s)直接代入,则式(7)、式(8)可重新表示如下:
(13)
(14)
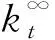
1.2.5 剩余强度的计算
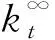
1.3 计算程序
将1.2节提出的改进的Nuismer-Whitney算法利用MATLAB进行编程,利用该程序计算有限宽度带孔复合材料板拉伸/压缩的剩余强度评估。程序流程图如图4所示。
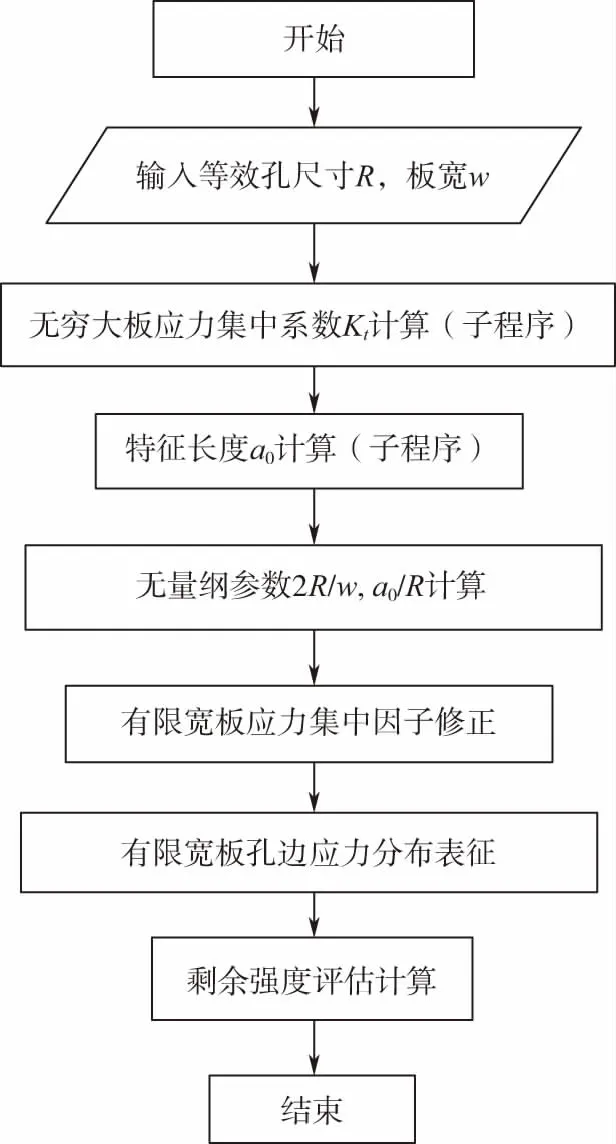
图4 程序流程图
2 基于同心圆损伤等效的层合板CAI剩余强度工程算法
对于冲击后损伤的区域,“刚度、强度折减法”是分析开孔板冲击后剩余强度的基础。本方法认为冲击区域的损伤可以由一连串的同心圆或者椭圆来模拟,同时损伤被等效为材料强度和刚度折减[4]。
2.1 应变计算
冲击后压缩状态如图5所示,损伤被模拟为不同大小的同心椭圆,边界施加均匀位移。

图5 同心椭圆损伤等效
可将面内的位移场级数展开,表示为如下的形式。
式中:P——待定参数;
H——待定参数;
x、y——坐标。
级数后面的一项是为满足边界条件加上去的一项,边界条件为:在板的两端,位移等于边界均匀位移u0;在板的两侧,满足泊松效应;位移函数还满足对称性条件,即沿两个对称轴(x,y轴)转角为零。Vxyeq为平均泊松比,如式(16)。i表示第i个区域,Area为对应区域的面积。
(16)
用最小位能原理可求出P和H。求解公式如下,其中,A为刚度。
(17)
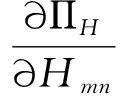
由此,可得位移场,从而得到复合材料板上的应变场,公式如下:
(18)
(19)
(20)
由此,可求得力:
2.2 损伤等效方法
利用损伤在厚度方向上的视图来确定板中等效损伤区域的尺寸。本方法将损伤区域等效为两个同心圆,其中内圆为纤维及基体均损伤,外圆为分层损伤,损伤区域以外的部分为完好区域。本文将无损检测结果应用到损伤区域的确定中,如图6所示,将无损检测结果中最中间色块的区域认为内圆区域,整个损伤区域的边界认为外圆的边界。

图6 基于无损检测方法的损伤区域等效
损伤区域的刚度、强度等效方法为:纤维失效,E11,Xt,Xc折减系数为1%;基体失效,E22,G12,Yt,Yc及S折减系数为5%。
2.3 失效准则
本方法的失效准则采用最大应力准则。该理论认为,各材料方向的主应力大于各自方向的强度时,材料发生破坏,刚度强度均折减为0。
2.4 计算程序
根据2.1、2.2、2.3节的方法编写了CAI计算的Matlab程序,该程序流程图如图7所示。
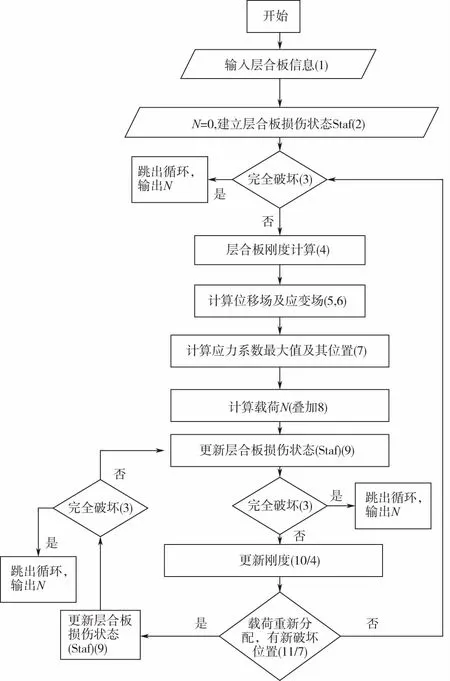
图7 基于同心圆损伤等效的matlab计算程序流程图
对等效为两个同心圆的损伤模型,当载荷达到某个值时,层合板某一层或者某几层纤维或者基体开始破坏。此时,对材料刚度进行折减,折减系数为0,载荷按刚度重新分配。若材料继续破坏,则刚度继续折减,载荷继续重新分配,直至未有新的破坏则继续施加载荷,此时根据更新后的刚度及2.1节方法重新计算应变,并判断新的失效载荷,直至所有层均发生破坏。需要注意的是,当外圆全部破坏后,内圆将不能承受载荷,此时认为内圆完全失效;同时,若外圆以外的区域每层均失效,则认为层合板完全失效。
3 算例应用
3.1 准各向同性层合板冲击后压缩强度试验
本次试验件层合板材料为CCF300/5428-5#上浆剂, 共6件试验件,试件尺寸为:150 mm×100 mm×4.8 mm,具体铺层为:[45 °/0 °/-45 °/90 °]2S,试验件性能参数见表1。

表1 试验件材料属性
将试件放置于冲击支持夹具中,以规定的能量对试件中心进行冲击,冲击时采用φ16 mm的半球形钢冲击头,冲击后测量试件表面的凹坑深度,并采用超声C扫描检测方法检测试件内部的损伤状况。冲击后压缩试验在疲劳试验机上完成。将冲击后的试件安装到压缩试验夹具中,进行静压缩试验,如图8所示。
3.2 试验结果与损伤扫描结果
试验结束后,超声C扫描检测6件试件内部的损伤状况如图9所示。
3.3 层合板剩余强度计算结果
根据超声C扫描结果,利用2.2、2.3节提出的两种剩余强度评估方法,分别计算了层合板剩余强度,结果见表2。

图8 冲击后压缩试验状态
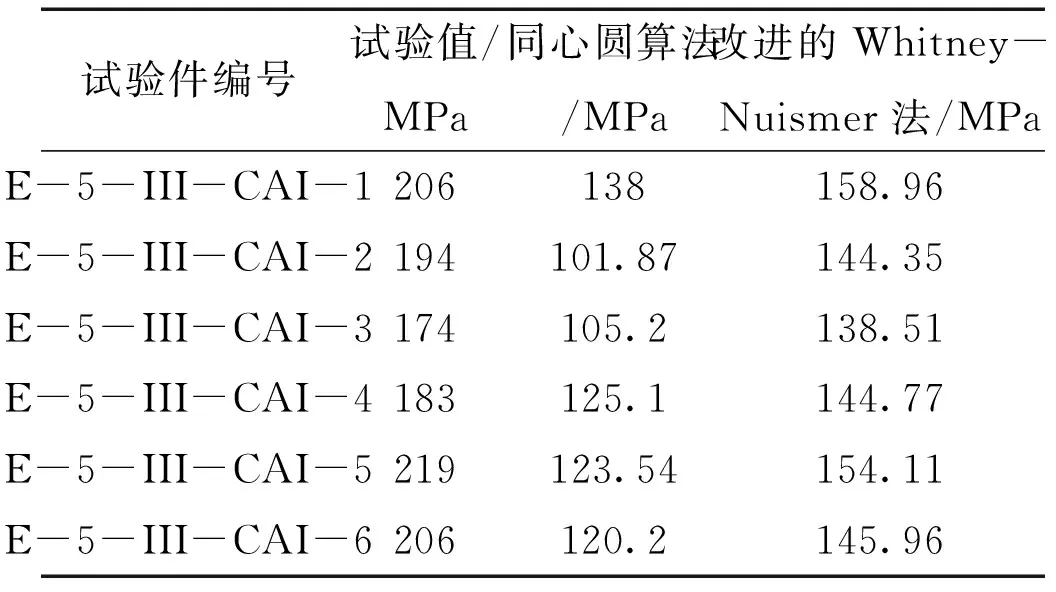
表2 层合板剩余强度计算结果

图9 超声C扫描图
4 结论
根据计算结果可以看出,两种层合板的剩余强度计算结果比实际试验值偏保守,对于改进的Whitney-Nuismer法,计算结果与层合板无损的破坏强度有关。而实际中,层合板的无损破坏强度是利用有限元程序计算得到。采用不同的失效准则,对于同一块层合板来说,结果的差异也是很大的,因此会造成CAI剩余强度结果的偏差。对于同心圆方法来说,同心圆半径的确定,位移函数展开级数等因素都将会影响最终计算结果的精度。
