基于单木断面积生长量的湖南栎类次生林立地评价研究

廖 波, 戴兴安

(1.华容县林业局，湖南 华容 414200; 2.中南林业科技大学，湖南 长沙 410004)

立地质量指某一立地上既定森林或者其他植被类型的生产潜力，是指导物种选择，设计造林指南和预测林分生长量的重要组成部分，准确评估立地质量是森林生态系统可持续管理的基本先决条件[1-3]。目前，同龄纯林的立地评价方法已经较为成熟可靠[4-7]，而异龄混交林的树种与年龄结构较复杂，同龄林的立地评价方法并不适用于异龄混交林的立地质量评价[8]。在全球气候变化的背景下，异龄混交林较之同龄纯林表现出更高的适应性和恢复能力[9]，因此异龄混交林的立地评价也引起了林业研究人员的重视，但目前尚无一种被普遍接受的异龄混交林立地质量评价方法[10]。

目前常见的立地质量评价方法包括立地指数(SI)[11]、树高-直径关系[12]、立地因子评价[13]、优势木高度生长量[14]等，但几种方法都存在一些不足，如立地指数的应用对象主要是同龄纯林，树木的高度与直径关系受林分密度影响，利用立地因子评价需要探讨立地因子与植物生长的关系，高度生长量的测量难度和误差较大。因此，选择一种合适的评价方法对于立地质量的评价至关重要。

胸高断面积生长量是反映树木生长状况的一个基本指标，其测量简单且误差较小[15-17]，是一个较为理想的立地评价指标。目前研究中尚没有依据胸径与胸高断面积生长量关系来评价异龄混交林立地质量的报道，可能原因是异龄林中林分或单木胸径的生长受林木竞争的影响较大。因此，本研究主要是以栎类次生林为研究对象，探讨利用栎类单木的胸径与胸高断面积生长量关系对栎类异龄混交林的立地质量进行评价。

1 研究区概况

湖南是中国中部省份，地理坐标为108°47′—114°15′E，24°39′—30°08′N。全省处于大陆性亚热带季风湿润气候带，地貌以山地和丘陵为主，土壤以红壤和黄壤为主，年平均气温16～19 ℃，年日照时间1 300～1 800 h，年平均降水量1 200 ～1700 mm[18]。湖南省植物类型多样，是中国植物资源最丰富的省份之一，其中栎类资源十分丰富，据统计的就有6属77种，较常见的有石栎属LithocarpusBL.、青冈属CyclobalanopsisOerst.和栎属QuercusL.。

2 材料与方法

2.1 数据来源

研究数据来源于湖南省森林资源连续清查固定样地，包括2004年、2009年和2014年共3期调查数据。样地数量为142块，面积大小为25.8 m×25.8 m，其中样地内的栎类树种株数占比均超过30%。利用GPS对样地的位置进行准确定位，同时对样地内胸径超过5 cm的树木进行详细调查，主要测树因子包括树高、胸径、树种、树龄、每公顷株数、郁闭度和相对指标等；样地记录的主要立地因子包括海拔、地貌、坡位、坡向、坡度、土壤、土壤厚度、枯枝落叶厚度以及腐殖质厚度等[19]。样地的基本情况见表1。

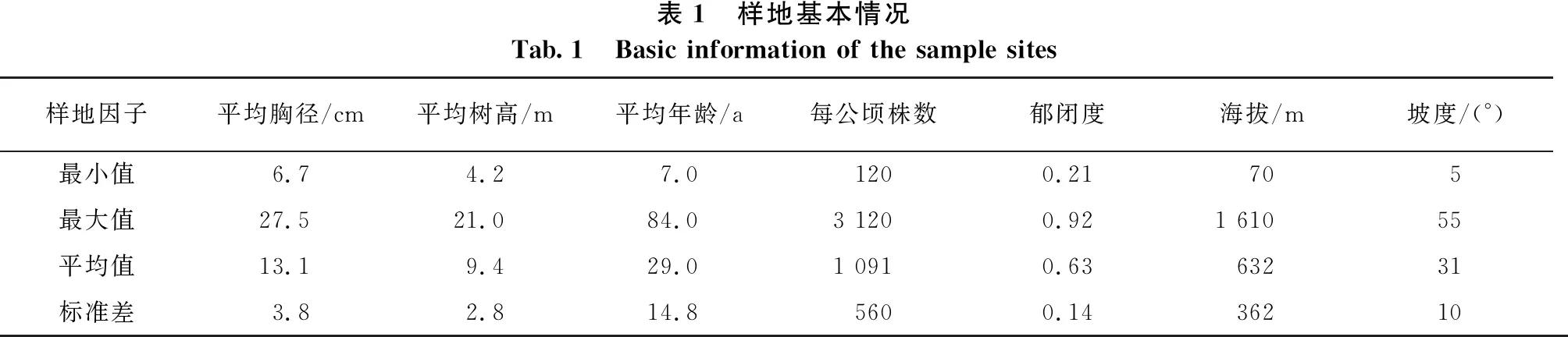
表1 样地基本情况Tab.1 Basic information of the sample sites样地因子平均胸径/cm平均树高/m平均年龄/a每公顷株数郁闭度海拔/m坡度/(°)最小值6.74.27.01200.21705最大值27.521.084.03 1200.921 61055平均值13.19.429.01 0910.6363231标准差3.82.814.85600.1436210

2.2 研究方法

参考地位级指数的编制方法，以湖南省2004年的栎类单木胸径与胸高断面积生长量数据为基础，建立以胸径为因变量，断面积生长量为自变量的导向曲线与标准差方程，并由此对单木生长进行分级，确定每株栎类单木的增长指数级，然后通过对单木的增长指数级进行加权平均的方法得出栎类样地的立地质量等级，并用湖南省2009年的栎类数据进行立地评价效果的检验。

同时，考虑到林木竞争对栎类胸径生长的影响，将探讨以下4种不同的栎类单木数据来进行立地质量的评价：林分中全部栎类优势木、林分中特定直径大小的栎类优势木、林分中全部栎类树木、林分中特定直径大小的栎类树木。

2.2.1 林分中优势木的确定方法 林分中优势木、平均木和劣势木所处的竞争状态不同，其生长速率可能存在差异。林木分级的方法包括有定性(克拉夫特林木分级法、寺崎渡林木分级法)和定量(相对直径法、竞争压力指数)方法[20-21]。其中，相对直径法[22]是根据树木直径与林分平均直径的大小关系对树木进行分级，该方法测量工作简便，但只考虑树木在林分中的优势状态，并未考虑到树木与相邻木的竞争状态。林分中对树木生长产生直接影响的应该是相邻木。惠刚盈[23]研究发现选取参照树及其周围 4株最近相邻木能够满足林分空间结构的分析，因此，本研究考虑用4株相邻木的平均直径代替林分平均直径，并用相对直径法对样地中的树木进行分级。相对直径法的表达式为：

d=r/R

(1)

式中:d为林木相对直径；r为林木胸径；R为4株相邻木平均直径；当d≥1.02时，可评定林木为优势木；当0.70≤d<1.02时，林木为平均木；当0.35≤d<0.70时，林木为劣势木。

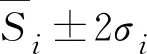
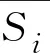
表2 模型基本表达式Tab.2 The expression of models理论模型表达式经验模型表达式Richardsy=a(1-e-bx)c对数曲线y=a+blg(x)Mistscherlichy=a(1-be-cx)幂函数y=axbGompertzy=ae-be-cx双曲线y=a+b/x

式中，y为因变量,x为胸径Di，a、b、c为模型参数。

(2)模型评价。模型评价采用确定系数(R2)、相对均方根误差(RRMSE)和平均预估误差(MPE)[24-25]，计算公式如下：

(2)

(3)

(4)

(5)

研究中，2004—2009年的样地数据用于增长指数级的确定，2009—2014年的样地数据用于立地评价精度的检验。

3 结果与分析

3.1 优势木与全部林木的生长量差异分析

为分析林分中优势木与全部林木的生长速率是否存在差异，本文运用t检验对不同径阶优势木与全部林木的胸高断面积生长量进行显著性差异分析。由图1可知，在6～26 cm径阶范围内，优势木的胸高断面积生长量高于全部林木的胸高断面积生长量；在6～20 cm径阶范围内，优势木与全部林木的胸高断面积生长量均呈增长趋势，22 cm径阶后趋于平稳；在6～12 cm径阶范围内，优势木的胸高断面积生长量显著高于全部林木的胸高断面积生长量；在14～20 cm径阶范围内，优势木与全部林木的生长量差异不显著。

3.2 利用不同组分数据进行立地评价

由图1的分析结果可知，栎类优势木与全部林木的胸高断面积生长量在6～12 cm径阶存在显著差异，在12～20 cm径阶不存在显著差异。同时，考虑到林木胸径达到30 cm以后，树木的胸高断面积生长量差异不大且测量误差较高，研究将栎类数据分为4种不同的组分：6～12 cm径阶范围内的优势木(Ⅰ类)；6～30 cm径阶范围内的全部优势木(Ⅱ类)；13～20 cm径阶范围内的全部林木(Ⅲ类)；6～30 cm径阶范围内的全部栎类林木(Ⅳ类)；并对比分析不同组分数据在评价立地时的效果。

3.2.1 数据分布特征与导向曲线拟合 对不同组分的胸径和胸高断面积生长量的分布特征进行分析，并绘制胸径与胸高断面积生长量的散点图(图2)。图2-a中，Ⅰ类数据中的栎类胸径数据近似于正态分布，胸高断面积生长量数据呈倒“J”形分布，且胸高断面积生长量随着胸径增大呈现增加的趋势；图2-b中，Ⅱ类数据中的栎类胸径数据近似于正偏态分布，胸高断面积生长量数据近似于负偏态分布，胸高断面积生长量随着胸径的增大未表现出明显增加的趋势；图2-c中，Ⅲ类数据中的栎类胸径数据近似于正偏态分布，胸高断面积生长量数据呈倒“J”形分布，胸高断面积生长量随着胸径增大而增加；图2-d中，Ⅳ类数据中的栎类胸径数据呈倒“J”形分布，胸高断面积生长量数据呈倒“J”形分布，胸高断面积生长量随着胸径增大而增加。Ⅰ类、Ⅱ类数据的胸径和胸高断面积生长量偏向于线性关系，Ⅲ类、Ⅳ类数据的胸径和胸高断面积生长量偏向于非线性关系。

利用6个模型拟合不同组分数据的胸径与胸高断面积生长量导向曲线，并运用t检验分析模型系数的显著性，结果见表3。Ⅰ类数据的最优导向曲线为Gompertz模型，其模型系数显著，R2最大，RRMSE和MPE最小；Ⅱ类数据的最优导向曲线为幂函数，其模型系数显著，R2最大，RRMSE和MPE最小； 6个模型在拟合Ⅲ类和Ⅳ类数据的导向曲线时，模型系数均具有显著性，Ⅲ类数据和Ⅳ类数据的最优导向曲线均为Gompertz模型，其模型系数显著，R2最大，RRMSE和MPE最小。

续表3 导向曲线的最优拟合结果Tab.3 The optimal results of guide curve fitting数据类型模型模型参数评价指标abcR2RRMSEMPERichards 0.010*(0.000 6) 0.144*(0.04)3.25*(1.18)0.9607.403.02Mistscherlich 0.011*(0.001) 1.419*(0.25)0.086*(0.02)0.9508.263.75Ⅲ类Gompertz 0.010*(0.0005) 4.567*(1.18)0.165*(0.03)0.9637.082.76对数曲线-0.007*(0.001) 0.012*(0.000 9)0.9389.535.00幂函数 0.000 8*(0.000 2) 0.768*(0.10)0.89012.218.20双曲线 0.012*(0.000 5)-0.064*(0.007)0.89611.907.79Richards 0.01*(0.000 5) 0.144*(0.029)3.599*(1.12)0.9726.522.20Mistscherlich 0.011*(0.001) 1.413*(0.21)0.080*(0.02)0.9617.733.10Ⅳ类Gompertz 0.01*(0.000 4) 5.007*(1.10)0.164*(0.02)0.9756.141.95对数曲线-0.008*(0.001) 0.012*(0.000 8)0.9508.733.95幂函数 0.000 6*(0.000 2) 0.827*(0.10)0.90412.127.60双曲线 0.011*(0.000 5)-0.065*(0.01)0.89812.568.17 注:*代表模型参数在α=0.05水平上具有统计学意义。下同。

3.2.2 标准差方程的拟合 利用6个模型拟合不同组分数据的胸径与胸高断面积生长量标准差的方程，并运用t检验分析模型系数的显著性，结果见表4。Ⅰ类数据和Ⅱ类数据的最优导向曲线分别为幂函数和双曲线，其模型系数显著，R2最大，RRMSE和MPE最小；Ⅲ类数据和Ⅳ类数据的最优导向曲线均为Gompertz模型，其模型系数显著，R2最大，RRMSE和MPE最小。

表4 标准差方程的最优拟合结果Tab.4 The optimal results of standard deviation equation数据类型模型模型参数评价指标abcR2RRMSEMPERichards 0.006(0.02) 0.053(0.22)1.221(1.38)0.9287.04 0.54 Mistscherlich 0.021(0.36) 0.999*(0.05)0.009(0.18)0.8708.82 0.85 Ⅰ类Gompertz 0.042(0.003) 2.64*(0.67)0.129(0.13)0.9306.96 0.53 对数曲线-0.002*(0.000 5) 0.004*(0.000 5)0.9057.89 0.68 幂函数 0.000 2*(0.000 05) 0.955*(0.11)0.9356.76 0.50 双曲线 0.004*(0.000 3)-0.014*(0.002)0.8549.34 0.95 Richards 0.006(0.01) 0.088(0.25)2.119(5.41)0.8136.78 1.06 Mistscherlich 0.007(0.01) 1.213 (1.52)0.050(0.17)0.8116.811.07 Ⅱ类Gompertz 0.005(0.003) 3.514(5.53)0.123(0.18)0.8146.76 1.05 对数曲线-0.005*(0.002) 0.007*(0.001)0.8126.80 1.06 幂函数 0.000 3*(0.000 1) 0.915*(0.18)0.8026.98 1.12 双曲线 0.006*(0.000 6)-0.051*(0.009)0.8156.74 1.05Richards 0.008(0.004) 0.036(0.037)1.119*(0.40)0.9587.33 1.40 Mistscherlich-0.009*(0.004) 1.015*(0.07)0.029(0.02)0.9577.35 1.40 Ⅲ类Gompertz 0.006*(0.000 9) 2.512*(0.35)0.084*(0.02)0.9587.26 1.37 对数曲线-0.003*(0.000 5) 0.005*(0.000 4)0.9398.78 2.00 幂函数 0.000 3*(0.000 06) 0.803*(0.06)0.9547.63 1.51 双曲线 0.005*(0.000 3)-0.028*(0.004)0.83114.61 5.54

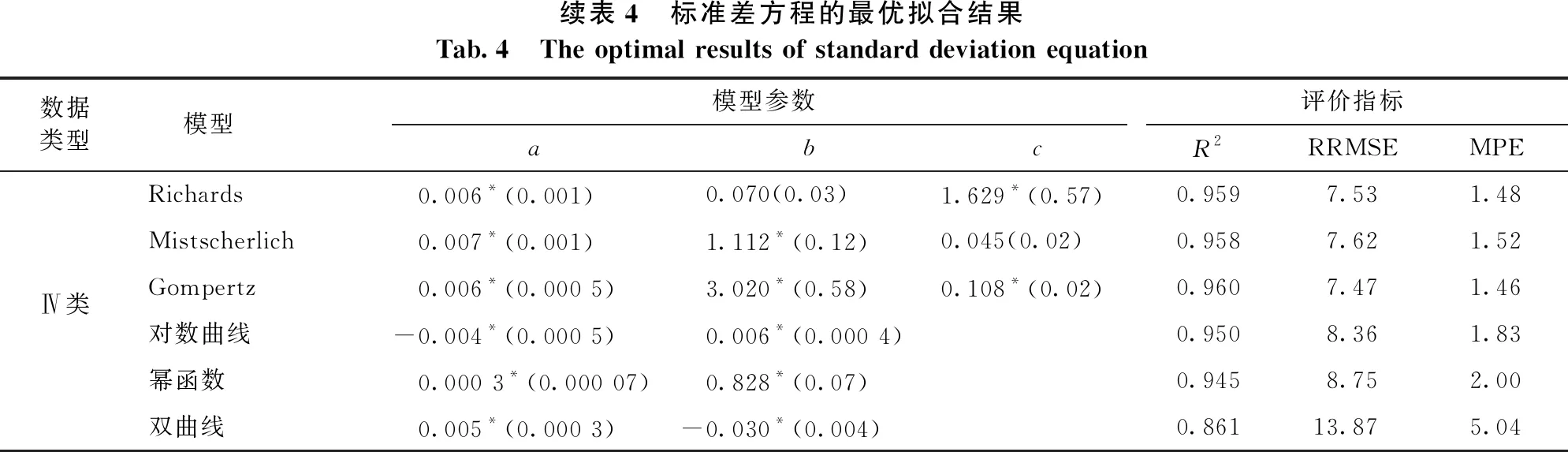
续表4 标准差方程的最优拟合结果Tab.4 The optimal results of standard deviation equation数据类型模型模型参数评价指标abcR2RRMSEMPERichards 0.006*(0.001) 0.070(0.03)1.629*(0.57)0.9597.53 1.48 Mistscherlich 0.007*(0.001) 1.112*(0.12)0.045(0.02)0.9587.62 1.52 Ⅳ类Gompertz 0.006*(0.000 5) 3.020*(0.58)0.108*(0.02)0.9607.47 1.46 对数曲线-0.004*(0.000 5) 0.006*(0.000 4)0.9508.36 1.83 幂函数 0.000 3*(0.000 07) 0.828*(0.07)0.9458.75 2.00 双曲线 0.005*(0.000 3)-0.030*(0.004)0.86113.87 5.04

3.2.3 增长指数级的确定 利用导向曲线与标准差曲线，依据Si±2σi原则，确定不同组分数据的增长指数级上、下限曲线；根据上下限曲线所夹的面积，采用等分方法将栎类单木的增长指数级分为5级，绘制不同组分生成的增长指数级曲线簇，如图3。利用Ⅰ类和Ⅱ类数据绘制的增长指数级曲线簇中，断面积生长量随着胸径的增加呈增长趋势，且存在较多样木数据超出曲线簇范围的现象；Ⅲ类和Ⅳ类数据绘制的增长指数级曲线簇中，断面积生长量随着胸径的增加而缓慢增长，最后趋于平稳，且超出曲线簇范围的现象较少。

3.3 评价精度检验与对比分析

依据增长指数级曲线簇的数据分布情况，计算出所有栎类单木的增长指数级，然后利用公式(5)计算出样地在2004年的立地质量等级，并采用2009年调查数据对样地的立地质量等级进行重新计算，对比分析前后2期样地的立地质量等级变化情况。结果得知，Ⅰ类、Ⅱ类、Ⅲ类和Ⅳ类数据在评价样地的立地质量时评估精度分别为66.7%、56.2%、63.3%和78.2%，可知利用Ⅳ类数据，即样地内所有栎类林木的胸径与胸高断面积生长量关系对栎类样地进行立地评价的精度最高，达到78.2%。

4 结论与讨论

4.1 讨论

与传统方法相比，本研究利用树木的胸径与胸高断面积生长量关系对立地质量进行评价，具有一定的优势。树木树高与胸径的生长渐进值在同一立地当中不是固定不变的，它可能随着气候以及经营措施的改变而发生变化[26]，而利用树木一定时间内的生长量对立地进行评价，可以动态的反映出气候以及经营措施对立地质量的影响。传统方法通常是利用优势木的年龄—树高进行立地评价[27-28]，而年龄与树高的确定难度较大，且在测量当中容易出现系统误差。胸径的测量工作相对简单且误差较小，在考虑林木竞争对胸径生长影响的前提下，将是一个合适的替代指标。

在利用胸高断面积生长量进行立地评价时，需要解决的关键技术是林木竞争对树木生长的影响，因为林木竞争对树木树高和胸径的影响是普遍存在的[29-30]。一些研究认为，当只考虑林分中的优势木时，林木竞争对树木树高与直径的关系影响很小[31]，这可能是减少林木竞争影响的有效方法。而本研究在对比分析了4类数据对评价立地质量的效果后发现，在不考虑林木优势状态的情况下，该方法的立地评价效果更好。可能原因是，异龄林当中的树木生长抑制现象普遍存在，即使是优势木也无法保证幼龄时期未受到林木竞争影响，而研究提出的方法充分考虑了每株树木的生长量信息，是对林分平均生长速率的良好反映。

立地指数是反映树木在立地上最大生长潜力的绝对性指标，而本研究提出的增长指数级是反映树木在立地上生长速率的相对性指标，具有一定的局限性。该方法需通过样地的连续监测或解析木获取胸径生长量数据，存在工作周期较长的问题。但湖南省设置有6615个监测周期在30年以上的固定样地，胸径与胸径生长量数据很容易获取。在目前异龄混交林立地评价尚无一种较好方法的前提下，该方法可作为一种评价湖南栎类异龄混交林立地质量方法的有效尝试。

4.2 结论

本研究提出一种基于胸径与胸高断面积生长量关系，运用单木增长指数级推算样地立地等级的评价异龄混交林立地质量的方法，在对比分析了4种不同类型数据对评价立地质量的效果发现，利用林分中全部栎类树木的胸径与胸高断面积生长量关系评价立地质量的效果最好，该方法精度能达到78.2%，可为异龄混交林的立地质量评价提供参考。