多种智能算法求解不同规模的TSP 问题分析

段双双

1 TSP 问题描述

TSP 问题（Traveling Salesman Problem）又称为旅行商推销员问题，是一个易于描述但难于解决的问题之一。TSP 问题已知n 个城市各城市间的距离，某一旅行商从某个城市出发访问每个城市一次且仅一次，最后回到出发城市，怎样安排才使其所走路线最短[1]。由于TSP 问题代表一类组合优化问题，在实际工程中有许多应用，如产品的生产安排、计算机联网、电子地图、交通诱导、电气布线、VLSI 单元布局、AT M 分组交换网等。因此TSP 问题的求解具有重要的理论意义和实际意义[2]。

2 TSP 问题的数学模型

2.1 TSP 问题可以用以下数学模型来描述

设有一个城市集合C=（c1，c2，…，cn），其中每对城市之间的距离，求一对经过C 中每个城市一次的路线，使：

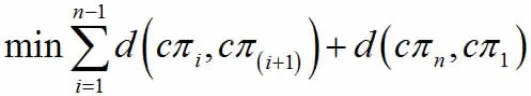
3 智能算法求解TSP 问题

TSP 问题被证明是一个NP- hard 问题，即在P≠NP 的假设下，找不到一个多项式时间算法来求解其最优解。自1932 年提出以来，已引起许多学者的兴趣，但至今尚未找到非常有效的求解方法。

解决TSP 常用的方法有两类，一是传统的确定性算法，如动态规划DM，分支限界法LC等。第二类是现在流行的智能算法，如蚁群算法(ACA)[5]，遗传算法(GA)，模拟退火(SA)，禁忌搜索(TS)，神经网络(NN)，粒子群优化算法(PSO)，免疫算法(IA)等[4]。本文就模拟退火，禁忌搜索，遗传算法，蚁群算法对n 为30，50，75 三种不同规模的TSP 问题进行求解。

3.1 部分参数设置

3.1.1 城市数目为n，城市坐标如下：

n=10 city10= {（0.4，0.4439）（0.2439，0.1463）（0.1707，0.2293）（0.2293，0.761）（0.5171，0.9414）（0.8732，0.6536）（0.6878，0.5219）（0.8488，0.3609）（0.6683，0.2536）（0.6195，0.26 34）}

n=30 city30={(41 94)(37 84)(54 67)(25 62)(7 64)(2 99)(68 58)(71 44)(54 62)(83 69)(64 60)(18 54)(22 60)(83 46)(91 38)(25 38)(24 42)(58 69)(71 71)(74 78)(87 76)(18 40)(13 40)(82 7)(62 32)(58 35)(45 21)(41 26)(44 35)(4 50)}

n=50city50={(31 32)(32 39)(40 30)(37 69)(27 68)(37 52)(38 46)(31 62)(30 48)(21 47)(25 55)(16 57)(17 63)(42 41)(17 33)(25 32)(5 64)(8 52)(12 42)(7 38)(5 25)(10 77) (45 35) (42 57) (32 22) ( 27 23) (56 37)(52 41)(49 49)(58 48)(57 58)(39 10)(46 10)(59 15)(51 21) (48 28) (52 33) (58 27) (61 33) (62 63)（20 26）（5 6）（13 13）（21 10）（30 15）（36 16）（62 42）(63 69)(52 64)（43 67）}

表 1 SA，TS，GA，ACS 四种在 n=30，50，75 三种情况下求解结果

n=75city75={（48 21）（52 26）（55 50）（50 50）（41 46）（51 42）（55 45）(38 33)(33 34)(45 35)(40 37)(50 30)（55 34）（54 38）（26 13）（15 5）（21 48）（29 39）（33 44）(15 19)(16 19)(12 17)(50 40) (22 53) (21 36) (20 30) (26 29)（40 20）（36 26）（62 48）(67 41)(62 35)(65 27)(62 24)(55 20)(35 51)(30 50)(45 42)(21 45) (36 6) (6 25) (11 28) (26 59) (30 60)（22 22）（27 24）（30 20）（35 16）（54 10）（50 15）（44 13）（35 60）（40 60）(40 66)(31 76)(47 66)(50 70)(57 72)(55 65)(2 38)(7 43)(9 56)(15 56)(10 70)(17 64)(55 57)(62 57)(70 64)(64 4)(59 5)(50 4)(60 15)(66 14)(66 8)(43 26)}

3.1.2 参数设置

模拟退火（SA）算法参数：tf=0.01，alpha=0.80，L=100*Ci tyNum

禁忌搜索（TS）算法参数：cl=100，tl=50，l1=200

遗传算法（GA）算法参数：inn=100，gnmax=1000，pc=0.8，pm=0.08

蚁群算法（ACS）算法参数：Alpha=1，Beta=5，Rho=0.5，NC_max=200，Q=100

Hopfield 神经网络算法（HNN） 算法参数：A=500，B=500，C=200，D=500，arf=1，miu0=0.02，lan=0.00001，EndNum=1000。

3.2 算法运行结果

运用matlab7.0 版本进行编程计算[7]，分别用模拟退火，禁忌搜索，遗传算法，蚁群算法4 种智能算法求解n=30，50，75 的tsp 问题结果对比如表1 所示。

3.3 结果分析

从表1 可以看出，综合来说，SA 迭代搜索具有较强的局部寻优能力并且能使搜索过程避免陷入局部最优解，而且具有高效、鲁棒、通用、灵活的优点，但在前期搜索过程较难最有希望的搜索区域，从而全局最优解难于找出，运算效率不高；TS 解决规模较大组合优化问题时，单纯应用频率记忆或改变参数来实现多样性搜索有可能得不到理想的效果；GA 可大大减少陷入局部最小的可能，但相对其他三种算法主要缺点是搜索空间大，导致搜索时间比较长；ACS 虽然能快速找到最优解，但是很容易陷入局部最优的缺点[6]。综合来说，对于 SA，TS，GA，ACS 这四种算法，都比较适合较大规模的TSP 问题求解，从最短距离和达到最优解的速度来看，解决TSP 问题，蚁群算法会更优于其他三种算法。

4 结束语

本文是用最基本的4 种智能算法对不同规模的TSP 问题进行求解，然后对他们的求解结果进行比较分析，以后会从这些算法本身或是将多种算法相结合这两个方面一定的优化工作，能更好的求解TSP 问题，进而将这些算法应用到其他的工程实际问题上。