多种聚类算法性能的比较分析

纪汉霖，李兆信

(上海理工大学，上海 200093)

0 引 言

聚类是重要而基础的数据分析和挖掘的算法，在金融、教育、医疗、互联网等方面有着广泛的应用。聚类属于无监督学习范畴，在没有数据标签的条件下，可以依据数据之间的相似度(如距离)对数据进行先验的分组，从而使得分组内的数据相似度尽可能高，分组之间的数据差异度尽可能大。

聚类算法在人工智能热潮的推动下飞速发展，算法的种类不断增多。如何为不同类型的数据集匹配恰当的聚类算法进而挖掘出数据集中的有效信息，是当下研究的热点与难点，因此对聚类算法在不同数据类型中的效能和敏感性的对比分析是一个值得研究的课题。

1 聚类算法的分类

自Lawrence Hubert[1]于1972年提出聚类算法至今已经将近半个世纪，在这几十年中学者们已经提出了上千种聚类算法[2]。聚类算法通过结合各个学科的技术和特点，融合发展为一个跨学科的方法，进而可以通过多种视角和方法对聚类算法进行归类。聚类算法可以分为传统方法和新方法两大类，传统的划分有层次聚类(HC算法和Birch算法)、划分式聚类(K-means)、基于密度的划分(DBSCAN)、基于网格的划分等(以STING和CLIQUE为代表)，近年来也有一些新发展的方法：基于约束的划分、基于模糊的划分、基于粒度的划分、量子聚类、核聚类、谱聚类[3-5]，如图1所示。

图1 聚类算法的分类示意图

以上这些算法大多是基于数据的特性而衍生出来的，导致算法对很多数据类型的适用效果并不好。因此在聚类研究中，学者们更侧重于在特定数据集的基础上对算法进行研究和改进。刘晓勇等(2011)[6]通过在AP算法中加入收缩因子，在服从[0,1]上均匀分布的模拟数据点上验证了相关改进能够加速算法的收敛速度。赵玉艳等(2008)[7]通过在BIRCH算法中加入ID传播并改进近邻密度的计算方法，在Manku GS和Motwani R(2002)[8]的DSI数据集上验证了相关改进能够加强算法的伸缩性并提高算法准确度。胡庆辉等(2013)[9]通过对GMM算法的系数中加入熵惩罚因子，在基于高斯分布而生成的人工数据集上验证了相关改进能够加快迭代速度并且可以提高鲁棒性。陈黎飞等(2008)[10]通过构建聚类质量曲线确定层次聚类的聚类数目，在真实数据和人工合成数据集的基础上验证了相关改进能够对数据进行更好的划分。周林等(2012)[11]通过在谱聚类算法中使用连接三元组算法，在由加州大学UCI(University of California Irvine)数据库中选取的数据集上验证了相关改进能够提高簇内数据相似度和计算效率。周爱武等(2011)[12]通过提出一种新的方法来确定K-means的聚类中心，在由UCI数据库中提供的数据集上验证了相关改进能够降低孤立点对算法的影响。

在算法性能方面，之前的学者主要是对AP、Birch、GMM、HC、K-means等主流聚类算法在特定数据集上进行相关改进和研究，然而却很少对算法在不同数据集上的表现进行相应的研究。即使在对算法进行横向研究比较时，选用的数据测试集也多是来自加州大学UCI数据库(UCI数据库由真实数据生成的标准测试集组成)。冯晓蒲等(2010)[13]使用UCI数据库中的IRIS对K-means、层次聚类、SOM和FCM四种算法做了对比研究，结果显示FCM和K-means的聚类效果比较好，层次聚类算法的聚类效果最差，SOM的效率最低。与之前学者研究不同的是：文中利用由机器生成的数据集对算法进行横向的研究，数据类型分为三类：离散型小数、离散型整数和连续型正数。

对比分析了Affinity Propagation、Birch、Gaussian Mixture Model、Hierarchical clustering、K-means和Spectral六种聚类算法，采用Silhouette Coefficient和Calinski-Harabaz Index为聚类评价指标对算法做了性能测试，采用算法在数据集上CPU消耗的时间作为评价指标对算法做了效率测试，以及在由不同数量级组成的数据集上对算法进行了敏感性分析。

2 聚类算法概述

(1)Affinity Propagation聚类算法。

AP算法是由Frey B J和Dueck D于2007年在科学杂志上最先提出来的聚类算法[14]，之后一直受到后来学者的关注与研究。AP算法对数据的特性没有要求，数据集结构可以是对称的也可以是非对称的。AP算法不需要提前设定聚类中心的个数，因为该算法把数据集中的数据点作为潜在的聚类中心，通过算法的不断迭代确定出聚类中心的数据点。

该算法通过计算出数据点之间的相似度，利用相似度组成方形矩阵，方阵对角线的值称为参考度，参考度越大表示对应的数据点成为聚类中心点的概率越大。AP算法通过一种数据点和潜在聚类中心点互相选择的机制来实现聚类，数据点通过计算发送到各个潜在聚类中心点的信息来决定自己属于哪个簇，同样的聚类中心也通过计算发送到各个数据点的信息判断哪些数据点属于本簇，在不断的迭代下确定聚类的个数和聚类中心数据点。

(2)Birch聚类算法。

Birch算法是由Zhang T等在1996年提出的一种分层聚类算法[15]。算法使用聚类特征CF树结构对数据点进行聚类。CF树是由算法对不同子树赋予不同的权重而组成的，每个子树中包含一个特征元组，特征元组由数据点数、点与点之间的线性和点与点之间的平方和组成，因此CF树中拥有每个子树的特征统计信息。CF树通过最大子树的个数确定聚类个数，每个子树中数据点与聚类中心之间的最大距离确定该数据点是否属于本树。在CF树自上而下的扫描过程中，由于其拥有每个子树的统计信息，所以不需要把所有数据都读取到内存中，正是基于这个特性使得Birch算法能够处理大规模的数据量。CF树动态的特性使其能把读取的新数据点插入到最近的子树中，如果新的数据点的直径超过了阈值，就会重新新建一棵子树。通过元组的统计信息对数据集进行分类，然后在这个基础上对新读取的数据进行聚类，这使得消耗I/O时间相对其他分层算法要小。

(3)Gaussian Mixture Model聚类算法。

高斯混合模型采用概率为标准衡量数据之间的相似度。算法假设数据集是由一定数量的具有高斯分布特性的数据组成的，然后将数据点的协方差与高斯中心结合起来，进而实现GMM拟合的期望最大化。算法利用贝叶斯准则对数据进行随机分类，然后计算每个数据点是由高斯分布模型生成的概率，在多次迭代调整参数后，最大化给定这些数据点的概率，进而为每个簇里分配最符合其高斯分布的数据[16]。

(4)Hierarchical聚类算法。

HC聚类主要分为自下而上的凝聚层次法和从上到下的分裂层次法，前者簇的数据点是从少到多依次合并直到满足一定的条件而终止，后者是把数据点逐渐细分为小的簇，直到满足条件不再细分而终止。文中使用的是scikit-learn的HC算法，其属于凝聚分层法。算法先把每个数据点分为一类，然后利用相似度把两类并成一类，不断迭代，最后合并为K类。

(5)K-means聚类算法。

K-means算法在1955年最先由Steinhaus提出，之后其他领域也有学者在各自科研领域提出，直到1967年MacQueen[17]对前人的研究进行总结完善，并且给出了数学证明，使得K-means算法被广泛应用。算法利用距离作为相似度的评价准则，通过不断迭代使聚类中心点与簇内数据点的距离尽可能小。文中使用的是K-means++，该算法在数据集中随机取一个数据点作为簇的中心点，然后计算其他数据点到聚类中心点的距离，距离越大所对应的数据点有可能成为下一个簇的中心点，通过不断迭代确定K个聚类中心点，这样就避免了其对聚类中心初始值选定的敏感问题。

(6)Spectral聚类算法。

谱聚类是一种基于对图谱划分的算法(2008)[18]，该算法对数据的空间形状没有要求。算法把数据集转换为矩阵，通过计算矩阵的K个特征值和特征值对应的特征向量，使其组成一个特征向量空间，利用特定的划分规则，比如基于距离的划分规则，在多次迭代之后使簇内数据点的权重大(相似度高)，簇与簇之间的权重小(相似度低)。

综上所述分析，文中选取数据属性、时间复杂度、算法伸缩性、算法对噪声的敏感程度、处理高维数据的能力、对复杂形状的数据集是否适用这六个指标，对上述六种算法的性能进行了总结，如表1所示。

表1 部分聚类算法性能总结和比较

3 聚类有效性指标概述

由于文中的数据都是无标签的，所以采用内部评价标准，利用数据集和聚类结果生成的标签对聚类效果进行评估。小组内的数据相似度越高，小组与小组数据差异度越大，说明数据被很好地归类。常用的评价指标有Silhouette Coefficient和Calinski-Harabaz Index。

3.1 Silhouette Coefficient

3.2 Calinski-Harabaz Index

Calinski-Harabaz Index是由Calinski和Harabaz[20]于1974年提出的一种评价指标。CH系数：

其中，K表示聚类中心的个数，tr(Bk)表示簇与簇之间离差矩阵的迹，tr(Wk)表示簇内离差矩阵的迹。Bk表示簇与簇之间的协方差矩阵，Wk表示簇内协方差矩阵。CH评分是簇间分离值与簇内分离值之值，比值越大代表聚类效果越好。

4 实验测试及分析

本节利用数据的差异对Affinity Propagation、Birch、Gaussian Mixture Model、Hierarchical clustering、K-means和Spectral算法的聚类效果和效率进行了综合实验评估。所有算法由Python实现，Python的版本是Python 3.7.2，sklearn的版本是scikit-learn v0.21.1，实验平台采用Intel(R)Core(TM)i5-4210M CPU @ 2.6 GHz，8 G内存，Windows 10企业版。

4.1 实验数据和测试方法

实验数据均属于机器数据，主要分为两大类：连续型数据和离散型数据。其中连续型数据分为七类，离散型数据分为离散小数和离散整数两类。具体信息如表2所示。

表2 数据描述

4.2 测试方法

为了探究聚类算法的有效性，对Affinity Propagation、Birch、Gaussian Mixture Model、Hierarchical clustering、K-means和Spectral算法分别在13类基准数据集上进行了测试。因为以上算法均属于无监督算法，所以聚类效果的评估使用了Silhouette Coefficient(以下简称轮廓系数)和Calinski-Harabasz Index(以下简称CH评分)，使用聚类算法消耗的时间作为算法效率的评价指标，并且探究了算法对数量级的敏感性分析。

4.3 效果评估

为了保持一致性，被测试算法被设定为四个聚类中心。其中Affinity Propagation 算法的preference=-50、Gaussian Mixture Model算法的covariance_type为'full'、K-means算法的内核为K-means++，random_state=28。

如图2所示，为了区分，采用不同的形状表示不同的算法。

(a)离散型小数

(b)离散型整数

(没有AP算法的局部图)

4.3.1 数据只有行数增加时

当数据集为离散数据时，从图2(a)和(b)中可以看出，在轮廓系数中聚类效果随着行数的增加而变差，CH评分中聚类效果随着行数的增加而变好，在两种评价指标下聚类效果最好的是K-means；当数据集为连续型正数时，从图2(c)中可以看出，Birch、GMM、HC、K-means和Spectral的聚类效果在CH评分中很接近，AP算法大约在20行以上的聚类效果随着行数的增加其CH评分远远高于其他五种算法，这主要是因为AP算法对数据的初始值不敏感，并且其聚类中心是数据集中的点，而不是由算法生成的中心点。然而在轮廓系数中，AP算法的评分反而是一个比较固定的值，且表现不如其他算法，这是因为AP算法的聚类中心点为已有数据点，数据的特性导致簇与簇之间的平均距离和簇内平均距离比较固定，进而使得轮廓系数的值随行数的变动很小。

4.3.2 数据只有列数增加时

当数据集为离散数时，被测试算法的聚类效果随着列数的增加而变差。从图3(a)中可以看出，当数据集为离散型小数时，算法在两种评价指标下的聚类效果很接近，其中Spectral算法随列数的增加波动性变大，而其余算法则比较稳定。从图3(b)中可以看出，当数据随集为离散型整数时，算法在两种评价指标下聚类效果很接近，其中HC算法随列数的增加波动性变大，而其余算法则比较稳定；当数据集连续型正数时，从图3(c)中可以看出，在两种评价标准中，被测试算法的聚类效果中除了Spectral算法其余算法基本不受列数变动的影响，而且被测试算法的聚类效果在两种评价标准中表现不同。在CH评分下被测试算法聚类效果最好的是AP，其次是K-means，在轮廓系数评分下被测试算法的聚类效果从好到差排名是：HC、K-means、GMM、Birch、AP。

(a)离散型小数

(b)离散型整数

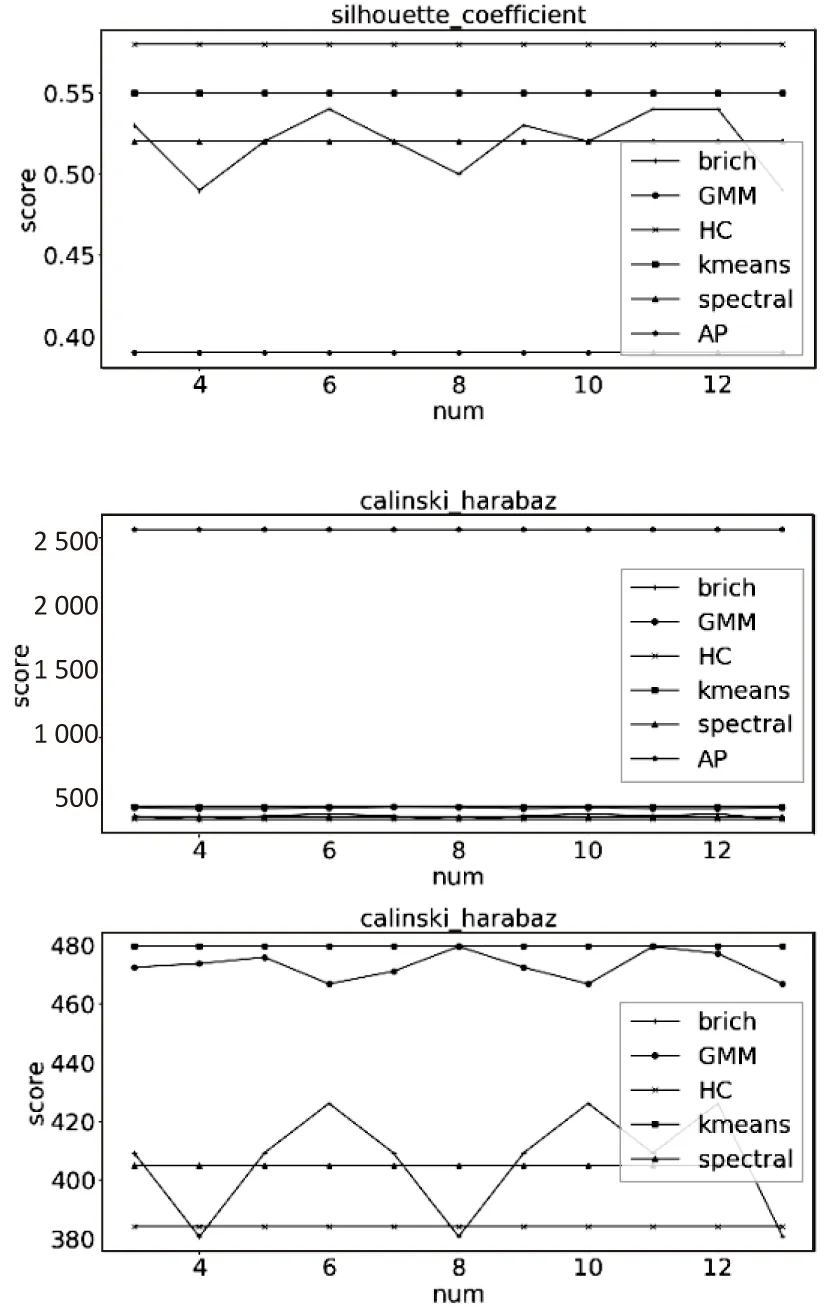
(没有AP算法的局部图)

4.3.3 数据的行数和列数同时增加

当数据集为离散数据时，被测试算法的聚类效果随着行数和列数的增加而变差。从图4(a)中可以看出，当数据集为离散型小数时，算法在两种评价指标下聚类效果很接近，其中Spectral算法的波动性很大。从图4(b)中可以看出，当数据集为离散型整数，在行数超过75时，Spectral算法的CH评分最高；当数据集为连续型正数时，从图4(c)中可以看出，被测试算法的聚类效果在两种评价标准中表现不同。在CH评分下被测试算法聚类效果最好的是AP，其余算法的聚类效果则比较接近，在轮廓系数中当数据集的列数超过4列以后，AP算法的聚类效果最差。

(a)离散型小数

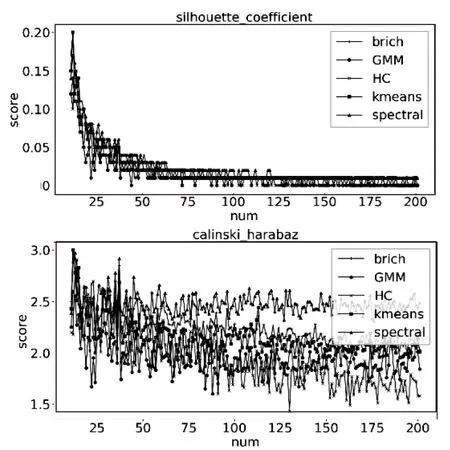
(b)离散型整数

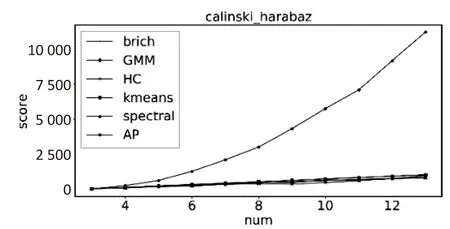
(c)连续型正数

4.4 性能测试

本节在各种数据集上测试了不同算法的消耗时间，以消耗时间的多少作为评价算法效率的标准。本节在离散型小数、离散型整数和连续型正数中分别选取了500行2列的数据集作为研究对象。效果如图5所示。

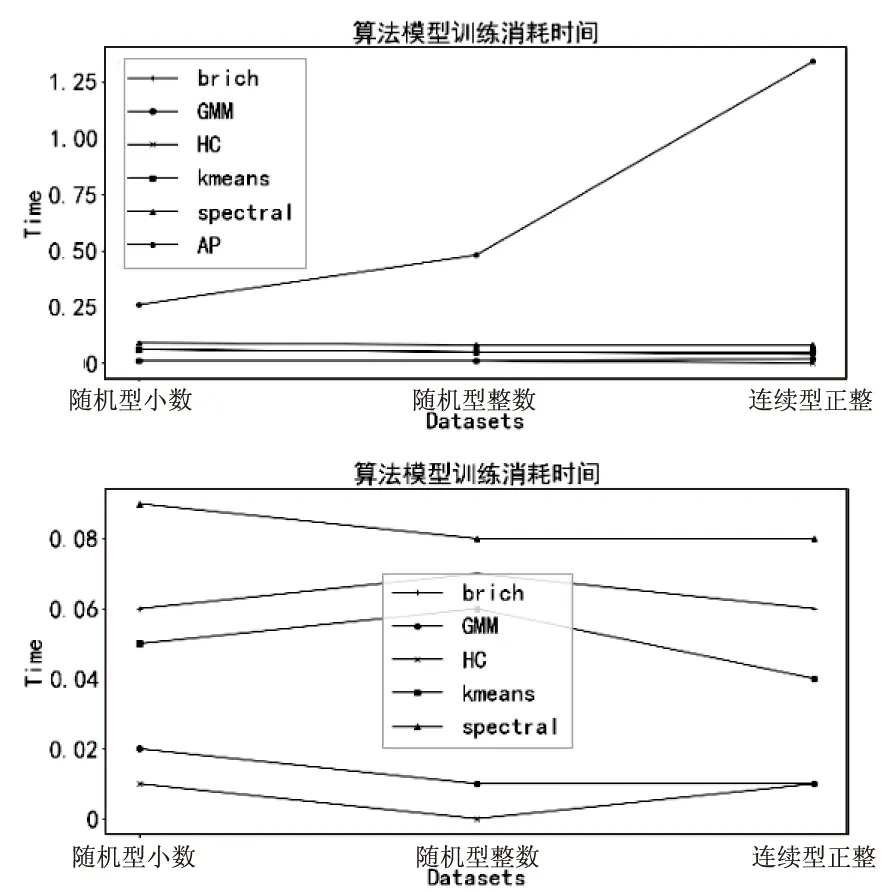
(没有AP算法的局部图)

从图5上图可以看出，AP算法消耗的时间最多，效率最低，这是因为AP算法要提前把数据点的相似度计算出来，加之AP算法的时间复杂度为O(n3)，最后使得AP算法消耗时间最多。AP算法在离散整数型数据集中消耗的时间最少。剩余五种被测试的算法消耗的时间接近，所以特意做了一个没有AP算法的局部图，如图5下所示，其中Spectral算法消耗的时间最多，主要是因为Spectral算法是基于原有数据的相似度来计算特征值，所以花费的时间要多一些。Birch算法在小数中的计算速度最快，是因为其不需要把全部数据遍历完，只需要对叶子节点进行处理，经过多次迭代以后得出聚类中心。因为机器读取小数的速度要快于整数，所以Birch在小数中的效率要更高。K-means、GMM和HC算法在三类数据集中的表现差异不大，说明这三种算法对数据类型的敏感度比较低。

4.5 算法对数据敏感性分析

本节是由不同数量级的数据组成的数据集，由于AP、Birch和GMM算法需要变动参数，所以为了保持全文一致性，没有对这三种算法做敏感性测试。数据集结构为300行2列。横坐标的单位值代表十的一次方，测试结果如图6所示。由图6可知，在两种评价标准下K-means要比其他两种算法的聚类效果好，其中K-means和HC对数量级组成的数据集不敏感，Spectral算法对数量级比较敏感。

图6 算法在不同数量级下的效果对比

5 结束语

通过上述分析，在聚类效果、性能和敏感性三个方面得到以下结论：

(1)聚类效果：①数据只有行数增加时，AP算法和K-means的聚类效果好于其他四种算法；②数据只有列数增加时：在数据类型为离散型小数中，算法的聚类效果很接近，其中Spectral算法的波动性最大。在数据类型为离散型整数中，算法的聚类效果很接近，其中HC算法的波动性最大。在数据类型为连续型正数中，AP算法和K-means的聚类效果好于其他算法；③数据的行数和列数同时增加时：在数据类型为离散小数中，算法的聚类效果很接近，其中Spectral算法的波动性最大。在数据类型为离散整数中，Spectral算法的聚类效果相对好于其他算法。在数据类型为连续型正数中，在CH评分下被测试算法的聚类效果最好的是AP，其余算法效果比较接近，在轮廓系数下当列数超过4以后，AP算法的聚类效果最差。

(2)性能：AP算法消耗的时间最多，效率最低，其次是Spectral算法，剩余几种算法的计算效率比较接近。

(3)敏感性：K-means和HC对数量级不敏感，Spectral算法对数量级相对比较敏感。

综上，在聚类效果、性能和对数量级的敏感性三个方面综合来看，K-means算法相对优于其他五种聚类算法。各个算法各有优缺点：AP算法在连续型正数组成的数据集中，随着行数的增大其聚类效果明显好于其他算法。但是AP算法的效率在六种算法中是最差的；Birch算法的效率在数据类型为小数的数据集中表现最好，但其适用性相对最差；GMM算法聚类效率在连续型正数的数据集中表现的最好；HC和K-means算法的聚类效果在连续型正数组成的数据集中不受列数变动的影响，但在行数变化的离散型数据集中HC算法的聚类效果相对最差；Spectral算法对数据的敏感性相对最高，在小数构成的数据集中聚类效果相对最差。

虽然现在很多聚类算法不断地被提出和改进，但是还没有出现一种适用于不同数据特征的算法，这主要是因为聚类算法没有迭代优化其正确性，而过分强调簇内紧凑，簇间疏离。随着大数据时代的到来，数据不仅越来越多而且数据结构越来越复杂，如何制定一种适合多种情况的聚类算法和评价指标将是下一步需要做的重要工作。