博弈环境下合作达成的策略选择
2020-08-11傅晓岩
傅晓岩
中央财经大学 政府管理学院, 北京 100081
博弈论是现代数学、 运筹学和经济学的交叉理论, 业已形成了较为完整的理论系统。 博弈论(Game Theory) 属于运筹学领域, 是研究具有斗争或竞争性质现象的理论和方法。 博弈论对博弈局中人的选择与行为进行研究, 探讨局中人局势和策略的优化方法。 博弈意味着竞争性的环境, 具有冲突、 竞争与不合作的性质。 但是, 博弈环境与博弈各方合作的存在有一定的关联。 研究博弈环境下合作存在或达成的策略选择将有助于在博弈环境中建构合作, 在竞争决策中寻求最大收益或最小损害。
1 博弈案例与理论
1.1 博弈论的学者
博弈理论是诸多数学家、 经济学家以及计算机方面的专家共同智慧的结晶。 数学家纳什 (John Nash)、 经济学家摩根斯坦(Morgenstern) 与伯特兰(Bertrand)、 计算机方面的专家冯·诺依曼(John von Neumann) 都是博弈理论的研究者。 “1994 年纳什(John Nash)、 豪 尔绍尼 (John Harsanyi)、 泽尔滕(Reinhard Selton), 2005 年奥曼 (Robert Aumann)、谢林(Thomas Schelling) 荣获诺贝尔经济学奖, 以及以博弈论为工具研究信息经济学的米尔利斯(James Mirrlees) 和威克瑞 (William Vickrey), 阿克洛夫(G.Akerlof)、 斯宾塞(M.Spence) 和斯蒂格里茨(J.Stiglitz), 三位学家也在博弈论中做出了突出的贡献, 于1996 年、 2001 年被授予诺贝尔经济学奖”[1]。朱·弗登博格(Dre Fudenberg) 和让·梯若尔(Jean Tirole) 共同撰写的《博弈论》, 更是博弈论理论界的集大成之作。 博弈论是现代学科交叉的产物, 但博弈环境和博弈现象自古就有, 我国古代历史上田忌赛马和空城计就是典型的博弈案例。
1.2 田忌赛马与空城计
“田忌赛马” 的故事, 出自汉代司马迁的 《史记》 卷六十五: 《孙子吴起列传》。 故事讲述战国时期, 大将田忌与国君齐威王赛马, 第一次比赛时, 田忌将赛马按照上、 中、 下三等的顺序比赛, 三战三败输掉了比赛。 在第二次比赛时, 经过孙膑建议, 田忌调整了战术, 用下等马对齐威王的上等马, 用上等马对齐威王的中等马, 用中等马对齐威王的下等马, 最终三局两胜, 顺利赢得了比赛。 在赛马中田忌采纳孙膑建议调整策略, 以自身优势对抗竞争对手之劣势而在竞赛中获胜。 田忌赛马是在竞争环境中以策略对决取胜, 堪称博弈案例的经典。
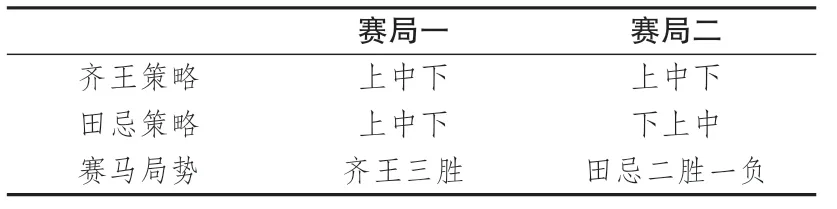
表1 田忌赛马的局势与支付Table 1 The situation and payment of Tian Ji horse racing
“空城计” 则是另外一个出自《三国演义》 的经典博弈事例。 描述的是诸葛亮在马谡失守街亭后, 守卫的西城士兵仅剩2 500 余人, 而司马懿统领精兵15万, 乘胜追击直到诸葛亮退守的西城, 诸葛亮情急之下, 想出“妙计”, 制造假象, 凭栏而坐, 打开城门,抚琴观景, 镇定自若。 司马懿兵临城下, 见此状, 心生疑虑, 暗自退兵。 空城计是一个博弈对局, 博弈双方为诸葛亮和司马懿, 空城计策略对局是诸葛亮空城坚守, 司马懿引兵而回, 留下了武侯弹琴退仲达的知名战例。
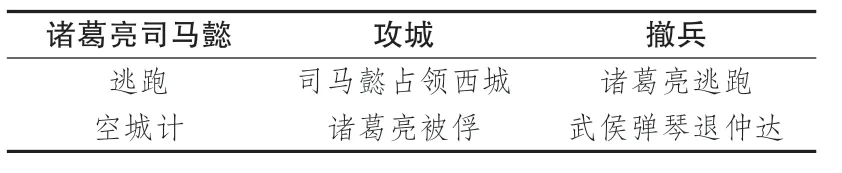
表2 空城计中诸葛亮-司马懿的博弈表Table 2 The game table of Zhuge Liang-Sima Yi in the empty city plan
1.3 现代博弈理论
“田忌赛马” 和“空城计” 是众多博弈案例中的早期典范, 蕴含了博弈论的思想精髓, 印证了博弈双方对峙的竞争环境。 现代博弈论起源于西方, 博弈就是在竞争环境中做出决策的活动, 故亦称对策论。
现代博弈论意指的博弈现象和对局案例应包括四类因素。 一是任何博弈现象或对局都必须包含博弈的局中人, 局中人就是有权自主抉择使用何种策略参与博弈比赛的参与者。 齐威王和田忌是“田忌赛马” 博弈中的局中人; 司马懿和诸葛亮是“空城计” 博弈中的局中人; 大猪和小猪是 “智猪博弈(Pigs’ payoffs) ” 博弈中的局中人; 小朋友是“石头剪刀布”游戏博弈中的局中人。 二是任何发生的博弈事件都一定具备博弈的策略和策略集。 策略是可供局中人选择的实际可行的完整的行动方案, 从而策略的全部集合构成了策略集。 在剪刀石头布游戏中, 剪刀、 石头、布都是博弈策略, 而剪刀、 石头、 布三个策略共同构成游戏博弈的策略集。 策略集包含的策略可以是有限集, 也可以是无限集。 如果在一个博弈中局中人总共有有限个策略, 则称为“有限博弈”, 反之称为“无限博弈”。 “田忌赛马、 空城计、 剪刀石头布、 智猪博弈(Pigs’ payoffs) ” 均为有限博弈。 三是任何博弈现象必当发生局势与支付函数。 局中人从各自策略集中取一种策略组成的策略对局称为局势, 每一策略对局的得失或结果称为局势, 也是局中人的支付函数,亦称赢得。 四是现代博弈论的重要基础和先决条件:博弈局中人信息掌握的对称性、 完整性。 博弈局中人既知道自己和对方的博益策略与赢得, 同时每个博弈局中人也必须知道其他局中人也掌握这些信息。
1.4 博弈类型与纳什均衡
博弈论是诸多学科学者集体智慧的结晶, 博弈论研究分支众多, 研究成果异常丰富。 依据当前博弈理论研究成果, 可按三个标准对博弈进行分类。 “按博弈局中人是否合作, 博弈分为非合作博弈与合作博弈”[2]按局中人博弈结果总和是否为零, 分为零和博弈、 非零和博弈; 按策略集中的策略项目的有限和无限, 分为有限博弈与无限博弈。 现实中的博弈, 往往是非合作博弈, 甚至为零和博弈, 博弈往往会导致竞争、 冲突, 常引发困境与悲剧的发生。
博弈中的困境与悲剧比合作与共赢更容易发生,且困境与悲剧总是以纳什均衡(Nash Equilibrium) 局势出现。 “纳什均衡指的是这样一种策略组合, 在该策略组合中, 由所有人的最优策略组成。”[3]参与人单独改变策略都不会得到任何好处。 即如果在一个策略组合中, 所有参与人都不改变策略, 没有人会改变自己的策略, 则该策略组合就是一个纳什均衡。 然而,诸多的纳什均衡并不意味着合作与双赢, 而恰恰意味着困境与悲剧。
2 博弈环境下的困境与悲剧
博弈意味着竞争, 竞争往往意味着非合作, 在非合作情况下往往衍生出诸多的困境与悲剧, 著名的博弈案例还有诸如囚徒困境(Prisoner' s Dilemma)、 公地悲剧(Tragedy of the Commons) 等。
2.1 囚徒困境
“囚徒困境” 是1950 年美国Rand 公司顾问艾伯特·塔克(Albert Tucker) 提出的博弈论模型。 囚徒困境案例讲的是两个共谋犯罪的嫌疑犯被警察抓住关进监狱的不同房间进行审讯而不能互通消息。 如果两个人都不揭发对方, 则由于缺乏足够证据, 每个人坐牢1 年; 如果两人中一个人抵赖而另一个人坦白, 坦白者因坦白从宽揭发立功而即可获释(0 年), 抵赖者因抗拒从严而加重责罚判刑10 年; 如果两人无法信任对方, 倾向于互相揭发, 而不是同守沉默, 则因证据确凿各判刑坐牢8 年。 警方对两个囚徒犯罪事实的认定, 取决于两个囚徒自行选择的策略: 是否供认。
如表3 囚徒困境的支付矩阵, 在囚徒B 坦白的情况下, 囚徒A 的最优策略是坦白, 只有这样才能不被对方出卖, 如果抵赖将会被判刑10 年, 坦白比抵赖占优; 在囚徒B 抵赖的情况下, 囚徒A 的最优策略也是坦白, 这样自己就可以即可获释出狱了, 如果抵赖将会被判刑8 年, 坦白比抵赖占优。 总之, 无论囚徒B 供认与否, 囚徒A 的占优策略是选择“坦白”, 同理, 囚徒B 的占优策略也是选择“坦白”。 无论对方是否选择“坦白”, 自己选择“坦白” 的结果要优于选择“抵赖” 的结果, 最好的结果是 (坦白, 坦白), 最终形成“囚徒困境” 的中纳什均衡。

表3 囚徒困境支付矩阵Table 3 Prisoner' s dilemma payment matrix
两个理性人总会试图将自己受到的惩罚降到最低, 因而囚徒A、 B 总会选择坦白而不是合作起来抵赖, 这对于自己来说是最好的策略。 但是由于囚徒A、 B 都理性的选择了不合作的坦白, 导致两人都受到了8 年牢狱之灾, 共计16 年, 远远大于两人合作抵赖和一方抵赖一方坦白, 即表1 支付矩阵中的2R>S+T>2P, 个体的理性造成了集体的悲剧, 陷入了困境。
2.2 公地悲剧
如同“囚徒困境”, “公地悲剧” 的发生, 是个体的理性造成了集体的悲剧。 公地悲剧理论, 是英国加勒特·哈丁(Garrett Hardin) 教授在《The Tragedy of the Commons》 文中首次提出来的博弈理论模型,随后即被制度经济学广泛引用。 加勒特·哈丁(Garrett Hardin) 教授借用牧羊者使用可以自由放牧的公用地, 阐释“集体资源的使用会毁灭整个集体资源”的论点。
哈丁教授指出, 自由放牧的牧羊者都是理性人,都希望自己能够足够放牧更多的牲畜。 但是牧场还存在其他牧民, 他们也希望放牧足够多的牲畜。 牧民知道自己不多增加牲畜, 其他牧民也会增加牲畜, 牧民几经思考的结论必然是自己要增加牲畜, 于是牧民无视草地承载力而增加牲畜。 其他牧民不会因为有牧民增加牲畜而减少自己的牲畜以保护草场, 而是见到有利可图纷纷增加自己畜牧数量。 牧民不顾草地承载力纷纷增加畜牧量, 必然导致草地恶化最终无法放牧,最终引发“公地悲剧”。
个体理性造成了集体困境, 竞争环境(博弈) 中的不合作再次导致了悲剧, 以至于哈丁做出了“公共资源的自由使用会毁灭所有的公共资源”[4]的论断。
“公地悲剧” 中牧民无节制的放牧原理, 同样可以用于现代海洋典型的捕捞问题, 渔业资源如同草地, 属于公共资源, 任何拥有渔具的渔民都可以进行捕捞, 而不为其他渔民所获, 但是渔业资源是稀缺的, 过度捕捞会导致渔业种类的资源量下降和海洋资源的整体衰退, 从而对渔民后代的利益造成损害, 生态链的环环相扣, 持续下去造成对海洋资源不可逆转的破坏, 这就是现代的“资源枯竭型公地悲剧”[5]。
2.3 如何避免困境与悲剧
从囚徒困境和公地悲剧中可以看出, 博弈环境下由于不合作往往会产生困境和悲剧, 那么如何改变不合作而避免困境与悲剧的发生呢。
理性人从事任何经济活动时都是利己的, 都会为自己的利益最大化寻求相应的最优策略。 任何人都有人性的弱点, 人不是天使, 都往往首先关心自己的利益。 在每个人都有自私动机情况下, 怎样才能在彼此竞争的博弈环境中构造合作成为了一个难题。 但合作的构造是避免博弈中悲剧发生的关键环节, 因此博弈环境下达成合作的策略成为了一个非常值得探讨的问题。
3 博弈环境下达成合作的策略
博弈环境之中难道没有合作的情况吗? 答案是否定的。 我们可以从这些案例中探寻博弈环境中合作达成的原因, 进而促进合作进化, 避免悲剧和困境的产生。
3.1 博弈环境下的合作
谈到博弈环境下, 弱肉强食的生物界中的共生合作以及残酷厮杀战场的堑壕默契应当值得关注。
3.1.1 生物界的共生
生物界历来遵循弱肉强食的“丛林法则”, 大自然中各种生物也是以物竞天择和适者生存为基础的, 相互的生存冲突造成了物种间的博弈, 生物进化论也由此而来。 与此同时, 生物界也出现了“共生现象”, 在这里共生往往被看成一种适应现象。 真菌和藻类共同生成了地衣互补养料; 无花果的花朵是黄蜂的寄居地,而黄蜂传播无花果的花粉以及小丑鱼和海葵的互利共生。 生物界的共生现象对于博弈环境中寻求合作策略有着深远性的启示。 生物共生关系的发生往往是生物之间彼此能够互惠, 换言之, 生物共生是建立在回报基础上的, 而回报更是博弈环境中合作建立的基础。
3.1.2 敌对堑壕的默契
对于生物界有基于互惠而产生共生的合作现象,在人类最残酷的战争中也有合作的发生。 战争的双方是处在最激烈的博弈环境之中, 存在着你死我活的冲突, 这是合作最不可能发生的地方, 但是这里仍然存在默契的合作。
在一战期间, 西部战场形成了为领土而疯狂厮杀的残酷场面, 但在这些残酷战役的空隙在法国和比利时长达五百里的战线对峙中, 敌对士兵出现了极大的克制与默契。 战争双方强烈对抗情况下还能出现合作情况, 这种“自己活也让别人活”[6]系统成因何在。 对于战争任何一方, 杀伤对方削弱敌人都是必要的, 杀伤对方等于保护自己, 但是杀伤对方总会招致敌军的报复。 虽然司令部强调进攻锐气,要求进攻和射击敌人, 但是英军射击德军, 总会遭遇德军的报复性炮击, 反之亦如此。 堑壕战中彼此长时间对峙, 使得敌对双方能够频繁接触, 告诉对方自己愿意保持默契让彼此休息、 吃饭以及伤亡救助和运送物资, 也告诉对方自己能够报复如果有必要的话。 在堑壕战中, 克制不是因为软弱, 而背叛只能带来自我伤害, 显然双方克制比彼此惩罚好,于是在强烈敌对状态下合作便形成了。 可见, 回报是合作的基础, 并且合作需要善良的对待和背叛的反击, 并且需要长期反复来加强。
3.2 博弈合作的策略达成
合作能够在丛林法则中生存, 合作能够在堑壕厮杀中保持, 博弈环境下合作策略达成成为现实。
3.2.1 重复囚徒困境的比赛
对于博弈环境下合作策略逐渐刻画出来, 其实阿克塞尔罗德在“重复囚徒困境” 的计算机比赛中让合作的策略更加成熟。 在众多的计算机程序中, “一报还一报” 在两次比赛中保持领先, 但是“一报还一报” 在大多单次比赛中并不占优势。 “一报还一报”是一个善良的策略, 非常简单, 首先选择不背叛, 选择合作, 再按照对方上一步的决定而做出相应的选择。 “一报还一报” 策略的可能性是显而易见的, 具有善良特征, 因为一开始选择合作而非背叛; 具有报复特征, 因为对方一旦背叛就会遭到报复; 具有包容特征, 因为对方停止背叛、 选择合作将会出现合作回归; 具有清晰特征, 因为对方很快就能知道自己合作对方也会合作, 自己背叛对方立刻背叛。 合作策略在“一报还一报” 策略中形成了自己的清晰构架。
3.2.2 合作存在与达成的策略
基于上面探讨, 博弈环境下合作达成的策略选择已经明确。
合作必须基于回报。 亲友之间的背叛也会出现, 亲缘和信任不是合作的必要条件, 合作是利益最大化的博弈结果。 例如我们会思考, 还要不要邀请从来不回请我们的朋友来就餐。 我们在博弈环境下, 冲突倾向比较强烈, 加大合作的回报将会是避免冲突的有效选择。
合作应当基于重复。 生物的共生、 堑壕的默契、囚徒困境的避免, 都具有重复博弈性质。 重复是相对单次博弈而言, 是区别于今后不会再遇见而所言的。单次博弈的囚徒困境, 因为人性自利, 一般会选择背叛, 这也是人之常情。 自己家楼下的食品摊位, 往往允许赊账并且从来都是物美价廉而足斤足量, 而火车站的商贩总是缺斤少两并且价格昂贵宰客行为频发,原因就在于一个是重复性合作, 一个是一次性买卖。
合作需要善良本性。 “一报还一报” 策略能够破解“囚徒困境”, 带来合作。 在重复囚徒困境的程序比赛中, 善良的本性能够把程序按照得分高低区分开。 “一报还一报” 策略因为不首先选择背叛, 所以有明显的善良特征。 善良的人有恻隐之心, 不会无缘无故伤害别人, 这样就减少了博弈冲突的激化而增进了博弈之中合作的可行性。
合作要求可激怒性。 “一报还一报” 策略之所以能够成功, 还在于其对合作与背叛都给予对等的回报。 对合作给予合作, 对于背叛行为给予还击, 合作的可激怒性, 防止了试探性背叛的“检验者” 和“镇定者”。 合作是建立在对等前提之下的, 对于背叛者的容忍将会助长背叛者的嚣张气焰, 对于背叛行为要坚决的抵制和打击。 古希腊故事中讲述: 牧羊人古格斯品行低劣, 无意间得到了一枚可以隐身的戒指, 当他知晓戒指可以隐身后, 利用戒指引诱王后, 谋杀了国王最终还窃取了王位。 这印证了“一个人即使日常平中奉公守法、 循规蹈矩, 但行为一旦不受约束, 就会做思想中想做的事情, 而不是应该做的事情”, 因为隐身戒指使其为所欲为不会受到惩罚。 惩罚的必要性可想而知, 不仅可以打击坏人的入侵还可以避免好人被纵容成坏人。 由此可见, 在由利己主义者组成的社会关系中, 可激怒性是合作的持续保障。
合作不可或缺宽容。 “一报还一报” 策略对于背叛给予坚决的反击, 但对于曾经背叛的程序一旦采取合作就会报之以合作, 体现了宽容性。 宽容性区别于某些一经遭遇背叛便从不合作的程序, 合作一经破裂将再无弥合机会。 博弈环境中的冲突难免发生, 不能因为曾经冲突过而坚决不合作, 毕竟金无足赤, 要原谅别人的过失。 宽容能够增强合作关系的可持续性。
合作策略应当清晰化。 合作策略的清晰性, 即告知博弈环境中的局中人对合作与背叛都会给予相应回报, 更加重要。 最佳的合作模式是对合作要给予回报, 对背叛也要给予还击, 是合作基础。 合作策略的清晰性可以避免博弈局中人背叛的企图和尝试, 把不合作扼杀在萌芽状态。
举例来看, 如“共享单车” 作为新兴的事物, 以方便快捷低廉进入大众视野, 解决了诸多出行者“最后一公里” 的问题, 但追求过快的用户数量, 不计成本的快速扩张, 也带来诸多问题。 由此, 应建立共享单车平台与政府监管战略选择的博弈策略, 政府出台全面有效的行政法规进行规范管理与惩罚措施, 对平台加以合理的引导和规范, 对共享单车适当把控, 同时通过多媒体等方式加大舆论宣传力度, 建立公民诚信管理机制, 从源头提高社会公众对公共社会资源的认知度, 最终建立起共享经济政府下的共享经济生态平衡[7]。
综上, 合作策略具有回报性、 重复性、 良善性、 可激怒性、 宽容性以及清晰性, 将改变博弈之中的纳什均衡, 从原来的(背叛, 背叛) 变为(合作, 合作) 的纳什均衡。 让博弈环境中的局中人从合作中获利, 让任何局中人没有积极性采取其他的策略, 合作是其最佳选择。
注释:
① 田忌赛马处于非对称信息状态,属博弈案例但区别于现代博弈理论 信息完整要求。
