下覆基岩断层对边坡稳定性的影响分析
2020-08-11窦思军徐兴倩李继国和春香
窦思军, 徐兴倩, 李继国, 和春香, 焦 萱
1.云南农业大学 水利学院, 云南 昆明 650201; 2.云南水利水电职业学院, 云南 昆明 650201
0 引言
近年来, 由于断层地质构造引发的滑坡地质灾害给人类生产、 生活造成巨大损失。 如湖南省安化县因断层引发崩塌、 滑坡等地质灾害点多达57 处, 造成89 人死亡, 多条交通主干线受损, 直接经济损失近5 692万元[1]。 断层影响露天矿的生产安全, 内蒙平庄西露天煤矿、 辽宁弓长岭露天铁矿、 新疆黑山露天铁矿等因断层存在而诱发滑坡地质灾害给矿区人民的生命财产安全造成严重威胁[2]。 由上述案例可见, 断层对边坡稳定性有重要影响。
当前, 国内不少学者对断层引发的滑坡案例进行相应研究。 曹兰柱等[3]运用3Dslop 软件对存在斜交断层的某露天矿滑坡进行三维数值模拟研究, 探讨其滑坡失稳破坏模式及形成机理; 李万逵等[4]对新疆某水利工程坝址右岸高边坡稳定性进行现场勘查和综合分析, 明确指出断层对该边坡的稳定性有显著影响; 黄润秋等[5-7]研究“汶川地震” 后形成的断裂构造, 对断裂构造与滑坡的相关性进行系统分析; 刘宏力等[8]通过研究某高速路边坡断层破碎带的物理力学特征,分析其对边坡稳定性的影响; 许益东等[9]运用有限元法建立边坡三维模型, 讨论了顺层边坡岩层倾角与边坡稳定性的关系; 何大钊等[10]通过室内实验探讨断层破碎带土体的泊松比、 内聚力和内摩擦角等力学参数取值对边坡稳定性的影响。 然而, 学者研究断层控制的滑坡现象主要集中在断层类型、 断层破碎带等要素之上, 分析下覆基岩断层对边坡稳定性影响的案例较少, 需进一步深入研究。
论文以云南省昌宁县河西水库滑坡为研究对象,采用ANSYS 有限元软件建立下覆基岩断层边坡数值模型, 模拟不同位置倾角的下覆基岩平移断层、 正断层、 逆断层, 改变平移断层的位置, 计算不同条件下边坡稳定安全系数, 分析下覆基岩断层对边坡稳定性的影响, 为研究下覆基岩断层诱发滑坡提供理论参考依据。
1 工程概况
河西水库滑坡位于云南省保山市昌宁县田园镇境内, 距昌宁县城9 km。 该区地处横断山脉南段, 滇西纵谷西南部, 昌宁盆地北东缘, 属侵蚀构造地形中山陡坡型地貌。 坝址以下河道向南流入昌宁盆地, 呈蛇曲状, 纵坡相对较缓, 山谷较开阔, 两岸斜坡为台阶型。 库区地下有弱含水地层, 出露厚度较小。 受地形地貌、 下伏地层完整性、 地下水储存条件的影响, 库区地层为富水性弱或不含水地层。 库区岩层总体产状倾向于北东和北西, 倾角在6°~45°之间, 断层两侧倾角变化较大, 在20°~70°之间。 岩层产状变化较大, 局部褶曲发育, 两组褶曲呈共轭“X” 型的压扭性构造裂隙。 由于水库处于断裂挤压破碎带上, 左坝肩边坡上已出现滑坡现象, 形状为两条近东西走向冲沟挟持的宽缓山脊地带。 滑动面位于片岩内, 为顺层滑动。 滑坡已产生明显变形, 变形特征主要表现为:挡墙开裂变形、 地面沉陷、 滑坡后部小路内侧出现边沟、 溢洪道和溢洪闸变形等, 滑坡典型工程地质剖面如图1 所示。
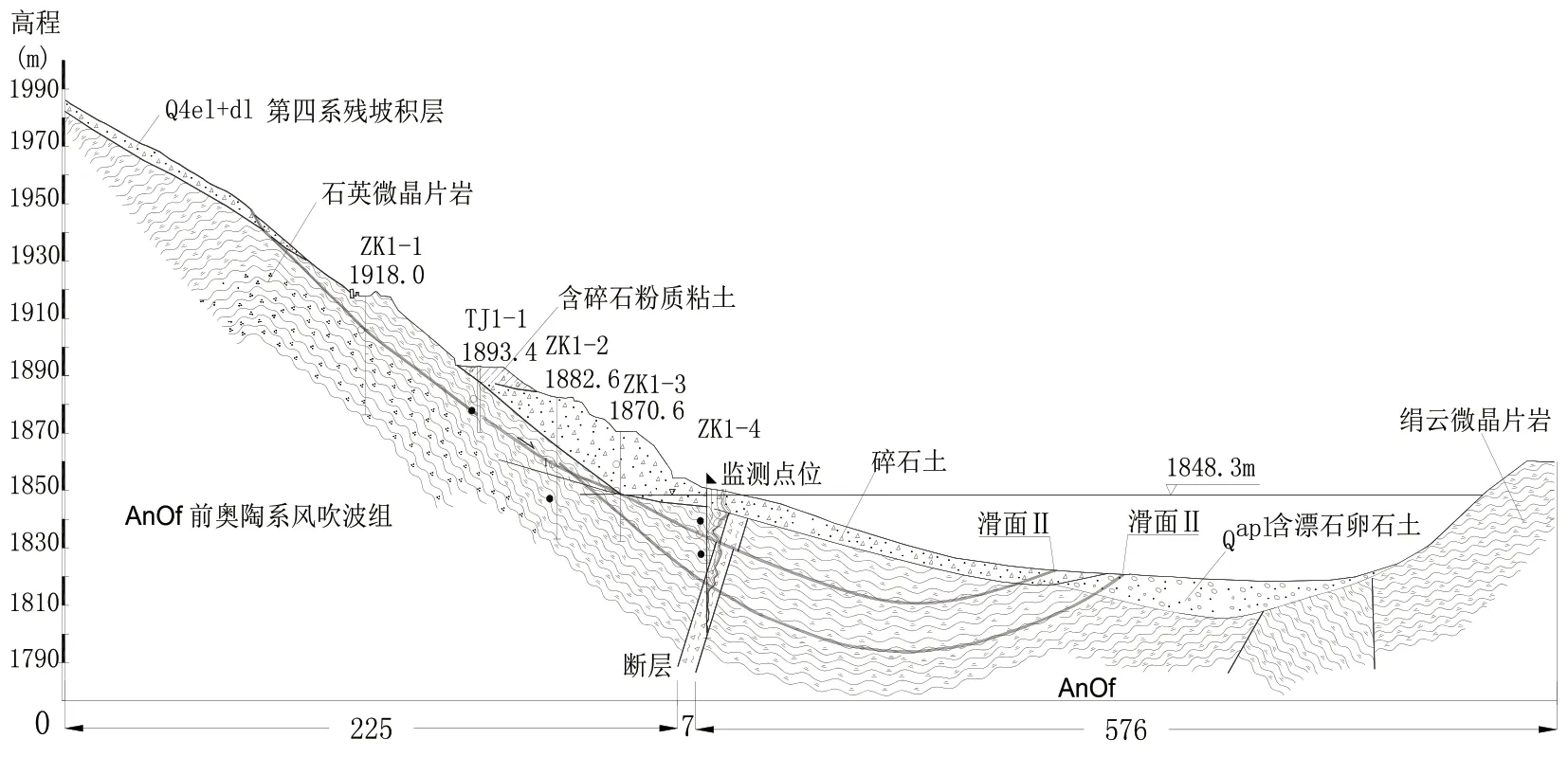
图1 滑坡工程地质剖面图Fig.1 Landslide engineering geological profile
2 研究方法
2.1 滑坡工程地质模型
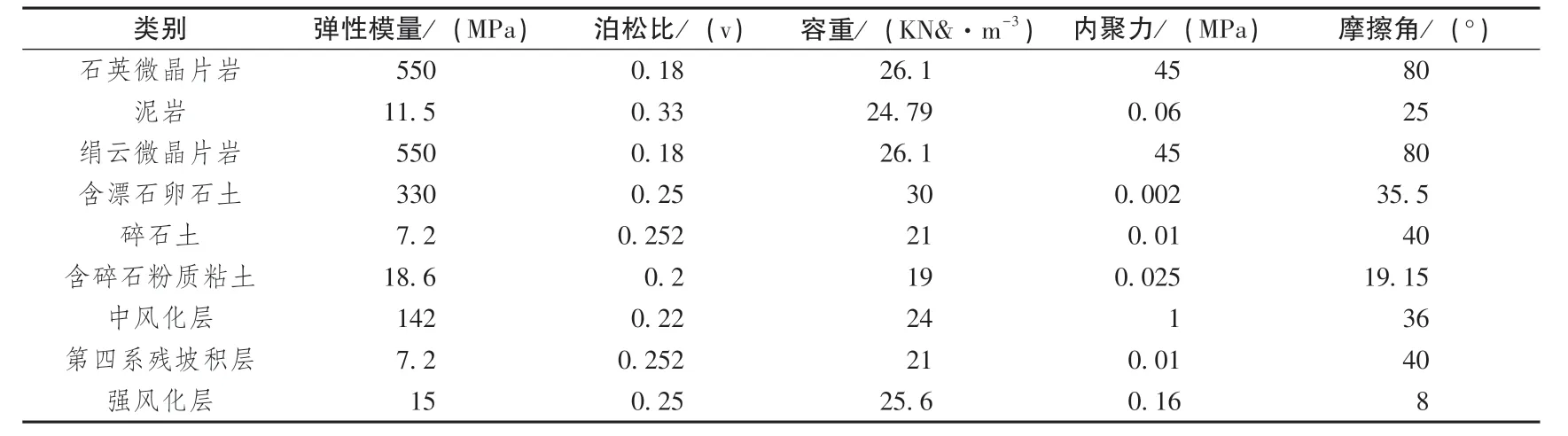
表1 边坡各层岩土体参数表Table 1 Parameters of rock and soil mass
2.2 滑坡数值计算模型
滑坡模型按平面应变问题考虑, 在ANSYS 中构建等面积的D-P 模型, 模型中的岩体按理想弹塑性材料处理。 计算单元选取适合弹塑性分析的PLANE82等参单元, 单元有8 个节点, 16 个自由度。 对模型边界条件设置法向约束X, 底部施加竖向约束Y, 滑面边界无约束可自由滑动。 边坡模型整体自由划分为9 548 个非结构型网格, 网格划分如图2 所示。
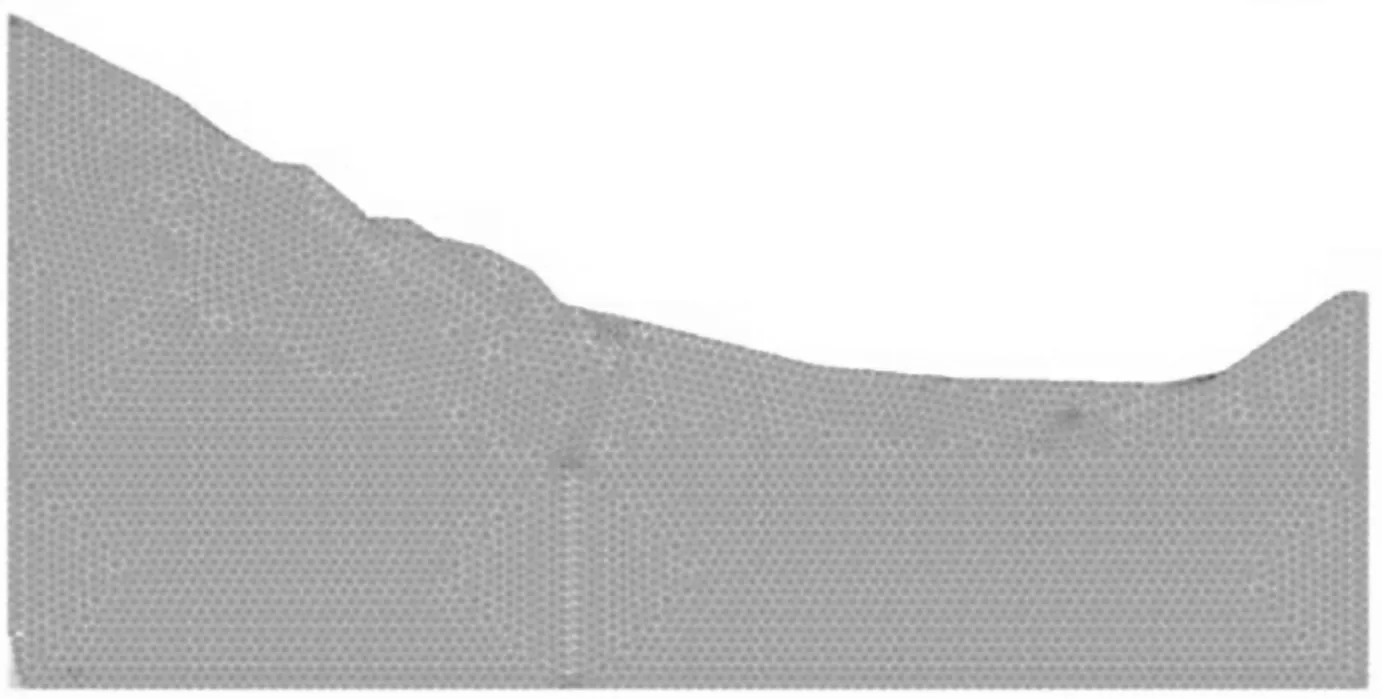
图2 边坡有限元网格划分Fig.2 Finite element mesh generation of slope
2.3 强度折减法原理
采用强度折减法计算边坡稳定安全系数[11,12]。 首先选取初始强度折减系数F, 然后将边坡岩体材料内聚力c 和内摩擦角φ 同时除于初始强度折减系数F,折减后土体内聚力c′及内摩擦角φ′分别为:

不断改变强度折减系数F, 将折减后的c′和φ′输入到ANSYS 等面积D-P 本构方程中进行重复迭代,根据迭代程序的收敛性判断边坡是否趋于稳定。 若程序收敛, 则边坡不稳定, 继续增大强度折减系数F,直到程序恰好不收敛, 此时的强度折减系数即为边坡稳定安全系数FS。
广义判定边坡是否发生失稳破坏的依据有: (1)塑性区贯通判据, 根据某一幅值的广义塑性应变或等效塑性应变自坡脚下方向坡顶上方是否贯通作为边坡失稳破坏的标志。 (2) 位移突变判据, 边坡的破坏常常伴随着位移较大的变化, 因此可以根据计算区域内某一部位或某点的位移是否发生突变作为边坡是否发生失稳破坏的判断依据。 (3) 计算程序收敛性判据,将折减后的c′和φ′输入到ANSYS 有限元软件中进行计算, 若计算程序一直趋于收敛, 则边坡处于稳定状态, 当程序发生恰好发生不收敛时, 边坡将发生失稳。
3 边坡稳定性分析
以下覆基岩平移断层为例, 建立不同倾角和不同位置条件下的边坡模型, 通过强度折减法计算边坡稳定安全系数FS。 相同条件下, 对比平移断层、 正断层、 逆断层的塑性应变云图和沿x 方向的位移云图,总结归纳不同下覆基岩断层类型及位置对边坡稳定性的影响规律。
3.1 不同倾角平移断层对边坡稳定性的影响分析
将平移断层倾角设计为15°、 30°、 50°、 72° (真实断层倾角)、 100°、 120°六个方案, 通过迭代程序的收敛性, 将各个方案下边坡的稳定安全系数FS计算结果列入表2 中, 结合不同角度下边坡塑性应变云图和沿X 方向位移云图(图3) 分析断层倾角对边坡稳定性的影响。

表2 不同断层倾角对应的边坡安全系数Table 2 Slope safety factor corresponding to different fault dip angles
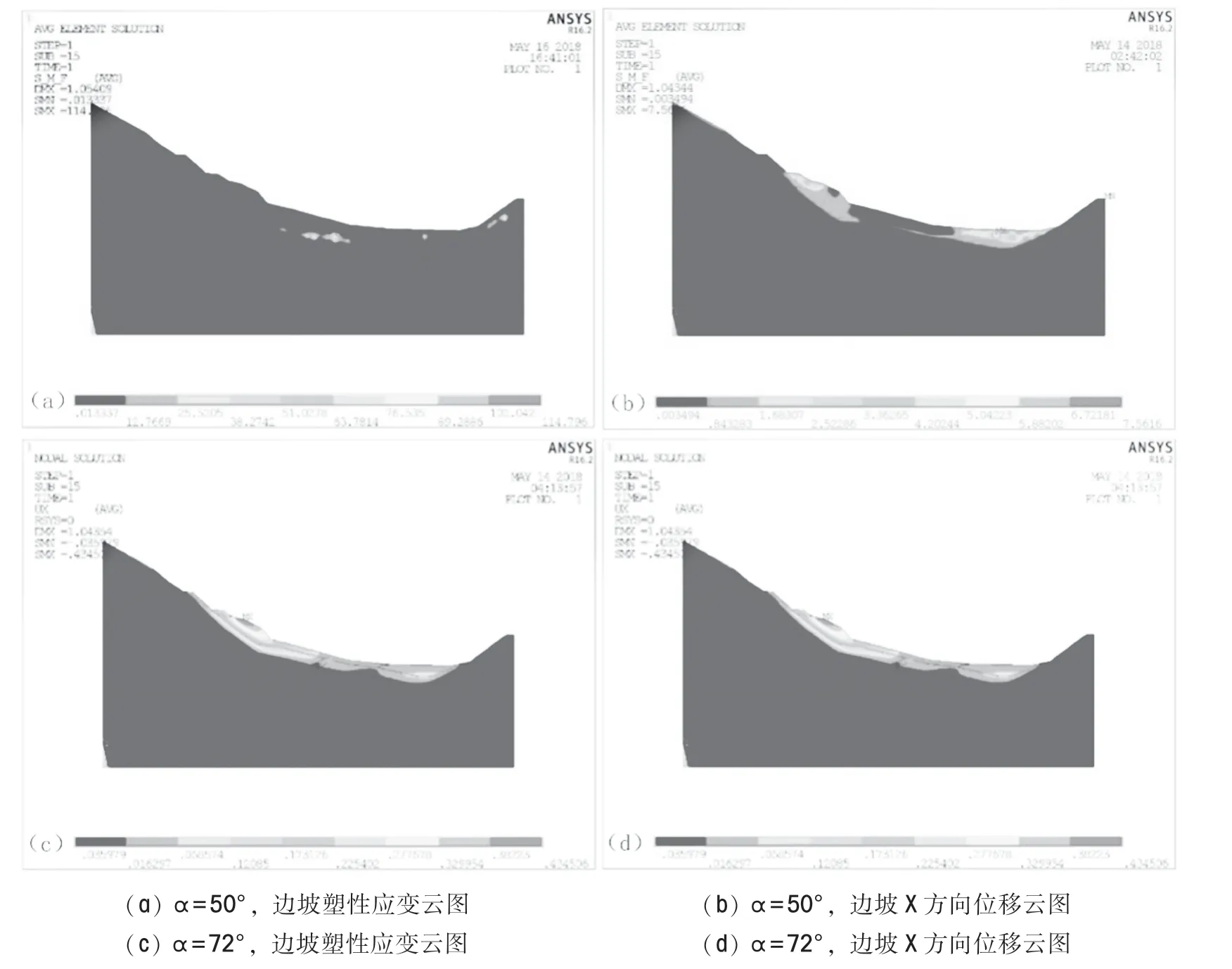
图3 不同角度下边坡塑性应变云图和沿X 方向位移云图Fig.3 Plastic strain nephogram and X-direction displacement nephogram of slope at different angles
断层倾角为15°和30°时, 边坡模型中未发生塑性应变。 当断层倾角从30°增大到50°时, 从图3 中(a)图可以清晰地看出在边坡坡脚处和水库底层出现了小范围的塑性应变区域, 并且有逐步发展的趋势, 若继续增大断层倾角至72°, 此时边坡下部和水库底层出现更大范围的塑性应变区域, 两者内部出现了一条塑性带, 该塑性带从水库底层开始, 逐步向坡顶有完全贯通的趋势, 如图3 中(b) 图所示。 对比边坡沿X 方向的位移云图可知, 断层倾角从50°增大到72°的过程中,边坡出现的塑性应变区域从无到有, 从小面积到大面积有逐步贯通的趋势。 当断层倾角达到72°时, 在坡肩处出现了明显的滑移现象, 如图3 中(d) 图所示。 以上综合迹象表明边坡的整体稳定性发生了改变, 根据计算步骤和边坡失稳判据, 当强度折减系数F =1.03时, 计算程序在此时恰好发生不收敛, 因此可认为本实例边坡的稳定安全系数Fs 为1.03。
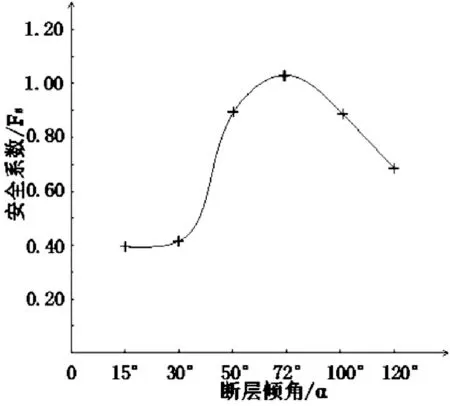
图4 边坡安全系数随平移断层倾角变化曲线图Fig.4 Curve of slope safety factor with dip angle of translational fault
图4 所示为下覆基岩平移断层边坡稳定安全系数随断层倾角的变化关系图, 由图可知断层倾角从15°增大到120°的过程中, 边坡稳定安全系数Fs 呈现先增加后减小的趋势。 当断层倾角为72°时, 此时边坡稳定安全系数达到最大值1.03。 根据边坡的塑性应变云图可知, 在坡脚和坡肩之间出现一条几乎完全贯通的塑性带, 此时边坡已进入塑流状态。 基于强度折减法原理, 可判定此时边坡达到极限平衡状态, 即将发生失稳破坏。 继续增大断层倾角, 坡体内部区域产生不同程度的塑性应变区域, 但塑性应变区域始终未发生贯通, 边坡稳定安全系数随之不断减小, 但边坡始终处于稳定状态。
3.2 不同位置平移断层对边坡稳定性的影响分析
根据平移断层在边坡中所处位置, 设计断层距离原点x =125 m、 175 m、 225 m、 275 m、 325 m、375 m、∞处(无断层处) 六个模拟方案, 基于强度折减法原理, 计算对应条件下的边坡稳定安全系数如表3。
通过对比分析各模型方案下的塑性应变云图可知, 当平移断层距离边坡原点小于225 m 时, 无论增大或减小强度折减系数, 边坡均未出现塑性应变区域, 且计算程序一直未发生收敛。 继续改变其强度折减系数, 当强度折减系数F 为1.03, 断层距离原点为225 m 时, 程序恰好出现不收敛的现象, 结合判定原理可认为边坡的稳定安全系数为1.03。 继续改变断层距离原点的位置时, 边坡的稳定安全系数不再发生变化, 所以判定此种工况条件下, 边坡趋于稳定状态。

表3 平移断层不同位置距离原点的边坡安全系数表Table 3 Safety factor table for different locations of translation faults on slope
3.3 下覆正断层和逆断层对边坡稳定性的影响分析
根据平移断层不同倾角、 不同位置条件下边坡稳定安全系数的分析结果, 按照相同的建模方法, 构建正断层、 逆断层边坡模型。 结合不同类型边坡的塑性应变云图、 边坡沿x 方向位移云图, 总结不同类型断层对边坡稳定性的影响规律。
根据下覆正断层边坡模型塑性应变云图可知无论是增大或减小强度折减系数, 边坡模型的塑性应变区域始终未发生贯通, 且沿X 方向的位移变化始终很小, 可忽略不计。 相比之下, 逆断层边坡模型在水库底层和坡肩处各自出现了小范围的塑性贯通区域, 说明该位置处边坡的稳定性发生了变化。 图5 和图6 分别示意正断层、 逆断层边坡沿X 方向的位移云图, 通过对比可知逆断层坡体变形加剧, 且在坡肩围岩处出现的位移比正断层大, 说明正断层对滑坡的发生起到一定的阻挡作用, 而逆断层有加剧滑坡发生的趋势。
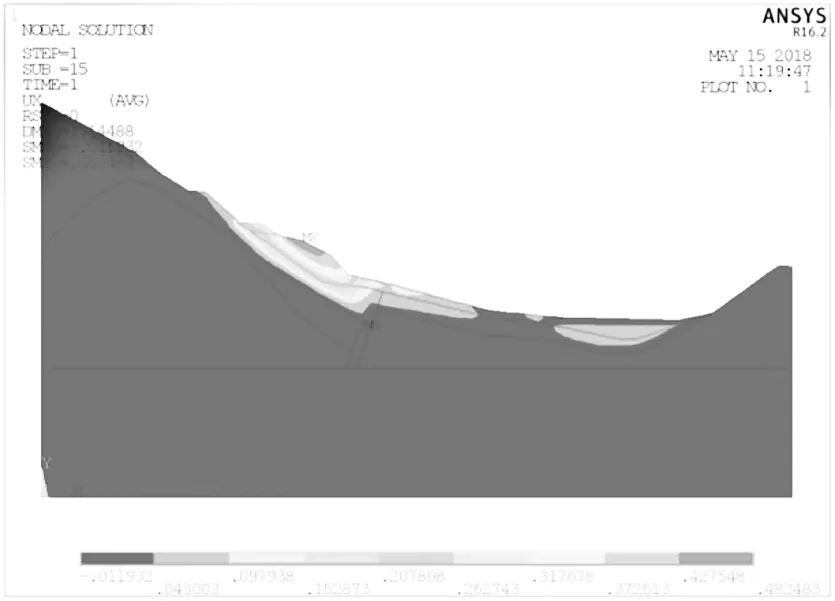
图5 正断层α=72°, 边坡x 方向位移云图Fig.5 Normal fault of α= 72 °, x direction of slope displacement nephogram

图6 逆断层α=72°, 边坡x 方向位移云图Fig.6 Thrust of α= 72 °, x direction of slope displacement nephogram
4 结语
论文以河西水库边坡下覆基岩断层为例, 以不同断层要素为研究变量, 采用ANSYS 数值模拟软件分析不同条件下边坡的稳定性, 通过对比分析得出以下几个结论:
(1) 当下覆基岩断层为平移断层时, 断层倾角小于72°, 边坡稳定安全系数随断层倾角的增大而增大,当断层倾角大于72°, 边坡稳定性安全系数逐渐降低。
(2) 当下覆基岩为平移断层时, 在断层位置距离原点一定范围内, 边坡安全稳定系数随断层离原点的增大而增大, 当断层位置达到一定的距离后, 边坡的稳定性系数不在发生变化, 断层位置对边坡稳定性的影响作用不是特别明显。
(3) 在相同条件下, 相比平移断层, 下覆正断层对滑坡的孕育有抑制作用, 而逆断层对滑坡的发生有促进作用。
