基于支持向量机技术的测量粗差剔除方法研究

李木子 李 华*

（1、长春市市政工程设计研究院，吉林 长春130041 2、吉林建筑大学交通科学与工程学院，吉林 长春130118）

在实际测量中，测得的数据不可避免的会含有粗差，如果粗差不剔除，在其干扰下测量结果就会产生偏倚甚至被歪曲，对施工质量和工程进度造成极其严重的影响。为了保证平差的准确性和测量数据的高精度，在进行测量数据平差之前应该对观测值进行检测，检验出含有粗差和系统误差的观测值并将其剔除。

粗差对平差结果乃至整个工程项目都会造成严重的后果和恶劣影响，测量工作者一直致力于探索合适的方法检测粗差并将其剔除[1]。根据概率统计原理，当母体基于随机变量时，其应该严格服从某一特定分布模式这一假设。而粗差的存在则破坏了这一基本假设，即，由于粗差的存在平差后，平差结果将会出现错误估计。近代测量学和统计学的专家学者针对粗差问题，提出一种名为污染误差的模型，将误差模型从经典的偶然误差范围扩展到了粗差的范围，各种粗差的检测和处理方法相继被提了出来，形成了粗差的统计诊断理论[2]。经过相关领域学者的进一步研究，总体可分为两类的多种抵抗粗差干扰的方法被提了出来，分别是：基于假设检验的粗差探测、辨识和修正的方法；在数学领域中称为抗差估计的方法，或称稳健估计。关于粗差定位与剔除的研究仍在不断地探索之中，它是关乎理论和算法的问题。其中，关于不同平差系统以及可能出现的多种类型的粗差，对其进行有序的控制和自动探测过程仍是目前研究的热门问题之一[3]。

支持向量机（Support Vector Machines，SVM）算法[4]一经提出就得到国内外专家学者的广泛关注，它被认为是继神经网络之后，一个新的数据处理研究方向，在很短的时间内取得了一系列令人瞩目的研究成果。在测量误差处理方面，基于SVM有大量理论研究成果涌现。例如Anthon 等人给出了关于硬邻域SVM学习误差的严格理论界限；Shawe-Taylor 和Cristianini 也给出了类似的关于软邻域SVM和回归情况下的误差界限。本文基于SVM算法原理设计了粗差定位与剔除模型，并将模型应用于某基坑沉降监测的实际工程中，通过实测数据，对模型进行了性能评价，验证了模型在粗差定位与剔除方面的可行性。

1 SVM 预测模型的构建

SVM 的基本思想是定义一个最佳线性超平面并找到最佳线性超平面，以减少求解凸规划问题的算法。无限维特征空间（希尔伯空间）。您可以通过高维特征空间中的线性超平面线性分割（或回归）在低维样本空间中无法进行线性处理的样本集。接下来，我们应用Mercer 核函数扩展定理来解决获取非线性映射方法的复杂性。这消除了知道非线性映射的显式表示的需要，但是线性学习机方法可以应用于高维特征空间。

支持向量回归的基本思想可以概括为：通过非线性映射函数将n 维输入数据映射到高维特征空间，并在该空间中执行线性回归。

2 模型应用- 以某基坑沉降检测工程为例

此实验中使用的工程示例是一个房地产项目，其中地面上的主要建筑物为25 层，讲台为5 至6 层，地下室为3 层，框架或框架剪力结构，建筑的基础是整体，建筑的基础。深度是海拔以下16.57m。由于工程规模大，开挖深，在基坑施工过程中，基坑内外的土由静态转变为被动和主动土压力，围护结构的变形超过允许范围。基坑变得不稳定并被破坏，并且对周围环境产生不利影响。了解基坑的变形，随着时间的推移发现建筑物的沉陷，并采取措施确保施工的顺利进行，安全使用建筑物，同时对未来进行合理设计，也为工程施工监控提供信息。

监控工作基于全部或部分原则。首先，建立集成的监控网络，然后基于它建立监控点。在整个过程中，总共设置了7 个监控点，并进行了30 次观察。

剔除第13 期和第18 期数据，建立SVM模型继续进行粗差剔除粉刺，并预测后10 期观测数据，如表1 所示。

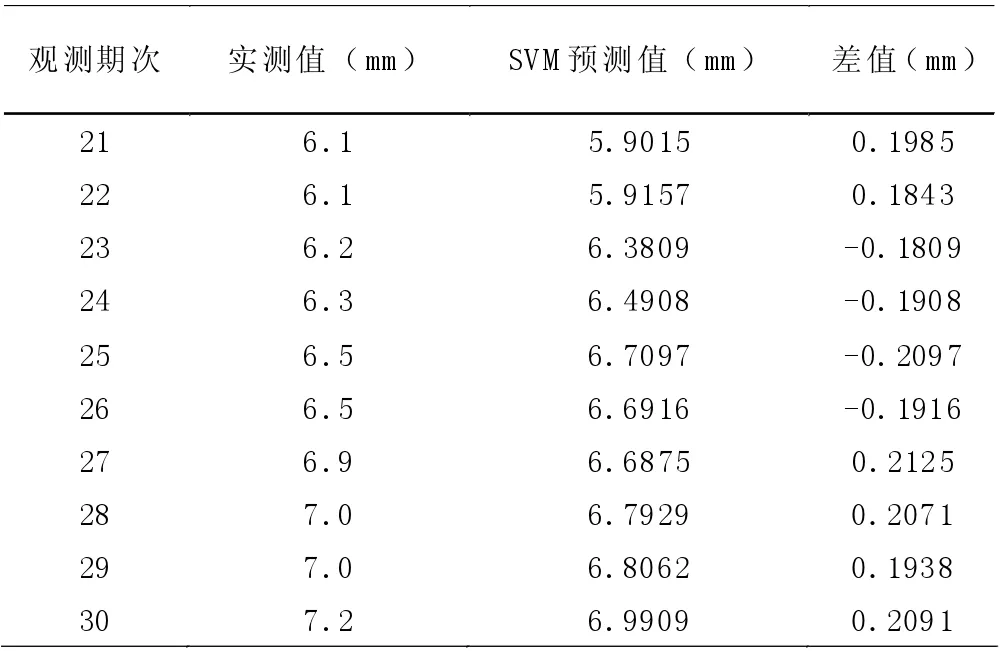
表1 粗差剔除后沉降量精度对比表

从表1 可以看出：经过剔除后建立的SVM模型与实测值比较，更加贴近实测值，效果比较理想；从表1 知经过剔除后建立的SVM模型所预测的后10 期数据，得到的SVM预测数据和实测值之间差值明显缩小，而且更加稳定，其中误差m=10.2088mm。

经过剔除前后的对比，可以得知：经过SVM 模型剔除的数据所预测的数据样本比没有剔除直接进行预测的数据样本精度更高，更加具有代表性。

3 模型性能评价

为了评价SVM预测模型的性能，利用多元回归模型实现粗差的剔除，并统计其剔除结果的精度，与SVM预测模型的性能进行对比，对比精度如图1 所示。

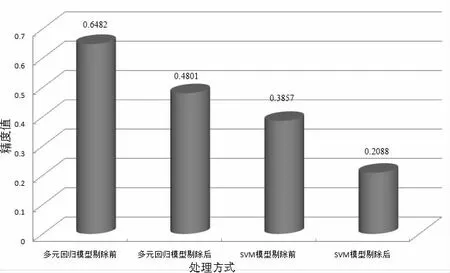
图1 精度对比图

两种方法在处理含有粗差的数据中都有较为明显的成果。多元回归模型与SVM模型均具有很好的抗粗差性，但从剔除效果来看SVM模型的剔除的效果更好，精度更高。

4 结论

本文提出了一种利用SVM预测模型，对测量粗差定位和剔除的方法。SVM理论具有可处理线性和非线性问题的能力，比较适用于测量粗差的定位和剔除。通过在某基坑沉降检测工程的实际应用，验证了SVM预测模型具有定位粗差和剔除粗差的实用价值。同时，通过与多元回归模型的对比实验，进一步证实了SVM预测模型具有较高的定位和粗差剔除精度，说明本文方法是针对粗差定位和剔除的有效方法。