钠冷快堆系统分析程序FR-Sdaso衰变热计算模型开发与验证

杨 军，贾鸿玉，杨晓燕，王晓坤

(中国原子能科学研究院 反应堆工程技术研究部，北京 102413)

反应堆长时间运行后停堆，裂变功率迅速下降，而堆芯衰变热则缓慢下降，堆芯余热在停堆初期由裂变功率和衰变热构成，停堆后期主要由衰变热构成。停堆余热根据产生方式主要分为以下几项：1) 裂变产物及裂变产物中子活化后的衰变热；2) 放射性锕系核素的衰变热；3) 缓发中子和自发裂变导致的残余裂变热；4) 结构材料中子活化后的衰变热[1]。虽然衰变热一般只占到反应堆额定功率的百分之几，但若不及时导出，将导致燃料元件因过热而烧毁，因此反应堆停闭时的余热导出是反应堆设计时需考虑的重要安全功能之一[2]。

系统分析程序是反应堆工况设计分析和事故分析的重要计算工具。目前国际上发展钠冷快堆的国家大都开发了快堆系统分析程序，如美国阿贡国家实验室(ANL)开发的SAS4A/SASSYS-1程序[3]、法国原子能委员会(CEA)开发的OASIS程序[4]、韩国原子能研究院(KAERI)开发的MARS-LMR程序[5]、西安交通大学开发的THACS程序[6]、华北电力大学开发的SAC-CFR程序[7]、哈尔滨工程大学开发的THPCS程序[8]等。

FR-Sdaso程序为中国原子能科学研究院针对大型池式钠冷快堆开发的系统瞬态分析程序，其计算范围涵盖钠冷快堆主热传输系统，可分析钠冷快堆电厂在正常运行工况及各类事故工况下的瞬态响应[9]，已用于示范快堆工况设计及安全分析。本文开发FR-Sdaso程序中所使用的衰变热计算模型，并对模型进行验证。

1 衰变热计算方法

停堆后衰变热的计算一般有两种方法[10-11]：累计方法和量热法。

累计方法单独处理堆内数百种裂变产物中的每一种裂变产物的衰变热，然后相加求得反应堆总的衰变热。该方法主要依赖于裂变产物数据的正确性，需要专用的计算软件，典型如美国橡树岭国家实验室编制的ORIGEN程序。累计方法的上述特点，导致其难以应用于系统分析程序。

量热法使用停堆后的衰变热积分实验曲线，进行指数多项式拟合，然后利用拟合公式计算。典型的量热法计算公式[12]如下：

Pd(τ,T)=4.1×1011P[τ-0.2-(τ+T)-0.2]

(1)

其中：Pd(τ,T)为停堆后的衰变热，MeV/s；P为停堆前的功率，W；τ为停堆后的时刻，s；T为停堆前维持功率P连续运行的时间，s。

一方面量热法只能单独计算衰变热，不能考虑瞬态过程中裂变功率对衰变热的影响，另一方面目前尚无成熟的针对钠冷快堆的量热法计算公式。因此，本文开发一种可用于钠冷快堆系统分析程序模拟衰变热的集总计算方法，可考虑裂变功率和功率历史对衰变热的影响。

1.1 衰变热计算模型

某种裂变产物或锕系核素的浓度可近似计算[12]如下：

(2)

其中：hj(t)为t时刻第j种裂变产物或锕系核素的浓度，m-3；γj为第j种裂变产物或锕系核素的产额；Σf为总裂变截面，m-1；φ(t)为t时刻中子通量密度，m-2·s-1；λj为第j种裂变产物或锕系核素的衰变常量，s-1。实际应用中可用式(2)近似模拟1组裂变产物或锕系核素浓度的变化。

在式(2)两边同乘以第j种裂变产物或锕系核素每次衰变释放出的能量Edj(J)，有：

(3)

令Edjhj(t)=Hj(t)，有：

(4)

对式(4)做如下变换：

(5)

其中：Ef为单次裂变释放的能量，J；EfΣfφ(t)=N(t)为裂变功率密度，W/m3。

令Edjγj/Ef=Ej为无量纲数，则式(5)变换为：

(6)

其中：裂变功率密度N(t)可由点堆模型计算；Ej为常数，表示各核素对应的功率份额；λjHj(t)为第j种裂变产物或锕系核素t时刻的衰变热密度。应用式(6)即可计算衰变热[13]。显然，瞬态过程中裂变功率将对衰变热产生影响。

1.2 初始条件确定

反应堆停堆后的衰变热受反应堆运行功率历史的影响，因此初始化过程需考虑不同功率历史对衰变热计算的影响。

假设某反应堆的功率历史可简化为图1所示的N段，每个分段内反应堆总功率为常数，分别为P1，P2，P3，…，PN，每个时间段的时刻分割点分别为T1，T2，T3，…，TN。

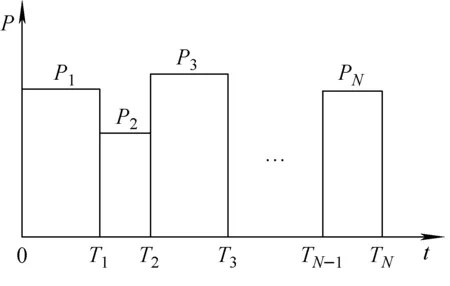
图1 反应堆功率历史示意图Fig.1 Diagram of reactor power history

对式(6)在时间0～TN内积分可得：

(7)

分别在图1所示的N个时间分段内考虑式(7)右端积分，可得：

exp[-λj(TN-T1)]+

exp[-λj(TN-Tn)]+NN+

(8)

其中：M为所考虑的裂变产物或锕系核素种类，系统程序处理中一般可将裂变产物或锕系核素根据其衰变常量的大小归并为若干组，此时M即表示组数；N1，N2，N3，…，NN分别为T1，T2，T3，…，TN时刻的裂变功率。根据式(8)可求得N1，N2，N3，…，NN，最终对于N段功率历史的情形，第j种核素的衰变热的初始值为：

λjHj(TN)=EjN1(1-e-λjT1)e-λj(TN-T1)+

e-λj(TN-Tn)+EjNN(1-e-λj(TN-TN-1))

(9)

总的衰变热Pd为各组产物衰变热之和：

(10)

最后，初始化过程中如果某一功率历史分段末尾已有的衰变热高于该时段的给定功率，则取该时段末尾裂变功率为0。例如，如果反应堆的功率历史中有一段时间处于零功率停堆状态，则初始化计算中该时间段末尾对应的裂变功率取值为0。

2 模型验证

模型验证分为两部分，第一部分选取ANSI/ANS-5.1—2005标准[14]中的数据，不考虑裂变功率影响，只计算停堆后的衰变热，验证不同功率历史下衰变热的计算；第二部分选取中国实验快堆(CEFR)的设计数据，考虑裂变功率的影响，验证衰变热的计算。

2.1 基于ANSI/ANS-5.1—2005标准的验证

美国核学会(ANS)衰变热计算标准(ANSI/ANS-5.1—2005)是ANS于2005年发布的针对轻水堆的衰变热计算标准，该标准给出了235U、238U、239Pu和241Pu等核素发生单次裂变及辐照足够长时间(1013s)后衰变热随时间的变化[14]，标准中给出的数据可用于验证所开发的模型。

1) 单一功率历史验证

考虑某一核素辐照足够长时间(1013s)后衰变热的变化，可近似等效为以该种核素为堆芯的反应堆以固定功率运行1013s后停堆，计算停堆后衰变热随时间的变化，功率历史如图2所示。

只有一段功率历史时，t时刻的衰变热为：

(11)

其中，N1为Top时刻的裂变功率，由下式计算：

(12)

计算时裂变产物分组参考标准划分为23组。每组产物对应的衰变常量λj、无量纲数Ej可由标准给出的数据求得。FR-Sdaso程序计算结果和ANS标准数据的比较列于表1、2，因标准中只给出了4位有效数字，所以程序计算结果也取4位有效数字。

表1 辐照1013 s后停堆FR-Sdaso计算和ANS标准的相对衰变热Table 1 Relative decay heat calculated by FR-Sdaso and in ANS standard after 1013 s irradiation shutdown

综上可见，所开发衰变热模型的计算结果与ANSI/ANS-5.1—2005标准结果相比，在所计算的时长范围内(0～109s)，采用科学计数法保留4位有效数字时，最大相对偏差约为0.1%，结果符合良好，初步证明了所开发模型的正确性。

2) 多段功率历史验证

SAS4A/SASYS-1程序[3]是美国阿贡国家实验室开发的钠冷快堆系统分析程序，该程序已经过较为充分的验证，广泛应用于钠冷快堆系统分析计算[15-16]。为进一步验证所开发模型对功率历史影响模拟的正确性，以ANSI/ANS-5.1—2005标准中衰变热计算采用的衰变常量λj和无量纲数Ej为输入条件，假设了一种反应堆功率历史，分别计算了235U、238U、239Pu和241Pu经历所假设的功率历史后衰变热的变化，并与SAS4A/SASYS-1的计算结果[17]进行比较。

假设功率历史如图3所示，划分为4段，反应堆首先满功率运行13周，停堆维持零功率1周，然后维持50%功率1周，最后维持满功率1 d后停堆，计算此后衰变热随时间的变化。4种核素的计算结果及偏差列于表3、4。可看出，FR-Sdaso和SAS4A/SASYS-1计算的最大相对偏差约为5.6×10-8，结果符合良好，初步证明了所开发模型的正确性。

表2 辐照1013 s后停堆FR-Sdaso与ANS标准相对衰变热的相对偏差Table 2 Relative deviation between FR-Sdaso and ANS after 1013 s irradiation shutdown

图3 多段功率历史示意图Fig.3 Schematic of multi period power history

表3 多段功率历史下FR-Sdaso和SAS4A/SASYS-1计算所得相对衰变热Table 3 Relative decay heat calculated by FR-Sdaso and SAS4A/SASYS-1 under multi period power history

表4 多段功率历史下FR-Sdaso与SAS4A/SASYS-1计算结果相对偏差Table 4 Relative deviation between FR-Sdaso and SAS4A/SASYS-1 results under multi period power history

2.2 CEFR停堆算例验证

CEFR停堆算例考虑裂变功率对衰变热的影响，采用CEFR的设计参数，分别采用FR-Sdaso和SAS4A/SASYS-1程序计算了CEFR紧急停堆过程中衰变热的变化，功率历史考虑反应堆满功率连续运行80 d后紧急停堆，主要的输入参数列于表5～7。

表5 CEFR停堆算例主要输入参数Table 5 Main input parameter of CEFR shutdown calculation case

表6 缓发中子的衰变常量和有效缓发中子份额Table 6 Decay constant and effective fraction of delayed neutron

为单独验证功率计算，不考虑反馈反应性，紧急停堆过程中控制棒引入的反应性采用式(13)模拟。

表7 各裂变产物或锕系核素的衰变常量和功率份额Table 7 Decay constant and power fraction of each group of fission product or actinide

(13)

其中：ρ(t)为紧急停堆后t时刻引入的反应性，pcm；t为紧急停堆后的时刻，s。

图4为FR-Sdaso和SAS4A/SASYS-1计算所得裂变功率和衰变热。可看出，FR-Sdaso和SAS4A/SASYS-1程序计算所得裂变功率的最大相对偏差在10-6量级，衰变热的最大相对偏差在10-8量级，结果符合良好。衰变热的最大相对偏差出现在紧急停堆初期，控制棒下插到底后，相对偏差出现波动，后续随着裂变功率和衰变热的衰减，相对偏差逐渐减小，计算结

图4 FR-Sdaso和SAS4A/SASYS-1计算所得裂变功率和衰变热Fig.4 Fission power and decay heat calculated by FR-Sdaso and SAS4A/SASYS-1

果初步证明了所开发模型的正确性。

3 裂变功率对衰变热的影响分析

为进一步分析裂变功率在紧急停堆瞬态过程中对衰变热的影响，采用FR-Sdaso计算了不考虑裂变功率影响时的衰变热，对比结果如图5所示。图中衰变热Y和衰变热N分别表示考虑和不考虑裂变功率影响的结果。紧急停堆过程中，裂变功率的衰减需要一定的时间，在此期间仍不断有裂变产物或锕系核素产生，因此考虑裂变功率对衰变热的影响后，计算所得的衰变热更高，两者的最大相对偏差(相对偏差=(衰变热N-衰变热Y)/衰变热Y)出现在停堆初期，约为-7%，出现最大偏差的时刻被低估的衰变热约为0.29 MW，后续随紧急停堆后裂变功率和衰变热的下降，相对偏差逐渐减小，约100 s后相对偏差下降至-1%以下。

图5 停堆初期裂变功率对衰变热的影响Fig.5 Influence of fission power on decay heat during initial shutdown

4 结论

本文开发了一种可用于钠冷快堆系统分析程序的衰变热计算模型，该模型可考虑裂变功率和功率历史对衰变热的影响。并通过与ANSI/ANS-5.1—2005标准和SAS4A/SASYS-1程序计算结果对比，初步验证了所开发模型的正确性。基于中国实验快堆的设计数据，分析了紧急停堆过程中裂变功率的变化对衰变热的影响，结果表明计算停堆初期衰变热时应考虑裂变功率的影响。

本模型的开发为自主化池式钠冷快堆系统分析程序FR-Sdaso提供了衰变热模型，后续将继续对模型进行分析和验证，为我国大型钠冷快堆的设计分析提供技术支持。