某汽车喇叭支架的断裂分析及改进设计

刘 庆，李 倩，陆志成

某汽车喇叭支架的断裂分析及改进设计

刘 庆1，李 倩1，陆志成2

（1.河南工学院 车辆与交通工程学院，河南 新乡 453003；2.神龙汽车有限公司 技术中心，湖北 武汉 430056）

针对振动耐久性试验中某车型喇叭系统支架发生的断裂失效问题，建立汽车喇叭支架系统的有限元分析模型，对喇叭支架进行了模态、频率响应及疲劳分析，分析了喇叭支架工作中产生断裂的原因,并提出了结构改进方案。仿真计算和试验结果均表明，新方案的设计满足喇叭支架系统的抗疲劳强度和疲劳寿命的要求，其改进设计方法对类似结构设计具有参考意义。

喇叭支架；振动疲劳；动应力

在实际工程中，许多结构在承受动态载荷（如振动、冲击、噪声载荷等）时会产生不同的振动响应，虽然这种动态载荷一般远小于静态载荷下的结构强度极限，但在其反复作用下，结构会产生裂纹并导致突然断裂，从而造成严重后果，这种现象被称为振动疲劳破坏[1-4]。

振动疲劳是指结构的疲劳破坏与结构的振动响应（包括结构固有频率、交变载荷变化频率、振动幅值、振动相位和结构的振型等模态）密切相关的失效现象。与主要考虑结构设计上应力应变分布的静态疲劳不同，振动疲劳将静态疲劳和结构动力学相结合，着重考虑结构的动力学响应[5-7]。

本文试以因振动疲劳而造成的某车型喇叭支架断裂问题为例，将有限元振动疲劳分析方法和试验方法相结合，验证有限元仿真模型的正确性，据此在原模型的基础上通过加强断裂位置局部结构的刚度对其进行改进设计，并顺利通过试验验证。

1 喇叭支架的断裂分析

在汽车行驶过程中，喇叭系统因承受来自外部的各种动态载荷（如位移激励、加速度激励）而产生振动响应。通过耐久台架试验，可以预测该系统结构中的薄弱环节，即容易产生断裂的部位，进而改进设计。测试的扫频范围为20～250Hz，在不同的频率段内，加速度激励大小不同，如表1所示。喇叭支架的断裂情况如图1所示。

表1 振动试验要求

图1 喇叭支架断裂件

试验测得喇叭支架系统的共振频率为23.98Hz，该频率落在20～27Hz频段中，此时的激励为4g，激励最大。该喇叭支架的断裂是由加速度激励引起局部模态与载荷的振动耦合造成的，属于支架的振动疲劳失效，可以借助有限元振动疲劳分析方法来分析该喇叭支架的断裂问题，并找到改进方案。

2 有限元模型的建立

汽车喇叭系统由喇叭支架、喇叭本体及喇叭避震片（两个1mm的避震片）组成，避震片与喇叭支架和喇叭本体均通过一个M8的螺栓连接，喇叭支架通过一个M8的螺栓固定在汽车前纵梁上，并通过纵梁定位槽定位，如图2所示。

图2 喇叭支架的三维模型

该汽车喇叭系统中，喇叭本体的质量为0.2kg，在有限元模型中用集中质量进行模拟，通过RBE3单元与避震片连接，避震片及支架和喇叭本体及支架与纵梁之间采用RBE2单元共节点连接方式，由于质量会影响喇叭总成的模态，在模型中也应考虑连接避震片与支架的螺栓质量，通过集中质量进行模拟。

根据以上思路，借助HyperMesh软件建立该汽车喇叭系统的有限元模型，并定义相应的材料特性和边界条件，如图3所示。喇叭支架的材料牌号为DC01，屈服应力为216MPa，拉伸极限为345MPa，疲劳极限为115MPa，剪切模量为90,000 MPa[8]，避震片的材料为65Mn；边界条件为安装喇叭支架的钣金件截面全约束。

图3 喇叭支架的有限元网格模型

3 喇叭支架的有限元仿真分析

3.1 结构阻尼的确定

阻尼是结构抗振分析中的一个重要因素，对系统的响应有较大的影响，是结构动力分析的基本参数。目前，动力学分析采用的阻尼类型有结构阻尼与粘滞阻尼。结构阻尼是假设结构振动时, 阻尼力与单元力成正比,方向与单元变形率方向相反；粘滞阻尼是假定阻尼力与质点的运动速度成正比。实际结构分析中，主要采用粘滞阻尼理论。

为了确定阻尼的大小，首先将CAE仿真与试验进行加速度响应对标，测量点为支架与避震片连接处，试验测得该处的加速度值为313,980mm/s2。通过大量的对标，最终选取全局结构阻尼=0.06。喇叭系统有一个避震片，具有很好的弹性，避震片的单元阻尼定义为e=0.04。最后仿真得到支架与避震片连接处的加速度为314,359mm/s2，与试验结果吻合较好。加速度响应曲线如图4所示。

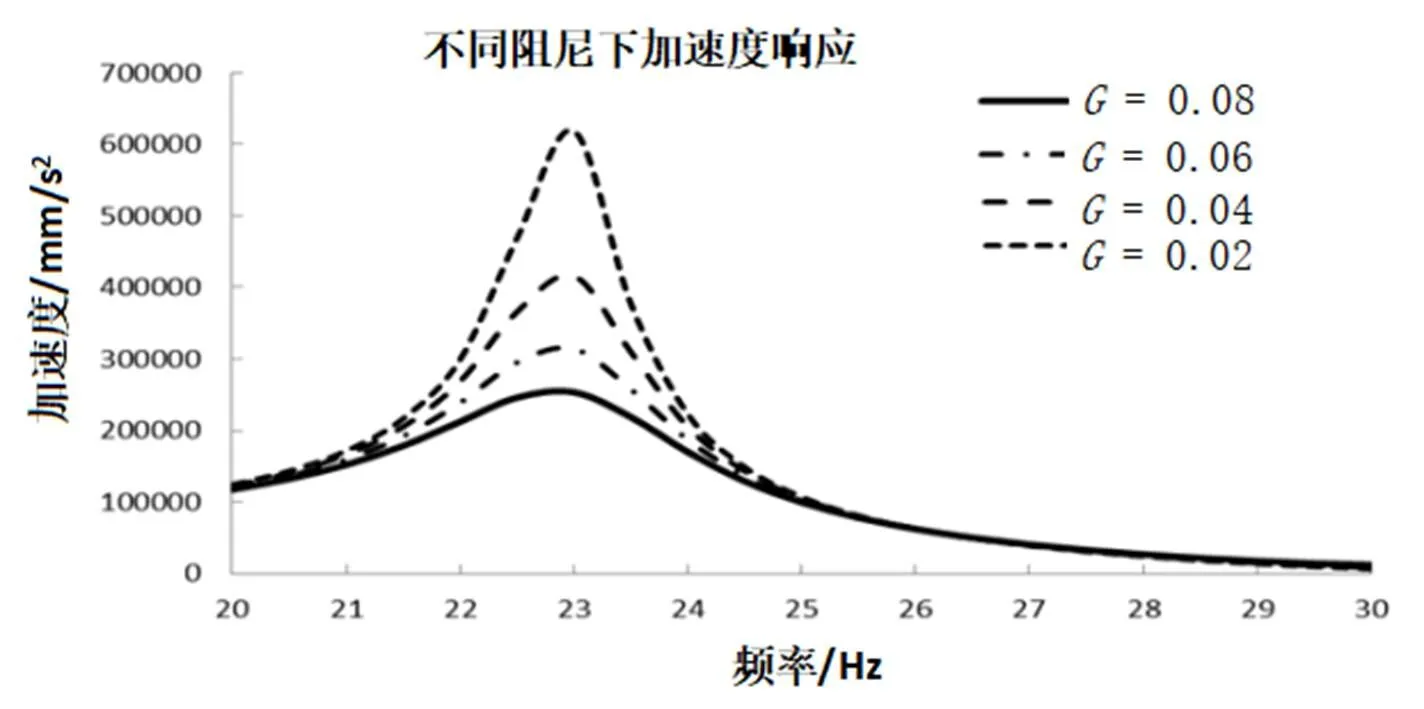
图4 加速度响应曲线

3.2 有限元模型的模态分析

利用专业的线性分析软件Nastran对有限元模型进行模态分析，确定其第一阶振动模态。仿真中第一阶模态频率为24.28Hz，方向为方向，试验测得在试验台架上的向振动频率第一个峰值为24Hz，仿真值与试验值相吻合，验证了建模方法及阻尼定义的合理性。仿真及试验的模态结果如图5所示。

图5 喇叭支架模态结果

3.3 有限元模型的频率响应分析

利用Nastran软件求解器，基于试验的边界在20～27Hz的频率范围内，在三个方向上用4g的加速度激励分别进行频率响应分析，全局结构阻尼大小为0.06，避震片单元阻尼为0.1，计算出每个方向的动应力值，结果如表2所示，应力位置如图6所示，方向上应力最大值均出现在24Hz，向的应力值最大，出现在倒角区域，与试验破坏的位置相符，进一步验证了建模的合理性。

表2 喇叭支架在24Hz/4g加速度下激励的结果

图6 喇叭支架在24Hz/4g加速度下激励的动应力云图

4 喇叭支架的改进设计

4.1 改进方案的描述

解决该支架断裂问题的关键是降低喇叭支架折边过渡区域的应力，通常可以采用的方法主要有[9-10]：（1）使用更高强度的材料；（2）对弱区进行加强，降低局部应力值；（3）改变支架结构，例如可将支架折弯区域与根部距离加长、宽度尺寸加大。

本文采用第二种方法，在喇叭支架与车身固定的区域加一个厚度为2mm的加强板，尺寸及材料与原喇叭支架结构底部保持一致，通过加强根部的刚度来提高支架的模态频率，使模态频率达到27～100Hz之间，将振动激励载荷降到1.5g，从而减小共振时动应力值，最终优化方案如图7所示。

图7 喇叭支架改进后的方案

4.2 改进方案的有限元分析

对改进后的模型进行模态分析，从模态结果可知，第一阶模态频率从24.28Hz提高为28.09Hz，模态振型仍为系统的向弯曲振动，试验测得的频率为28.2Hz，与仿真结果相吻合，结果如图8所示。

对改进后的模型进行扫频步长为0.5Hz的频率响应分析，在共振频段区域，该方案的共振频率（带支架与避振片）为28.09Hz，在27～100Hz范围内，此时的激励为1.5g，在、、三方向上分别进行频率响应分析，计算出此时的动应力值，结果发现、、三个方向上的动应力最大值均出现在28Hz，应力最大值在圆孔区域，折弯区域应力较小，如图9所示。改进前后支架耐久振动强度比较如表3所示。

图8 改进后喇叭支架模态结果

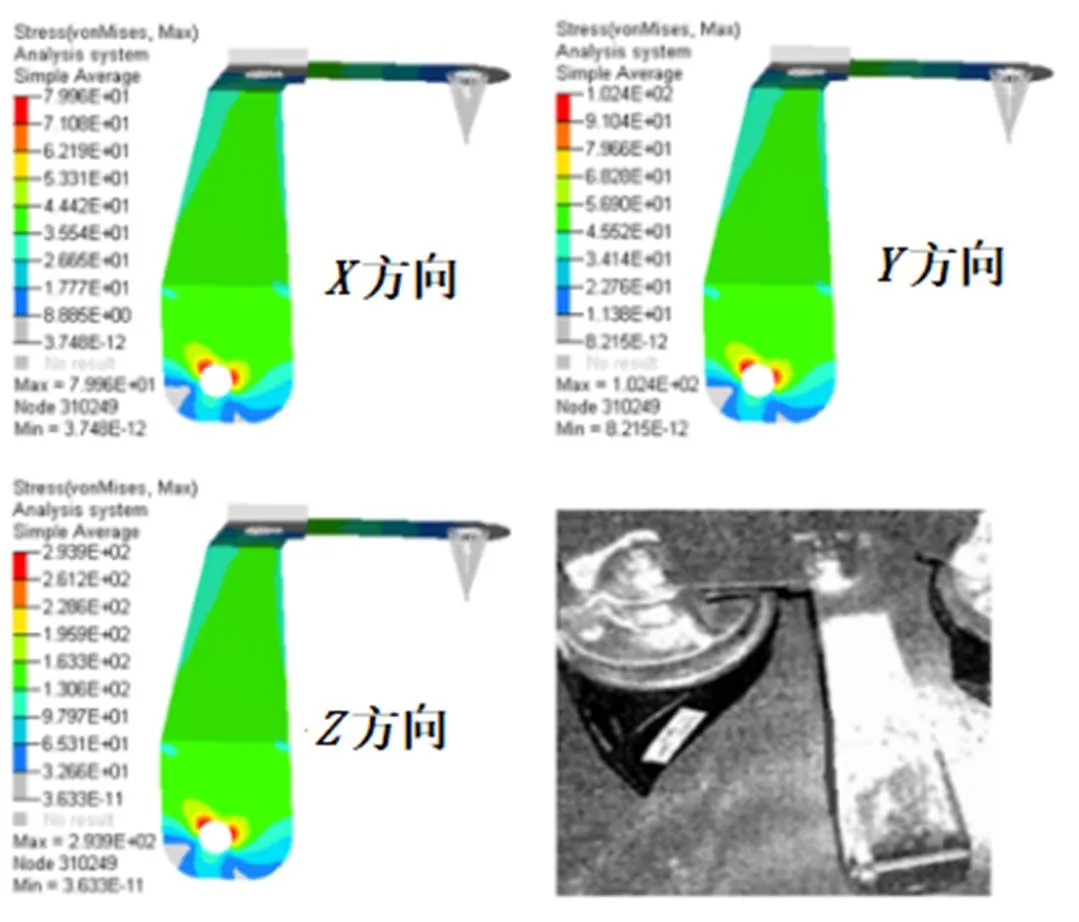
图9 改进后方案喇叭支架应力云图

表3 改进前后支架耐久振动强度比较

低周疲劳校核：低周疲劳破坏的极限应力可以利用Neuber应力计算公式（1）确定，得出其应力标准值为404MPa。仿真结果中，向动应力最大值为293.9MPa，远小于Neuber应力值，因此，改进方案不会出现低周疲劳问题。

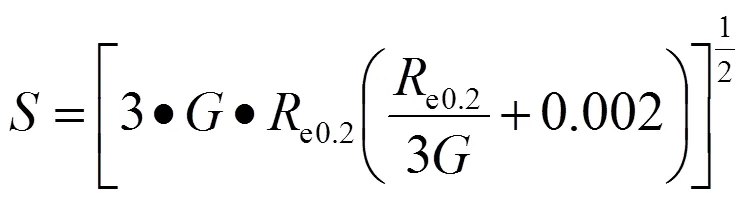
式中，为剪切模量，=90,000 MPa；e0.2为支架材料的屈服强度，e0.2=216MPa。

高周疲劳校核(疲劳寿命计算)：根据-疲劳寿命计算公式（2），计算出喇叭系统承受向最大应力下的寿命为=1.1×106，接近无限寿命，因此，改进方案不存在高周疲劳问题。

式中，为交变应力值，即扫频段的仿真动态应力值，=293.9MPa；e为材料的疲劳极限，e=115MPa；为斜率，=9。

4.3 改进方案的试验验证

针对改进方案，进行振动疲劳试验验证。根据实验要求，在三个方向上进行扫频试验。试验完成后，新方案下支架没有破坏，也没有产生裂纹，试验通过。

5 结语

本文对喇叭支架系统的断裂原因进行了分析，发现支架的局部振动模态与载荷的振动产生了耦合，造成支架的振动疲劳破坏。有限元振动疲劳分析和试验结果表明，加强断裂点局部结构的刚度可以降低振动激励载荷，从而减小共振时的动应力值，新方案的设计满足了喇叭支架系统的抗疲劳强度和疲劳寿命要求。同时，仿真人员可以借鉴本次改进思路进行相关结构优化分析。

[1] 姚卫星.结构疲劳寿命分析[M].北京:国防工业出版社,2003．

[2] 刘文光,陈国平,贺红林,等.结构振动疲劳研究综述[J].工程设计学报，2012,19(1):1-8.

[3] 姚起杭,姚军.工程结构的振动疲劳问题[J].应用力学学报,2006,23(1):12-17.

[4] DAMIR A N, ELKHATIB A, NASSEF G. Prediction of fatigue life using modal analysis for grey and ductile cast iron[J]. International jouranl of fatigue, 2007,29(26): 499-507.

[5] 孙伟.结构振动疲劳寿命估算方法研究[D].南京:南京航空航天大学，2005.

[6] 何锋,冯春亮.汽车挡风玻璃洗涤液喷水壶模态与频响分析[J].汽车零部件，2013(11):54-56.

[7] 张庆军,王晓琳.基于频率响应的客车骨架结构优化[J].汽车工程师，2014(10):23-25.

[8] 陆明炯.实用机械工程材料手册[M].沈阳:辽宁科学技术出版社，2002．

[9] 王建平,赵冬冬,史文涛,等.基于有限元计算的泥浆泵泵体结构改进分析[J].河南理工大学学报(自然科学版), 2013,32(5):576-579.

[10] 彭海军,张磊,张彤.某型设备支架故障分析与改进设计[J].四川兵工学报，2011,32(3):98-111.

Fracture Analysis and Improved Design of Vehicle Horn Bracket

LIU Qing1，LI Qian1，LU Zhi-cheng2

(1.College of Vehicle and Transportation Engineering, Henan Institute of Technology, Xinxiang 453003, China; 2.Technology Center, Dongfeng Peugeot Citroen Automobile Company Ltd, Wuhan 430056, China)

For the fracture failure problem of vehicle horn bracket in vibration failure test, The finite element analysis model of vehicle horn bracket system is established. The modal analysis, frequency response analysis, failure analysis of the model is conducted and the fracture reasons of horn bracket are obtained. Then we can get the improved design by adjusting local structure of horn bracket. The analysis and test results show that the new design meets horn bracket’s requirements of fatigue strength and fatigue life. Research methods of this paper can be a reference value in similar structure optimization design．

horn bracket; vibration fatigue; dynamic stress

TH463

A

2096–7772(2020)03–0019–05

2020-03-06

刘庆（1983―），男，河南新乡人，讲师，硕士，主要从事机械设计及制造、汽车CAD/CAE研究。

（责任编辑吕春红）